|
|
 |
 |

|
| |
АССОЦИАТИВНОЕ ЗУ С ИСПОЛЬЗОВАНИЕМ РЕШЕТЧАТЫХ СТРУКТУР
Ф.М.Шавердян
Рассматриваются вопросы представления информации в ассоциативном ЗУ с помощью полученного на основе решетчатых структур набора символов с контролируемым спектральным разделением. Приводятся схемная реализация такого ЗУ, расчетные и экспериментальные данные.
Введение
Особенности когерентно-оптических систем позволяют использовать их для создания ассоциативных ЗУ (АЗУ), в основе принципа действия которых лежат метода преобразования Фурье и фильтрации в спектральной плоскости.
Основное требование, предъявляемое к набору символов, используемому для кодирования слов в таком АЗУ, состоит в том, что спектры символов должны иметь незначительное взаимное перекрытие с целью создания предпосылок для проведения эффективной фильтрации в спектральной плоскости. Наиболее привлекательными о этой точки зрения являются решетчатые структуры /1/.
Общее описание АЗУ
На рис.1 приведена оптическая схема АЗУ. В объективной плоскости Р 1 находится матрица памяти с множеством слов, над которым производится операция ассоциативного поиска. Запрос, соответствующий некоторому слову, вводится в АЗУ путем помещения в спектральную плоскость Р2 соответствующего фильтра. Плоскость Р3 является плоскостью восстановления по отфильтрованному спектру. Анализируя конфигурации восстановленных символов в совокупностях
- 326 -
позиций, относящихся к отдельным словам, можно на основе критериев формального соответствия выявить релевантные слова.
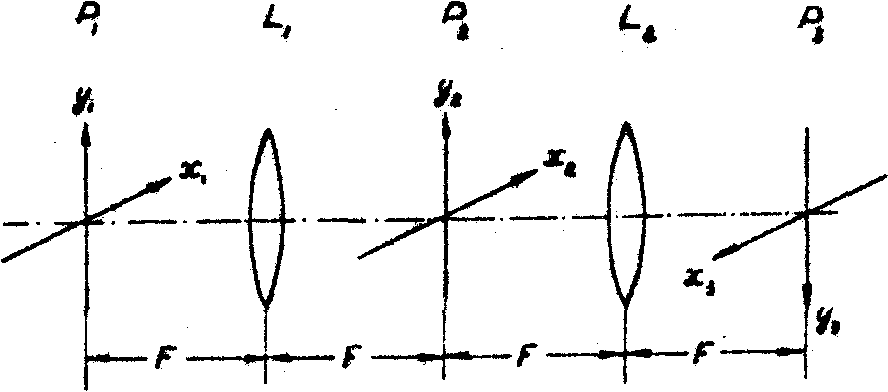
Рис.1 . Оптическая схема АЗУ (l1, l2 - линзы, выполняющие преобразование Фурье, f - фокусное расстояние линз).
Слова АЗУ могут являться поисковыми признаками слов, хранящихся в некотором постоянном адресном ЗУ, и в атом случав позициям слов в плоскости Р 3 могут быть поставлены в соответствие адреса этого постоянного адресного ЗУ.
Описание используемого иабора символов
В качестве функция, описывающей отдельный символ, рассмотрим функцию
s(x,y) = q(x,y)·p(x,y) (1)
где p(x,у) представляет собой некоторую апертурную функцию, стандартную дня всех символов.
В качестве q(x,у) возьмем функцию, описывающую синусоидальную решетку, полосы которой наклонены по отношению х оси у на угол j
:
q(x,y) = a + bcos[2p
w
(xcosj
+ ysinj
)]
- 327 - •
где а , Ь - некоторые постоянные, w
- пространственная частота решетки.
Взяв преобразование Фурье от (1), получим
|
s(¦
x,¦
y)=ap(¦
x,¦
y)+(b/2)·p(¦
x-w
cosj
,¦
y-w
sinj
)+ |
(2) |
|
+(b/2)·p(¦
x + w
cosj
,¦
y + w
sinj
) |
где
s(¦ x,¦
y) =  [s(x,y)], p(¦
x.¦ y) = [s(x,y)], p(¦
x.¦ y) =  [p(x,y)] [p(x,y)]
Из (2) видно, что спектр функция s(x,у) представляет собой суперпозицию трех спектров апертурной функции, один аз которых находится в центре спектральной плоскости, а два других диаметрально разнесены в направлении, нормальном направлений полой исходной решетки. Меняя с определенным шагом частоту и ориентацию решетки, в спектральной плоскости мы получим множество различным образом разнесенных и ориентированных пар спектров апертурной функции. Каждой такой паре спектров сопутствует один несмещенный спектр, локализация которого является общей для всех пар спектров, поэтому его использование нецелесообразно, и он непременно маскируется. Таким образом, каждой паре разнесенных спектров на входной плоскости можно поставить в соответствие символ - апертурную функцию о соответствующими значениями пары "частота - ориентация" решетки. Выбором шага изменения частоты и ориентации можно управлять степенью разделения соседних пар спектров.
Исследование АЗУ для случая круглой стандартной апертуры
Круглая стандартная апертура радиуса r1 может быть представлена в виде функции
circ(r/r1) (3)
- 328 -
Рабочую область входной плоскости Р 1 возьмем в виде круга радиуса r1. Рабочую область спектральной плоскости возьмем в виде кольца, внутренний радиус которого обозначим через r2min, а внешний - через r2max.
При гексагональной упаковке символов (рис.5а) для количества символов, размещающихся в рабочей области входной плоскости, можем написать:
|
n1 = |
p
r21 |
|
2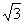 r21 r21
|
Спектр стандартной апертуры, описываемой выражением (3),имеет вид
r1j1(r12p
r
)/r
(4)
где j1 - функция Бесселя первого рода первого порядка,
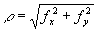
В координатах спектральной плоскости Р2 (4) будет представлено в виде амплитудного распределения, пропорционального величине
r1j1(r12p
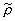 /l
f)/ /l
f)/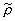 (5) (5)
где l
- длина волны используемого излучения,
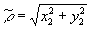
Из (5)
для значений 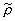 ,
при которых амплитуда спектра становится равной нулю, получаем ,
при которых амплитуда спектра становится равной нулю, получаем
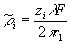 , i = 1,2,3,... (6) , i = 1,2,3,... (6)
где zi - корни уравнения j1(z)=0.
Поместив в спектральную плоскость фильтр, представляющих собой непрозрачный экран с двумя диаметрально разнесенными круглыми
- 329 -
отверстиями радиуса 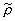 i
(где i
(где 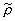 i
вычислено по (6)
для некоторого конкретного значения i),
пропускающими только центральные области некоторой пары разнесенных спектров,
можно в плоскости Р3
восстановить изображения только тех символов, которые соответствуют данной паре
разнесенных спектров. При этом количественной характеристикой пропускаемой части
спектра а, следовательно, и качества восстановления может служить значений числа
i, соответствующее номеру кольца спектра с
нулевым значением амплитуды, по которому производится срезание. i
вычислено по (6)
для некоторого конкретного значения i),
пропускающими только центральные области некоторой пары разнесенных спектров,
можно в плоскости Р3
восстановить изображения только тех символов, которые соответствуют данной паре
разнесенных спектров. При этом количественной характеристикой пропускаемой части
спектра а, следовательно, и качества восстановления может служить значений числа
i, соответствующее номеру кольца спектра с
нулевым значением амплитуды, по которому производится срезание.
Считая, что частота и ориентации у символов, используемых в
объектной плоскости таковы, что множество соответствующих им пар отверстий радиуса
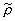 i
фильтра размещается в спектральной плоскости концентрическими слоями ширины
2 i
фильтра размещается в спектральной плоскости концентрическими слоями ширины
2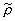 i
(рис.2), для количества символов в наборе получим i
(рис.2), для количества символов в наборе получим
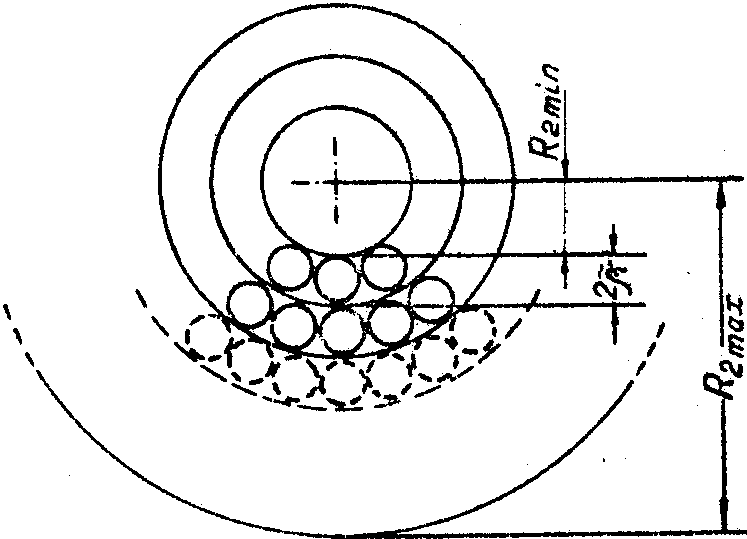
Рис.2. Размещение множества пар отверстий фильтра в спектральной плоскости.
- 330 -
Для того, чтобы фрагмент синусоидальной решетки, вырезаемый стандартной апертурой, проявил бы свою периодичность, необходимо, чтобы в нем находилось количество периодов решетки, не меньшее некоторого числа q. Отсюда для минимально допустимой частоты решетки можем написать
w
min ³
q/2r1 (7)
Для допустимого значения радиуса 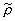 ц,
на котором находятся центры разнесенных спектров первого слоя, получим: ц,
на котором находятся центры разнесенных спектров первого слоя, получим:
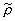
ц(w
min) ³ ql
А/2r1 (8)
Используя равенство
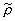
ц
= 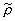 i + r2min i + r2min
а также (6), определим допустимое значение r2min с учетом ограничивающего влияния со стороны q:
|
r2min ³
|
ql
f |
- |
zil
f |
|
2r1 |
2p
r1 |
При определении допустимого значения r2min учитывается .также ограничивающее влияние маски, убирающей несмещенный спектр:
r2min = 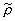 j j
где j - индекс, соответствующий номеру кольца спектра с нулевым значением амплитуды, по которому производится срезание маской.
Максимально допустимое значение частоты синусоидальной решетки определяется с учетом ограничивающего влияния двух факторов -- разрешающей способности материала матрицы памяти и величины r2max.
На рис.3 приведен график зависимости емкостей входной плоскости (n1) и спектральной плоскости (n2) от радиуса r1
- 331 -
апертуры символа.
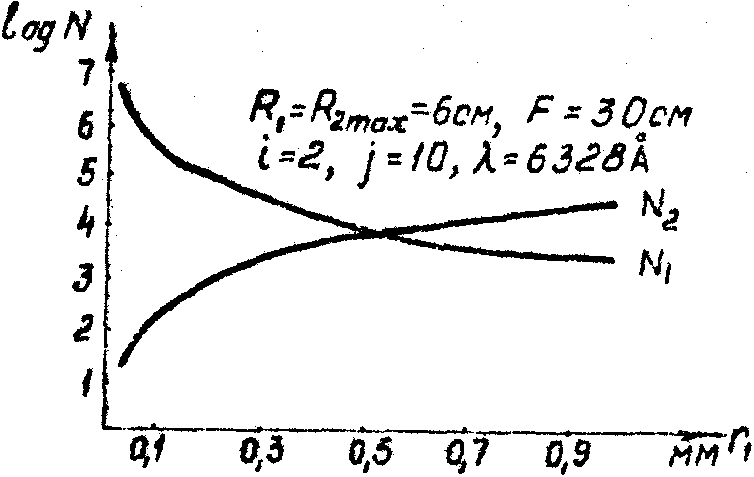
Рис.3. График зависимости емкостей входной плоскости (n1) и спектральной плоскости (n2) от радиуса r1 апертуры символа.
Возможность снижения требований, предъявляемых к качеству синусоидальных решеток
Максимальное значение используемой частоты, определенное в соответствия с изложенным в предыдущем разделе, обозначим через w
max. Легко заметить, что если w
min будет удовлетворять условию
w
min > w
max/2
то гармоники, которые могут возникнуть в результате несовершенства синусоидальной решетки, будут выходить за пределы рабочей области спектральной плоскости. АЗУ, использующее набор символов, созданный с учетом этого принципа, оказывается настолько некритичным к качеству решетчатой структуры, что становится допустимым, дало использование решеток Рончи. Возникающая при этом потеря емкости n2 не превышает 25%.
- 332 -
Кодирование словив АЗУ
Матрица памяти заполняется словами, представляющими собой последовательности из n символов. Будем трактовать олово как n-разрядный код с некоторым основанием С.
Инвариантность амплитудного спектра к сдвигу символов во входной плоскости делает невозможным использование одного и того же символа в различных разрядах кода, так как это приводит к вырождению слов. С целью снятия вырождения имеющийся набор символов разбивается на n групп и каждая такая группа привязывается к определенному разряду; для кодирования каждого разряда используются символы только соответствующей группы. Значение основания определяется при этом выражением
c = n2/n
Обозначив мощность кода через n2, получим:
n2 = (n2/n)n
Для емкости входной плоскости, выраженной в количестве кодов длины n, можем написать:
n1 = n1/n
Эксперимент
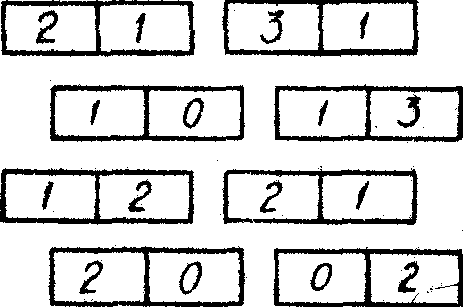
Был проведен эксперимент на физической модели. Массив слов, приведенный на рис.4а, в соответствии с таблицей кодирования (рис.4б) был представлен в виде матрицы памяти АЗУ (рис.5а). На рис.5б показан спектр этой матрицы. Далее показан результат восстановления исходной матрицы (рис.6а) при использовании фильтра, соответствующего пропусканию слова "21" (рис.6б).
Релевантным словам на рис.6а соответствуют конфигурации из двух восстановленных символов, соответственно количеству символов в слове; нерелевантным же словам соответствует количество
- 333 -
восстановленных символов меньше двух.
|
|
Значение разряда |
"0" |
"1" |
"2" |
"3" |
|
Номер разряда |
|
|
|
|
|
i |
|
|
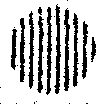
|
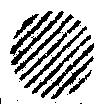
|
|
ii |

|
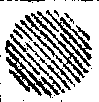
|
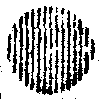
|
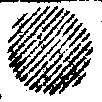
|
|
а) |
б) |
Рис. 4. Кодируемый массив слов (а) и таблица кодирования (б).
 
а) б)
Рис.5. Матрица памяти (а) и ее спектр (б).
С точки зрения технического удобства выявления релевантных слов интерес представляет схема, в которой релевантным словам соответствует отсутствие восстановления символов во всех разрядах слова. Такая схема реализуется при использовании фильтра, пропускающего все пары спектров, кроме пар, соответствующих запрашиваемому слову.
Нетрудно заметить, что работоспособность устройства полностью сохранится при использовании только одного из каждой пары
- 334 -
разнесенных спектров, различив будет состоять лишь в исчезновения у восстановленных символов решетчатой структуры двойной частоты.
 
а) б)
Рис. 6. Результат восстановления исходной матрицы (а) при использовании фильтра, соответствующего пропусканию слова "21" (б).
Заключение
Проведенное выше рассмотрение является попыткой показать принципиальную возможность создания АЗУ, использующих решетчатые структуры. Возможности практической реализации подобных АЗУ будут расширяться по мере прогресса в области технологии компонентов оптических вычислительных устройств.
Литература
1. p.u.will, k.s.pennington. "grid coding: a novel technique for Image processing", proc.ieee, v.60, pp.669-680, 1972.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

