|
|
 |
 |

|
| |
ИНВАРИАНТНОСТЬ К ПОВОРОТУ И МАСШТАБУ ПРИ КОМПЛЕКСНО-СОПРЯЖЕННОЙ ФИЛЬТРАЦИИ
Э.Г.Аветисов
Описан метод преобразования объектов, который в схемах согласованной фильтрации позволяет осуществить инвариантность к повороту в реальном масштабе времени, Метод основан на включении в оптическую систему фильтрации двухполостного оборачивающего конуса, обеспечивающего преобразование вращения мультипликации входного объекта. Приведены результаты эксперимента.
Метод распознавания образов на основе оптической согласованной фильтрации /1/ обладает рядом недостатков. Наиболее существенными из них являются чувствительность согласованных фильтров к повороту образов и к изменении их масштаба на входе системы распознавания. При изменении угловой ориентации или масштаба образа на входе системы величина отклика согласованного фильтра уменьшается, что приводит к снижению надежности процесса распознавания.
Инвариантность к повороту а к изменению масштаба при согласованной фильтрации обычно достигается посредством механического поиска /2/. Недостатками этого метода являются его трудоемкость и невозможность идентификации образов в реальном масштабе времени.
Предлагаемый в настоящей работе метод преобразования вращения образов в сочетании с согласованной фильтрацией позволяет реализацию оптического устройства распознавания образов параллельного действия, инвариантного к повороту. Благодаря параллельности действия устройства, обусловленной простотой
- 288 -
осуществления операции мультиплицирования в когерентных оптических системах /3/, становится возможным; распознавание образов в реальном масштабе времени. В таком устройстве должна выполняться операция дискретного мультиплицирования изображения эталонного образа ¦
(х,у), преобразование вращения мультипликации - поворот каждой К-той позиции мультипликации ¦
(х-ак,y-bк) на величину дискретизации a
пр относительно (К-1)-ой позиции. Мультиплицированный эталонный образ
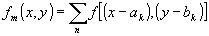 (1) (1)
подвергнутый преобразованию вращения, принимает вид
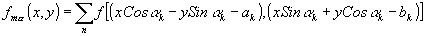 (2) (2)
где a
к = a
np·k, a
пр - предельный угол поворота, определяемый в результате анализа сигнального отклика системы оптической согласованной фильтрации. Далее этот преобразованный образ может быть задействовав в одной из схем согласованной фильтрации, позволяющей осуществить распознавание в реальной, масштабе времени (спектральный анализ интерференционной картины в выходной плоскости устройства согласованной фильтрации может проводиться либо с помощью электронного анализатора /4/, либо с помощью' движущейся решетки переменного периода /5/.
Рассмотрим оптическую схему фильтрации, а. которой спектральный анализ проводится чисто оптическим путем /6/. Этот способ, хотя и предусматривает двухступенчатый фотографический процесс, однако существенного различия в процесс распознавания не вносит и позволяет проще осуществить качественный анализ фильтрации с точки зрения преобразований в оптике.
В передней фокальной плоскости линзы (рис.1) расположены сформированное изображение преобразованной мультипликации эталонного образа ¦
ma
(х,у) и распределение сигнального объекта
- 289 -
q (х,у). дифракционная картина в задней фокальной плоскости описывается уравнением:
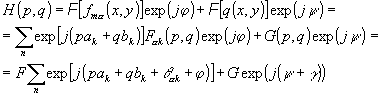 (3) (3)
где j
= 2p
(cp+dq)/l
f и y
= 2p
(sp+tq)/l
¦
- линейные фазовые набеги, характеризующие смещение преобразованной мультипликации и сигнального объекта относительно оптической оси, соответственно, q
a
k и g
характеризуют фазовые распределения спектров fa
k и g, соответственно.
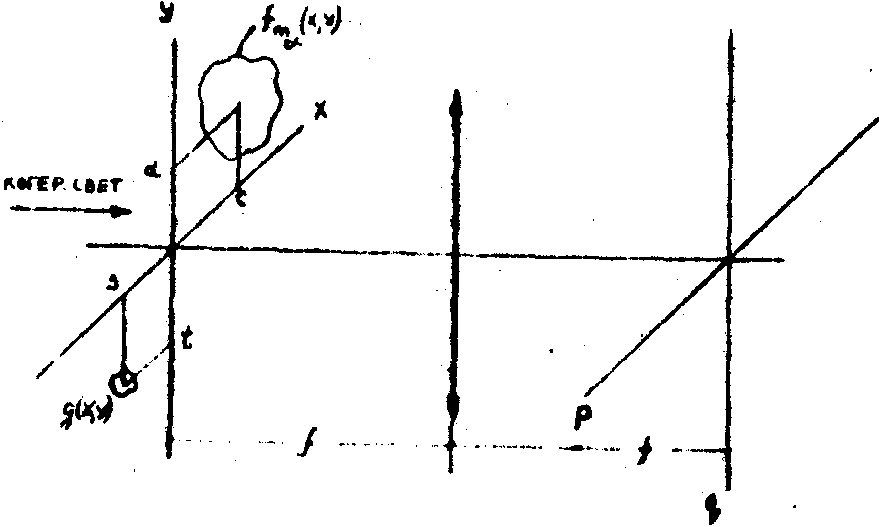
Рис.1. Схема получения интерференционной картины в Фурье-плоскости когерентного оптического анализатора спектра.
- 290 -
Фотопленка, помещенная в задней фокальной плоскости, зарегистрирует интенсивность суммарного распределения:
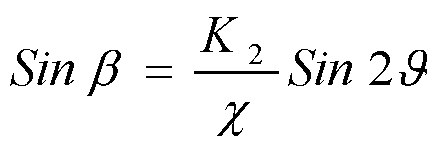 (4) (4)
Для получения функции взаимной корреляции распределений ¦
ma
(х,y) и q(x,у) необходимо осуществить пространственно-частотный спектральный анализ распределения интенсивности, зарегистрированной на фотопленке. Спектральный анализ проводится с помощью когерентного оптического анализатора спектра. В передней фокальной плоскости линзы (рис.2) размещается фотопленка с записью суммарного распределения интенсивности.
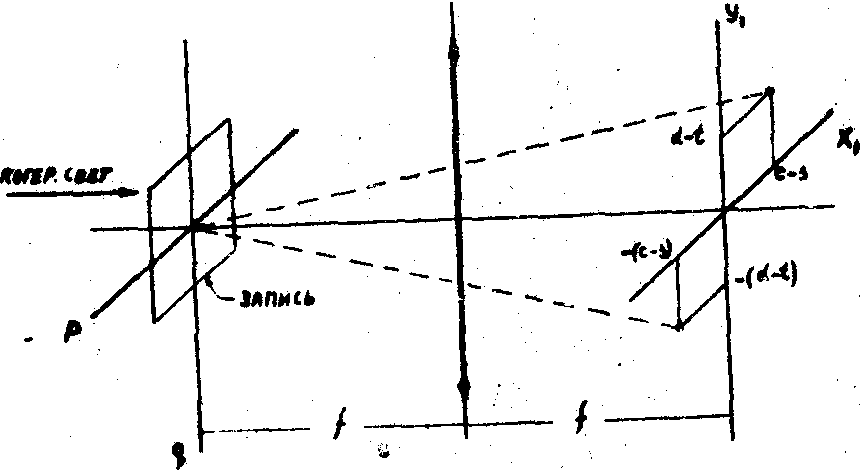
Рис.2. Схема спектрального анализа.
- 291 -
При освещении пленки плоской волной когерентного света в задней
фокальной плоскости получим преобразование Фурье этого распределения 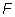 {|
h(p,q)| 2}. {|
h(p,q)| 2}.
Преобразование Фурье первого члена уравнения (4) представляет собой постоянную составляющую распределения в Фурье-плоскости анализатора спектра. Третий член уравнения (4) вносит вклад в распределение в виде суммы кросс-корреляционных составляющих, обусловленных перекрестной корреляцией между элементами мультипликации ¦
ma
(x,y). Интерес представляет преобразование Фурье интерференционного (второго) члена уравнения (4):
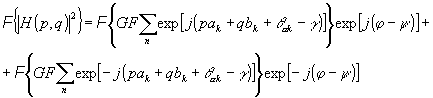 (5) (5)
Если
|
¦
(x,y)|
= |
q(x,y)|
q
ma
= g
(6)
где m определяет одну из позиций мультипликации, то уравнение (5) может быть выражено
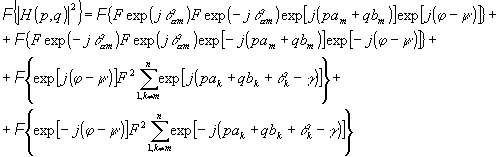 (5) (5)
В уравнении (7) первый член представляет собой автокорреляционную
- 292 -
функцию от ¦
(х,у), промодулированную фазовыми множителями exp[j(pam+qbm)] и exp[j(j
-y
)], обеспечивающими пространственное разделение.
Второй член-величина, комплексно-сопряженная с функцией, описываемой первым членом. Третий и четвертый члены – комплексно-сопряженные совокупности кросс-корреляционных функций, обусловленных перекрестной корреляцией между сигнальным объектом и элементами мультипликации с угловыми ориентациями , отличными от таковой сигнального объекта.
Теоретически систему, осуществляющую преобразование вращения мультиплицированного изображения можно представить в виде набора оборачивающих призм типа АР-90, расположенных по кругу, повернутых на угол a
пр/2 одна относительно другой и объединенных в один конструктивный элемент (рис.3).
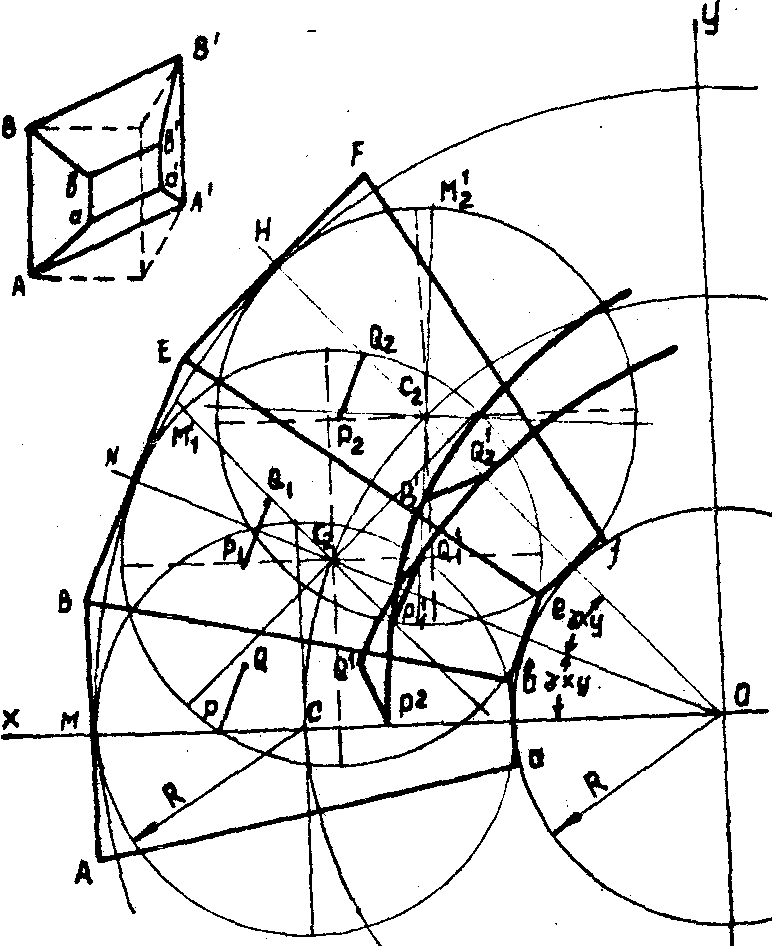
Рис.3. Проекция входных поверхностей системы оборачивающих призм на плоскость х0у .
На рисунке АВА'В' - поверхность полного внутреннего отражения призмы, А'В'а'в' -выходная поверхность.
- 293 -
К-тая призма в такой системе будет осуществлять поворот К-той позиции мультипликации на угол a
пр относительно (k-1)-ой позиции.
Условием попадания К-той позиции мультипликации на соответствующую призму является
a2k + b2k = 4r2
x2 + y2 £
4r2sin2(a
пр/4) (8)
т.е. образующей мультипликации должна быть окружность с радиусом 2 r, и максимальные размеры изображения ¦
(х,у) не должны превышать диаметр окружности с радиусом 2rsin(a
np/4).
Рассмотрим поворот мультиплицированных образов pq, p1q1,...Рnq n, b такой системе. Для точки Р с координатами (2r+Хр;0) в выходной плоскости получается изображение Р' с координатами (2r-xp;0). Координаты точки Р1 (второй позиции в мультипликации) равны
x = 2rcos(a
/2) + xp
y = 2rsin(a
/2) (9)
Для определения преобразованных координат в выходной плоскости необходимо перейти к повернутой системе координат, соответствующей призме с входной поверхностью ВЕве (ось абсцисс должна быть расположена нормально к поверхности полного внутреннего отражения). Координаты точки Р< в повернутой системе координат определяются:
x1 = 2r + xp cos(a
/2)
y1 = -xpsin(a
/2) (10)
На основании преобразующего свойства оборачивающей призмы (x®
-x,y®
y) координаты точки Р'1 (изображения точки p1
- 294 -
в выходной плоскости) запишутся в виде :
x'1 = 2r - xpcos(a
/2)
y'1 = -xpsin(a
/2) (11)
И, наконец, в исходной системе координат x0y для точки Р, в выходной плоскости координат получим
x'1 = 2rcos(a
/2) - xpcosa
y'1 = 2rsin(a
/2) - xpsina
(12)
т.е. движение выходного изображения точки Р при прохождении её через различные положения по окружности при мулътиплицировании описывается уравнением эпициклоиды.
Точку q, не лежащую на оси 0х, для придания канонической формы записи уравнению движения выходного изображения при прохождении точки через позиции мультипликации, необходимо рассматривать в соответствующей исходной системе координат, где направление оси абсцисс ОН (рис.3) составляет угол a
с направлением оси 0х (a
= qcp).
Координаты точки q в исходной системе координат равны:
x = 2rcosa - 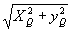
y = -2rsina
(13)
Координата точки q в повернутой системе координат, соответствующей призме АВав, определяются;
x1 = 2r + 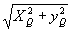 cosa cosa
y1 = 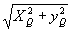 sina
(14) sina
(14)
Координаты точки q в выходной плоскости (точке q соответствует изображение q' в выходной плоскости) запишутся в виде
- 295 -
x'1 = 2r - 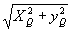 cosa cosa
y'1 = 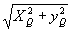 sina
(15) sina
(15)
В исходной системе координат для точки q получим координаты изображения q':
x' = 2rcosa - 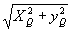 cos2a cos2a
y' = -(2rsina - 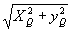 sin2a
) (16) sin2a
) (16)
Отрицательное значение ординаты в выражении (16) указывает на то, что рассматриваемая точка находится на отрицательной полуветви эпициклоиды.
В общем случае для произвольной точки К(х,у )
входного объекта ¦
(х,у)
ось абсцисс исходной системы координат составляет с осью 0х угол j
= arccos(xk/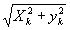 ). ).
Таким образом, совокупность точек, составлявших объекты на
входе призменной оборачивающей системы, преобразуясь, при мультиплицировании
на выходе описывает семейство эпициклоид, половине цикла которого соответствует
угол поворота исходного объекта, равный 2p рад.
Учитывая, что хк =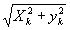 cosj
, ук= cosj
, ук=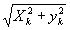 sinj
, выражение движения изображения точки К на
выходе системы можно представить в виде sinj
, выражение движения изображения точки К на
выходе системы можно представить в виде
x' = 2rcosj
- xkcosj
+ yksinj
y' = 2rsinj
- xksinj
- ykcosj
(17)
Из сравнения уравнения (17) с выражением (2) следует, что с помощью оптической системы, составленной из набора оборачивающих призм, можно осуществить преобразование вращения мультипликации двумерного образа. Таким образом, для входных образов
- 296 -
pq, Р1q 1.... p nq n (рис.3) на выходе призменной оборачивающей системы получим изображения p'q', Р'1q'1,....p'nq'n.
Реализация описанной оптической системы практически невозможна, поэтому на основе предельного перехода такая система может быть заменена телом вращения, представляющим собой двухполостный оборачивающий конус (рис.4).

Рис.4.Двухполостаый оборачивающий конус.
При переходе к двухполостному оборачивающему конусу возникают геометрические искажения, обусловленные тем, что совокупность поверхностей полного внутреннего отражения и входных плоскостей призменной системы заменяются цилиндрической и конической поверхностями, соответственно, двухполостного конуса.
На рис. 5 показана проекция входной поверхности двухполостного оборачивающего конуса на плоскость х0у. Мультиплицированными образами являются pq, p1q1,....pnqn, рассмотренные в случае призменной системы. Пунктирными линиями q',q'1,q'2 и Р',Р'1,Р'2 обозначена эпициклоиды-траектории движения изображений точек q и Р на выходе призменной системы.
- 297 -
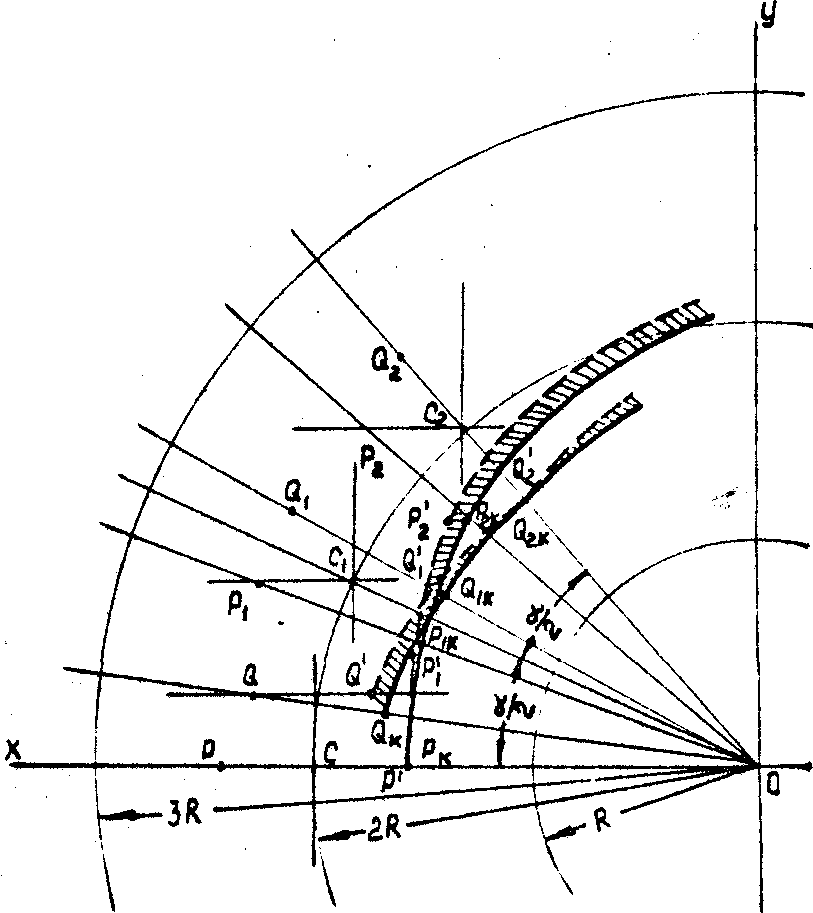
Рис. 5. Проекция входной поверхности двухполостного оборачивающего конуса,
Сплошными линиями qк,q1к,q2k и Рк,p1k,Р2k обозначены траектории движения изображений этих же точек, соответственно, на выходе конуса, Как видно из рисунка, заштрихованные части являются областями искажений, вносимых двухполостным конусом. Оценка этих искажений может быть проведена в результате анализа корреляционной функции системы оптической фильтрации. Нетрудно показать, что для случая двухполостного конуса (рис.5) уравнение движения выходного изображения произвольной входной точки К при прохождении ее через различные положения по окружности при мультиплицировавши может быть представлено в виде:
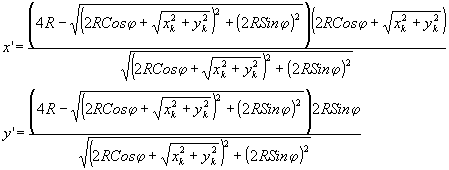 (18) (18)
- 298 -
Для произвольной точки К образа искажением является величава отрезка, соединяющего проекции выходных изображений точки на плоскости х0у для случаев призменной системы и конуса :
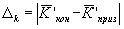 (19) (19)
Из (19) следует, что искажение для любой точки можно рассчитать по формуле:
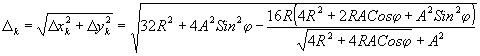 (20) (20)
где D xk=
x'кон
– x'приз;
D ук
= у'кон
– у'приз;
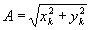 . .
В (20) модуль А может рассматриваться либо как фиксированная величина, либо как параметр. Максимальное искажение как функцию угла j
- параметра траектории движения изображения точки можно определить из условия минимизации производной от функции искажения по параметру
(D
)'j
= 0 (21)
(здесь А рассматривается как фиксированная величина).
Производная минимизируется при следующих условиях :
|
16rcos3j
+(12r3+12r2a)cos2j
+3a2cosj
-(4r3+ra2)=0 |
(22) |
|
sinj
= 0 |
|
cosj
= 0 |
На рис .6 приведена зависимость функции искажения D
от угла j
пря a=r/2. При использовании А как параметра можно найти зависимость величины искажения от протяженности объекта.
- 299 -
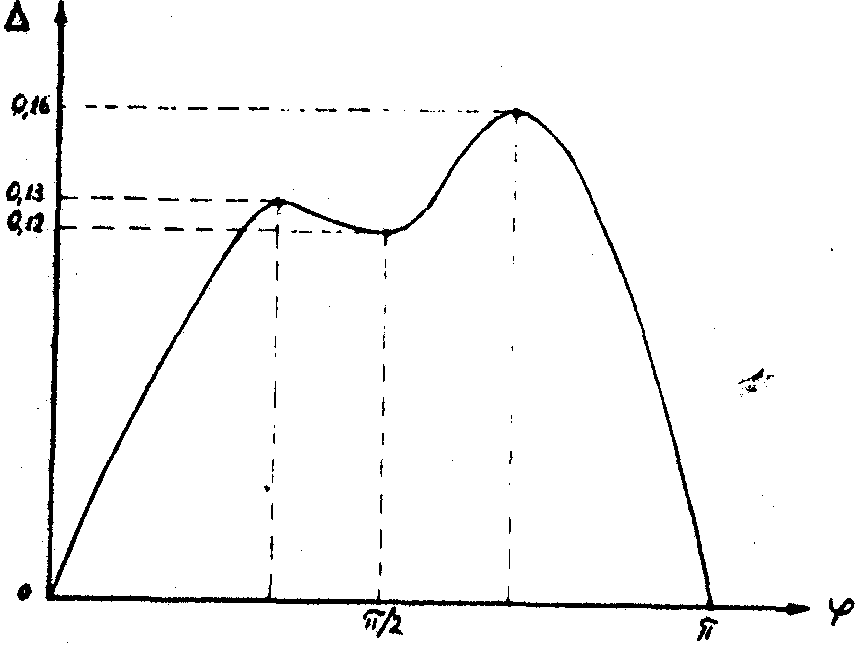
Рис.6. Зависимость функции искажения от угла j
.
На рис.7 дана эта зависимость для точки Р, принадлежащей объекту, вписанному в окружность радиуса Хр . Практически влияние этих искажений сказывается на величине сигнального отклика при фильтрация и может быть учтено выбором соответствующей величины порога. При необходимости можно осуществить коррекцию искажений на основе применения голографических корректирующих фильтров, аналогично коррекции искажений в обычных голографических системах /7/.
На рис.8 приведены результаты экспериментов: (а)- эталонный объект; (б) - (х®
-х, у®
у ) - преобразование эталонного объекта; (в)- сигнальный объект, идентичный с эталонным и повернутый на 180°; (г)- мультипликация изображения на рис.8б; так как осуществить преобразование вращения мультипликации при помощи призменной системы является практически невозможным, то для этого случая было выполнено графическое построение (рис.8д); для случая двухполостного оборачивающего конуса результат преобразования вращения мультипликация в когерентной оптической системе
- 300 -
изображен на рис.8е; на рис.8ж - результат согласованной фильтрации
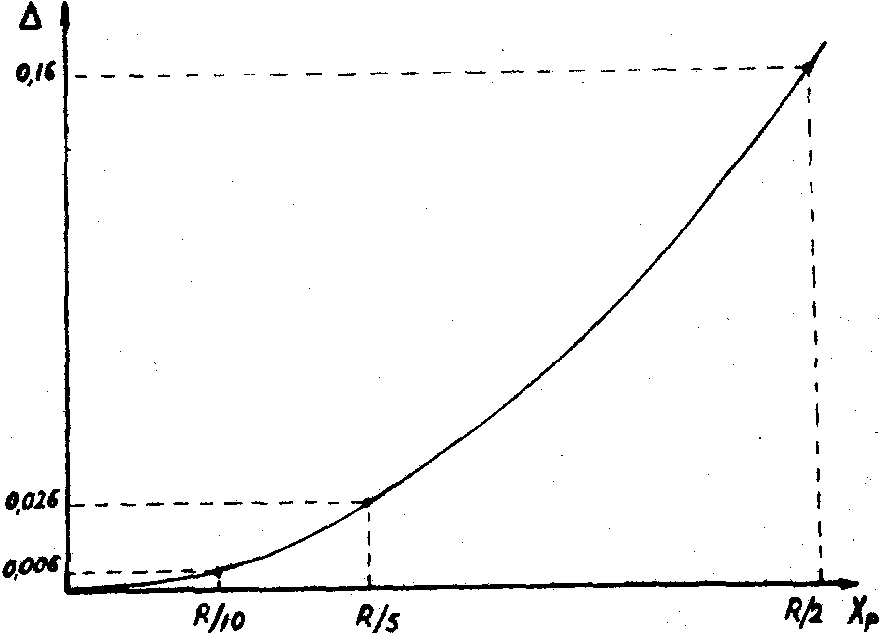
Рис.7. Зависимость функций искажения от параметра Хр.
сигнального объекта с совокупностью неискаженных изображений с различной угловой ориентацией (выход призменной системы), а на рис.8з - результат фильтрации того же объекта с совокупностью изображений, преобразованных двухполостным конусом.
Так как изображения на рис.8ж и рис.8з являются симметричными относительно каждой пары элементов мультипликации и за счет того, что одному циклу эпициклоиды соответствует двойной поворот каждого элемента мультипликации, то в результате фильтрации для каждого идентифицированного объекта получаются две яркие точки в выходной плоскости схемы фильтрации.
Операция согласованной фильтрации позволила практически оценить влияние искажений, вносимых двухполостным оборачивающим конусом, и выбрать количественное соотношение между радиусом образующей мультипликации и протяженностью объекта. Фильтрация была проведена для случая Хр =r/6. При этом для исследованного класса
- 301 -
объектов (буквы, цифры и т.д.) отношение сигнал-помеха с использованием, двухполостного конуса оказалось меньшим, чем в случае неискаженного преобразования вращения, на 1,3-1,6 дб”
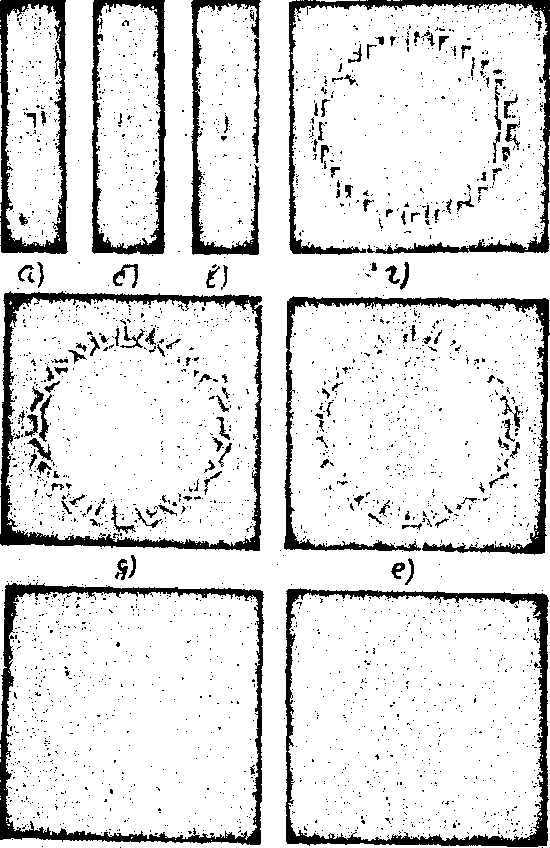
ж) з)
Рис.8. (а)-эталонный объект, (б) - (х®
-х ; у®
у) -преобразование эталонного объекта, (в) - сигнальный объект, идентичный с эталонным и повернутый на 180°, (г) - мультипликация изображения (б), (д) - преобразование вращения мультипликации, выполняемое призменной системой, (е) - преобразование вращения мультипликации, выполняемое двухполостным конусом, (ж) - результат согласованной фильтрации (в) с (д), (з) - результат согласованной фильтрации (в) с (е).
Аналогичным образом может быть рассмотрено введение в систему согласованной фильтрации инвариантности и изменение масштаба. Действительно, для этого достаточно реализовать в оптической устройстве распознавания преобразование подобия эталонного образца
- 302 -
¦
(х,у):
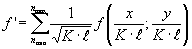 (23) (23)
где К пробегает значения натурального ряда, ℓ - масштабный фактор, величина которого выбирается в результате анализа корреляционной функции на выходе системы распознавания для реализации на входе система, принадлежащих различным классам объектов.
Литература
1. a.vander lugth. signal detection by complex spatial pilfering. ieee trans.inf.theori, it-10, v.2, p. 139-145. 1964.
2. optical and electro-optical information processing, ed.j.t. tipped et al., cambridge, mass., 1965.
3. Лу Сунь, Создание многократных изображений для интегральных схем с помощью голограмм Фурье. ТИИЭР, 56, стр.132, 1968.
4. "Зарубежная радиоэлектроника", №5, стр.70-76, 1968.
5. Вопроси радиоэлектроники. Вып.12, серия общетехническая, стр.20 1970.
6. j.e.rau, detection of difference” in real distributions. josa, v. 56, ii, p.1490, 1966.
7. y.ichiocka et al. halftone plotter and its applications to digital information processing. applied optics, v.8, 12, 1969.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

