|
|
 |
 |

|
| |
ПОКАЗАТЕЛЯ ПРЕЛОМЛЕНИЯ ФАЗОВЫХ ОБЪЕКТОВ ПО ДАННЫМ ТОПОГРАФИЧЕСКОЙ ИНТЕРФЕРОМЕТРИИ
Ю.И.Филенко
Рассмотрены основные методы восстановления показателя преломления произвольных фазовых объектов по данным голографической интерферометрии. Приводятся алгоритмы реализации методов я результаты модельных расчетов. Обсуждаются вопросы применения методов к обработке реальных экспериментальных данных.
Одним из существенных достоинств голографической интерферометрии является возможность сравнительно просто в одном эксперименте зарегистрировать интерферограымы фазового объекта, соответствующие всевозможным направлениям просвечивания. Такая практическая возможность значительно повысила интерес к разработке и анализу методов восстановления пространственного распределения показателя преломления произвольных фазовых объектов по фазовым интегралам
Ф i = ò
i¦
(x,y,z)ds i ( ¦
(x,y,z) = n(x,y,z) – n 0
где n0 - показатель преломления вне объекта), известным для всевозможных лучей t или достаточно большого их числа. Не будем здесь касаться вопросов перехода от интерферограмм к фазовым интегралам. Кроме того, сделаем упрощающее задачу предположение пренебрежимо малой рефракции света в объекте, что оправдано для многих представляющих интерес объектов, особенно при голографической интерферометрии /1/ и ограничимся случаем двух измерений. Приведенные ниже методы можно обобщить на случай трех измерений или применить последовательно к различным сечениям z.
- 270 -
Итак, рассмотрим основные методы восстановления функции по интегралам от нее Ф(r
,q
) = ò
i¦
(х,у)dsi (см. рис.1а), известных для всевозможных r
и q
или для дискретного набора r
и q
.
Фурье-синтез /2,3/
Для q
= 0, r = y
имеем 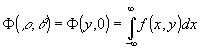 ,
где пределы интегрирования распространены на
± ¥ .
Вычисляя одномерное Фурье-преобразование от обоих частей этого соотношения,
получим: ,
где пределы интегрирования распространены на
± ¥ .
Вычисляя одномерное Фурье-преобразование от обоих частей этого соотношения,
получим:
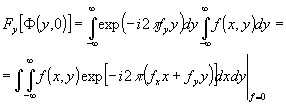 (1) (1)
То есть, зная интегралы от ¦
(х,у) вдоль направлений, параллельных оси x, можно вычислить двумерное Фурье-преобразование для прямой ¦
х = 0 (см. рис.1б). Аналогичные вычисления можно проделать для
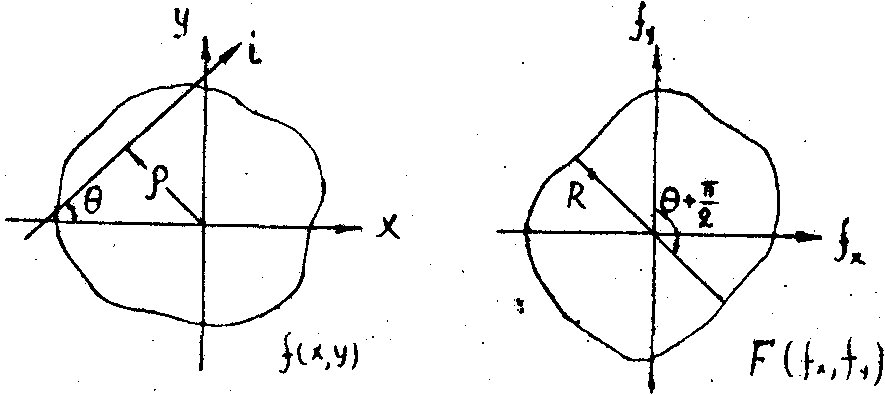
Рис.1. К Фурье-синтезу функции по фазовым интегралам”
- 271 -
всевозможных q
в диапазоне ±90°:
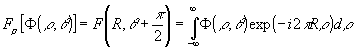 (2) (2)
Таким образом, зная интегралы для любых r
и q
, можно полностью восстановить фурье-образ f(¦
x,¦
y), а следовательно, и саму функцию
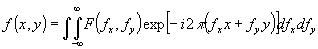 (3) (3)
Практически, как правило, имеется возможность определять по экспериментальным результатам интегралы лишь в ряде дискретных направлений q
. По r
интегралы также определяются в дискретных точках - опорных точках интерферограммы, В принципе можно интерполировать значения функции Ф(r
,q
) непосредственно в плоскости (r
,q
). Однако, при использовании дискретных данных логично пользоваться дискретным фурье-преобразованием. В этом случае в фурье-плоскости можно определить значения f(¦
x,¦
y) в дискретных точках, лежащих на дискретной последовательности прямых, проходящих через начало координат и определяемых углами наблюдения q
(см. рис.2). Формулы прямого и обратного дискретного преобразования Фурье имеют вид:
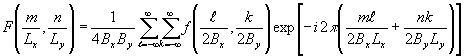 (4) (4)
и
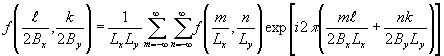 (5) (5)
где lx и ly - размеры области определения функции f(x,y), а bx и by - ее полосы частот в плоскости (¦
x,¦
y). Значения в промежуточных точках определяются выражением:
- 272 -
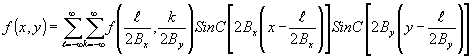 (6) (6)
где sincx = sin(p
x)/p
x
В плоскости (¦
x,¦
y) точки, в которых определяется f(¦
x,¦
y) по экспериментальным данным, не представляют собой эквидистантную систему, поэтому для выполнения обратного преобразования Фурье необходимо интерполирование данных. Если требования к частоте выборки в зависимости от спектра функции не выполняются, то можно говорить лишь о приближенном восстановлении функции. Фактически ширина фурье-спектра исходной функции не известна. Шаг выборки и по q
и по r
определяется экспериментальными возможностями. Поэтому целесообразно говорить лишь о спектре восстановленной функции. Ошибки в экспериментальных данных и ошибки метода снижают точность восстановления. В этой связи отметим, что хотя уменьшение шага выборки может не привести к соответствующему восстановлению высокочастотных составляющих функции, но создает избыточность исходных данных, что может нивелировать ошибки в предположении их некоррелированности.
На практике не всегда есть возможность обзора фазового объекта в пределах 180°. Если угол обзора составляет 2g
(см. рис.2), то в фурье-плоскости можно определить значения f(¦
x,¦
y) только внутри сектора с раскрывом 2g
. В рассматриваемом методе недостающие данные можно восстановить в фурье-плоскости. Воспользуемся соотношением, аналогичным (6):
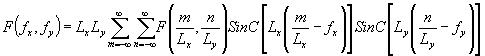 (7) (7)
Если в некотором приближении ограничиться усеченным суммированием
в (7), то
можно для различных известных f(¦
x,¦ y)
написать систему алгебраических уравнений относительно неизвестных
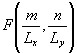 . .
- 273 -
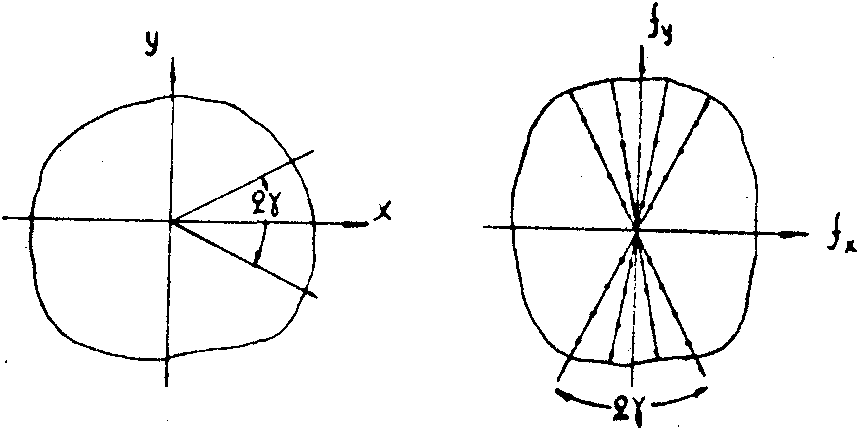
Рис.2. К дискретному Фурье-синтезу при ограниченном угле обзора.
Для решения такой системы можно воспользоваться методом, приведенным ниже для восстановления неизвестных значений в плоскости (х,у).
Обращение
Функции ¦
(х,y), заданной на плоскости, можно поставить в соответствие другую функцию Ф(i), значения которой представляют собой интегралы от ¦
(x,y) вдоль всевозможных прямых i: r
= xx
+ yh
. Функция Ф(i) является преобразованием Радона от функции ¦
(x,y). Интегралы Ф(i) можно записать в виде:
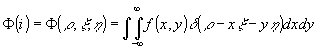 (8) (8)
где d
(r
-xx
-уh
} - d
-функция. Если ¦
(x,y) принадлежит к классу финитных бесконечно дифференцируемых функций, то существует формула обращения /4/:
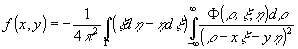 (9) (9)
- 274 -
где Г - произвольный замкнутый контур в плоскости (x
,h
), охватывающий начало координат, внутренний интеграл понимается в смысле главного значения. Если прямую i задать расстоянием r
от начала координат и углом наклона q
к оси х(-p
/2 £
q
£
p
/2), то x
= -sinq
, h
= cosq
. Учитывая, что Ф(r
,q
) = Ф(r
,q
+ p
), получим
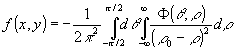 (10) (10)
где r
0 = уcosq
- хsinq
. Для вычисления внутреннего интеграла воспользуемся регуляризацией /4/:
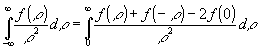 (11) (11)
Окончательно имеем
 (12) (12)
В // формула обращения в несколько ином виде получена из (3) путем перехода к полярным координатам с использованием соотношения (2):
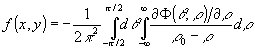 (13) (13)
где так же, как в (10) r
0 = уcosq
-xsinq
. В /5/ без ссылки на преобразование Радона соотношение (12) получено непосредственно обращением соотношения (2).
При вычислении ¦
(x, у) со формулам (10) или (13) внутренний интеграл можно рассматривать как свертку. Тогда, переходя к фурье-образу интеграла и выполняя обратное фурье-преобразование, получим:
- 275 -
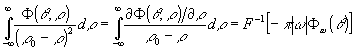 (11) (11)
где f-1 - символ обратного Фурье-преобразования, Фw
(q
] - фурье-образ Ф(r
,q
). Здесь использовалась теорема свертки, свойство дифференцирования по координате и выражения для фурье-образов обобщенных функций "главное значение 1/х" и "главное значение 1/х2":
f[p(1/x)] = -ip
sgnw
, f[p(1/x2)] = -p
|
w
|
(см. /6/).
Алгебраизация
Рассмотрим в качестве приближения ¦
(x,y) — функции, принимающую постоянное значение на участках разбиения области определения функции (см. рис.5) /7,8,3/. Она будет описываться вектором a
= (a
1,...,a
n), размерность которого n равна числу участков разбиения. В экспериментальной практике по интерферограммам, в частности голографическим, можно определить значения фазовых интегралов Фi от искомой функции вдоль некоторых прямых i. Каждой прямой соответствует линейное алгебраическое уравнение ℓi1a
1 +...+ ℓina
n = Фi, где коэффициент ℓik - длина отрезка прямой интегрирования i на участке, где функция принимает значение a
k. Аналогично можно записать m уравнений для М прямых. При произвольном выборе прямых система может быть неопределенной. Ошибки в определении правых частей и аппроксимация реальной функции ступенчатой могут привести к тому, что система будет несовместной. Поэтому можно искать лишь приближенное решение системы, удовлетворяющее некоторым дополнительным требованиям. Следует ожидать лучшее приближение, если систему заведомо переопределить (М >n), т.к. при этом могут усредняться некоррелированные ошибки измерений правых частей и ошибки, связанные с выбранной
- 276 -
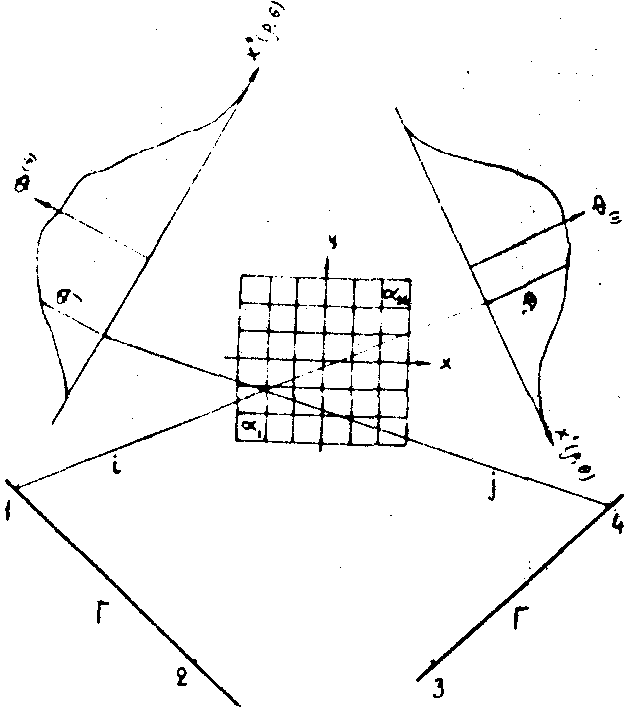
Рис.3. К методу алгебраизации:
Г - голограмма; Ф(1) - распределение фазовых интегралов при наблюдении из точки 1.
аппроксимацией функции.
Рассмотрим произвольную систему линейных уравнений:
|
ℓ11a
1 + ... + ℓ1na
n = Ф1 |
(15) |
|
ℓm1a
1 + ... + ℓmna
n = Фm |
или в матричной записи la
= Ф. Столбец a
= (a
1,...a
n) называется наилучшим приближенным решением системы (15), если для него минимизируется квадратичное отклонение
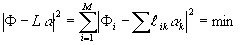 (16) (16)
- 277 -
и среди всех столбцов, для которых отклонение имеет минимальное значение, столбец a
имеет наименьшую длину
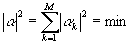 (17) (17)
Можно показать /9/, что система (15) всегда имеет одно и только одно наилучшее приближенное решение, которое определяется по формуле
a
= Д+· Ф (18)
где l+ - псевдообратная матрица для матрицы l. Удобным методом нахождения псевдообратной матрицы, не требующим вычисления детерминантов, является метод Гревилля /9/.
Известен другой алгоритм нахождения решения системы (15), удовлетворяющий условиям (16) и (17), который требует вычисления n+1 определителя nгo порядка /10/:
|
a
k = |
1 |
(ℓ1ℓ1)…(ℓk-1ℓ1)( Фℓ1)(ℓk+1ℓ1)…(ℓ1ℓn) |
(19) |
|
· · · · · · · · · · · · · · · · |
|
d |
|
(ℓ1ℓn)…(ℓk-1ℓn)( Фℓn)(ℓk+1ℓn)…(ℓnℓn) |
где ℓ1=(ℓ11,...ℓm1),... ℓn=(ℓ1n,...ℓmn), Ф=(Ф1,...Фn), d - определитель Грама g (ℓ1,...ℓn):
|
d |
(ℓ1ℓ1)......(ℓ1ℓn) |
|
· · · · · · · · · |
|
|
(ℓ1ℓn).......(ℓnℓn) |
- 278 -
Наконец, укажем еще на один алгоритм нахождения решения системы (15) /11/, программа которого на алголе приведена в /12/.
Задачу восстановления функции ¦
(х,у) по интегралам от нее можно свести к решению линейных алгебраических уравнений, используя также другие аппроксимации. В частности, функцию можно искать в виде (см. замечания по выражению (6)) /13,3/:
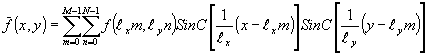 (20) (20)
где ℓх и ℓу - шаг выборки по осям х и у. При таком представлении для каждого луча интегрирования i можно написать
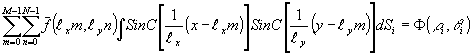 (21) (21)
здесь q
i - угол луча с осью x, r
i - расстояние от начала координат до луча. Выполняя интегрирование, для системы лучей получим систему алгебраических уравнений, число неизвестных в которых равно числу элементов выборки (Мn):
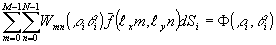 (22) (22)
где wmn(r
iq
i)=
=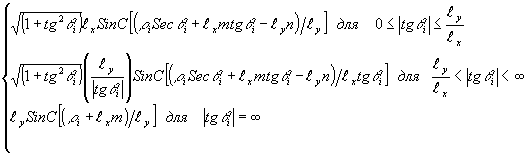
- 279 -
Другие методы
В работе /14/ распределение n(х,у) в фазовом объекте предлагалось находить вычислением последовательных поправок n1(x,y), n2(х,у) и т.д. к значению n0 вне объекта. nk(х,у) аппроксимировалась конечной суммой известных функций с неизвестными коэффициентами
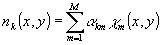 (23) (23)
Для связи т с фазовыми интегралами Ф(r
,q
) использовалось уравнение эйконала. В дальнейшем алгебраизация задачи приводила к системе уравнений с неизвестными a
km. Никаких соображений относительно метода решения системы и выбора функций c
m(х,у) авторы не приводили.
В /15/ восстанавливаемая функция разлагается в ряд по ортогональным функциям довольно сложного вида, которые инвариантны к вращению системы координат. Подстановка этого разложения в исходное интегральное уравнение и соответствующая ортогонализация позволили вычислить коэффициенты разложения. Этот метод требует знания фазовых интегралов в диапазоне 180° и хорошо работает в случае распределений ¦
(x,y), близких к осесимметричным. В произвольном случае аппроксимирующий ряд может очень медленно сходиться и требуется вычисление очень большого числа членов ряда.
Для определения значений функции в некоторых точках или коэффициентов разложения может быть применен метод последовательных приближений. К некоторым предполагаемым исходным значениям последовательными итерациями вносятся поправки по некоторому выбранному алгоритму, так чтобы лучше (иногда в некотором определенном смысле) удовлетворялось исходное в расчетах соотношение.
В /3/ для решения системы (15) использовался следующий алгоритм. Пусть D
Ф(к)i есть разность в iом уравнении после к-ой итерации:
D
Ф(к)i = Фi - ℓ ija
j (24)
- 280 -
Здесь предполагается суммирование по повторяющемуся индексу j Тогда на к+1 шаге поправка вводится следующим образом:
|
a
(k+1)j = a
(k)j + |
c·D
Фi |
ℓij |
(25) |
|
di |
где 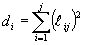 ,
а параметр c = 0,5
или меньше. Расчеты показали, что введение параметра, по крайней мере, на последних
циклах итераций, улучшает решение. Итерации продолжайте я, пока происходит уменьшение
величины (16). ,
а параметр c = 0,5
или меньше. Расчеты показали, что введение параметра, по крайней мере, на последних
циклах итераций, улучшает решение. Итерации продолжайте я, пока происходит уменьшение
величины (16).
Расчеты. Эксперимент
Для оценки точности восстановления приведенными методами выполнялись модельные расчеты. Для гладких асимметричных функций типа Гауссовых, имеющих один или два максимума в области определения, вычислялись интегралы вдоль набора лучей i, по которым восстанавливалась функция. Ошибка восстановления в отдельных точках определялась по формуле
|
d
= |
|
¦
действ - ¦
восст|
|
|
(26) |
|
¦
макс |
Такой критерий определяет правильность восстановления характера функции, а при алгебраизапии соответствует, требованиям (16,17), хотя относительная ошибка для больших и малых значений функции может быть существенно разной.
Функция восстанавливалась на ЭВМ
/3/ (см. также
/5/) по формулам
(2), (7), (13), (15), (22), (25). Использовалось
по 19 значений интегралов (r
) в каждом из
(16) направлений
(q ). Сравнение
с исходной функцией производилось в 81
точке (решетка 9х9 в плоскости х,у),
в которых функция восстанавливалась или к которым проводилась интерполяция восстановленных
значений. Когда общий диапазон q
составлял
180°, все методы дали примерно одинаковую величину
усредненного значения 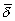 — 1,5% для разных функций. Максимальная ошибка
лежала в пределах 5%.
В этом случае, при алгебраизации число неизвестных равнялось 49 (7х9), а число
— 1,5% для разных функций. Максимальная ошибка
лежала в пределах 5%.
В этом случае, при алгебраизации число неизвестных равнялось 49 (7х9), а число
- 281 -
уравнений - 304 (16х19).
Расчет по формулам (7), (15), (22), (25) возможен при меньшем диапазоне углов интегрирования; для диапазона углов в 45° при том же числе интегралов средняя ошибка возросла до 5-9%, а максимальная - до 14-27%. При этом число неизвестных равнялось 15 (3х5), т.е. степень переопределенности системы возрастала.
С практической точки зрения представляет интерес точность восстановления при уменьшении числа известных интегралов, в особенности за счет уменьшения количества направлений интегрирования (уменьшение количества направлений регистрации интерферограмм). При восстановлении функции, линейно возрастающей на двухмерной области определения методом решения системы (15) 50 уравнений с 36 (6х6) неизвестными /7/ средняя (по 36 точкам) ошибка составляла 1,5%, максимальная - 7%. Такого же порядка средняя ошибка возникала при восстановлении функций типа распределения Гаусса по формуле (12) для 4 направлений интегрирования (через 45°) /16/.
В задачах, подобных рассматриваемой, весьма большую роль играют вопросы устойчивости решения к ошибкам значений интегралов. Для проверки устойчивости восстановления функции параболического вида методом решения системы 50 уравнений с 36 неизвестными правые части системы искажались по случайному закону на ±1,5% от максимального значения интегралом, что соответствует экспериментальному определению фазовых интегралов с точностью l
/10. Усредненная ошибка восстановления составила 4%. В аналогичном случае при расчете по формуле (22) устойчивость была значительно ниже. Восстановленная функция не имела ничего общего с исходной.
Наконец, сделаем ряд замечаний в связи с восстановлением D
n(x,у) по результатам голографической интерферометрии пламени. Хотя вопросы экспериментальной техники определения фазовых интегралов здесь не рассматриваются, приведем на рис.4 простую схему получения голограмм с большим углом обзора объекта (до 180°), удобную для реализации на стандартном голографической оборудовании.
При аппроксимации восстановленной функции ступенчатой область ее определения эллиптической формы разбивалась на 8 поясов равной ширины, пояса по периметру делились еще на насколько участков -
- 282 -
- всего 36. 50 уравнений задавались лучами, проведенными из 4 точек голограммы с общим углом обзора в 135°. Восстановленные по формуле (18) значения дали весьма нерегулярную картину и лишь усреднения полученных значений по поясам, внутри которых априорно можно было предположить постоянство функции, выявили характер поведения искомой функции. Замена 3-4 уравнений (другое проведение лучей интегрирования) приводила к существенному изменению отдельных восстановленных значений. В связи с этим отметим, что, вообще говоря, необходимо минимизировать норму разности истинной и аппроксимирующей функций на всей области определения, а в методе (15) это делается лишь на прямых интегрирования. Эти два требования почти совпадут, если линии интегрирования будут покрывать исследуемую область достаточно плотно.
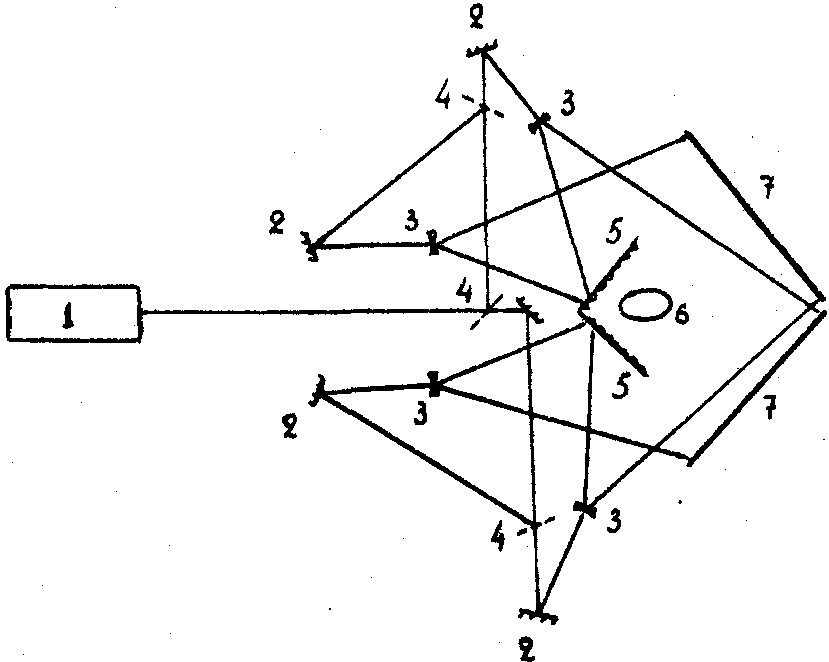
Рис. 4. Схема получения голограмм с большим углом обзора:
1 - лазер; 2 - глухое зеркало; 3 - отрицательная линия; 4 - полупрозрачное зеркало; 5 - диффузор; 6 - объект; 7 - голограмма.
- 283 -
При восстановлении этой же функции по формуле обращения (12) с 4 направлениями интегрирования также получилось довольно нерегулярное распределение. В этом случае полученные локальные значения функции мало достоверны. Однако, усреднение по некоторым соседним областям давали результаты, хорошо совпадающие с соответствующими усредненными значениями, полученными предыдущим методом.
Заключение
Приведенные методы в целом можно разделить на два класса: либо та или иная форма обращения ((2), (12), (13) определение коэффициентов разложения, как в /15/), либо тот или иной метод алгебраизации ((7), (15), (22)), в этом случае к решению могут предъявляться какие-то дополнительные требования, например (16), (17), а вычисления выполняются по тому или иному алгоритму (18), (19), (25) и т.д.
В первом случае требуется экспериментальное определение фазовых интегралов в диапазоне 180°. В то же время формула (12) проста в смысле подготовки данных для счета.
При алгебраизации задачи не требуется полного "обзора" восстанавливаемого распределения. Разные способы алгебраизации не эквивалентны по отношению к устойчивости решения и требованиям к степени переопределения системы.
Рассматриваемая задача относится к некорректным обратным задачам. Существуют и другие методы решения таких задач, например, статистические /17/.
Однако, в приведенных методах нигде в явном виде не упоминается о некорректности и связанных с нею проблемах, как это нередко бывает в подобных задачах обработки экспериментальных данных.
Высокая точность восстановления в модельных расчетах не должна приводить к выводу, что задача решена и существует целый ряд алгоритмов обработки голографических интерферограмму. Проблема устойчивости и реальные ошибки экспериментальных результатов создадут немало трудностей. В то же время приведенные выше неудовлетворительные результаты обработки эксперимента не должны порочить
- 284 -
методы восстановления функций. Они основаны на низкой точности обработки экспериментальных данных, а также на малом числе направлений интерферометрии и недостаточном переопределении расчетной системы уравнений.
Значительное повышение точности определения фазовых интегралов и выбор оптимального алгоритма восстановления показателя преломления с учетом экспериментальных возможностей и априорных данных об исследуемом объекте позволят практически реализовать большую информативность голографической интерферометрии.
Литература
1. В.М.Гинзбург. Ю.И.Филенко. ЖТФ, т.40. № 10, 1970.
2. p.d.rowley. j.opt.soc.am., 59, 1496, 1969.
3. d.w.sweeney, С.М.vest. appl.opt., v.12, n 11, 1973.
4. И.М.Гельфанд, М.И.Граев, Н.Я.Виленкин. Интегральная геометрия и связанные с ней вопросы теории представлений. М., ГИФМЛ, 1962.
5. h.g.junginger, w.van haeringen. opt.commun., 5, 1, 1972.
6. Л.М.Сороко. Основы голографии и когерентной оптики. М., "Наука", 1971.
7. Ю.И.Филенко, В.А.Фадеев, И.Н.Штейн. Доклад на i Всесоюзной конференции по голографии. Тбилиси, 1972. Проблемы голографии, вып.3, М., 1973.
8. h.h.ghau, o.s.p.zucker. opt.commun., v.8, n 4, 1973.
9. Ф.Р.Гантмахер. Теория матриц. "Наука", 1966.
10. Г.Е.Шилов. Математический анализ. Конечномерные линейные пространства. "Наука", 1969.
11. g.golyb. numer.math., 7, 206, 1965.
12. j.h.wilkinson, c.reinach. handbook for automatic computation-linear algebra (springer-verlag, berlin), v.2, 1972.
13. d.w.sweenoy, c.m.veat. appl.opt., v.11, n 1, 1972.
14. k.iwata, r.kagata. j.opt.soc.am., 63, 133, 1970.
15. r.d.matulka, d.j.collins. j.appl.phys., 42, 1109, 1971.
16. Л.Н.Прохорова. Труды ВНИИОЧИ. "Голография", вып.3, 1974.
17. В.Ф.Турчин, b.П.Козлов, М.С.Малкевич. УФН, т.102, вып.3, 1970.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

