|
|
 |
 |

|
| |
РАСЧЕТ ГОЛОГРАФИЧЕСКИХ ИНТЕРФЕРОГРАММ ОТРАЖАЩИХ ОБЪЕКТОВ
Н.Г.Власов, А.Е.Штанько
Кратко рассмотрены основные методические вопросы получения количественных данных по интерферограммам, восстановленным тремя одновременно записанными голо -граммами исследуемого объекта.
Введение
В голографической интерферометрии, в отличие от классической, класс исследуемых объектов значительно расширился, включив в себя трехмерные диффузно-отражающие объекты. Вместе с тем это привело к существенному усложнению методов расчета интерферограмм, что объясняется, главным образом, значительно больший объемом информации, которую содержит интерферограмма диффузно-отражающего объекта. Увеличение информации связано как с переходом к исследованию объектов произвольной формы, так и с тем, что интерферограмма диффузно-отражающего объекта регистрирует смещение точек его поверхности по всем трем направлениям, в отличие от интерферограммы зеркально отражающего объекта, регистрирующей смещение только по нормам к поверхности.
К настоящему времени расчету голографических интерферограмм посвящено большое число работ. Большинство предложенных способов расчета основано на использовании соотношения < связывающего разность хода лучей, рассеянных точками поверхности объекта в смещенном и несмещенном положениях с вектором перемещения этих точек /1,2/:
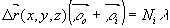 (1) (1)
- 260 -
где 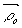 - единичный вектор, направленный по лучу, освещающему
исследуемую точку объекта,
- единичный вектор, направленный по лучу, освещающему
исследуемую точку объекта, 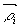 - единичный вектор в направлении наблюдения
той же точки на восстановленном изображении,
ni - порядковый номер наблюдаемой
на ней интерференционной полосы, l
- длина волны, (х,у,z)
- координаты поверхности объекта. Расчет интерферограмм
заключается в определении проекций вектора
- единичный вектор в направлении наблюдения
той же точки на восстановленном изображении,
ni - порядковый номер наблюдаемой
на ней интерференционной полосы, l
- длина волны, (х,у,z)
- координаты поверхности объекта. Расчет интерферограмм
заключается в определении проекций вектора 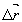 .
Анализ литературных данных показывает, что с точки зрения возможности автоматизации
процесса расшифровки интерферограмм наиболее перспективный представляется метод,
заключающийся в получении
трех интерференционных картин с различных направлений наблюдении .
Анализ литературных данных показывает, что с точки зрения возможности автоматизации
процесса расшифровки интерферограмм наиболее перспективный представляется метод,
заключающийся в получении
трех интерференционных картин с различных направлений наблюдении
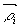 (i=1,2,3 -
номер направления наблюдения) и решение системы из трех уравнений вида
(1) /2,3/. Так как точность измерения повышается
а увеличением углов между направлениями наблюдения /4/, необходимо записать
или одну высокоапертурную голограмму, или три отдельных голограммы, каждая из
которых позволяет получить соответствующее уравнение. Получение высокоапертурной
голограммы встречает серьезные технические трудности, поэтому ниже анализируется
только вариант с тремя голограммами. Имея ввиду время, отведенное на лекцию,
ограничимся только кратким рассмотрением связанных с ним основных методических
вопросов. (i=1,2,3 -
номер направления наблюдения) и решение системы из трех уравнений вида
(1) /2,3/. Так как точность измерения повышается
а увеличением углов между направлениями наблюдения /4/, необходимо записать
или одну высокоапертурную голограмму, или три отдельных голограммы, каждая из
которых позволяет получить соответствующее уравнение. Получение высокоапертурной
голограммы встречает серьезные технические трудности, поэтому ниже анализируется
только вариант с тремя голограммами. Имея ввиду время, отведенное на лекцию,
ограничимся только кратким рассмотрением связанных с ним основных методических
вопросов.
1. Получение трех интерферограмм исследуемого объекта
Каждый из коэффициентов уравнения (1) представляет собой сумму направляющих косинусов оснащающего луча и направления наблюдения, поэтому коэффициенты могут быть найдены, если известны углы, составленные направлениями наблюдения и освещения со всеми осями выбранной системы координат. Углы освещения и наблюдения будут постоянны по всему объекту и их требуется измерить лишь один раз, если освещение и наблюдение исследуемого объекта производят в параллельных пучках. Однако, помимо усложнения голографической схемы, размеры исследуемых объектов будут ограничены размерами коллимирующих линз. В общем случае освещающий источник и точка наблюдения находятся на конечном расстоянии от объекта, и направляющие косинусы меняются при переходе от одной точки объекта к другой, что вызывает необходимость их вычисления для всех точек объекта, в
- 261 -
которых производится вычисление вектора перемещения 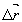 .
Такую трудоемкую работу естественно выполнить при помощи ЭВМ. Для этого, а также
для определения одних и тех же точек объекта на различных интерферограммах,
на объект проектируется ортогональная сетка линий с постоянным шагом, что можно
сделать, например, путем введения фотопластинки с отпечатанной на ней сеткой
в освещающий пучок. Пересечения линий сетки отмечают па объекте точки, в которых
будет затем вычисляться вектор перемещения. Зная шаг сетки и ее расстояние до
источника освещения, легко вычислить направляющие косинусы вектора .
Такую трудоемкую работу естественно выполнить при помощи ЭВМ. Для этого, а также
для определения одних и тех же точек объекта на различных интерферограммах,
на объект проектируется ортогональная сетка линий с постоянным шагом, что можно
сделать, например, путем введения фотопластинки с отпечатанной на ней сеткой
в освещающий пучок. Пересечения линий сетки отмечают па объекте точки, в которых
будет затем вычисляться вектор перемещения. Зная шаг сетки и ее расстояние до
источника освещения, легко вычислить направляющие косинусы вектора 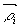 для всех узлов сетки.
для всех узлов сетки.
После обработки голограмм их устанавливают на место, которое
они занимали в процессе экспонирования, и производят фотографирование восстановленных
изображений. При этом на фотопленку осуществляется проектное отображение восстановленного
изображения объекта через переднюю главную точку фотообъектива /5/. Если относительное
отверстие объектива мало (к чему обычно стремятся для повышения контраста интерференционных
полос на фотографиях), то каждая точка объекта "наблюдается" фотоаппаратом по
определенному направлению, причем ото направление наблюдения определяется однозначно
координатами изображения точек объекта на фотографии, координатами передней
главной точки фотообъектива и расстоянием между задней главной точкой объектива
и плоскостью фотографического изображения. Таким образом, замеряя на фотографиях
координаты узлов сетки, спроецированной на объект, с помощью простых соотношений,
известных из аналитической геометрии можно вычислить направляющие косинусы векторов
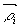 . .
2. Определение интерференционной полосы нулевого порядка
Определение порядковых номеров ni интерференционных полос в голографической интерферометрия усложнено тем, что полоса нулевого порядка nо не является ахроматической, как это может место в классической интерферометрии. Иногда она может быть найдена из условий эксперимента. Например, для жестко закрепленного объекта нулевая полоса проходит через точки закрепления, не испытывающие
- 262 -
деформации. Если голограмма стягивает большой телесный угол при объекте, или ni резко возрастает от нулевого значения, nо находится как единственная, не изменяющая своего положения при изменении угла наблюдения /6/. Более точные способы, требующие однако записи дополнительных голограмм, предложены в /7-8/.
Полоса нулевого порядка часто отсутствует на восстановленном изображении. В этом случав ее можно "создать" искусственно, соединив объект эластичной связкой с неподвижной опорой и записывая объект на голограмму вместе со связкой и опорой /9/. При использовании эластичной связки для определения порядков полос следует по возможности устранить ее влияние на смешение самого объекта. Для этого необходимо, чтобы сила, с которой связка действует на объект, была бы значительно меньше тех воздействий на объект, влиянии которых изучается в данном эксперименте. В большинстве случаев подходящим эластичным материалом для связки является вакуумная резина: она достаточно хорошо отражает красный свет. Узкую полосу из этой резины следует прикреплять к объекту так, чтобы обеспечить легкий ее натяг. Это обеспечит неподвижность связки во время экспонирования. Для крепления следует выбирать на объекте точки, которые предположительно будут испытывать малые смещения, что позволит избежать появления слишком частых интерференционных полос на связке. С другой стороны, следует принять меры по защите неподвижной опоры от воздействий, оказываемых на объект. Например, при исследовании термических деформаций, во избежании нагрева неподвижной опоры, ее следует защитить нетеплопроводным экраном, а длину связи по возможности увеличить для уменьшения теплопередачи через связку. Крепление связки к объекту лучше всего осуществлять с помощью полимеризующегося клея, например, эпоксидной смолы. Однако, в задачах, требующих полной бесконтактности измерений, применение эластичной связки недопустимо. Расшифровка интерферограмм в этом случае может быть осуществлена по методу, предложенному в /1/ и заключающемуся в подсчете числа интерференционных полос, пересекающих исследуемую точку объекта при трехкратном изменении направления наблюдения и решении соответствующей системы из трех уравнений. Достоинство метода состоит в том, что при вычислении вектора перемещения исследуемой точки оперируют не с порядковыми
- 263 -
номерами интерференционных полос, а с разностями порядковых номеров. Однако этот метод трудно автоматизировать. По мнению авторов, его целесообразно использовать для пересчета разностей порядков интерференционных полос в порядки интерференционных полос только для какой-либо одной точки объекта, что позволяет дальнейшем использовать эту точку в качестве начала отсчета для определения порядков остальных интерференционных полос. Подробное изложение такого бесконтактного способа определения начала отсчета с соответствующими формулами пересчета можно найти в работе /10/.
3. Подсчет порядковых номеров интерференционных полос
Наличие полосы нулевого порядка на объекте, либо на неподвижной опоре, которую мы можем условно считать частью объекта, не является достаточным условием для однозначного определения порядковых номеров интерференционных полос. Эта неоднозначность возникает, когда на поверхности объекта есть участки, в которых номера интерференционных полос принимают экстремальные значения, вследствие чего прямой подсчет номеров полос по их числу, укладывающемуся между полосой нулевого порядка и данной интерференционной полосой становится невозможным. Более того, если три различных направления наблюдения обеспечиваются одновременной записью трех отдельных голограмм, то при наблюдении с каждой из голограмм можно отсчитывать номера интерференционных полос от несмещенной точки объекта, либо положительную, либо в отрицательную сторону, в связи с чем имеется возможность присвоения любой точке объекта нескольких различных сочетаний номеров n1, n2, n3, соответствующих наблюдениям через первую, вторую и третью голограммы соответственно. Поскольку методы устранения указанных неоднозначностей не описаны в литературе, рассмотрим их подробнее.
Пусть размер каждой из трех голограмм позволяет менять угол наблюдения объекта в определенных пределах. Наблюдая смещения интерференционных полос при изменении угла наблюдения, можно обнаружить точки экстремальных смещений на объекте: полосы либо стягиваются к этим точкам, либо зарождаются на них и расходятся в стороны. Неоднозначность в сочетаниях знаков интерференционных полос также устранима путем наблюдения смещения интерференционных
- 264 -
полос при изменении угла зрения. Чтобы показать это, рассмотрим
сначала интерференционную картину, образованную в пространстве произвольной
точной объекта, зарегистрированной в двух положениях: смещенном и несмещенном.
Такая картина представляет собой семейство гиперболоидов вращения с общей осью,
проходящей через первоначальное и смещенное положение точки. На расстоянии,
значительно превышающей величину смещения, гиперболоиды апроксимируются конусами
вращения, являющимися их асимптотами /11/.
При наблюдении рассматриваемой точки объекта по всем направлениям, лежащим на
поверхности какого-либо из указанных конусов, через нее будет проходить интерференционная
полоса одного порядка. Геометрическое место направлений наблюдения, под которыми
в рассматриваемой точке видна интерференционная полоса нулевого порядка, представляет
собой конус, с образующей, являющейся зеркальным отражением освещающего луча
от вектора перемещения исследуемой точки, т.к. для такого направления вектора
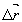 и
и 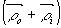 ортогональны и из (1) следует,
что
ортогональны и из (1) следует,
что
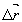 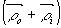 = 0 (2)
= 0 (2)
По направлениям, лежащим внутри и вне этого конуса, порядковые номера интерференционных полос имеют противоположные знаки.
Вопрос о сочетании знаков при поморах интерференционных полос сводится, следовательно, к расположению направлений наблюдения, обеспечиваемых каждой из трех голограмм, относительно конуса направления наблюдения полосы нулевого порядка. Для определения положения указанного конуса будем менять направления наблюдения в пределах апертуры каждой голограммы таким образом, чтобы интерференционные полосы на восстановленном изображении объекта смещались от нулевой полосы, проходящей через неподвижную точку объекта. Порядки интерференционных полос в близлежащих точках тогда будут уменьшаться. Это означает , что точки наблюдения в результате изменения направления наблюдения приближается к поверхности нулевого конуса. Таким образом, на каждой из голограмм мы можем обнаружить направления, в которых необходимо смещать точки наблюдения, чтобы достичь поверхности нулевого конуса. На рис.
- 265 -
приведены все возможные сочетания взаимного расположения трех голограмм и поверхности конуса для конкретной голографической схемы. Стрелками показаны направления, в которых необходимо изменять угол наблюдения, чтобы порядок интерференционных полос уменьшался. В случаях б, в, г голограммы расположены по разные стороны от поверхности конуса, и номера интерференционных полос на них имеют противоположные знаки. В случаях д, е знаки номеров интерференционных полос на всех трех голограммах одинаковы.
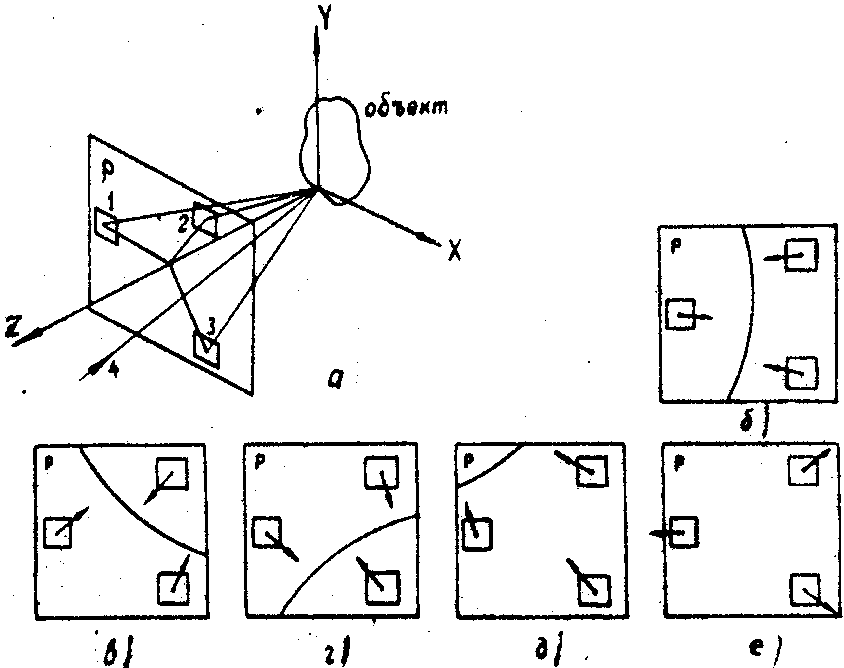
Рис. Различные случаи взаимного расположения 5-х голограмм и конуса направлений наблюдения полосы нулевого порядка:
а - геометрия голографической схемы (1,2,3 - голограммы, 4 - направление освещения);
б -е - положения линии пересечения конуса с плоскостью голограмм Р (в случае е конус не имеет пересечения с плоскостью Р). Стрелками указаны направления смещений точек наблюдения, в которых порядки интерференционных полос уменьшаются.
- 266 -
Таким образом, наблюдение смещений интерференционных полос в какой-либо выбранной точке объекта при изменении угла зрения позволяет устранить обе указанные выше неоднозначности в сочетаниях знаков при номерах интерференционных полос, наблюдаемых через различные голограммы. Остается лишь неоднозначность в выборе дополнительных сочетании знаков, например, + - + и - + -, которая в настоящее время является неустранимой в методе двух экспозиций к приводит к измерению смещения с точностью до знака. Описанную выше процедуру определения сочетания знаков необходимо провести лишь для какой-либо одной точки на объекте или на связке, а определение порядковых номеров интерференционных полос в остальных точках проводится путем прямого отсчета полос от этой точки с учетом выявленных экстремумов.
Изложенная методика позволяет пронумеровать все интерференционные полосы на восстановленном изображении объекта. Однако, центры светлых интерференционных полос, которые в методе двух экспозиций соответствуют целочисленные номера, необязательно совпадают с точками объекта, в которых предстоит рассчитать перемещение, поэтому возникает проблема определения дробной части номера полосы в этих точках. Из-за наличия на интерферограмме диффузно-отражающего объекта зернистого шума, использование с этой целью синусоидальной зависимости яркость точек поверхности объекта от разности фаз представляется затруднительным.
По-видимому, более приемлемым в методе двух экспозиций способом определения дробной части полосы является интерполяция полос, т.е. нахождение дробной части номера полосы по положению центров двух или нескольких ближайших интерференционных полос. В зависимости от характера полос можно использовать различные виды интерполяций: линейную, либо с помощью полиномов более высокий степени. Как и вычисление направляющих косинусов эту операцию целесообразно проводить на ЭВМ. Исходными данными для расчета являются координаты интерференционных полос на фотографиях восстановленного изображения, их порядковые номера и координаты узлов спроецированной на объект сетки. Из всех перечисленных операций, которые необходимо выполнить для получения количественных данных по интерферограммам диффузно-отражающих объектов, наиболее трудоемкой
- 267 -
является считывание координат интерференционных полос, так как его приходится производить вручную на компараторе. К настоящему времени имеется лишь одно сообщение /12/ о создании автоматической системы считывания голографических интерферограмм.
Заключение
Выбор системы декартовых координат, в которых определяются
проекции вектора 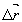 ,
обусловлен конкретной задачей эксперимента. Для решения задач, связанных с определением
смещения центра тяжести объекта под действием тепловой или механической нагрузки,
проекции вектора перемещения определяются относительно заданной системы координат,
единой для всех точек поверхности объекта. Для решения задач, заключающихся
в определении прочностных характеристик исследуемого объекта, выбирается система
координат, связанная с его поверхностью, и определяются нормальные и касательные
(по отношению к поверхности исследуемого объекта) проекции вектора перемещения.
В этом случае направление осей координатной системы изменяется по объекту в
зависимости от кривизны его поверхности, что усложняет расчет и требует знания
геометрических параметров объекта. В настоящей лекции рассматривалась задача,
относящаяся к первому из перечисленных классов, а именно расчета интерферограмм
в системе координат, единой для всего объекта. Для перехода в другую систему
координат необходимо знание геометрических
параметров объекта. ,
обусловлен конкретной задачей эксперимента. Для решения задач, связанных с определением
смещения центра тяжести объекта под действием тепловой или механической нагрузки,
проекции вектора перемещения определяются относительно заданной системы координат,
единой для всех точек поверхности объекта. Для решения задач, заключающихся
в определении прочностных характеристик исследуемого объекта, выбирается система
координат, связанная с его поверхностью, и определяются нормальные и касательные
(по отношению к поверхности исследуемого объекта) проекции вектора перемещения.
В этом случае направление осей координатной системы изменяется по объекту в
зависимости от кривизны его поверхности, что усложняет расчет и требует знания
геометрических параметров объекта. В настоящей лекции рассматривалась задача,
относящаяся к первому из перечисленных классов, а именно расчета интерферограмм
в системе координат, единой для всего объекта. Для перехода в другую систему
координат необходимо знание геометрических
параметров объекта.
В заключение укажем несколько работ /4,13,14/ в которых получены количественные данные при расчете интерферограмм отражающих объектов.
Литература
1. Е.Б.Александров, А.М.Бонч-Бруевич, ЖТФ, 37, 2, 360, 1967.
2. j.e.sollid. appl.opt., 8, 8, 1587, 1969.
4. k.shibayama, h.uchiyama. appl.opt., 10, 9, 1971.
4. t.matsumoto, k.iwata, r.nagata. appl.opt., 12, 5, 961, 1973.
5. В.Ф.Дейнеко, Аэрофртогеодезия, геодезизд., 1955.
- 268 -
6. a.e.ennos. contemp.phys., 8, 2, 153, 1967.
7. m.r.wall. appl. de l'holographie, besancon, 4.9, 1940.
У. А.С.Богомолов, Н.Г.Власов, К.Г.Соловьев. Оптика и спектроскопия. 31, № 3, 481, 1971.
9. n.abramson. appl.opt., 11, 5, 1143, 1972.
10. Н.Г.Власов, В.Н.Проценко, А.Е.Штанько. В сб. "Современные проблемы прикладной голографии". Изд. МДНТП, 1974.
11. p.m.boone, de barker l.c. optik, 37, 1, 61, 1973.
12. ЭИ. сер. Контрольно-измерительная техника, № 16, 35, 1974.
13. t.matsumoto, k.iwata, r.nagata. appl.opt., 13, 5, 1080, 1974.
14. c.a.scimmarella, j.a.gilbert. appl.opt., 12, 7, 1973.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

