|
|
 |
 |

|
| |
МЕТОДЫ КОМПЕНСАЦИИ АБЕРРАЦИИ ГОЛОГРАШНОЙ ЛИНЗЫ, ОБУСЛОВЛЕННОЙ СМЕЩЕНИЕМ ДЛИНЫ ВОЛНЫ
К.С.Мустафин
Рассмотрена возможность полной компенсации сферической аберрации голограммной линзы путей оптимизации геометрии пучков, а также с помощью плоскопараллельной пластинки. Приводятся экспериментальные данные.
Известно, что если реконструирующая волна не идентична референтной (опорной) волне, то возникают различные аберрации. Например, изменение длины волны при реконструкции неизменно ведет к возникновению сферической аберрации. Представляет интерес исследовать возможность уменьшения такой аберрации, так как на практике встречаются случаи, когда голограмма изготавливается на одной длине волны, а восстановление ведется на другой длине волны. Особенно часто такие случаи могут иметь место при использовании голограмм для формирования изображений.
В работе /1/ рассмотрена возможность компенсации аберраций голограмм, обусловленных смещением длины волны и предложен метод балансирования аберраций. По этому методу условия голографирования и восстановления выбирают таким образом, чтобы аберрация комы была равна нулю по всей апертуре голо граммы, а максимальное значение сферической аберрации было равно и противоположно по знаку максимальному значению аберрации астигматизма.
Применение ЭВМ позволяет найти оптимальные условия голографирования и восстановления, при которых суммарные аберрации минимальны.
Применение этого метода на случай толстослойных голограмм рассмотрено в работе /2/. Хотя указанные методом и не достигается полная компенсация аберраций по всей апертуре голограмм, но
- 239 -
удается существенно уменьшить их при небольших апертурах голограмм.
Ниже будут рассмотрены возможности полной компенсации по всей апертуре сферической аберрации голографической линзы, обусловленной смещением длины волны.
1. Компенсация сферической аберрации путем оптимизации условий освещения при реконструкции
Если голограммная линза (или голограмма объекта в виде точечного источника) изготовлена с использованием лазера длины волны l
0 и используется в монохроматическом свете с l
¹
l
0, то такая линза будет обладать сферической аберрацией. При этом зная продольной сферической аберрации D
ru будет зависеть от величины m
= l
/l
0: D
ru < 0 при m
> 1 и D
ru > 0 при m
< 1.
В то же время при l
= l
0 голограммная линза восстанавливает аберрированную волну, если геометрия реконструирующей волны не соответствует геометрии референтной волны. Если же изменить и длину волны и геометрию реконструирующего источника так, чтобы возникающие при этом аберрации были противоположны по знаку, то они будут взаимно компенсировать друг друга. Покажем, что таким путем можно достичь полной компенсации сферической аберрации, обусловленной смещением длины волны.
Напишем выражения для коэффициента сферической аберрации плоской голограммы при m
¹
1 /3/.
 (1) (1)
где rb, ru, rc и r0 - расстояния от голограммы до точечных источников восстановленной, восстанавливающей, сигнальной и опорной волн, соответственно; верхний знак относится к мнимому, а нижний - к действительному изображениям.
Кроме того имеется формула линзы:
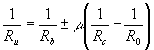 (2) (2)
Приравнивая в (1) А00 = 0 и решая уравнения (1) и (2) совместно,
- 240 -
получим:
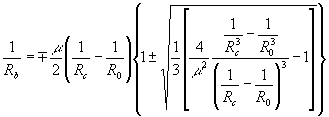 (3) (3)
Уравнение (3) определяет оптимальное расстояние rb от восстанавливающего точечного источника до центра голограммы, при котором сферическая аберрация полностью компенсируется для длины волны l
= l
0m
.
Определим пределы применимости метода. Для этого рассмотрим частный случай r0 = ¥
. Тогда из (3) имеем:
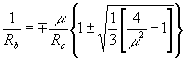
откуда видно, что rb имеет действительные значения только в области m
£
2.
Рассмотрим теперь коэффициенты комы. Для простоты ограничимся случаем одноосевой голограммы. Тогда, ввиду осевой симметрии, достаточно рассмотреть аберрации комы одномерной (ось Х) голограммы /3/:
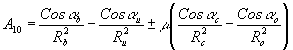 (4) (4)
где a
i - угол, образуемый волновым вектором i-той волны к с осью Х; i = b, u, c, o.
Пусть cosa
с = cоsa
о = 0.
Тогда можно показать /3/, что cosa
u = cosa
b.
Учитывая это, получаем:
a10 = (1/r2b – 1/r2u)·cosa
u (5)
Из (3), (2) и (5) имеем:
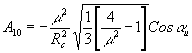 (6) (6)
- 241 -
Если бы голограмма освещалась плоской волной (без оптимизации условий), то для коэффициента аберрации комы можно было бы написать:
a'10 = (-m
2cosa
u)/rc (7)
Из сравнения (6) и (7) видно, что при m
> 1 a10 < А'10 и при m
< 1 a10 > a'10. Таким образом, при m
> 1 наряду с полной компенсацией сферической аберрации имеется возможность уменьшения аберрации комы. А при m
< 1 - кома возрастает.
При этих же условиях коэффициент астигматизма будет /3/:
a20 = (1/rb – 1/ru)·cos2a
u (8)
или с учетом (2):
a20 = ±
(m
/rc)cos2a
u (7)
Из (8) видно, что коэффициент астигматизма остается без изменений.
До сих пор мы рассматривали случай, когда при заданных rс, ro и m
необходимо было определить оптимальное значение rb, чтобы полностью компенсировать сферическую аберрацию для l
= l
0m
.
Можно, очевидно, решить и обратную задачу: определить оптимальное значение rо при заданных rb, rc и m
. Для этого приравняем к нулю коэффициент сферической аберрации a00=0 и из (1) и (2) найдем уравнение третьей степени относительно 1/ro:
a(1/ro)3 + b(1/ro)2 + c(1/ro)2 + d (9)
где
|
a = m
(1 - m
2) |
(10) |
|
b = ±
3m
2(1/rb ±
1/rc) |
|
c = - 3m
(1/rb ±
1/rc) |
|
d = - m /r3c
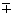 1/r3b
± (1/ro ±
1/rc)3 1/r3b
± (1/ro ±
1/rc)3
|
Уравнение (9) имеет три действительных различных корня /4/.
- 242 -
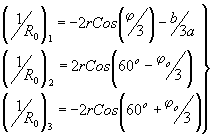 (11) (11)
где 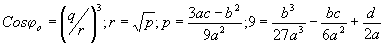
Например, для частного случая rb = ¥
, l
= 0,633 мкм, l
= 0,436 мкм, согласно (10) и (11),инеем следующие решения:
(1/r0)1 = -3,44/rc
(1/r0)2 = 1/rc
(1/r0)3 = -rc/3,44
Первый и третий корни характеризуют взаимозаменяемость объектного (rc) и восстанавливающего (rb) пучков, а второй корень r0 = rc есть тривиальный случай, когда объектный и референтный источники совпадают и, следовательно, на фотопластинке будет равномерное почернение.
Таким образом, путем соответствующего подбора геометрии интерферирующих пучков с длиной волны l
0 на стадии изготовления голограммной линзы можно сделать ее безаберрационной для другой длины волны l
и реконструирующего пучка заданной конфигурации.
2. Компенсация сферической аберрации голограммы с использованием плоскопараллельной пластинки
В ряде случаев оказывается желательным полностью компенсировать сферическую аберрацию голограммной линзы, вызванную смещением длины волны, не прибегая к подбору геометрии реконструирующей волны или интерферирующих волн при записи голограммы.
Можно показать, что использование плоскопараллельной пластинки также позволяет полностью компенсировать сферическую аберрацию.
Найдем распределение фазы волны на плоскости голограммы, когда
- 243 -
она освещена излучением от точечного источника, прошедшим через плоскопараллельную пластинку толщины d с показателем преломления материала пластинки n.
Для упрощения задачи ограничимся рассмотрением распределения фазы вдоль одной координаты на плоскости голограммы, например, координаты Х . На рис.1 показан ход луча sАВ, образующего угол j
с осью z (совпадающей с нормалью n голограммы). Начало координат О совпадает с центром голограимы.
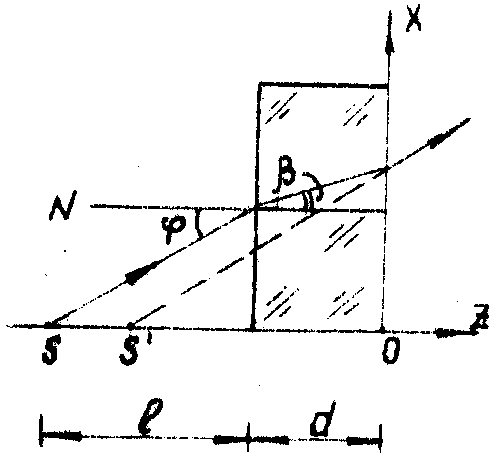
Рис.1. Ход светового луча saВ.
Для фазы волны в точке В на голограмме можно написать:
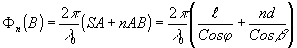 (12) (12)
где ℓ - расстояние от точечного источника s до плоскопараллельной пластинки; j
и b
- соответственно, углы падения и преломления на пластинке луча sА; l
0 - длина волны света.
Выразим cosj
и cosb
в (12) через tgj
.
При малых tgj
, пренебрегая членами выше tg4j
, будем иметь:
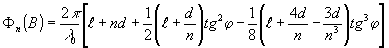 (13) (13)
- 244 -
С другой стороны,
tgj
= x/(so – ss') (14)
где x - координата точки b; s0 = ℓ + d и
ss' = d(1 - cosj
/ncosb
) (15)
Или снова выражая cosj
и Соsb
в (15) через tgj
:
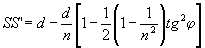 (16) (16)
Из (14) и (16) имеем:
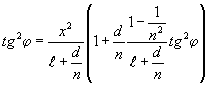
Откуда методом последовательного приближения находим:
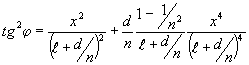 (17) (17)
и
tg4j
= x4/(ℓ + d/n)4 (18)
Подставляя значения tg2j
и tg4j
из (17) и (18) в (13), получаем зависимость фазы Фn(x) от координаты x:
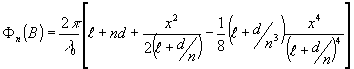 (19) (19)
Напишем фазовые уравнения голограммы:
Ф u(x) = Фb(x) ±
[ Фс(х) – Ф0(х)] (20)
где Ф u(х), Фb( х), Фc(х) и Ф0(x) - распределения фаз на голограмме восстановленной, восстанавливающей, сигнальной и референтной волн соответственно.
В дальнейшем будем рассматривать только мнимое изображение
- 245 -
(верхний знак в (20)).
Рассмотрим случай, когда в качестве опорной и восстанавливающей волн используются плоские волны, фронты которых совпадают с плоскостью голограммы.
Тогда Ф b = const и Ф0 = const и (20) принимает вид:
Ф u(x) = Фc(x) (21)
Предположим, что в качестве сигнальной волны является волна типа (19), т.е. Фс(х)= Фn(x ),и потребуем, чтобы восстановленная волна была сферической, т.е.:
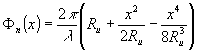 (22) (22)
Для того, чтобы была обеспечена полная компенсация сферической аберрации, необходимо, чтобы уравнение (21) после подстановки значений Фn(x) из (22) и Фс(х) из (19), удовлетворяло для любых значений координаты Х.
Приравнивая коэффициенты при х 2 слева и справа уравнения (21) находим:
m
ru = ℓ + d/n (23)
где m
= l
'/l
0; l
0 и l
' - длины волн света при голографировании и восстановлении, соответственно.
Приравнивая коэффициенты при х 4, имеем:
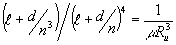 (24) (24)
Исключая из (23) и (24) ℓ, находим:
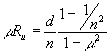 (25) (25)
Поскольку ru > 0 (рассматриваем мнимое изображение), то равенство (25) справедливо только при m
< 1.
Из рассмотренного выше видно, что можно достичь полной
- 246 -
компенсации сферической аберрации коротковолнового смещения (m
< 1) голограммной линзы, если при получении такой голограммы между сигнальным точечным источником и голограммой установлена плоскопараллельная пластинка, толщина которой удовлетворяет уравнению (25).
Рассмотрим теперь возможность компенсации сферической аберрации голограммной линзы, обусловленной длинноволновым смещением, т.е. при m
> i.
Пусть изготовлена голограммная линза с помощью точечного источника, расположенного на расстоянии rс от голограммы и плоской опорной волны, фронт которой совпадает с плоскостью голограммы. Если осветить такую голограмму нормально падающей на нее плоской волной, длина волны которой l
' > l
0 (где l
0 - длина волны при записи голограммы), то за голограммой сформируется асферическая волна. Эта волна может быть преобразована в сферическую волну при прохождении через плоскопараллельную пластинку, если распределение фазы асферической волны Фu(х) будет совпадать с распределением (19), т.е. Фu(х) = Ф'n(x). Значок штрих в Фn(х) указывает, что в (19) l
0 надо заменить на l
'.
Таким образом, вместо (21) будем иметь:
Ф 'n(x) = Фc(x) (26)
где 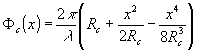 . .
Снова, как и прежде, приравнивая к нулю коэффициенты при одинаковых степенях х уравнения (26) и исключая ℓ, найдем:
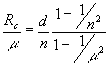 (27) (27)
По (27) можно определить толщину d плоскопараллельной пластинки, которая полностью компенсирует сферическую аберрацию, обусловленную длинноволновым смещением (m
>1).
3. Экспериментальные данные
С целью экспериментальной проверки возможности компенсации сферической аберрации плоскопараллельной пластинкой была изготовлена
- 247 -
по одноосевой схеме голограмма точечного источника с использованием плоской опорной волны. Голограмма была изготовлена с применением кадмиевого лазера типа ЛГ-31 (l
0 = 441,6 нм); максимальный радиус голограммы hmax = 6,8 мм, расстояние от точечного источника до голограммы было rс = 25 мм. Точечный источник создавался с помощью стандартного микрообъектива с числовой апертурой 0,30, помещенного в параллельный пучок лазерного излучения.
Волновые аберрации такой голограммы были исследованы при освещении ее (восстановлении) плоской волной лазерного излучения длины волны l
= 632,8 нм. Исследования проводились на интерферометре типа Цендера-Маха, в одном плече которого были помещены объектив (апохромат; 20х; 0,65) и голограмма, установленные софокусно. Компенсирующая плоскопараллельная пластинка устанавливалась между объективом и голограммой.
Интерферограмма волнового фронта, восстановленного с голограммы без компенсирующей пластинки показывала наличие 42 полос и характеризовала сферическую аберрацию голограммы, обусловленную различием длин воля света при записи (l
0 = 441,6 нм) и восстановлении ( l
= 632,8 нм). Расчет волновой аберрации по формуле /3/:
D
= h4m
(1 - m
2)/8r3c
дает величину D
= 26,1 мкм, или число полос n=D
/l
=41,5, что хорошо согласуется с экспериментальными данными (~ 42 полосы).
Такую сферическую аберрацию голограммы, согласно (27), можно компенсировать с помощью плоскопараллельной пластинки толщиной d = 24 мм с показателем преломления n=1,514 (для l
= 632,8 нм; стекло К-8). Интерферограмма при введении такой компенсирующей пластинки представляла собой равномерно освещенное поле к свидетельствовало о том, что имеет место практически полная компенсация аберраций.
Была определена также зависимость максимального разрешения, даваемого голограммой , от толщины компенсирующей пластинки. Для этого голограмма использовалась как фокусирующий элемент при получении изображения Миры № 2 из комплекта оптической скамья. Компенсирующая пластинка помещалась в сходящийся пучок сразу за
- 248 -
голограммой. Полученное изображение наблюдалось при помощи микроскопа. Источником служила ртутная лампа ДРШ-250 (l
= 546 нм). На рис.2 приведен график зависимости разрешения d
(лин/мм) голограммы вблизи оптической оси от толщины пластинки. Кривая имеет четко выраженный максимум при d = 21 мм. Максимальное разрешение голограммы при этом было близко к дифракционному пределу разрешения объектива, использованного при голографировании.
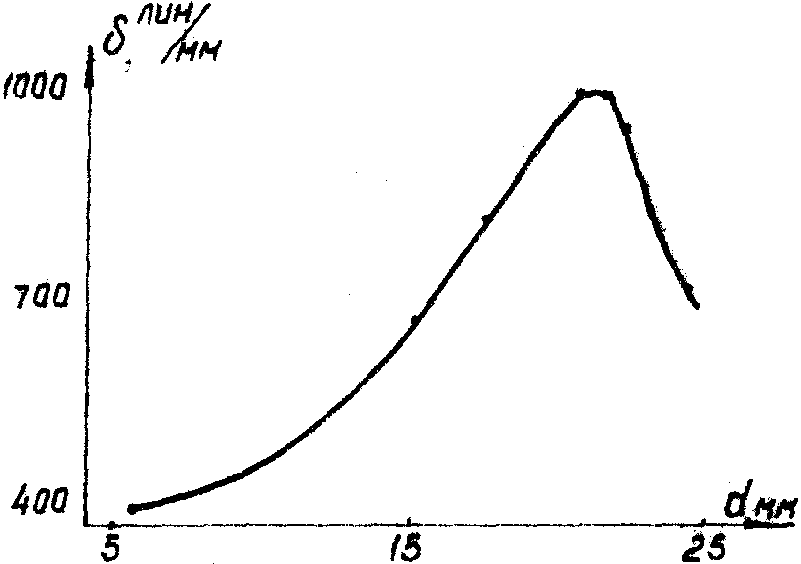
Рис. 2. Зависимость разрешения d
голограммы вблизи оптической оси от толщины пластинки d.
Таким образом, приведенные экспериментальные данные подтверждают возможность полной компенсации сферической аберрации голограмм.
В заключение отметим, что рассмотрение вклада аберрации 5-го порядка показывает, что полная компенсация аберраций указанными выше методами может быть обеспечена до значений угловых апертур j
= 18°, для значений m
и в интервале 0,7 £
m
£
1,4.
- 249 -
Литература
1. j.n.latta. appl.opt., 10, n 3, 609, 1971.
2. j.m.moran. appl.opt., 10, n 8, 1909, 1971.
3. Г.Н.Буйнов, Р.К.Гизатуллин, К.С.Мустафин. Оптика и спектр., 34, вып.4, 774, 1973.
4. И.Н.Бронштейн, К.А.Семендяев. Справочник по математике, М., 1957.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

