|
|
 |
 |

|
| |
ПРЕОБРАЗОВАНИЕ СВЕТОВЫХ ПУЧКОВ ОБЪЕМНЫМИ ДИНАМИЧЕСКИМИ ГОЛОГРАММАМИ
В.Г.Сидорович, Д.И.Стаселько
Теоретически рассмотрено взаимодействие объектной в референтной волн в процессе записи объемных голограмм в средах, изменяющих под действием света показатель преломления или коэффициент поглощения (усиления).
Изучение объемных динамических голограмм представляет значительный практический интерес в связи с возможностью их применения для управления пространственно-временными характеристиками источников когерентного излучения.
Рассмотрим теорию простейших фазовых и амплитудных динамических объемных голограмм. Пусть на границу среды, изменяющей комплексную диэлектрическую проницаемость под действием светового поля,, падают под углами ±
q
к нормали две плоские монохроматические волны с амплитудами С1(0) и С-1(0). Предполагается, что обе волны поляризованы нормально к плоскости падения и имеют одинаковую частоту w
. При этих условиях распространение света в среде можно описать стационарным волновым уравнением для амплитуды напряженности электрического поля Е
Ñ
2 Е + к20e
(Е) = 0 (1)
где к 0= w
/с - волновое число падающего излучения, e
=e
0+D
e
(e) - комплексная диэлектрическая проницаемость среды, причем |
D
e
(Е)|
<<|
e
0|
. Примем, что e
0=1, оси координат x и y
- 232 -
направим вдоль поверхности среды, ось z - ортогонально этой поверхности, x0z - плоскость падения волн. Малость изменения диэлектрической проницаемости и периодичность условий на границе голограммы позволяет искать решение уравнения (1) в виде
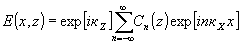 (2) (2)
где cn(z) - медленно меняющиеся функции от z, кz=к0Соsq
и кx=к0sin q
. Подставляя (2) в (1) и отбрасывая вторые производные от Сn no z, получим соотношение, связывающее амплитуды cn(z) плоских волн, распространяющихся в голограмме:
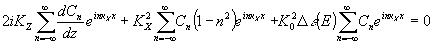 (2) (2)
При рассмотрении фазовых динамических голограмм зададимся следующими зависимостями D
e
(e):
D
e
(e) = a
|
e|
2 (4)
и
|
D
e
(e) = b
|
d|
e|
2 |
|
(5) |
|
dx |
|
Формула (4) соответствует случаю, когда динамическая решетка совпадает по положению с образующей ее интерференционной картиной, а (5) - случаю, когда решетка сдвинута относительно этой картины на четверть периода. В дальнейшем такие решетки будем называть соответственно, несмещенными и сдвиговыми. Подставляя (4) и (5) в (3) приравнивая нулю суммы коэффициентов при экспоненциальных членах с одинаковыми показателями, получим системы дифференциальных уравнений для амплитуд волн, распространяющихся в несмещенных и сдвиговых голограммах. Мы ограничимся рассмотрением в этих системах лишь нескольких уравнений, соответствующих наиболее интенсивным волнам. При этом в соответствии с важным для практики случаем, будем предполагать, что одна из падающих на голограмму волн значительно превосходит другую по амплитуде, например, |
С1(0) |
>> |
С-1(0) |
.
- 233 -
Принятые предположения позволяют при анализе несмещенных фазовых решеток рассматривать систему из трех уравнений для амплитуд волн С 1, С-1, и С3:
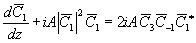 (6а) (6а)
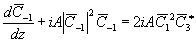
(6б)
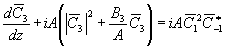
(6в)
где 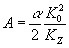 ; ;
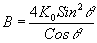 и
и 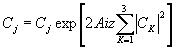 ;
j=1,2,3 ;
j=1,2,3
Из уравнений (6) следует, что для усиления амплитуды слабой исходной волны С-1 в несмещенных фазовых решетках необходимо участие волны высшего порядка (С3¹
0), причем эта волна вблизи границы голограммы как и волна С-1, усиливается экспоненциально с показателем, равным a|С1(0) |
2z . Однако из-за рассогласования фаз волн при распространении вглубь голограммы (третий член в левой части уравнения (6в)) амплитуда волны С3, а вместе с ней и С-1, эффективно усиливается лишь в слое толщиной zэф»
L
2/2 l
( L
- период интерференционной картины). Следовательно, несмещенные фазовые динамические решетки ведут себя как тонкие, независимо от их действительной толщины. Стремление повысить эффективность таких голограмм путем перехода к более объемной записи за счет увеличения угла схождения пучков может привести лишь к противоположному результату, т.к. при этом уменьшается длина эффективного усиления zэф. При достаточно больших q
пучки в таких голограммах будут распространяться практически без обмена энергией.
Наиболее существенное отличие уравнений, описывающих распространение
волн в сдвиговых голограммах, состоит в наличии членов, обеспечивающих непосредственный
обмен энергией между исходными волнами. Это позволяет, пользуясь критерием подавления
волн высших порядков 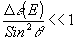 */ ограничиться при достаточно больших q
*/ ограничиться при достаточно больших q
*/ Данное условие получено в результате анализа системы из трех уравнений для С 1, С-1 и С3. Левая часть неравенства представляет собой оценку отношения амплитуд третьей и минус первой волн.
- 234 -
рассмотрением системы двух уравнений:
|
dc1 |
=-g
|
c-1|
2c1 |
(7а) |
|
dz |
|
|
dc-1 |
=g
|
c1|
2c-1 |
(7б) |
|
dz |
где g
= b
К20tg q
. Знаки правых частей уравнений (7) задаются направлением сдвига решетки относительно интерференционной картины. В данном случае предполагается, что решетка смещена в сторону волны с, . Решение уравнений (7) дает следующее выражение для интенсивности j-1(z):
|
j-1(z) = |
j1(0) + j-1(0) |
(8) |
|
1 + |
j1(0) |
exp[-g
(j1(0) + j-1(0)z] |
|
j-1(0) |
Согласно (8) на достаточно большой глубине энергия сильной волны может практически полностью перейти к первоначально более слабой волне независимо от соотношения интенсивностей этих волн на границе голограммы. Ход изменения интенсивностей волн, рассчитанный с помощью формулы (8), изображен на рис.1 для случая D
e
max=10 -5, j -1(0)/j 1(0)= 10 -8, l
=7·10 -5 см. Там же представлено распределение глубины модуляции диэлектрической проницаемости в объеме голограммы, определяемое соотношением
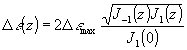
Видно, что D
e
(z) имеет максимум, ширина которого D
z определяет физическую толщину динамической голограммы и может быть приближенно оценена как D
z»
3l
/D
e
max. Оценка коэффициента усиления по интенсивности слабого пучка в слое, прилегающем к границе голограммы, дает
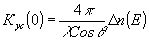 (9) (9)
где D
n(e) - характерное изменение показателя преломления среды под действием света. Подставляя в (9) l
=7·10-5 см, cosq
=1 и типичные для динамических голограмм значения D
n(Е)=10-5¸
10 -4, находим, что начальные коэффициенты усиления для динамических голограмм лежат в пределах от 2 до 20 см-1, что на два-три порядка
- 235 -
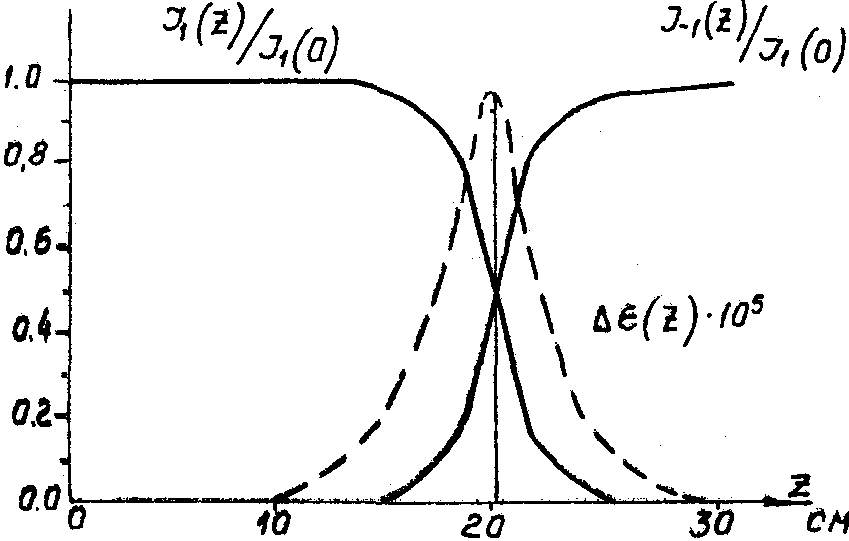
Рис.1. Кривые, показывающие ход изменения интенсивностей волн j1(z), j-1(z) и распределение глубины модуляции диэлектрической проницаемости D
e
(z) в объеме голограммы.
превосходит коэффициенты усиления, достигаемые в инверсных средах твердотельных источников когерентного излучения. Таким образом, используя динамическую голограмму как усилитель, можно добиться значительного усиления слабых сигналов при сравнительно небольших длинах усиливающего слоя. Способность сдвиговых динамических фазовых голограмм практически полностью преобразовывать падающие пучки независимо от начального отношения их интенсивностей может быть использована для стабилизации направления распространения световых пучков. Предлагаемая схема стабилизации приведена на рис.2.
Схема позволяет уменьшить изменение направления стабилизируемого телескопа.
Анализ амплитудных динамических голограмм с записью в поглощающих и усиливающих средах проведем применительно к случаю однородно уширенных линий поглощения и усиления. В соответствии с этим
- 236 -
примем */
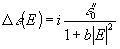 (10) (10)
где e
”0=c
0/k0, c
0 - начальный коэффициент поглощения (усиления) по интенсивности. Поглощающим средам соответствует c
0>0, а усиливающим c
0<0. Положим, как и прежде, |
С1(0) |
>> |
С-1(0) |
.
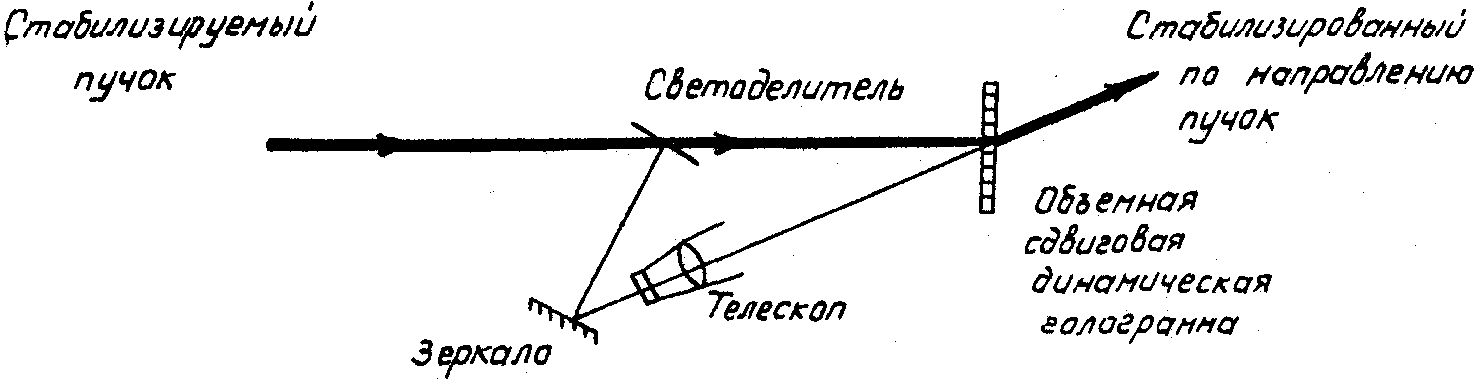
Рис.2. Схема стабилизации направления распространения световых пучков.
Условие объемности амплитудных динамических голограмм c
/k0sin2q
<<1 позволяет ограничиться рассмотрением уравнений для двух волн:
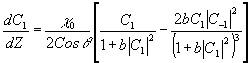 (11a) (11a)
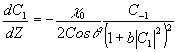
(11б)
Анализ этой системы показывает, что основным результатом
*/ Изменение действительной части D
e
(Е), обусловленное изменением коэффициента поглощения, в (10) не учитывается, что физически соответствует случав совпадения w
с центром спектральной линии.
- 237 -
действия амплитудной динамической решетки является изменение с глубиной отношения j-1(z)/j1(z), определяемого формулой
|
j-1(z) |
= |
j-1(0) |
· |
1 + bj1(0) |
(12) |
|
j1(z) |
j1(0) |
1 + bj1(z) |
В усиливающих средах отношение (12) убывает, что соответствует подавлению усиления слабой волны. В средах с поглощением это отношение растет, увеличиваясь в пределе при z®
¥
в 1+bj1(0) раз, однако амплитуда слабой волны c-1(z) не усиливается ни при каких значениях b и j1(z). Проведенное рассмотрение показывает, что использование амплитудных объемных динамических голограмм с записью в поглощающих и усиливающих средах не позволяет достигнуть эффективного преобразования световых пучков.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

