|
|
 |
 |

|
| |
ЭЛЕМЕНТЫ ОБЩЕЙ ТЕОРИИ ДИНАМИЧЕСКИХ ФАЗОВЫХ ГОЛОГРАММ
Л.Е.Чирков
Построены интегральные операторы, которые описывают последовательное накопление изменений световой волны, распространяющейся в среде с модулированными параметрами. Получено общее решение и дана его интерпретация на основе модели фотон-фононного взаимодействия. Определены условия перехода к предельным случаям плоской и объемной дифракционным фазовым решеткам, а также к решениям в приближении слабых управляющих волн. Сформулированы критерии применимости предельных решений.
Динамические фазовые голограммы представляются интересным и практически важным объектом исследования. Они во многих отношениях отличаются от квазидинамических голограмм последовательности, сменяющих друг друга через определенные интервалы времени статических голограмм. В настоящее время только акустооптическое взаимодействие является практически реализуемым способом создания динамической фазовой структуры, подобной фазовой голограмме. Поэтому в дальнейшем изложение вопросов теории динамических фазовых голограмм удобно вести, ориентируясь прежде всего на акустическое взаимодействие.
В работе /1/ мною, совместно с В.Н.Парыгиным, предложен новый метод построения общего решения задачи дифракции света на распределенных фазовых структурах. Отличительная особенность этого метода - предельно широкая формулировка задачи. Здесь будут изложены основные результаты исследования общих решений, касающихся прежде всего вопросов акустооптического взаимодействия динамических голограмм. Однако, при определенных условиях эти результаты
- 213 -
могут быть перенесены и на статические голограммы.
Световой поток и управляющую звуковую волну представим с помощью следующих интегральных преобразований:
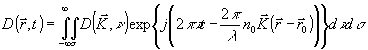 (1) (1)
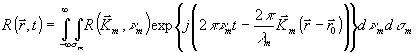 (2) (2)
где u
, l , 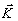 - соответственно частота, длина волны, единичный
волновой вектор световой волны, l =с/u
, с
- скорость света в вакууме, соответствующие
величины, отмеченные индексом "m",
относятся к управляющей волне, n0
- коэффициент преломления среды, d(
- соответственно частота, длина волны, единичный
волновой вектор световой волны, l =с/u
, с
- скорость света в вакууме, соответствующие
величины, отмеченные индексом "m",
относятся к управляющей волне, n0
- коэффициент преломления среды, d(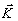 ,u
) и r( ,u
) и r(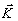 m,u
m) - трехмерные спектральные функции
световой волны и управляющего поля, причем функция
r( m,u
m) - трехмерные спектральные функции
световой волны и управляющего поля, причем функция
r(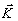 m,u
m) должна быть определена так, чтобы
зависимость коэффициента преломления от звуковой волны была представлена формулой m,u
m) должна быть определена так, чтобы
зависимость коэффициента преломления от звуковой волны была представлена формулой
n(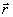 ,t) = n0
+ D nr( ,t) = n0
+ D nr(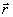 ,t) (3) ,t) (3)
где D n
- амплитуда изменений n(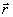 ,t),
D n пропорциональна ,t),
D n пропорциональна
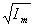 , где im
— интенсивность звука.
, где im
— интенсивность звука.
Интегральные преобразования
(1) и (2)
не являются преобразованиями Фурье. Области интегрирования
s и s
m -
это поверхности второго порядка, описываемые уравнением 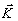 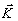 = 1. Когда волновые векторы
= 1. Когда волновые векторы 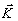 - действительные векторы, поверхности
s и
s m
являются поверхностями шара, радиус которого равен единице. Однако наряду с
действительными векторами уравнению
- действительные векторы, поверхности
s и
s m
являются поверхностями шара, радиус которого равен единице. Однако наряду с
действительными векторами уравнению 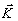 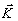 = 1 могут удовлетворять и комплексные векторы,
поэтому в общем случае поверхностями интегрирования являются комплексные шары.
Можно показать, однако, что во всех практически важных случаях неоднородными
волнами, связанными с комплексными векторами
= 1 могут удовлетворять и комплексные векторы,
поэтому в общем случае поверхностями интегрирования являются комплексные шары.
Можно показать, однако, что во всех практически важных случаях неоднородными
волнами, связанными с комплексными векторами 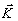 ,
можно пренебречь. ,
можно пренебречь.
Выбор интегральных преобразований (1) и (2) определяется тем, что они представляют общее решение соответствующих волновых уравнений для полуограниченной, однородной, не имеющей источников
- 214 -
среды. В тех случаях, когда рассматриваемые ниже решения применяются к статическим фазовым голограммам, ограничения, накладываемые волновым уравнением на интегральное преобразование (2), могут быть сняты. В этом случае (2) должна быть записана с помощью интеграла Фурье.
Выделим в зоне взаимодействия тонкий слой, расположенный между
плоскостями 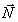 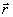 i
= xi и i
= xi и 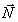 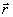 i+1
= xi+1, где
- i+1
= xi+1, где
- 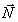 нормаль к плоскостям, ограничивающим зону взаимодействия,
нормаль к плоскостям, ограничивающим зону взаимодействия,
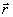 -
радиус-вектор, xi, xi+1
- координаты вдоль нормали -
радиус-вектор, xi, xi+1
- координаты вдоль нормали
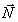 .
Первый этап построения решения состоит в определении интегрального оператора,
который связывает спектральную функцию di( .
Первый этап построения решения состоит в определении интегрального оператора,
который связывает спектральную функцию di(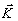 ,u
) световой волны, падающей на слой, с функцией
di+1( ,u
) световой волны, падающей на слой, с функцией
di+1(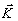 ,u
)световой волны,
выходящей из слоя. ,u
)световой волны,
выходящей из слоя.
При построении оператора тонкого слоя воспользуемся первым приближением к решению задачи дифракции. Этим приближением, как известно, является приближение чисто фазовой модуляции.
Функцию di(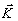 ,u
) рассматриваем как заданную. Подставив ее
в интеграл (1),
определим функцию di( ,u
) рассматриваем как заданную. Подставив ее
в интеграл (1),
определим функцию di(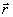 ,t).
Приближение фазовой модуляции позволяет заменить коэффициент преломления n0
в (1) его
возмущенным значением, определяемым формулой
(3). Функцию
di+1( ,t).
Приближение фазовой модуляции позволяет заменить коэффициент преломления n0
в (1) его
возмущенным значением, определяемым формулой
(3). Функцию
di+1(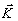 ,u
) - спектральную функцию световой волны, выходящей
из i-ого слоя,
вычислим следующим образом: ,u
) - спектральную функцию световой волны, выходящей
из i-ого слоя,
вычислим следующим образом:
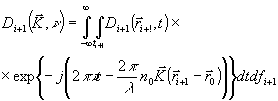 (4) (4)
где ¦
i+1 - поверхность плоскости;
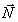 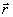 i+1
= xi+1. i+1
= xi+1.
Рассматривая функцию di(t,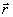 ),
заметим, что под знаком экспоненты (интеграл
(1)) находится функция
D nD xr( ),
заметим, что под знаком экспоненты (интеграл
(1)) находится функция
D nD xr(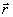 ,t)·2p
/l , (где D
х - толщина
слоя), которая появляется в результате подстановки
(3) в (1). ,t)·2p
/l , (где D
х - толщина
слоя), которая появляется в результате подстановки
(3) в (1).
В дальнейшем мы должны будем совершить предельный переход к точному решению при D
х ®
0. Последнее позволяет уже сейчас рассматривать D
х как величину малую и разложить экспоненту, содержащую D
х, в ряд, сохранив при этом только три первые члена
- 215 -
разложения. При выполнении указанных действий необходимо представить
косинус, входящий в состав спектральной функции
r(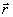 ,t) (2), суммой
двух экспонент. ,t) (2), суммой
двух экспонент.
После всех перечисленных выкладок найдем:
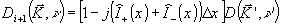 (5) (5)
Линейные интегральные операторы
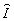 +(х)
и +(х)
и 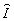 -(х)
равны: -(х)
равны:
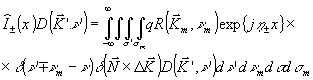 (6) (6)
где
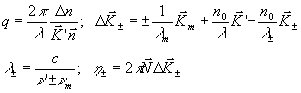 (7) (7)
Общее решение задачи следует искать как произведение операторов
(5) отдельных слоев, на которые разобьем всю
зону взаимодействия. В полученном произведении операторов затем необходимо перейти
к пределу при стремлении к нулю толщины слоев. Если функция, описывающая коэффициент
преломления, не имеет точек разрыва, а вое спектральные функции
di(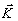 ,u
) определены на полусфере ,u
) определены на полусфере 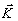 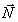 > 0, то предел произведения операторов тонких
слоев существует и он сходится к точному решению задачи.
> 0, то предел произведения операторов тонких
слоев существует и он сходится к точному решению задачи.
Несмотря на очевидную громоздкость рассмотренной схемы ее удается довести до конца и получить решение в виде рядов, составленных из итераций двух операторов Ĉ+(х) и Ĉ-(х) /1/. Операторы Ĉ+(х) определяются соотношением:
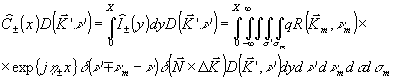 (8) (8)
- 216 -
Общее решение d(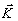 ,u
), представляющее спектральную функцию выходящей
волны, ищется в виде интегрального соотношения ,u
), представляющее спектральную функцию выходящей
волны, ищется в виде интегрального соотношения
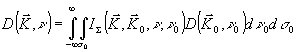 (9) (9)
причем функция iå
представлена рядом
iå
= å
(-j)fp (10)
Функции fp описывают соответствующие дифракционные максимумы /1/. При р > 0 функция fp равна
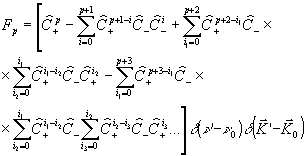 (11) (11)
При р < 0 функция fp равна
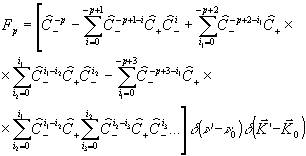 (12) (12)
- 217 -
Удобным инструментом анализа общего решения, которое кокет быть сформулировано на основе рассмотренной схеиы, является дебаевская модель фотон-фононного взаимодействия. Следует отметить, что эта модель, физически оправданная при описании дифракции света на ультразвуке, в случае статических фазовых голограмм может рассматриваться только как полезная аналогия. В этом случае фононы следует рассматривать как виртуальные частицы.
В процессе взаимодействия света с фазовой структурой состояние фотонов изменяется, причем в рамках подали фотон-фононного взаимодействия функция состояния фотонов описывает систему уравнений. Фотоны, находящиеся на различных уровнях, в общем обладают различными энергиями (частотами)
u
p = u
0 + pu
m (13)
и импульсами, которые удовлетворяют уравнению
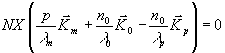 (14) (14)
где р - номер соответствующего уровня (дифракционного максимума). Длина волны l
р равна:
l
p = c/(u
0 + pu
m) (15)
В статическом приближении зависимость от времени отсутствует, поэтому состояния фотонов различаются только по направлениям (1), при этом u
p = u
0 и l
р = l
0.
Процесс дифракционного рассеяния фотонов следует интерпретировать как переходы между рассмотренными уровнями. Разрешенными
- 218 -
переходами при этом являются переходы между соседними максимумами, индекс р в процессе этих переходов может измениться только на единицу. Если индекс р увеличивается, то переход описывается оператором Ĉр(х), если уменьшается - оператором Ĉ-(х). Запрещенными являются все переходы, в которых индекс р изменяется более, чем на 1.
Первоначально вся энергия светового потока сосредоточена в нулевом максимуме и лишь последовательно, минуя все промежуточные уровни, фотон может появиться на р-ом уровне. Переходы между далеко отстоящими максимумами возможны только как многократные переходы. Существует неограниченный набор возможных путей переходов между максимумами.
Кратчайшим путем перехода между нулевым и р-ым максимумом является переход, совершаемый по схеме 0®
1®
2®
... ®
р-1 ®
р, где для определенности считаем р положительным числом. Этот переход описывается оператором Ĉ+р Р. Например, кратчайшим переходом между нулевым и третьим максимумами является переход 0 ®
1 ®
2 ®
3, описываемый оператором Ĉ+3. Кратчайший переход на р-ый уровень описывается оператором Ĉ-р. Следующими по кратности переходами являются переходы с однократным рассеянием в обратном направлении, например в i-м максимуме. Такой переход описывается оператором Ĉ+р+1-iĈ -Ĉ +i (второй член в формуле (11)) или для отрицательного максимума Ĉ—p+1-iĈ +Ĉ -i (второй член в формуле (12)). Например, в третий максимум фотон может попасть по пути 0®
1 ®
2 ®
1 ®
2 ®
3, испытав во втором максимуме переход в обратном направлении (переход 2 ®
1).
Общее число переходов с однократным рассеянием в обратном направлении равно р+2 -м. Оно равно числу всех возможных положений индекса i, указывающего место обратного перехода. Например, для перехода между нулевым и третьим максимумом получим
Ĉ+4Ĉ- + Ĉ+3Ĉ-Ĉ+ + Ĉ+2Ĉ-Ĉ+2 + Ĉ+Ĉ-Ĉ+3 + Ĉ-Ĉ+4
Переходы с кратностью р +4 являются переходами с двухкратным рассеянием фотонов в обратном направлении в максимумах i1 и i2 (третьи члены в формулах (11) и (12)).
- 219 -
Полная суперпозиция таких переходов равна:
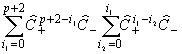
Переставив индексы "+" и "-", получим соответствующее выражение для р-ого максимума. Кроме рассмотренных переходов между нулевым и р-ым максимумами возможны переходы с рассеянием в i1,i2,i3 максимумах - трехкратным рассеянием в обратном направлении; далее следует рассмотреть переходы с четырехкратным рассеянием в обратном направлении, пятикратном и т.д. По всем индексам i, i1, i2,... необходимо выполнить суммирование. Общее решение (10), (11), (12) содержит полную суперпозицию всех возможных переходов.
Различные пути многократных переходов имеют различную вероятность. В частности, вероятность кратчайшего перехода между нулевым и р-ым максимумами Рр не превышает
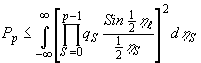 (16) (16)
где ℓ - ширина зоны взаимодействия, a qp пропорциональна im/ℓ, где im — интенсивность звука, или в соответствии с формулой (17)
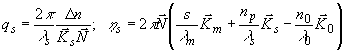 (17) (17)
Аналогичные выражения можно получить и для остальных типов переходов.
Основываясь на выражении (16), можно оценить, какие к переходов вносят существенный вклад в дифракцию, и в дальнейшем учитывать только эти переходы.
В общем виде решение, которое может быть найдено рассматриваемым способом, громоздко, однако, его удается существенно упростить в некоторых частных случаях, среди которых особую роль играют три: дифракция на тонких (плоских) фазовых структурах (дифракция Рамана-Ната), объемное взаимодействие (дифракция Брэгга), дифракция в приближении слабых управляющих волн. Анализируя общее решение,
- 220 -
можно указать условия, при которых оно сходится к одному из перечисленных приближенных решений, достаточно подробно исследованных к настоящему времени.
Особую роль при определении характера решений играет коэффициент h
s (17). В тех случаях, когда частота пространственной несущей удовлетворяет неравенству 1/l
m<<1/l
, а угол падения j
светового луча на фазовую решетку невелик, для оценки h
p удобно использовать приближенное выражение:
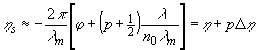 (18) (18)
Можно показать, что если в (18) пренебречь членами, зависящими от р, т.е. считать h
p = h
, то общее решение в случае плоских взаимодействую! волн сходится к бесселевскому распределению:
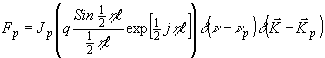 (19) (19)
Известному решению в приближении Рамана-Ната соответствует случай h
= 0. Решение, близкое к (19), получено Рытовым /2/.
Пока р удовлетворяет неравенству
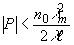 (20) (20)
фаза |
p|
D
h
ℓ < p
. При таких значениях фазы замена h
р на h
в формуле (16) допустима, поскольку она незначительно отражается на величине рассчитанного значения вероятности р-кратного перехода. При больших значениях р зависимость h
р от р становится существенной. Поэтому при описании дифракционных максимумов, номера которых не удовлетворяют неравенству (20), бесселевское распределение неприемлемо.
Неравенство (20) определяет границы применимости дифракции Рамана-Ната, т.е. приближения плоской зоны взаимодействия. С ростом ℓ в соответствии с (20) уменьшается число максимумов, к которым применимо решение (19). Когда ширина зоны взаимодействия
- 221 -
становится достаточно большой,
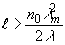 (21) (21)
решение (19) вообще становится неприемлемым даже для самых грубых оценок. Следует отметить, что до сих пор нет приемлемых решений, позволяющих описать дифракцию в промежуточной области, когда ширина зоны взаимодействия достаточно велика (21), чтобы ее нельзя было считать плоской, но и не достигла тех размеров, при которых дифракция становится объемной. Общие решения (11), (12) позволяют проанализировать поведение функций fp в промежуточной области.
Переход к объемной дифракции (дифракции Брэгга) связан, как известно, с предельный' переходом ℓ ®
¥
. В последнем случае вероятность Рр переходит в следующее выражение:
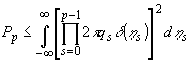 (22) (22)
где d
(h
s) - дельта-функция. Для того, чтобы вероятность перехода между нулевым и р-ым максимумом не была равна 0, необходимо, чтобы все h
s (s = 0,1,2,... р-1) одновременно не были равны нулю. Как видно из (18), выбирая угол падения световой волны j
, можно одно из h
s сделать равной 0. Но только одно! Поэтому при ℓ ®
¥
отличная от нуля вероятность перехода Рp может быть получена (путем соответствующего выбора j
) только в случае р = +1, -1. Условием существования дифракции при ℓ ®
¥
является условие:
h
0,-1 = 0 (23)
Рассмотренные выше примеры перехода к предельным решениям показывают, какую важную роль при этом играет коэффициент h
p. Величина этого коэффициента, в частности, является определяющей при установлении условий перехода к предельным решениям. Рассматривая (17), можно заметить, что коэффициент h
р равен модулю суммарного импульса трех взаимодействующих частиц: фотона, взаимодействующего
- 222 -
с ним фотона и фотона, перешедшего на новый уровень.
В известных решениях, полученных, например, методом связанных волн /3-6/ принято считать суммарный импульс равным нулю.
В этом методе решение ищется в виде системы связанных волн, причем волновые векторы парциальных волк определяются соотношением (используются принятые здесь обозначения):
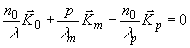 (24) (24)
Сравнивая (24)
и (14),легко
заметить, что эти соотношения определяют в общем разные направления 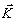 р
(правда эти различия почти во всех, практически
интересных случаях, невелики). Наиболее заметными оказываются различия в определении
фазы дифрагировавших волн. Эти отличия существенные, когда анализируется работа
устройств, в которых осуществляется интерференция волн, дифрагировавших в различные
максимумы. р
(правда эти различия почти во всех, практически
интересных случаях, невелики). Наиболее заметными оказываются различия в определении
фазы дифрагировавших волн. Эти отличия существенные, когда анализируется работа
устройств, в которых осуществляется интерференция волн, дифрагировавших в различные
максимумы.
Если (24)
рассматривать как уравнение относительно единичного вектора 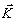 р р,
можно заметить, что оно разрешимо только при определенных значениях длины волны
l р.
Однако, физически нельзя согласиться с тем, что выбор l
р диктуется уравнением (24),
выражающим закон сохранения импульсов. Длина волны l
р связана с частотой фотона u р
формулой (15),
причем u p
определяется из закона сохранения энергии (13).
Поэтому длина волны l р должна устанавливаться
независимо от закона сохранения импульсов, чему противоречит
(24). Указанное противоречие снимается, если
при определении 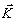 р р
пользоваться уравнением (14).
Наиболее интересным с позиций голографии следует признать решение, отыскиваемое в приближении слабых управляющих волн (малой глубины фазовой модуляции). В этом приближении параметр qℓ, который определяет глубину фазовой модуляции, следует считать малым. Поскольку вероятность р-кратных переходов (22) пропорциональна (qℓ)p, при малых qℓ можно пренебречь всеми переходами, кратность которых выше 1. Поэтому в приближении слабых управляющих волн решениями задачи будут:
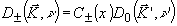 (25) (25)
- 223 -
В дальнейшем для определенности будем рассматривать только +1-ый максимум. Соответствующие решения для -1-ого максимума могут быть получены путем смены индексов.
Выражение (25) можно упростить в случае, когда световая и звуковая волны являются слабо расходящимися. Введем обозначения:
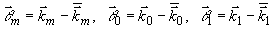 (26) (26)
Векторы 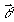 описывают соответствующие отклонения векторов к от их средних значений
описывают соответствующие отклонения векторов к от их средних значений 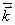 . .
Фиксируем на плоскости, ортогональной 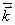 ,
систему координат, определив ее с помощью базисных векторов ,
систему координат, определив ее с помощью базисных векторов 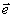 1
и 1
и 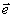 2. 2.
Воспользуемся формулами (8),
(25), (26). Используя приближение слабой расходимости,
перейдем от интегрирования по поверхности шара к интегрированию на поверхности
плоскостей 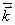 0
и 0
и 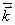 m.
После некоторых выкладок получим m.
После некоторых выкладок получим
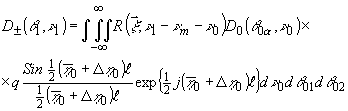 (27) (27)
где q
0a = 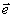 a
q 0, коэффициент a
q 0, коэффициент
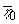 рассчитан по формуле (17)
для средних значений
рассчитан по формуле (17)
для средних значений 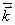 m, m,
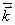 0, 0, 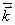 1. 1.
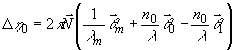 (28) (28)
где q 1a
= 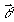 a a
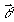 1 1.
Под знаком интеграла (27) стоит произведение трех спектральных функций. Первые две определены выше и описывают, соответственно,
- 224 -
управляющую волну и световой поток. Третья функция описывает дифракционный максимум. Основные решения в приближении плоских зон взаимодействия и объемной дифракции могут быть получены в (27) при замене функции дифракционного максимума константой при ℓ ®
0 и дельта-функцией при ℓ ®
¥
.
Приближение слабой расходимости взаимодействующих волн, основываясь на которой мы перешли от общего выражения (25) к интегралу (27), не всегда практически оправдано. С другой стороны, попытки анализировать непосредственно (25) сопряжены с серьезными математическими трудностями. Этих трудностей удается избежать, если, используя теорему выборок, представить световое поле и звуковую волну суперпозицией конечного' числа плоских волн, определяемых с помощью отсчетов.
На основании теоремы выборок трехмерную спектральную функцию
d(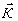 ,u
) представим рядом ,u
) представим рядом
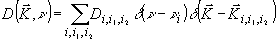 (30) (30)
где 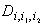 - отсчеты светового поля
d(
- отсчеты светового поля
d(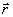 0,t0),
заданного на некоторой плоскости, например 0,t0),
заданного на некоторой плоскости, например 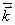 0 0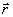 0
= x0. 0
= x0.
 (31) (31)
В (31) использованы следующие обозначения:
u
i = i/t
у 1,
у2 -
координаты в системе координат, определяемой векторами 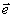 1
и 1
и 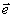 2,
время Т -
длительность светового импульса. 2,
время Т -
длительность светового импульса.
Прямоугольная область интегрирования выбрана так, чтобы прямоугольник имел минимальные размеры и целиком включал всю область локализации луча. Индексы i, i1, i2 принимают как положительные,
- 225 -
так и отрицательные значения.
Волновые векторы 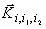 ,
плоских волн, образующих волну, информационно эквивалентную исходной, удовлетворяют
следующему уравнению: ,
плоских волн, образующих волну, информационно эквивалентную исходной, удовлетворяют
следующему уравнению:
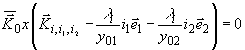 (32) (32)
Аналогичным образом ультразвуковая волна, информационно-эквивалентная управляющей, может быть представлена
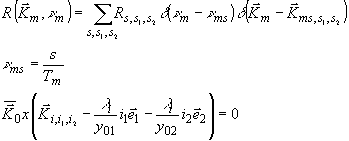 (33) (33)
Отсчеты звуковой волны 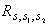 вычисляются с помощью интеграла, аналогичного
(31).
вычисляются с помощью интеграла, аналогичного
(31).
Подставим (30) и (33) в решение (25) и воспользуемся формулой (8), определяющей оператор Ĉ+(x). После некоторых промежуточных выкладок получим следующее решение:
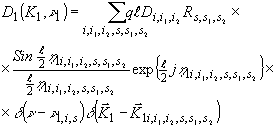 (34) (34)
u
1i,s = u
0 + u
i + u
m + u
ms = u
0 + u
m + i/t + s/tm (35)
- 226 -
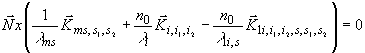 (36) (36)
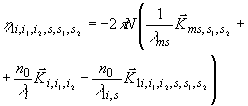 (37) (37)
Отсчеты частот u ms
и u i
входят в (35)
и, следовательно, в решение (34)
линейно, в то время как отсчеты волновых векторов воспроизводятся более сложным
образом. Из решения (34)
следует, что в общем случае искажаются как амплитуда, так и фаза сигналов. Эти
искажения, в
общем, несущественны для тех отсчетов волнового вектора
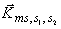 . Для
которых выполнено неравенство . Для
которых выполнено неравенство
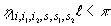 (38) (38)
Несмотря на то, что решение (34) выглядит громоздко, оно сводит задачу исследования решения к анализу числовых соотношений, устанавливаемых формулами (34)¸
(37). Исследуя решение (34) и неравенство (38), можно показать, что положение границ брэгговской дифракции определяется неравенством
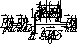 (39) (39)
где sполн
- полное число отсчетов s2
волнового вектора 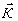 m
ультразвукового поля. Приближение слабых управляющих волн является наиболее
грубым приближением, описывающий процесс восстановления изображений считывающим
световым потоком. Поэтому возникает вопрос, насколько точно это приближение
соответствует реально наблюдаемым процессам. Используя общее решение.можно
найти решения более высокого порядка приближения. В частности, для +1-ого максимума m
ультразвукового поля. Приближение слабых управляющих волн является наиболее
грубым приближением, описывающий процесс восстановления изображений считывающим
световым потоком. Поэтому возникает вопрос, насколько точно это приближение
соответствует реально наблюдаемым процессам. Используя общее решение.можно
найти решения более высокого порядка приближения. В частности, для +1-ого максимума
- 227 -
вторым приближением является решение
d1(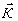 ,u
) = [Ĉ+ + Ĉ+Ĉ-Ĉ+
+ Ĉ-Ĉ+Ĉ+ +
Ĉ+Ĉ+Ĉ-]d0(k',u
') (40) ,u
) = [Ĉ+ + Ĉ+Ĉ-Ĉ+
+ Ĉ-Ĉ+Ĉ+ +
Ĉ+Ĉ+Ĉ-]d0(k',u
') (40)
Можно выписать еще более точные решения.
Не останавливаясь на деталях анализа, отметим, что с ростом глубины фазовой модуляции, когда вклад в решение дают члены более высокого порядка, чем однократный переход, наряду с увеличением яркости изображения идет процесс его разрушения. В случае плоских зон взаимодействия на восстановленное изображение будут накладываться функции автокорреляции трехмерных спектральных функций управляющей волны, причем ее амплитуда пропорциональна (qℓ)3. Дальнейший рост глубины фазовой модуляции приводит к увеличению вклада в решение пятикратных переходов. Влияние многократных переходов приводит к появлению нелинейных членов в амплитудно-частотной характеристике.
Аналогичные эффекты характерны и для объемной дифракции. Многократные переходы в этом случае приводят к появлению в решении членов, пропорциональных степеням трехмерной спектральной функции управляющей волны.
Влияние нелинейных членов, связанных с многократными переходами, тем выше, чем больше глубина фазовых переходов потому, если на принято специальных мер по ограничению или компенсации нелинейных членов, следует рекомендовать режим слабых управляющих волн.
Литература
1. В.Н.Парыгин, Л.Е.Чирков. Радиотехника и электроника, Хviii, 4, 703, 1973.
2. С.М.Рытов. Изв. АН СССР, сер. физич., 2, 222, 1937.
3. Е.Р.Мустель, В.Н.Парыгин. методы модуляции и сканирования света, Москва. 1970.
4. Н.М.Померанцев. Квантовая электроника, 5(11), 118 и 122, 1972.
5. w.r.klein, В.d.cook. ieee trans., su-14, 3, 123, 1967.
6. h.kogelnik. bell syst.techn.j., 48, 9, 2909, 1969.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

