Явление интерференции света широко используется в оптических приборах. С появлением и развитием голографии - нового метода получения изображений предметов и преобразования информации, переносимой световыми волнами, - подход к явлению интерференции света существенно изменился. Так, например, появилась возможность вызывать интерференцию волн, разнесенных во времени и в пространстве, при помощи наложения волновых полей в скрытом голографическом изображении. Другое направление в оптике, которое возникло благодаря голографии, - это методы регистрации затухающих волн и преобразования информации, сосредоточенной в области сверхвысоких пространственных частот. Изложение последних достижений в этой области составляет тему данной работы.

Основные черты процесса интерференции световых волн можно уяснить на примере интерференции двух плоских волн света, одна из которых характеризуется частотой ω₁=2πν₁ и волновым вектором k₁, а вторая - частотой ω₂=2πν₂ и волновым вектором k₂. Амплитуда суммарного поля в области пересечения этих двух плоских

где х(х,у,z) - вектор точки наблюдения о координатами х, у, z; k(k_x ,k_y, k_z) - волновой вектор о компонентами k_x ,k_y, k_z, a t - время.

Распределение интенсивности cвета в области пересечения двух плоских волн определяется выражением

где Δω=ω₁-ω₂ - частота биения поля, а κ=k₁-k₂.

где (8)

1. Обе волны света имеют одинаковые частота. Здесь Δω=ω₁-ω₂=0 . Интерференционная картина неподвижна в пространстве. Ее можно зарегистрировать в виде традиционной голограммы.

2. Волны имеют различные частоты и различные волновые векторы. Здесь ω₁≠ω₂, k₁≠k₂. Интерференционная картина бежит в пространстве со скоростью v, определяемой выражением (7).

3. Волны имеют одинаковые частоты, но разные волновые числа. Здесь ω₁≠ω₂, k₁≠k₂, Δω=0. Это возможно только при интерференции затухающих волн. Несмотря на то, что волновые числа различны, интерференционная картина неподвижна в пространстве, и ее можно зарегистрировать с помощью голограммы. О том, как это сделать, подробно описывается в лекции.

а) волновые векторы k₁ и k₂ - антипараллельны. Здесь Δk≃2k₀, а k0=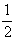(k₁+k₂), скорость движения интерференционной картины равна

б) волновые векторы k₁ и k₂ параллельны друг другу. Здесь Δk≃, а скорость движения интерференционной картины

в) случай, когда вектор κ=k₁-k₂ перпендикулярен вектору k₁. Здесь κ=k₁tgθ, , а (рис.2в).

Рис.2. Частные cлучаи интерференции плоских волн разных частот и разных волновых векторов:

а) волновые векторы k₁ и k₂ - антипараллельны;

б) волновые векторы k₁ и k₂ - перпендикулярны;

в) вектор κ перпендикулярен вектору k₁;

г) случай, когда Δk= k₁-k₂ << | k₁ - k₂|.

г) случай, когда Δk= k₁-k₂ << |κ|. Здесь

д) случай, когда волновые векторы k₁ и k₂ взаимно параллельны. Скорости

Интерференционная картина движется в пространстве со скоростью света. В явном виде распределение интенсивности света в интерференционной картине этого типа равно:

Рассмотрим процесс возникновения затухающих волн при полном внутреннем отражении света. Если плоская монохроматическая волна падает на плоскую границу раздела двух сред с показателями преломления n₁ и n₂ n₁>n₂, то в области углов падения волны в среде /1/ φ, οревышающих критичеокий угол полного отражения

возникает явление полного внутреннего отражения. Чтобы описать его, возьмем систему прямоугольных координат x, y, z так, чтобы плоскость хоу совпадала с плоскостью раздела сред, а плоскость уoz являлась плоскостью падения (рис.3). Пусть электрический вектор линейно-поляризованного света имеет только х-компоненту /2/.

Здесь λ₀, λ₁ и λ₂. Длина волны света в свободном пространстве, в среде (1) и в среде (2), соответственно.

Если φ₁>φ_крит, то sinφ₂>1 и

Из (15) и (16) видно, что волновое поле в среде (2) всегда распространявтоя вдоль границы раздела сред и волновой вектор k_z имеет только у-компоненту. Амплитуда поля в среде (2) ослабевает на длинах z₀, соизмеримых с длиной волны света. Это - затухающая волна. Ее интенсивность, равная

в поверхностном олое достаточно велика. Так, например, для φ₁=φ_крит интенсивность затухающей волны в 4 раза больше интенсивности падающей волны.

Наиболее существенным свойством затухающих волн является то, что длина волны λ_s затухающих волн так же, как и волновое число k_s, явным образом зависят от угла падения φ₁ в среде (1), а именно:

Поэтому, варьируя угол падения φ₁, можно изменять длину волны света в среде (2), не изменяя при этом частоту ω₁. С изменением угла φ₁ изменяется также фазовая скорость

где С₁ - фазовая скорость в среде (1). Замечательно при этом то, что длина волны света λ_s и фазовая скорость c_s затухающей волны не зависят от свойств среды (2). Это следствие того, что структура затухающих волн определяется структурой падающей волны. Только декремент затухания z₀ в среде (2) зависит от показателя преломления этой среды. При этом, чем сильнее различие в показателях преломления среды (1) и (2), тем быстрее по глубине затухает волна.

λ₍₁₎<λ_s<λ₍₂₎,

Поскольку показатель преломления в области оптических частот нигде не превосходит n≈3, то самая короткая длина волны затухающих волн, возникающих при полном внутреннем отражении, равна

где ω₀=2π/2, ΰ а - шаг решетки. При освещении дифракционной решетки плоской волной

Если шаг решетки а оказывается меньше длины волны света λ0, (a<λ0), то sinφ>1 и

Из (26) видно, что длина волны затухающей волны света, равная λ_s=a, может принимать произвольно малые значения, в соответствии со структурой дифракционной решетки.

Шаг полос в плоскости z=0 вдоль оси "у" равен

Контраст интерференционной картины экспоненциально затухает с координатой z.

Рассмотрим теперь интерференцию двух затухающих волн. Пусть их частоты ω₁ и ω₂ одинаковы, а волновые числа разные (k₁≠k₂). Если две затухающие волны распространяются в одну и ту же сторону (рис.7а), то амплитуда первой затухающей волны равна

(35а)

Интерференционные полосы ориентированы и затухают в направлении оси z. Шаг интерференционной картины (36) равен

Если , то

Опыты с затухающими волнами /2-4/ полностью подтвердили все предсказания теории. В этих опытах в качестве среды (2) использовалась фотоэмульсия, показатель преломления которой равнялся n₂=1,63 - 1,64 для длины волны света λ = 633 n. Первой средой (1) быка жидкость с большим показателем преломления или стеклянная пластинка из стекла марки флинт. Требованиям химической и физической инертности и легкости удаления с поверхности фотоэмульсии удовлетворяли следующие вещества: дииодометан, n₁ = 1,74 для λ = 633 n и альфа-хлоронафталин, n₁ = 1,63 для λ = 633 n.

Световодами служили призмы из стекла флинт (рис.8, 9) или кювета, заполненная жидкостью n₁ (рис.10). Во всех опытах обнаружено почернение в тонком поверхностном слое фотоэмульсии, которое было вызвано затухающими волнами. Однако, если взять угол

Наиболее интересными оказались опыты по интерференции двух затухающих волн, распространяющихся навстречу друг другу. Эти опыты являются аналогом опыта О.Винера со стоячими волнами /5/.

Шаг интерференционной картины равнялся по расчету В лучах видимого света такую мелкую структуру обнаружить невозможно.

Проанализируем теперь процесс дифракции затухающих волн на плоской решетке с шагом а (рис.11). Пусть затухающая волна k_s с частотой ω распространяется вдоль решетки. Образующиеся при

этом дифрагированные волны имеют ту же частоту, но другую длину волны. Направление распространения дифрагированной волны характеризуется углом φ между нормалью к решетке и волновым вектором дифрагированной волны k. Величина угла φ определяется из условия, чтобы волны, идущие от различных участков дифракционной. решетки, складывались с усилением. Для этого необходимо, чтобы, например, задержка во времени Δt между лучами i и ii (рис.11) равнялась целому числу периодов электромагнитного поля а именно

или

Если |sinφ|≤1 то дифрагированная волна является однород ной волной. Если же |sinφ|≥1, то дифрагированная волна может быть затухающей. Итак, при дифракции затухающей волны на решетке с шагом а<λ, дифрагированная волна может быть как однородной, так и затухающей. Замечательной особенностью процесса дифракции затухающих волн на плоской решетке является то, что в общем случае при дифракции происходит изменение длины волны света.

Уравнение решетки (44), которое описывает дифракцию затухающей волны κ₂ на решетке с образованием дифрагированной волны κ₁, можно обратить в рассматривать это уравнение как описание дифракции водны κ₁ с образованием дифрагированной волны κ₂. Все изложенные случаи процесса дифракции волн на плоской решетке можно свести в следующую таблицу:

№№	Падающая (или дифрагированная) волна κ1	Пространственная частота решетки κa	Дифрагированная (или падающая) волна κ2
1 2 3 4	| κ1|≤ κn	κa ≤ κn	| κ2|≤ κn | κ2|> κn
		κa> κn	| κ2|< κn | κ2|> κn
5 6 7 8	| κ1|> κn	κa ≤ κn	| κ2|≤ κn | κ2|> κn
		κa > κn	| κ2|≤ κn | κ2|> κn

Здесь κ_n=1/λ_n, λ_n - длинa волны в среде с n.

Первые четыре случая соответствуют дифракции однородной волны на дифракционной решетке. В случаях 2 и 4 дифрагированная волна является затухающей. Случаи 5 и 6 соответствуют дифракции затухающих волн на решетке с а≥λ_n, когда могут возникнуть либо однородная волна, либо затухающая волна с измененным значением длины волны. Случай 7 - это дифракция затухающих волн на решетке, шаг которой меньше длины волны света. Здесь могут возникнуть однородные дифрагированные волны. Случай 8 - это дифракция затухающих волн на решетке с шагом a<λ_n. Здесь дифрагированная волна является затухающей той же или измененной длины волны.

на случай затухающих волн. Здесь φ₁ - угол падения, φ₂ - угол дифракции света с длиной волны λ. Если шаг решетки а меньше длины волны λ, а<λ , и если sinφ>1, то при освещении решетки плоской волной дифрагированная волна является затухающей и имеет изменяющуюся с углом φ₁ длину волны. Если же а<λ/2, то при любых углах падения φ возникают только затухающие волны.

Уравнение (49) эквивалентно уравнению (44), если заменить на () и учесть, что φ₂ = 90° для затухающей волны в среде (2).

Свойство i. Можно изменить направление падающей и дифрагированной волны на обратные. Возьмем голограмму, полученную при интерференции затухающей волны 1 с плоской волной 2 (рис.12). Если эту голограмму осветить волной 1, то восстановится волна 2. Если же

эту голограмму осветить затухающей волной 1', идущей навстречу волне 1, то восстановится волна 2', которая распространяется навстречу волне 2. Действительно, когда голограмма освещается волной 1 или 1', то в среде (2) возникает затухающая волна с

Эта затухающая волна дифрагирует на голограмме с пространственной частотой κ_а и в соответствии с уравнением (44) образует дифрагированную однородную волну с κ₂=κ_s+κ_a.

Свойство ii. Изменение длины волны света , возникающей на стадии восстановления, при изменении угла падения φ₁.

Это непосредственно вытекает из уравнения (18). В соответствии с уравнением (48) происходит изменение угла дифракции φ₂.

Свойство iii. Можно заменять предметный пучок на опорный, а

опорный на предметный. Если голограмму осветить волной 2 (рис.12), то восстановится волна 1. Аналогично, при освещении голограммы волной 2 восстановится волна 1. Это свойство можно пояснить так. Освещающая голограмму однородная волна 2 дифрагирует на голограмме с пространственной частотой κ_а. Согласно (48), при этом возникает затухающая волна с длиной волны λ_s=1/κ_a, которая в точности равна длине волны затухающей волны при полном внутреннем отражении волны света, упавшей на плоскость раздела сред под углом φ₁. Поэтому волна 1 выйдет в среду под углом φ₁. Таким образом, голограмма с пространственной частотой κ_а позволяет вывести излучение из оптически менее плотной среды (2) через границу раздела сред в оптически более плотную среду (1) под углом о нормалью в более плотной среде, значение которого превышает критический угол полного внутреннего отражения. При изменении угла падения волны 2 на стадии восстановления происходит изменение угла входа волны 1.

Схема получения голограммы затухающих волн произвольного предмета приведена на рис.13. Опорным пучком здесь является затухающая волна, а предметная волна - однородная волна, рассеянная предметом. Несущая пространственная частота гологрaммы определяется длиной волны затухающей волны

Максимальная и минимальная пространственные частоты голограммы равны

В работе /7/ описан опыт по получению голограммы шахматной доски с использованием в качестве среды (1) дииодометана с показателем преломления n = 1,74 при λ= 633 nm^- и в качестве среды

(2) фотоэмульсии с n₂=1,63. Длина волны затухающей волны, используемой в качестве опорного пучка, равнялась λ_s= 374 nm^-. Таким образом, несущая пространственная частота голограммы равнялась κ_t = 2680 nm^-1 .

Сверхвысокими пространственными частотами будем называть пространственные частоты, которые не могут образовывать однородные волны при нормальном падении на плоскую структуру. Для фотоэмульсии эта пространственная частота равна κ₂=2420mm^-1. Поскольку κ_min=2541mm^-1 > κ₂=2420mm^-1, то при освещении такой голограммы плоской волной при нормальном падении могут образоваться только затухающие волны.

Рис.14. Рисунок, поясняющий стадию восстановления на голограмме, полученной по схеме рис.12. При дифракции затухающих волн на сверхмелкой структуре голограммы полоса пространственных частот κ_min< κ <κ_max переносятся в область низких пространственных частот: Δκ_d=κ_s. При этом ширина полосы пространственных частот не изменяется.

новления. Сверхвысокие пространственные частоты сдвигаются на величину κ_s в процессе дифракции затухающих волн на cверхмелкой пространственной структуре и в результате этого образуется однородная восcтановленная волна, содержащая только низкие пространственные частоты.

Несущая пространственная частота в этом опыте равнялась κ_Т=5360mm^-1.

вительно, κ_t-κ_s = 5360 - 2680 =2680 mm^-1 > κ₂- 2420 mm^-1.

процессе дифракции полоса сверхвысоких частот вокруг κ_Т смещается в область частот (κ_t-κ_s). Эти частоты являются все еще сверхвысокими пространственными частотами, и волны света, отвечающие этим частотам, непосредственно наблюдать невозможно. Только при переходе волны через границу раздела двух сред с n₂>n₁, возникает вторичная однородная волна о низкими пространственными частотами.

С изменением угла падения φ₁ освещающей волны происходит изменение длины волны и волнового числа падающей затухающей волны, используемой на стадии восстановления. При этом спектр пространственных частот предмета перемещается в область других пространственных частот, в результате чего восстановленное изображение появляется в другом месте.

Голограмма затухающих волн представляет особый интерес для достижения "сверхразрешения" в оптически изобрааающих системах. По классическим представлениям, разрешающая способность таких систем определяется как длиной волны освещающего света, так и величиной угловой апертуры входного зрачка. Структурные элементы предмета, которые имеют пространственные частоты больше κ_s=1/λ_s, не могут быть замечены в микроскоп, так как эти структурные элементы создают только затухающие волны, которые не могут участвовать в процессе получения изображения. Однако, этот процесс обратим и если такую структуру светить затухающими волнами с очень малой длиной волны, то при дифракции возникнут однородные волны, которые можно направить в изображающую систему. А поскольку частота электромагнитного поля не изменяется как в процессе превращения затухающей волны в однородную, так и обратном процессе, то изображающая система может работать в видимом диапазоне длин волн. Напомним, что спектральная чувствительность фотоэмульсии определяется частотой электромагнитного поля, а не длиной волны света. Традиционное использование длины волны света, как параметра спектральной чувствительности фотоэмульсии оправдано только тем, что

Поясним теперь принцип работы оптической системы, в которой "сверхразрешение" получается благодаря явлению дифракции затухающих волн /7/. Возьмем в качестве объекта наблюдения плоскую решетку с шагом а. Если а<λ/2, то такую решетку невозможно увидеть, какое бы косое освещение мы не использовали. Осветим решетку затухающей волной с длиной волны λ_s=а, которая распространяется вдоль плоскости решетки. При дифракции возникает однородная волна, которая выйдет из среды под углом φ=0. Эту волну можно направить в апертуру любой оптической изображающей систему. Однако, чтобы сохранить информацию о всех пространственных частотах, необходимо сделать несколько этапов преобразования. Метод получения "сверхразрешения", разработанный и опробованный Г.Нессенштейном, сводится к трем этапам.

κ_s = κ_а-κ_b, (53)

где κ_a - высшая пространственная частота структуры, κ_b -высшая пространственная частота преобразованного спектра.

Третий этап - сдвиг полученного спектра в область высоких пространственных частот на величину κ_s/М. Полученный спектр соответствует увеличенному в М раз изображению предмета (рис.19).

Легко видеть, что этот метод можно использовать только в том случае, если ширина полосы пространственного спектра существенно меньше частот κ_a. В противном случае, сдвинутый на первом этапе спектр пространственных частот будет переходить в область отрицательных пространственных частот, что с неизбежностью приведет

Рис.17. Первый этап метода получения сверхразрешения Г.Нессенштейна с помощью голограммы затухаювих волн. Производится сдвиг спектра из области сверхвысоких пространственных частот в область пространственных частот. При дифракции образуются однородные волны.

Рис.19. Третий этап метода получения сверхразрешения при помощи, голограммы затухающих волн. Производится сдвиг спектра в область высоких пространственных частот на частоту сдвига κ_s/М. При правильном выборе М спектр попадает в область частот, где при дифракции возникают однородные волны.

Схема экспериментальной установки, дащей "сверхразрешение", приведена на рис.20. Объект-решетка 2 помещена в стеклянный сосуд 10, заполненный дииодометаном. Ее изображение переносится на голограмму 4 при помощи оптической системы 3 с линейным увеличением в М раз. Сначала объект-решетка освещается затухающей волной, которая формируется пучком 12. Опорным пучком при получении голограм-

мы является пучок 5. Во время второй экспозиции объект освещается однородной волной ii и опорным пучком 6. Угол ρ₂ выбирается таким образом, чтобы на стадии восстановления с использованием пучка 6 спектр пространственных частот, получающийся при освещении затухающей волной, смещался относительно спектра пространственных, частот при второй экспозиции на величину κ_s/М. Уравнение решетки в случае плоской голограммы дает следующее соотношение:

Установка была испытана на простом примере объект-решетки с шагом а=380 nm , κ_а=2630 mm^-1. При совещании объект-решетки затухающей волной с λ_s=400 nm, κ_s=2500mm^-1 образовывалаоь однородная волна, идущая в направлении

φ=2°43' в ch₂i₂ и 4°43' - в воздухе.

В плоскости изображения оптического проектора а коэффициентом увеличения М=10 угол падения дифрагированных волн равнялся

При интерференции с опорной волной 5, имеющей угол падения ρ'=36°. получалась голограмма с шагом 1,09 μm^-. Спектр нулевого порядка, возникающий при освещении предмета однородной волной, создавала плоская волна с углом падения 0°. Эта волна голографировалась путем интерференции с опорной волной 6, идущей под углом ρ₂=48°15.

Стадия восстановления проводилась с помощью волны 6, которая образовывала одновременно волну нулевого порядка, φ₀=0°, и сдвинутую волну боковой полосы частот под углом φ_s=9°35'. Интерференция этих двух восстановленных волн создавала общее волновое поле, соответствующее увеличенному изображению объект-решетки с шагом

Критерий Рэлея как критерий визуального разрешения, связан с процессом дифракции света. Согласно критерию Рэлея /11/, два изображения равной интенсивности считаются разрешимыми, если интенсивность в седловидной точке составляет 0,811 от максимальной интенсивности. Последнее имеет место тогда, когда главный максимум первого изображения совпадает с первым минимумом другого. Для изображающих систем типа телеокопа критерий разрешения Рэлея определяется величиной

где n - показатель преломления стекла объектива, θ - апертурный угол, коэффициент 0,61 соответствует некогерентному освещение, а 0,77 - когерентному.

Существенный-вклад в теорий разрешающей способности дал Д. Габор, который сформулировал теорему о конечном числе степеней свободы волнового поля, захватываемого оптической системой /12/. Если картина изменяется во времени, то, кроме пространственных степеней свобода, вводят временные степени свободы. Согласно теореме Д.Габора, полное число степеней свободы волнового поля строго ограничено. Поэтому единственно, что может делать экспериментатор - это перераспределять оптимальным образом степени свободы волнового поля. Так, например, ширину полосы передаваемых проотранотвенных частот можно увеличить путем уменьшения ширины полосы передаваемых временных частот или наоборот. В предельном случае, когда ширина полосы передаваемых пространственаых частот отвечает всего лишь одной степени свободы, используют временные частота для пере-

Если же волновое поле стационарно и система наблюдения не обладает временными степенями свободы, то ширина полосы пространственных частот, передаваемая изображающей системой, задается фундаментальным соотношением Рэлея-Габора. Как это не покажется удивительным на первый взгляд, но сверхразрешающая система Г.Нессенштейна не противоречит теореме Габора. Вое дело в том, что главной особенностью системы Г.Нессенштейна является то, что при помощи затухающих волн удается зарегистрировать информацию об объекте в области сверхвысоких пространственных частот, которые ранее были абсолютно недоступны для традиционного микроскопа в лучах удимого света. Таким образом, речь идет о величине пространственных частот и ничего пока что не говорится о ширине полосы частот. А эта величина, как легко доказать, находится в полном соответствии с теоремой Д.Габора. И именно по этой причине для эффективной работа сверхразрешащей системы Г.Нессенштейна приходится производить несколько экспозиций, что эквивалентно использованию временных степеней свободы. В системе Г.Нессенштейна производят когерентное наложение нескольких волновых полей, каждое из которых содержит ограниченную полосу пространственных частот. Это ограничение вытекает из требования, чтобы низшая пространственная частота после первого этапа не попала в область отрицательных пространственных частот. В общем случае число требуемых экспозиций равно

где Δκ_сверх - полная полоса пространственных частот, которую необходимо передать без искажения с помощью сверхразрешающей системы, а Δκ_max - ширина полосы пространственных частот, которая может быть передана изображающей системой согласно теореме Д. Габора.

Метод, разработанный Дж.Строуком, требует очень высокого динамического диапазона регистрирующей среды. Ему удалось получить динамический диапазон в фотоэмульсии, равный 10⁶:1 для линейной передачи по амплитуде света в фильтре с контрастом γ = 2 и 10⁴:1 для линейной передачи по амплитуде в фильтре с контрастом γ= 1. Фотография, полученная в электронном микроскопе с разрешением 5 Å превращалась о помощью фильтра Дж.Строука в изображение, разрешение в котором составляло 2,5 А.

Следует подчеркнуть, что метод апостериорного улучшения качества изображения применим и эффективно работает только в том случае, если при этом устраняются аберрации в изображающей системе. Если же аберрации отсутствуют и оптическая изобрадающая система является совершенной, то метод апостериорной обработки отпадает сам по себе. Действительно, когерентная передаточная функция совершенной изображающей системы равна 1 для всех пространственных частот, передаваемых системой. И поэтому обратный, восстанавливающий фильтр для этой системы также будет равен 1 /14/. Вот здесь то и следует использовать метод сверхразрешения Г.Нессенштейна, хотя он работает только для плоских предметов.

13. g.w.stroke and m.halious. attainment of diffraction-limited imaging in high-resolution electron microscopy bу "a posteriori" holographic Image sharpening 1. optik, 35, 1, 50, 1972.