applications of the most general isoplanatism theorem to holography
w.t.welford
imperial college, london, great britain
the most general isoplanetism theorem /1/ was developed to solve problems in lens optics. isoplanetism is concerned with the concept of stationarity of aberrations with small displacements of the imaging pencils; starting with the optical sine condition of ernst abbe, which applies to the axial region of a symmetrical optical system, we are led to consider off-axis regions, displacements in any direction and eventually optical systems with no symmetry.
holographic Image formation is in principle aberration-free if the reconstructing beam has the same geometry as the reference beam and if the reference and reconstructing wavelengths are the same. if for example the reconstruction geometry is changed then aberrations will be introduced and it is of interest to see whether there are any situations where this does not occur, i.e. isoplanetism geometries.
the problem may be simplified by considering a fresnel hologram of a single point using an unaberrated point source as reference; what happens if the hologram is reconstructed with a displaced point source? a study of this problem /2/ shows that the geometry shown in fig.1 is isoplanatic, where the object and reference points are mirror images in the plane of the hologram. a small displacement of the reconstructing source in any direction produces a mirror Image displacement without aberrations of the reconstructed, Image. it can also easily be shown from first principles that an Image plane hologram is isoplanatic if the axis of rotation which causes the displacement passes through the Image point. a third geometry which is isoplanatic is the fourier transform hologram, in which both the object and reference points are at infinity.
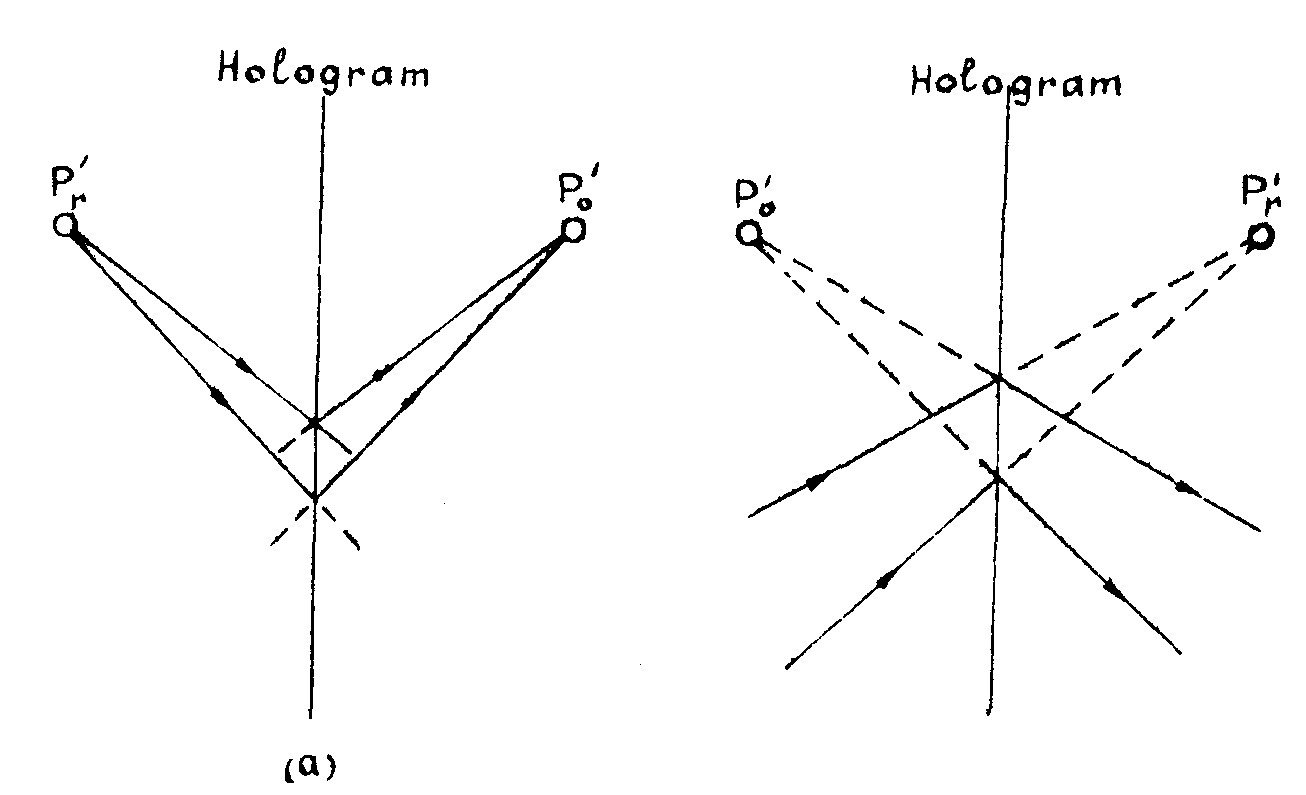
fig.1. geometry of an aplanatic plane hologram; (a) real reference, virtual
object (b) virtual reference, real object. in reconstruction (a) gives a real
Image 
for a real reconstruction
point 
and (b) gives a virtual
Image for a virtual reconstruction
point .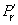
in classical lens optics there are certain well-known refracting and reflecting configurations which are aplanatic and this suggests we should look at holograms on curved surfaces to see if there are corresponding configurations. fig.2 shows the results; if the radius of curvature of the hologram is r and if object and reference points are at distances l0 and lr then a hologram formed according to the condition
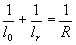(1)
will be aplanatic for displacements transverse to the axis. this suggests a wide range of possibilities for hologram lenses.
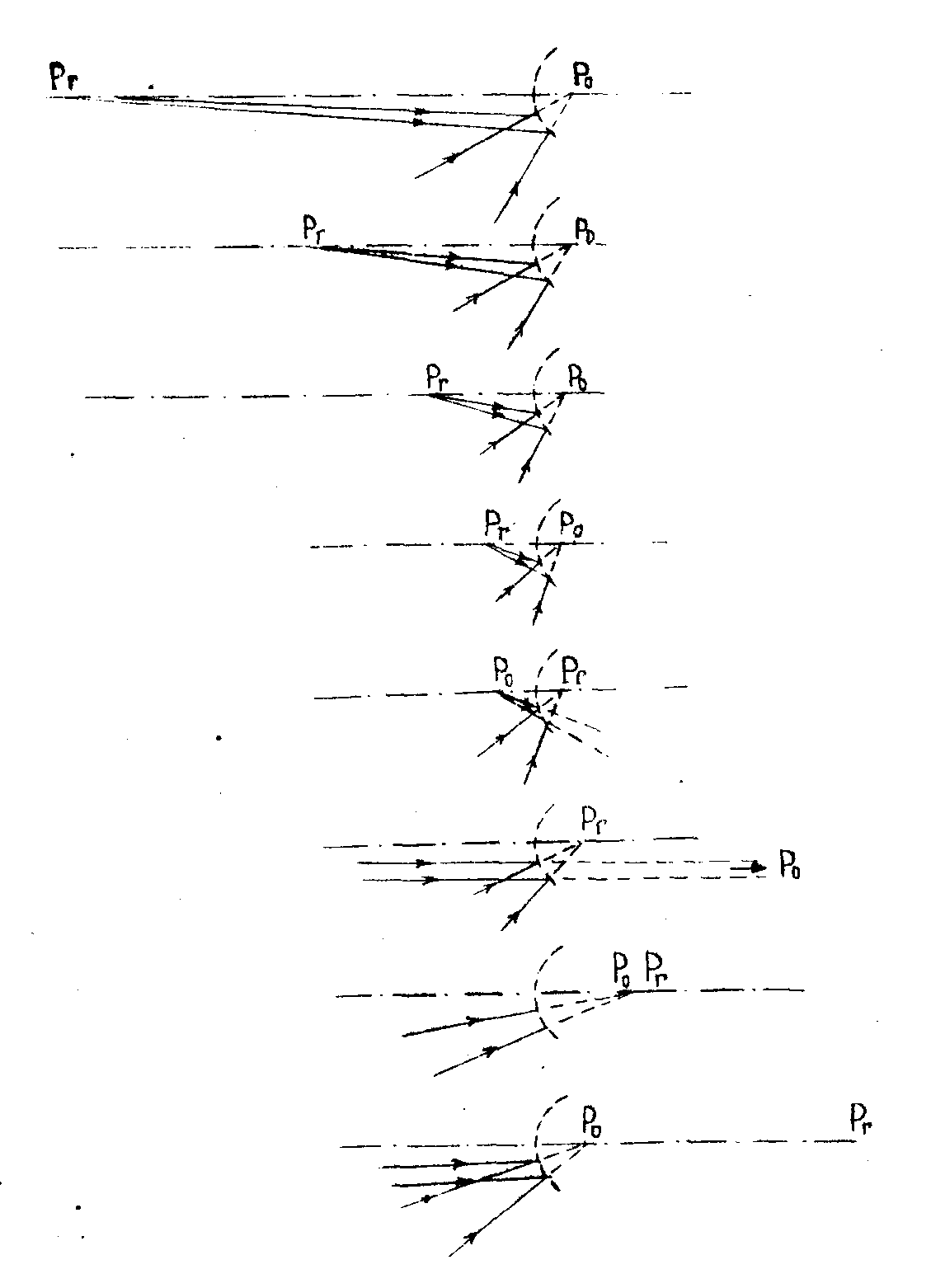
fig.2. reference (pr) and object (p0) points which give an aplanatic hologram on a portion of a sphere, shown in full line, according to eq.(1).
references
1. w.i.welford. optics communications, 3, 1-6, 1971.
2. w.t.welford. optics communications, 8, 239-43, 1973.
