|
|
 |
 |

|
| |
ПРЕОБРАЗОВАНИЕ ГИЛЬБЕРТА И ЕГО ПРИМЕНЕНИЕ В ОПТИКЕ
Л.М.Сороко
Цель работы - продемонстрировать, что интегральное преобразование Гильберта имеет для двухмерных систем считывания и обработки информации такое же значение, как и преобразование Фурье.
Дается определение преобразования Гильберта. Роль преобразования Гильберта в оптике иллюстрируется на ряде примеров. Это - пространственная причинность в когерентных оптических системах, метод визуализации фазовых неоднородностей с помощью ножа Фуко и фазового ножа, свойства дифракционной решетки со сбоем, алгоритм распознавания образов путем одновременного отображения фурье-образов и гильберт-образов входного двухмерного сигнала, а также система наблюдения свойств нематических жидких кристаллов.
1
По определению, преобразованием Гильберта называется переход от исходной функции f (х) к другой функции χ(х), которая равна /1/
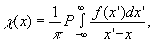 (1) (1)
где интегрирование ведется в смысле главного значения "Р".
 (2) (2)
Функцию χ(х) называют гильберт-образом функции f(х) . Преобразование Гильберта (1) является частным случаем преобразования свертки исходной функции f(x) с ядром g(х). Ядром преобразования Гильберта является функция
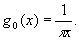 (3) (3)
Поскольку фурье-образ функции g0(х), играющей роль сомножителя свертки в соотношении
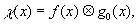 (4) (4)
равен
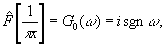 (5) (5)
где знаковая функция
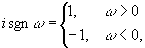 (6) (6)
то преобразование Гильберта обычно осуществляют при помощи фильтра пространственных частот с характеристической функцией g0(ω)(5). Из (5) и (6) видно, что частотный фильтр Гильберта имеет структуру фазовой пластинки, вызывающей разноименные относительно нулевой фазы сдвиги фаз Δφ=±π/2 νа разноименных полуплоскостях в частотной области.
Для двухмерной функции f(x) = f(х,у) сдвиг фаз в четных квадрантах частотной плоскости ω(ωx, ωy) равен -π/2 и +π/2 - в нечетных квадрантах /1/.
Рассмотрим типичные примеры преобразований Гильберта.
1. Исходный сигнал равен синусоиде типа
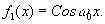 (7) (7)
Ее фурье-образ равен (рис.1):
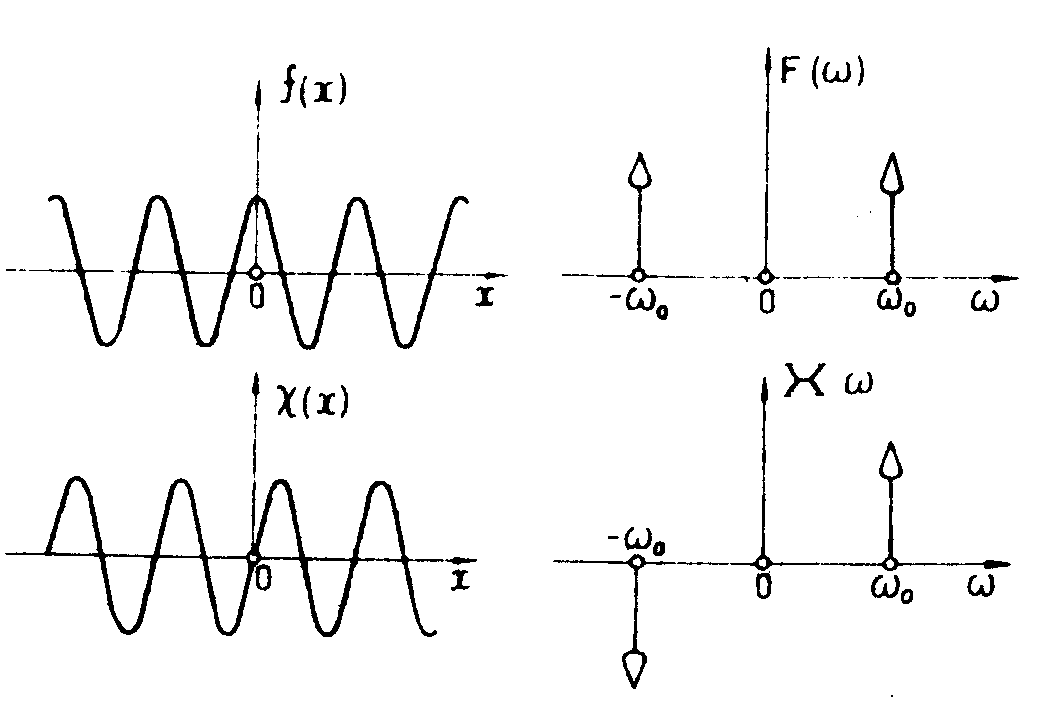
Рис.1. Пример преобразования Гильберта. Исходный сигнал - косинусоида. Гильберт-образ равен синусоиде. Показан Фурье-образ исходного сигнала и результат воздействия на него характеристической функции Гильберта.
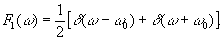 (8) (8)
Фильтр Гильберта (5), (6) превращает его в функцию
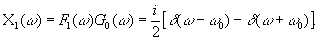 (9) (9)
После обратного преобразования фурье получаем гильберт-образ
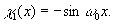 (10) (10)
Таким образом,
 (11) (11)
где оператор 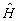 обозначает операцию преобразования Гильберта.
обозначает операцию преобразования Гильберта.
2. Исходный сигнал имеет вид центрированного прямоугольного импульса:
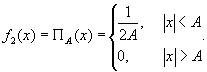 (12) (12)
Прямые вычисления о помощью (1) дают (рис.2)
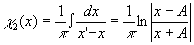 (13) (13)
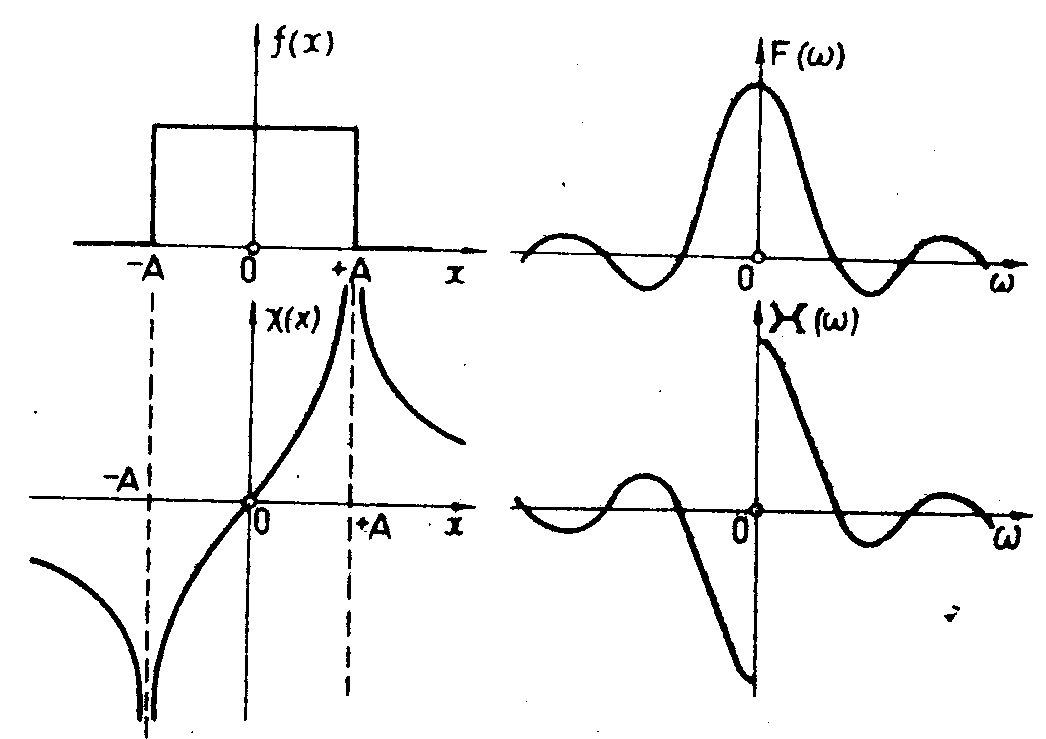
Рис.2. Пример преобразования Гильберта. Исходный сигнал -
- центрированный прямоугольный импульс. Гильберт-
-образ описывается логарифмической функцией.
Тот жe результат модно получить с помощью частотного фильтра g0(ω) (5).
3. Исходный сигнал имеет вид:
f3(x) =δ(x-x0)+δ(x+x0). (14)
Прямые вычисления дают (рис.3)
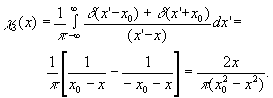 (15) (15)
Преобразование Гильберта позволяет компактно описать процессы, происходящие в системах связи с однополооыой модуляцией сигнала /1/. Действительно, в общем случае низкочастотный сигнал, регистрируемый на приемном конце, имеет вид
f н.ч.(x)=f(x)cosφ0-χ(x)sinφ0, (16)
где φ 0 - сдвиг фаз между несущей на передающем конце и колебаниями, создаваемыми местным генератором, на приемном конце. Из (16)
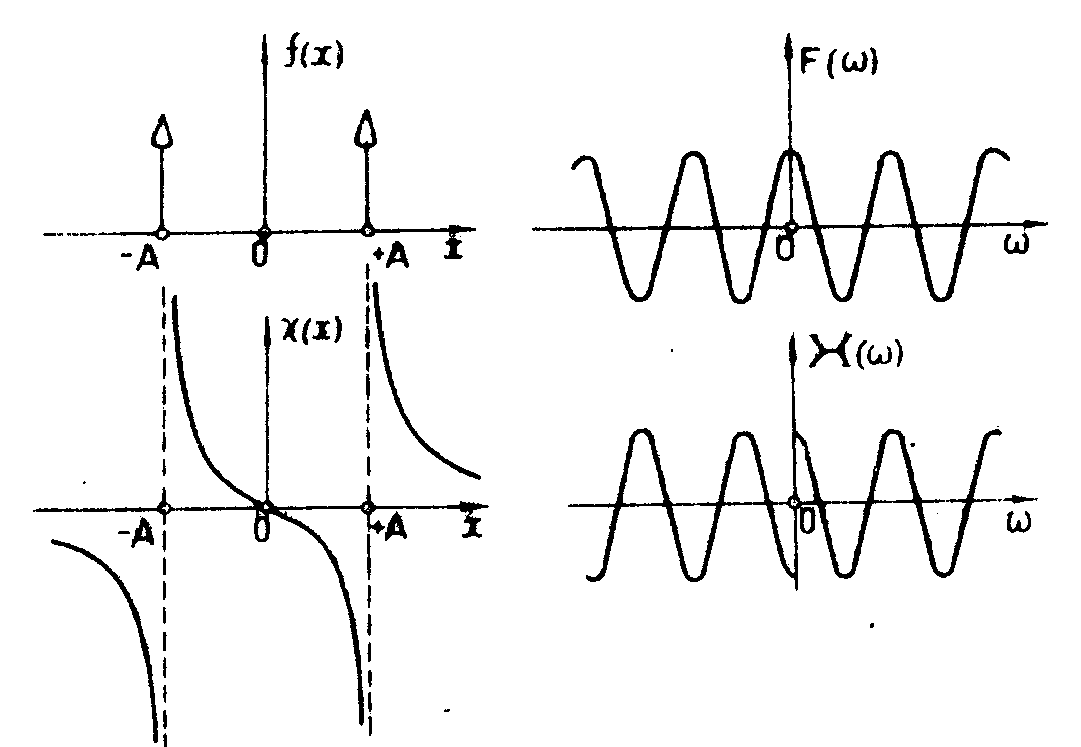
Рис.3. Пример преобразования Гильберта. Исходный сигнал -две дельта-функции, расположенные симметрично относительно начала координат.
видно, что принятый сигнал равен линейной комбинации переданного
сигнала f(х) и его гильберт-образа χ(х) . Если сдвиг фазы φ 0 равен нулю, то на приемном конце восстанавливается переданный сигнал f(х). Если φ0= 90°, т.е. местный генератор работает со сдвигом фазы на 90° по отношению к несущим колебаниям, то принятый сигнал равен гильберт-образу переданного сигнала.
2
Если входной сигнал f(x) удовлетворяет требования причинности, так что f(x) = 0 при x<0, то действительная и мнимая части его фурье-образа,
f(ω)=ref(ω)+iimf(ω), (17)
связаны соотношением Гильберта, а именно,
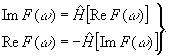 (18) (18)
Эти соотношения имеют прямое отношение к информационным свойствам голограммы Лейта. В простейшем случае плоской волны k (kСоsθ1-ksinθ1o ) интерференционная картина, образуемая опорной волной k0(k,o,о), имеет распределение интенсивности (рис.4):
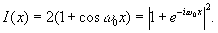 (19) (19)
Здесь 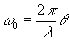 ,
λ - длина волны света. На стадии
восстановления образуется как плоская
волна k, так
и волна-двойник k'(kcosθ, ksinθ,o)
(рис.5). Появление волны-двойника k' исходной волны k вызвано тем, что фотоэмульсия
- это квадратичный детектор, откликающийся только на величину плотности энергии
в световой волне, и, как всякое нелинейное преобразование, операция возведения
в квадрат амплитуды поля создает новые частотные составляющие. Иначе говоря,
картина распределения интенсивности в плоскости голограммы одинакова как для
k+k0, так и для
k'+ k0 полей. ,
λ - длина волны света. На стадии
восстановления образуется как плоская
волна k, так
и волна-двойник k'(kcosθ, ksinθ,o)
(рис.5). Появление волны-двойника k' исходной волны k вызвано тем, что фотоэмульсия
- это квадратичный детектор, откликающийся только на величину плотности энергии
в световой волне, и, как всякое нелинейное преобразование, операция возведения
в квадрат амплитуды поля создает новые частотные составляющие. Иначе говоря,
картина распределения интенсивности в плоскости голограммы одинакова как для
k+k0, так и для
k'+ k0 полей.
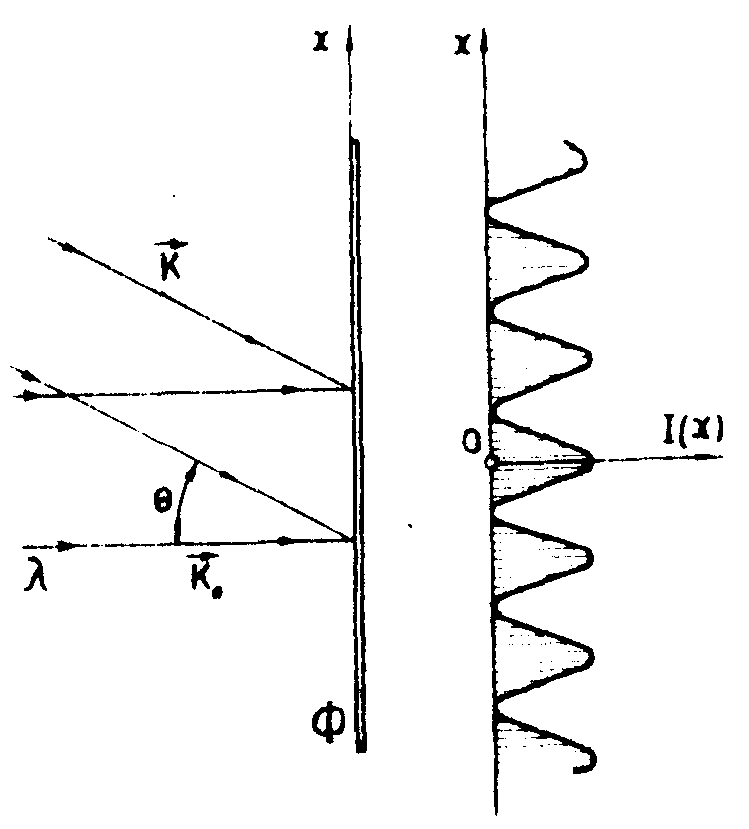
Рис.4. Схема получения голограммы Лейта. Используется плоская опорная волна.
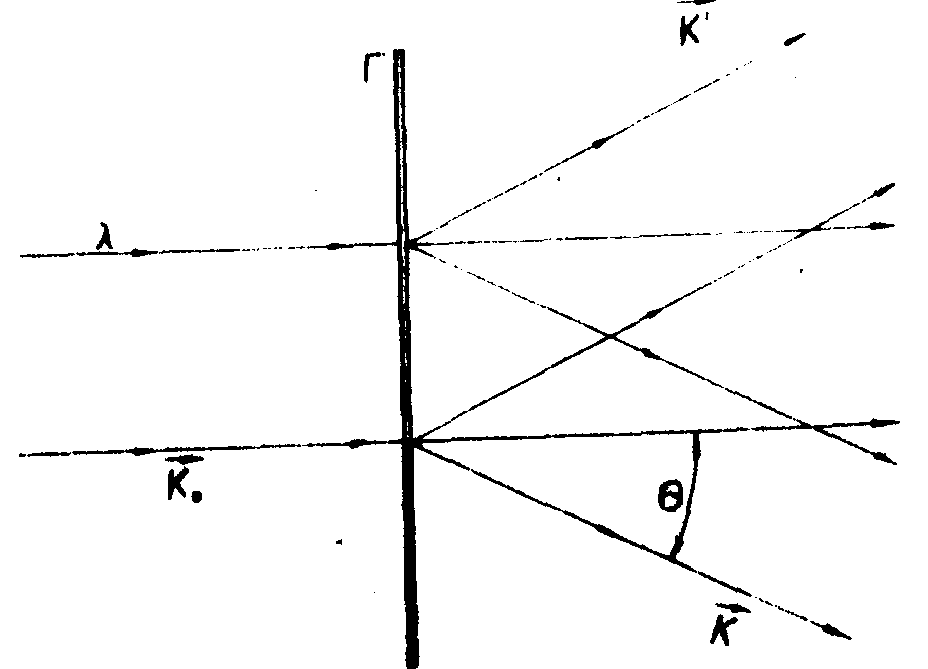
Рис.5. Стадия наблюдения восстановленной волны с помощью голограммы Лейта. Видна как плоская волна k, так и волна-двойник k'.
С помощью плоской голограммы невозможно установить, с какой стороны от опорного пучка k0 падала плоская волна на стадии регистрации голограммы, под углом +θ или под углом -θ. Наблюдатель должен знать заранее, что регистрируемое поле падает на фотоэмульсию только по одну сторону от опорного пучка k0. Иначе говоря, волна f(x) должна удовлетворять требованию причинности так, чтобы f(x)=0 при x<0. А это приводит нас к важному информационному выводу: на голограмме фактически регистрируются не две независимые функции, например, амплитуда и фаза, или действительная и мнимая части комплекснозначной функции, описывающей поле в плоскости голограммы, а всего только одна, так как вторая функционально однозначно связана с первой функцией соотношением Гильберта (18), и поэтому не несет никакой дополнительной информации.
Как известно, разрешающая способность фотоэмульсии для получения голограммы должна быть по крайней мере в четыре раза выше, чем в случае фотографии при заданном требовании на разрешение деталей в волновых полях, подлежащих регистрации.
Для того, чтобы доказать это, рассмотрим информационные свойства голограммы Лейта двух плоских волн k 1 и k2 (рис.6). Распределение интенсивности света голограммы в плоскости равно:
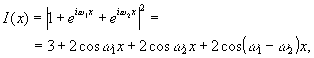 (20) (20)
где 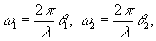 θ1
и θ2
- направление ориентации двух плоских волн. θ1
и θ2
- направление ориентации двух плоских волн.
На стадии восстановления (рис.7) образуется три группы волн:
две восстановленные волны в направлении +θ 12, и -θ1, две волны в направлении +θ2 и -θ2, а также волны на разностных пространственных частотах +(ω1-ω2) и -(ω1-ω2) Таким образом,каадая плоская волна создает своего двойника, а кроме того, образуются две чужеродные волны. Причина появления последних - нелинейные преобразования амплитуды поля в фотоэмульсия на стадии регистрации.
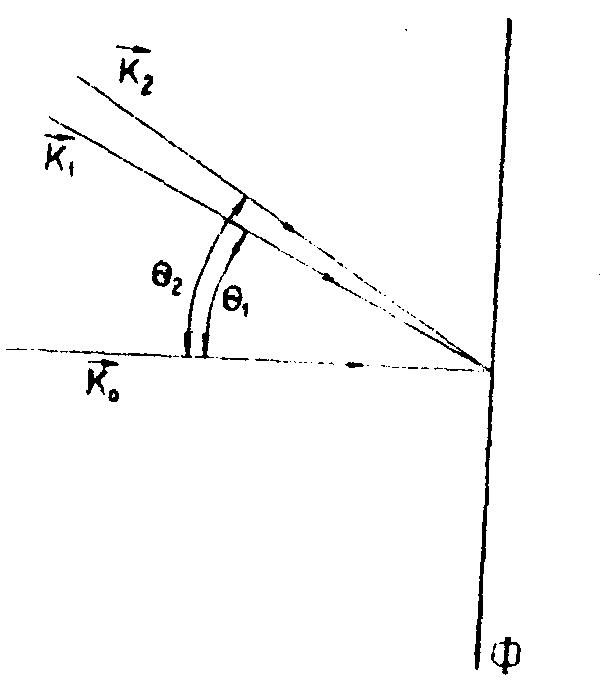
Рис.6. Схема получения голограммы Лейта двух плоских волн.
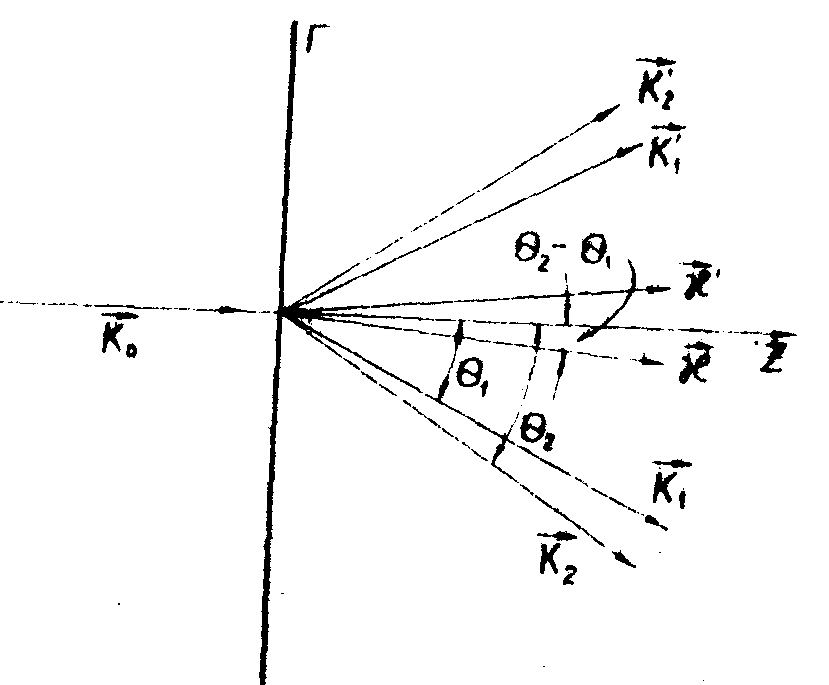
Рис.7. Стадия получения двух восстановленных волн с помощью голограммы Лейта. Появляются не только волны-двойники, но также чужеродные волны на разностных пространственных частотах.
Для того, чтобы эти чужеродные волны не попадали в раствор лучей между векторами k1 и k2 , достаточно, чтобы
ω 2-ω1≤ω1 (ω2> ω1)
или (21)
ω 2≤2ω1.
Если ввести среднюю частоту
ω 0 = 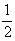 (ω1+ω2 (ω1+ω2)
(22)
и полосу пространственных частот
Ω = 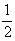 (ω2-ω1 (ω2-ω1)
(23)
то условия (21) принимают вид
ω 2 ≥ 4Ω. (24)
Именно это соотношение определяет требование к разрешающей способности фотоэмульсии для голограммы. Такова цена, которую приходится платить за то, что на голограмме регистрируются раздельно две функции пространственных координат.
Причина, по которой плоская голограмма не содержит метки о том, с какой стороны
от вектора опорной волны k0
идет плоская волна k,
заключается в том, что распределение интенсивностей в плоскости голограммы (19)
описывается только косинусом cosω0x .
А это не позволяет установить, в каком направлении возрастает фаза единичных
векторов 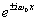 .
Направление вращения, между тем,
определяется синусом sinω0 .
Направление вращения, между тем,
определяется синусом sinω0x.
Голограмма, распределение интенсивности света в которое описывается синусом sinω0x , называется квадратурной голограммой. Для того, чтобы получить квадратурную голограмму /2/, делают независимую экспозицию, во время которой в опорный пучок вводят сдвиг фазы на π/2 (рис.8). Распределение интенсивности овета во второй, квадратурной, голограмме равно:
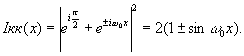 (25) (25)
Видно, что распределение интенсивности света относительно точки
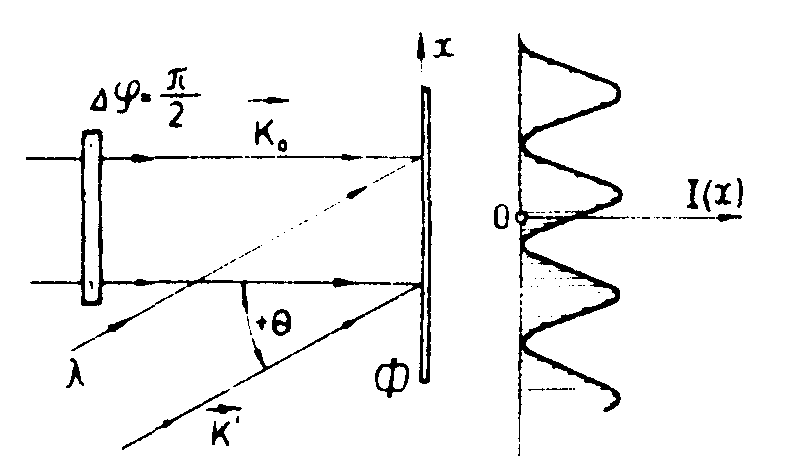
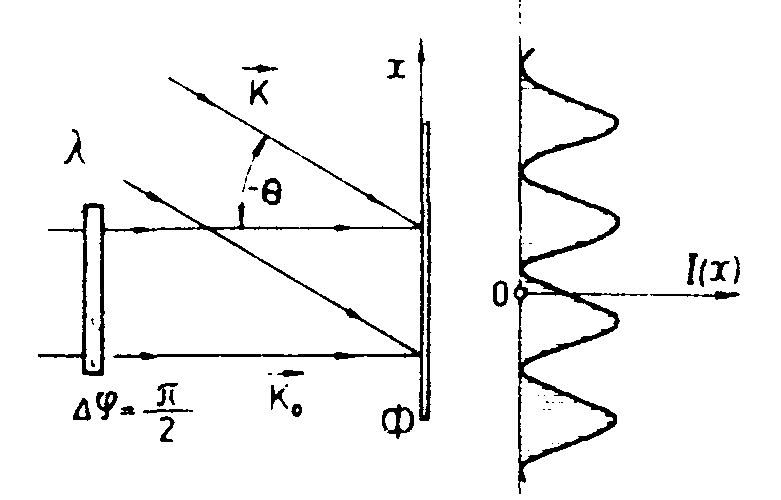
Рис.8. Схема получения квадратурной голограммы Лейта. В
опорную волну помещена фазовая пластинка, создающая сдвиг фазы на 90°. Видно, что сдвиг интерференционной картины на квадратурной голограмме относительно интерференционных полос на обычной голограмме зависит от того, с какой стороны от опорного пучка идет плоская волна, подлежащая регистрации.
х=0 зависит от того, с какой стороны идет плоская волна, под углом -θ (знак минус) или под углом +θ (знак плюс).
На стадии восстановления используют обе голограммы - обычную и квадратурную. При этом плоскость квадратурной голограммы располагается на расстоянии λ/4 от плоскости обычной голограммы. Волновое поле, синтезируемое с помощью системы светоделительных и светосинтезирующцх элементов, равно
u(x)=(1+cosω 0x)+i(1±sinω0x)=(1+i)+ 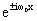 .
(26)
Поле волны-двойника здесь полностью отсутствует. Этот метод позволяет регистрировать голографические сцены, не удовлетворяющие требованию причинности. Снятие этого ограничения достигается использованием двух голограмм вместо одной. Здесь возникает еще информационный множитель 2. Таким образом, для того, чтобы зарегистрировать произвольную сцену на плоской голограмме, требуется записать в 8 (!) раз больше информации, чем в случае обычной фотографии. Напомним, что первый множитель 2 появляется из-за того, что регистрируют две функции, а не одну, как в фотографии. Второй множитель 2 вызван нелинейным по амплитуде преобразованием, происходящим в фотоэмульсии и в любом фотодетекторе. Наконец, третий множитель 2, появляющийся из-за наличия двух голограмм, обычной и квадратурной, связан со снятием ограничения на расположение сцены по одну сторону от опорного пучка.
Резюмируя, можно сказать, что процесс перехода от фотографии к подлинной голографии с использованием плоских регистрирующих сред шел через следущае этапы:
1) классическая фотопластинка отображает через распределения почернения соотношение интенсивностей света в двух произвольных точках плоскости; (рис.9) ничего не известно о соотношении полярностей электрических полей в двух точках, тем более ничего не известно о том, с какой стороны от нормали к фотопластинке шла световая волна;
2) в плоской голограмме благодаря введению опорного пучка рабочая точка сместилась в центральную часть характеристической кривой фотоэмульсии; (рис.10) при взаимной когерентности опорного и предметного пучков регистрируется информация о полярностях и значениях электрических полей в произвольных двух точках; однако, плоская голограмма не чувствительна к тому, с какой стороны от опорной волны идет предметная волна; чтобы такого вопроса не возникало, сцену располагают всегда по одну сторону от опорной волны;
3) при помощи системы, состоящей из двух плоских голограмм, взаимно квадратурных друг к другу в разнесенных на стадии восстановления по глубине на четвертую часть длины волны света, удается зарегистрировать информацию не только о величине и полярности электрических полей в оветовой волне, но также и о том, с какой
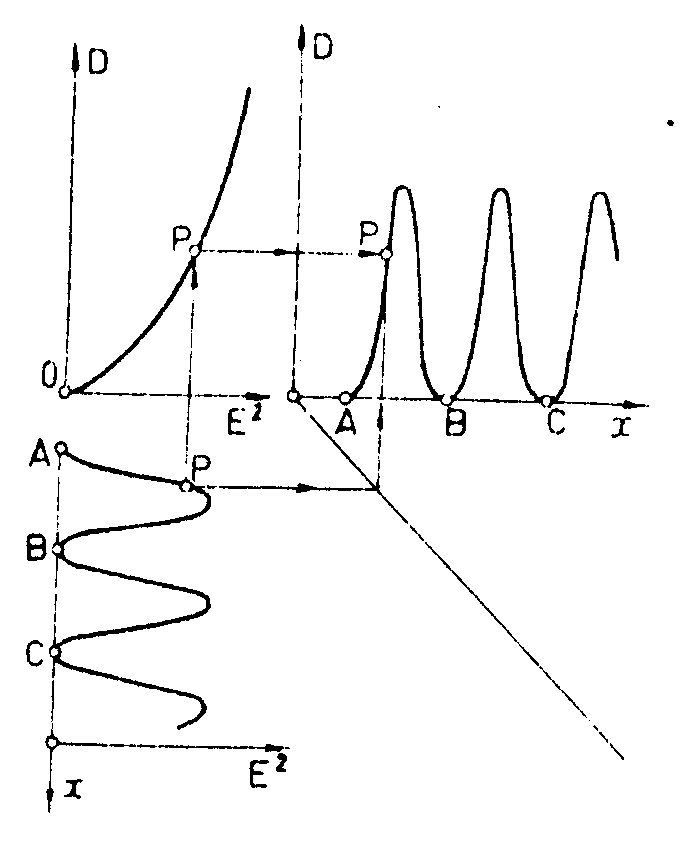
Рис.9. Информационная характеристика классической фотопластинки, которая не чувствует ни полярности электрических полей, ни направления, по которому идет плоская волна.
стороны от опорного пучка шла регистрируемая плоская волна.
В наших терминах это означает, что совокупность информации как о прямой, так и о квадратурной картинах интерференции двух волновых полей позволяет однозначно решить проблему полной регистрации волновых полей. При этом мы оставляем в стороне любые эффекты, связанные с поляризацией света.
3
Преобразование Гильберта можно использовать для визуализации малых сдвигов фаз. Как известно /1/, существует несколько методов исследования фазовых объектов. Это - метод фазового контраста Цернике /3/ (рис.11), интерференционный метод Тваймана /4/ (рис.12),
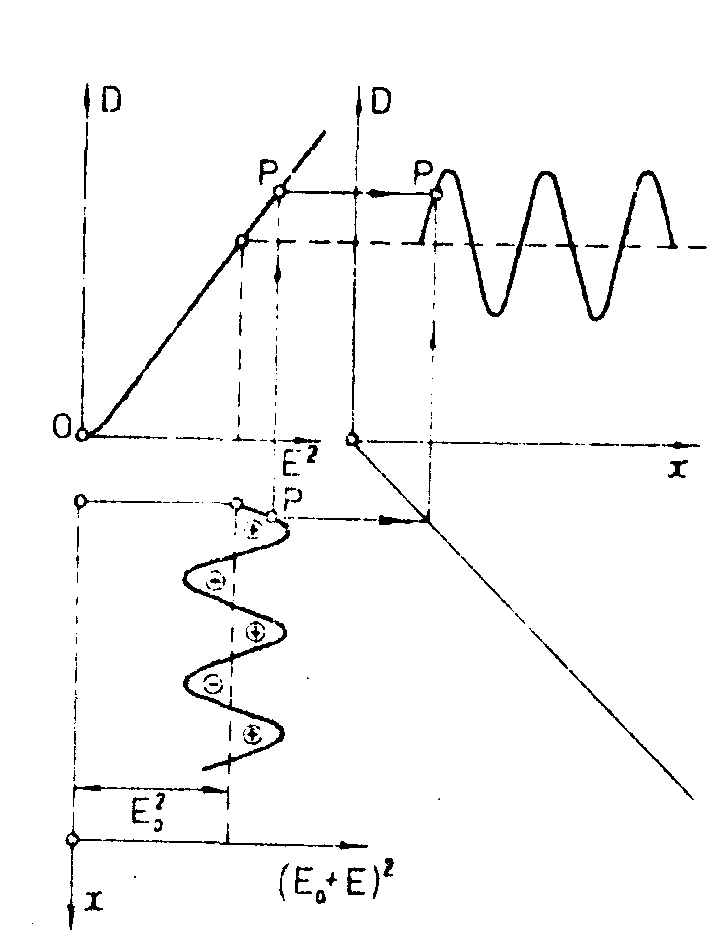
Рис.10. Информационная характеристика плоской голограммы. Рабочая точка сместилась в центральную область характеристической кривой фотоэмульсий. Регистрируются данные о величине поля и его полярности относительно опорной волны. Направления волн регистрируются неоднозначно.
интерференция в поляризованном свете. Методы интерференции, особенно в поляризованном свете, дают высокую чувствительность в обнаружении слабых фазовых сдвигов. Однако, это преимущество остается только в области средних и высоких пространственных частот, а при очень низких пространственных частотах их применение оказывается ограниченным /5/. Это связано о тем, что в методе фазового контраста в частотную плоскость системы двойной дифракции вводят поглощающий или дифазирующий диск. Поэтому всегда существует, "мертвая зона", задерживающая информацию о низких пространственных частотах. Если же размеры диска сделать малыми, то возникают помехи
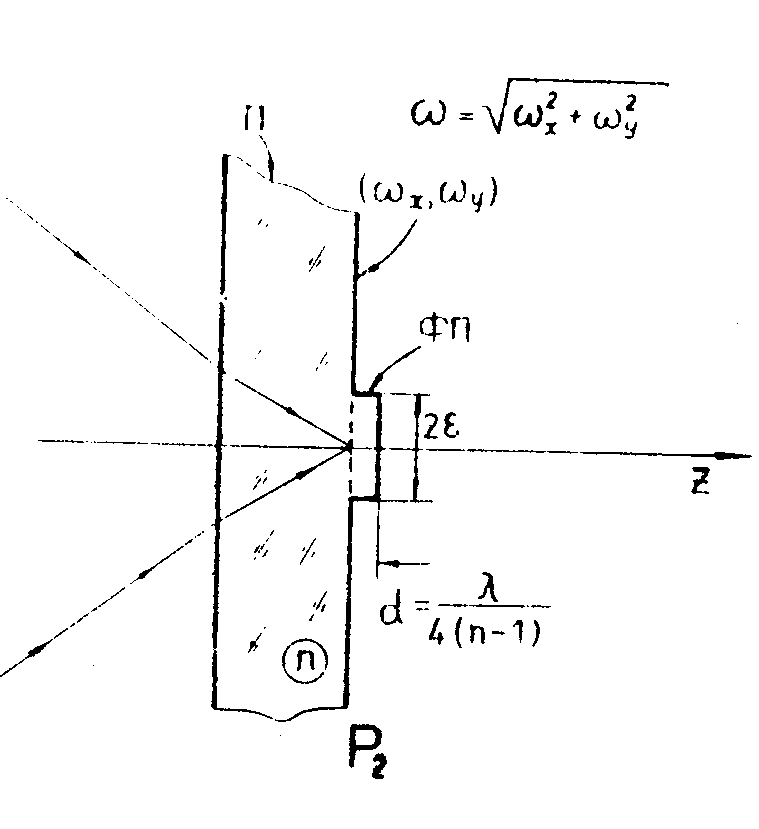
Рис.11. Метод фазового контраста Цернике. Линзы λ 1 и λ2 осуществляют два следующих друг за другом преобразования Фурье - прямое и обратное. В центре плоскости пространственных частот установлена фазовая пластинка ФП, создающая фазовый сдвиг Δφ=π/2. Β плоскости изображения и фазовый контраст отображается в виде контраста интенсивности.

Рис.12. Интерференционный метод Тваймана визуализации фазовых
неоднородностей. Трассы интерферирующих пучков полностью разделены. s - источник монохроматического света, d -светоделитель, λ1 и λ2 - коллимируищие линзы, М1 - плоское зеркало, М2 - выпуклое сферическое зеркало, λ0 - испытуемый фотографический объектив. Испытуемая деталь пронизывается светом дважды. Систеvа позволяет определять знак фазовых попаданий, который определяется направлением смещения полос при увеличении расстояния между зеркалом М, и светоделителем d.
в виде дифракционной картины от края диска, устранить которые можно, если использовать метод ножа Фуко /6/ (рис.13).
Метод ножа Фуко дает хорошую визуализацию изучаемого волнового фронта, однако в случав малых фазовых сдвигов также возникает помеха от дифракции, и чтобы учесть ее, с неизбежностью приходится рассматривать гильберт-образ объекта. Сначала оптики использовали
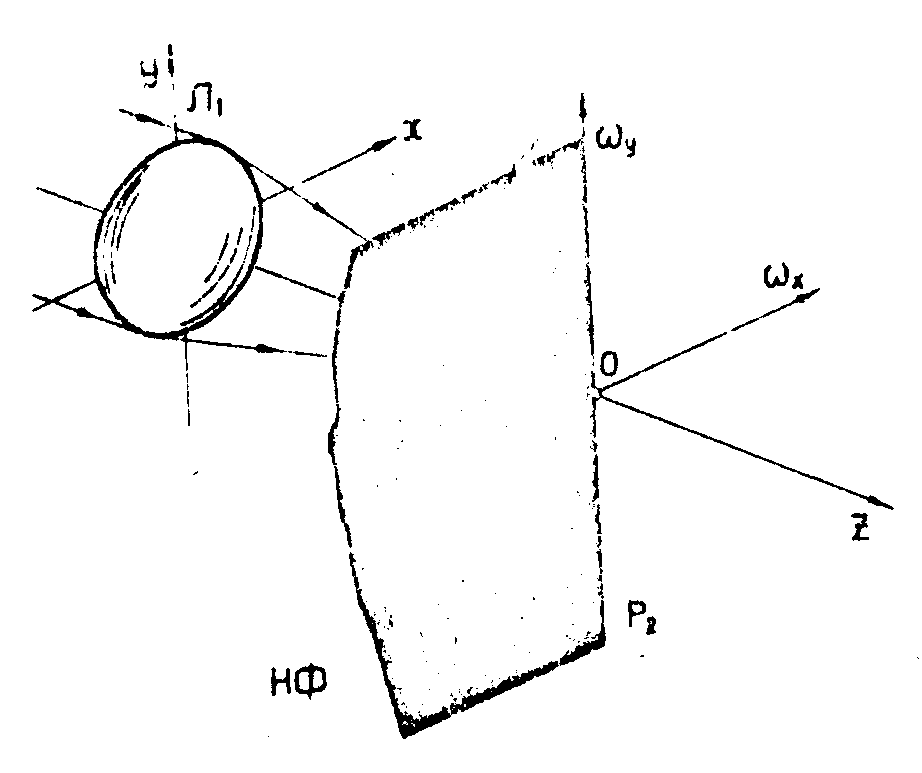
Рис.13. Визуализация фазового объекта П с помощью ножа Фуко, помещаемого в плоскость пространственных частот. Нож Фуко-НФ срезает половину спектра пространственных частот объекта.
в частотной плоскости фазовый нож, (рис.14) чтобы осуществить в системе двойной дифракции пространственное преобразование Гильберта /7/. Наиболее удачные результаты были получены в зеркальной системе /5/ (рис.15). Затем преобразование Гильберта удалось осуществить при помощи источника белого света /8/. Наконец, в работах /9,10/ была предложена дифракционная решетка со сбоем, которая позволяет разделить в пространстве сам объект и его гильберт-образ. Эта система проста и дает устойчивые результаты.
Преобразование Гильберта в традиционной оптической системе двойной дифракции осуществляется путем помещения фазового ножа в пространственно-частотную плоскость. Здесь возникают проблемы:
центрировка на оси фазового ножа, точность сдвига по фазе и другие.
Преобразование Гильберта является частным случаем линейной фильтрации /1/. Поскольку пропускание со интенсивности фильтра Гильберта g0(x) равно единице, то отфильтрованное изображение содержат всю энергию сигнала, без потери. Действительно, в силу
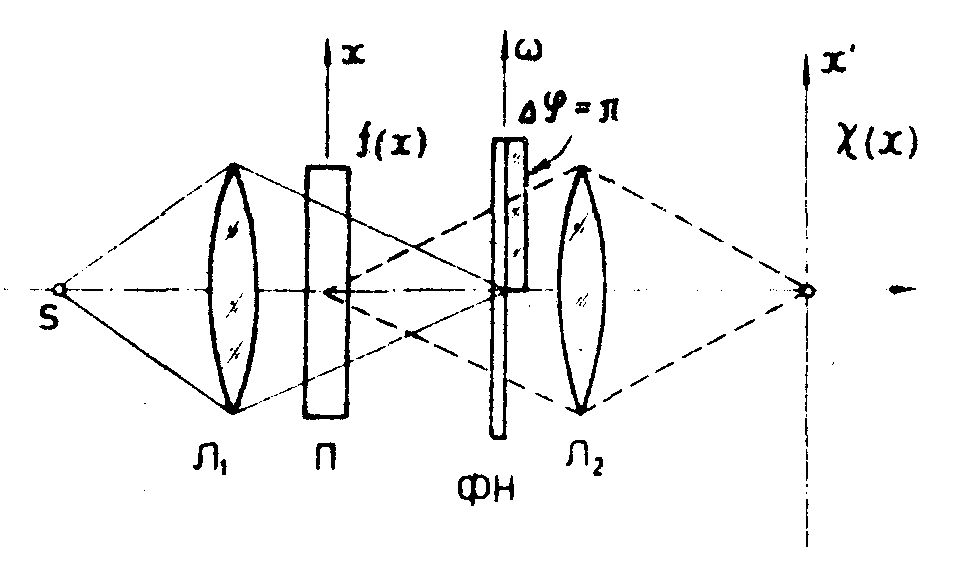
Рис.14. Визуализация фазового объекта П с помощью фазового ножа, осуществляющего преобразование Гильберта фазового объекта. Фазовый нож НФ создает одвиг фазы Δ φ=π β половине спектра пространственных частот объекта. Линзы λ1 и λ2 выполняют преобразование Фурье, прямое и обратное.
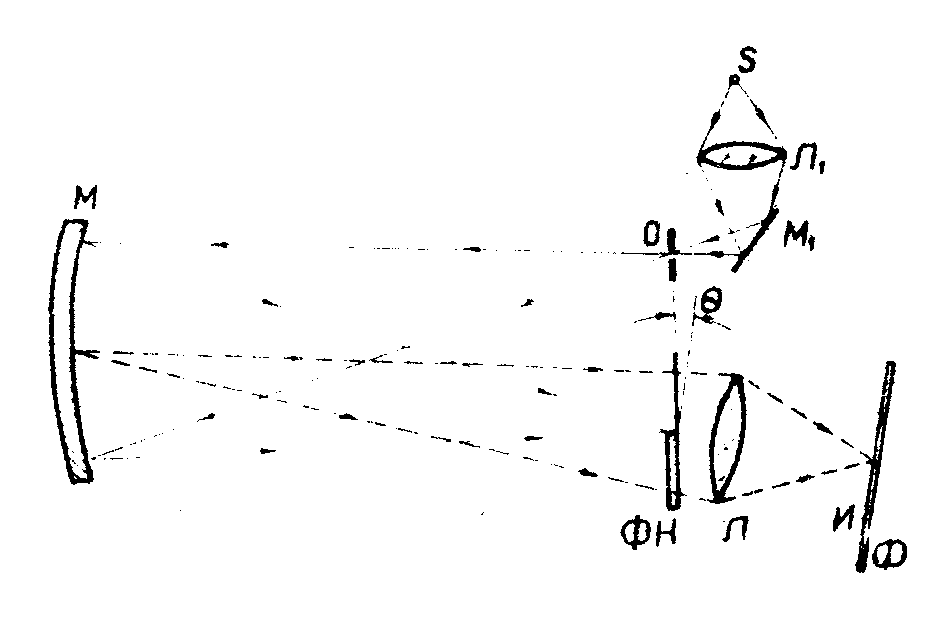
Рис.15. Зеркальная система, осуществляющая преобразование Гильберта без помех, вызванных паразитными полями, которые возникают при прохождений света через объективы, состоящие из нескольких склеенных линз.
теоремы Парсеваля
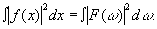 (27) (27)
Последнее выражение для
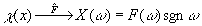 (28) (28)
переходит в
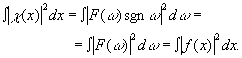 (29) (29)
В отличив от метода ножа Фуко или метода фазового контраста, где часть энергии света поглощается а экранах, в системе о преобразованием Гильберта в отфильтрованное изображение идет вся энергия входного сигнала.
Рассмотрим метод визуализации Фазового контраста с помощью фазового ножа Гильберта /5/.
Пусть объект f(x) имеет слабую вариацию фазы в апертуре диаметром d:
 (30) (30)
где α <<1, , а пространственная частота Ω также мала. В пренебрежении высшими порадками имеем
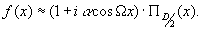 (31) (31)
Первое слагаемое в (31) после преобразования Гильберта,согласно (12) и (13), переходит в
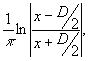
а второе слагаемое в (31),согласно (11) дает
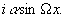
При малых х
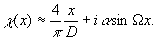 (32) (32)
Из (32) видно, что существуют такие х 0= 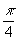 d α,
χто при х<х0
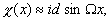 (33) (33)
а интенсивность света в плоскости изображения равна
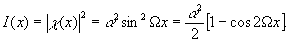 (34) (34)
Легко видеть, что гильберт-образ четной функции всегда является нечетным, и наоборот, гильберт-образ нечетной функции является четной функцией. Отсюда следует, что если фазовый рельеф объекта симметричен, то его гильберт-образ имеет одну темную линию, указывающую положение максимума фазового рельефа. При этом точность локализации оси симметрии в случае фазового ножа Гильберта оказывается более высокой, чем в случае метода ножа Фуко.
Это вызвано тем, что сигнал, отображаемый в системе визуализации фазового рельефа о помощью ножа Фуко, представляет собой наложение гильберт-образа сигнала о самим исходным сигналом. Действительно, нож Фуко, устанавливаемый в плоскости пространственных частот, срезает половину пространственных частот входного сигнала. Такая операция эквивалентна умножению фурье-образа f(ω) на функцию Хевисайда y(ω), γде
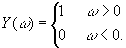 (35) (35)
На выходе ножа Фуко сигнал описывается функцией /1/
Φ(ω)= f(ω)y(ω). (36)
Используя теорему свертки, находим
φ(υ )=f(x)⊗u(x) (37)
где u(x) - Фурье-образ функции Хевисайда:
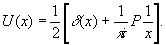 (38) (38)
Окончательно получаем отфильтрованное изображение
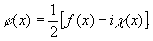 (39) (39)
Тот же результат получается, если учесть, что функция пространственного фильтра Фуко имеет вид
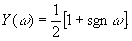 (40) (40)
Распределение интенсивности в отфильтрованном изображении системы Фуко,
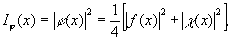 (41) (41)
не содержит интерференционных членов в силу ортогональности компонент в (39).
Если объект имеет вид
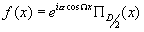 (30) (30)
или при α <<1
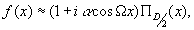 (31) (31)
то при малых х, согласно (32),
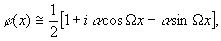 (42) (42)
а распределение интенсивности
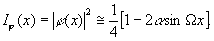 (43) (43)
Если же исходный сигнал имеет вид центрированного прямоугольного импульса:
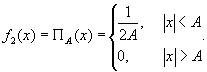 (12) (12)
то нож Фуко превратит его в функцию
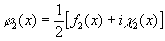 (44) (44)
с распределением интенсивности
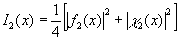 (45) (45)
4
Произведем сопоставление различных методов визуализации фазовых объектов.
Первый метод наблюдения малых фазовых искажений сводится к наблюдению интерференции двух волновых полей с помощью интерферометра /4/. Распределение интенсивности имеет вид
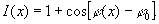 (46) (46)
В качестве универсального параметра сравнения различных методов берем контраст интенсивности;
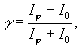 (47) (47)
где i0 - освещенность фона, iφ - освещенность в области фазового дефекта.
Если φ 0=0 , а φ(х) мало, то i(х) =1 и γ=0.
Если φ =π/2, то контраст интенсивности γ= φ (x), т.е. очень мал.
Существуют также дифференциальные интерферометры с использованием явления поляризации. Однако, для объектов с низкими пространственными частотами контраст получается также малым, так как фазовые дефекты визуализируюгся в этом методе по величине своей пространственной производной, которая в случае низких пространственных частот весьма мала.
Поэтому для объектов с низкими пространственными частотами применим только метод ножа Фуко и метод фазового ножа с использованием преобразования Гильберта, и как будет показано ниже, метод фазового ножа оказывается более чувствительным, чем метод ножа Фуко.
Как следует из (34), контраст картины распределения света в плоскости Гильберта от фазового синусоидального объекта в области x<<x0, равен ≈i. В случае изображения Фуко, согласно (43), контраст равен 2α, что существенно меньше i при α<<1. Таким образом, метод ножа с использованием преобразования Гильберта дает более высокий контраст, чем в методе Фуко. Причина преимуществ метода фазового ножа состоит в том, что здесь нет интенсивной равномерной засветки, которую создает нож Фуко (45).
Равномерную засветку можно убрать с помощью поглощающего фильтра пространственных частот. Однако из-за конечного размера поглощающего фильтра будут задержаны также и низкие пространственные частоты. Кроме этого, процесс дифракции на непрозрачном экране создает засветку по всему полю, что ослабляет контраст отфильтрованного изображения. В случае фазового ножа, имеющего большие размеры, паразитные эффекты дифракции в центре поля практически отсутствуют. Высокий контраст здесь удается достичь благодаря удивительному свойству преобразования Гильберта: постоянную засветку оно концентрирует на краях поля в форме светящихся серпиков (рис.16). Однако, выигрыш в чувствительности в методе фазового ножа с использованием преобразования Гильберта достигается ценой уменьшения полезного поля, поскольку контраст,согласно (32), уменьшается до значения γ=1/2
Рис.16. Гильберт-образ плоской и однородной монохроматической волны света, полученной с помощью фазового ножа.
при х ≅х0. Однако, в оптических системах всегда присутствует рассеянный свет, который ослабляет чувствительность. Если γ0 -наименьшее значение контраста, воспринимаемого наблюдателем, а i0 - уровень паразитной засветки, то наименьший сдвиг фаз, который может быть обнаружен в методе фазового ножа с использованием преобразования Гильберта, равен /5/
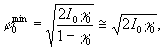 (48) (48)
в то время, как в метода ножа Фуко этот сдвиг фаз равен
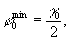 i0=1. (49) i0=1. (49)
Если γ 0≈1/50 и i0≈10-4, то
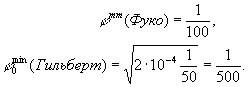 (50) (50)
Таким образом, в данных условиях метод фазового ножа обладает чувствительностью в 5 раз выше, чем метод ножа Фуко.
5
Обычно фазовый ноа изготавливается путем нанесения на стекло диэлектрического слоя, толщина которого выбирается такой, чтобы разность фаз между двумя полями равнялась π для рабочей длины волны λ, а поглощение света было бы пренебрежимо малым. Как правило, граница раздела полей в фазовом ноже не попадает точно на средний линию картины дифракции далекого поля, отображаемую в плоскости пространстаенных частот.
Рассмотрим общий случай фильтра пространственных частот, который составлен из двух пластинок, расположенных вплотную друг к другу с различной оптической толщиной и с различным поглощением /5/. Обозначим через τ eiθ - комплексное пропускание по амплитуде одной пластинки относительно другой. Фильтр пространственных частот, составленный, из двух пластинок, имеет амплитудное пропускание
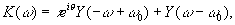 (51) (51)
где ω 0 - координата линии раздела в плоскости пространственных частот. Как модно показать, преобразование фурье перевощит функции Хэвисайда в их образы:
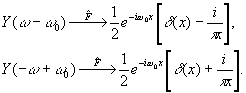 (52) (52)
Передаточная функция такого фильтра, т.е. отклик на точечное изображение δ(х), имеет вид
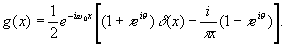 (53) (53)
Исходный сигнал f(х) преобразуется о помощью такого фильтра в отклик системы, равный
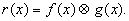 (54) (54)
Выражение (53) охватывает все возможные случаи:
1) τ =1, θ=0 - свободная апертура в частотной плоскоcти;
2) τ≤ 1, θ=±π/2 - фазовый контраст;
3) τ=1, θ=π - фазовый ном Гильберта;
4) τ=0 - нож Фуко.
При помощи соотношения (53) исследуем влияние на качество изображения в систеке с фазовым нoжoм Гильберта следующих факторов:
а) эффекта поглощения диэлектрического слоя;
б) эффекта дефазировки;
в) децентрировки фазового ножа в плоскости пространственных частот и конечной ширины источника света;
г) децентрировка источника.
А. Эффект поглощения
Пусть θ=π, ΰ τ=1-ε. Импульсный отклик системы равен
 (55) (55)
Выходной сигнал
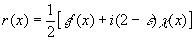 (56) (56)
переходит в гильберт-образ λ(х) при ε=0, т.е. когда нет различия в поглощении обоих пластинок. Если функция f(x) имеет определенную четность, т.е. f(x) - четная или нечетная, то картина распределения интенсивности
i(x)=| χ(x)|2
обладает симметрией относительно лпнии х=0. В общем виде распределение интенсивности
i(x)=|r(x)|2=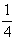 { { ε2|f(x)| 2+(2- ε)2|χ(x)|2+2im[ε(2-ε)f(x)χ*(x)]}
(57)
на испытывает влияния поглощения одной из пластинок на свойство симметрия, далее если его поглощение сделать полным, как в случае ножа Фуко (ε =1).
Б. Эффект дефазировки
Если разность фаз θ отлична от π, так что θ =π-α, ςо импульсный отклик системы равен
g(x)=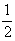 [(1-e [(1-e -iα)δ(x)- 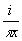 (1+e-iα)]≈ (1+e-iα)]≈
≈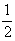 [iαδ(x)-
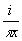 (2-iα)].
(58) (2-iα)].
(58)
Выходной сигнал равен
r(x)= 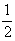
[iαf(x)+i(2-iα)χ(x)], (59)
а распределение интенсивности в плоскости изображения равняется
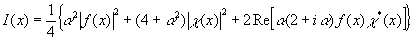 (60) (60)
Видно, что дефазировка разрушает свойство симметрии изображения.
В. Децентрировка фазового ножа
Импульсный отклик системы в атом случае равен
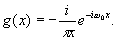 (61) (61)
Для объекта
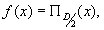
где диаметр поля зрения
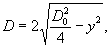
в случае кругового поля получаем отклик системы
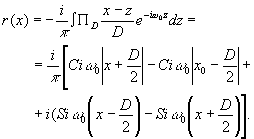 (62) (62)
Г. Децентрировка источника
Это приводит к наклону волны под углом α и отклик системы становится равным
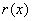 ~ ~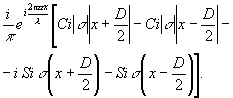 (63)
(63)
Здесь С i и si - интегральные косинус и синус. Например,
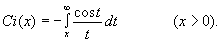 (64) (64)
6
Методы когерентной фурье-оптики находят широкое применение в системах обработки двухмерной информации и распознавания образов. Для получения Фурьe-образа двухмерного сигнала, заданного в виде транспаранта, собирающую линзу устанавливают непосредственно за
транспарантом, а наблюдения ведут в фокальной плоскости Р 2 (рис.17). Чтобы изготовить голографический согласованный фильтр, фотоэмульсию, которая располагается в фокальной плоскости, освещают когерентным опорным пучком.
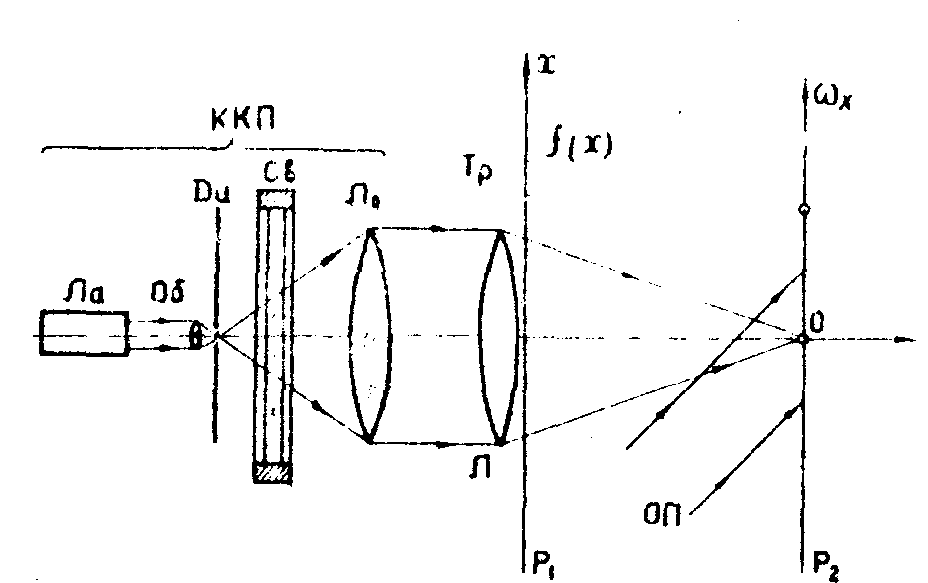
Рис.17. Практическая схема оптического каскада, осуществляющего двухмерное преобразование Фурье. ККП - когерентный коллимированный пучок света, λ1 - собирающая линза, Тр - транспарант с входным сигналом f(х) Р2 - фокальная плоскость, Ф - экран. Для получения согласованного голографического фильтра эмульсия, помещаемая в плоскости экрана, освещается опорным пучком ОП.
Если входные сигналы достаточно просты, например, состоят из отрезков прямых линий, то визуальное наблкдение в фокальной плоскости Р 2 позволяет получить сведения об основных характеристиках входных сигналов. Однако, если сигналы А и Б не обладают необходимыми свойствами симметрии, то их различить нельзя, так как их макроскопические картины дифракции далекого поля оказываются тождественными (рис.18).
Кроме известных методов устранения указанной неоднозначности, существует также простой метод визуального наблюдения, заключающийся в совместном анализе, как картины дифракции далекого поля, так
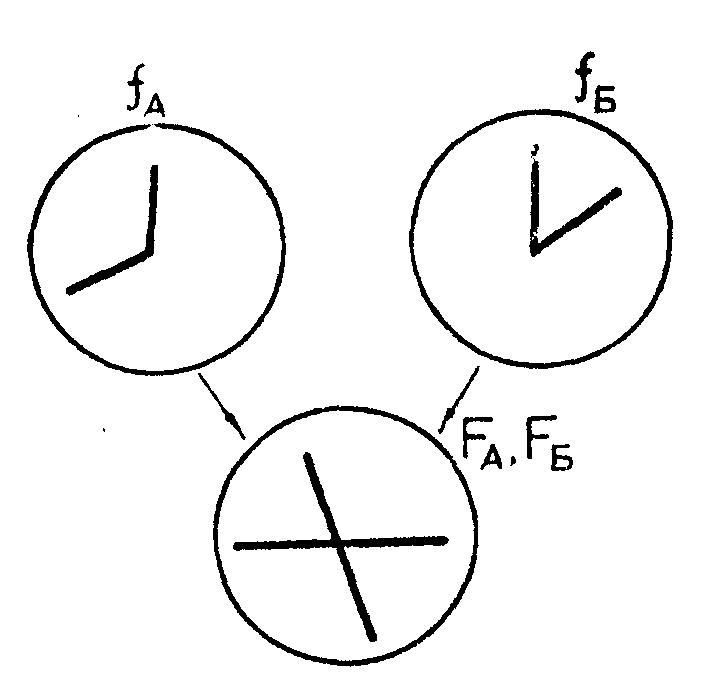
Рис.18. Сигналы А и Б, дающио тождественные макроскопические картины дифракции далекого поля.
и его гильберт-образа. Такая процедура стала бы практически удобной, если бы удалось одновременно получить как дифракцию далекого поля от транспаранта с исходным сигналом, так и гильберт-образ дифракции далекого поля.
Как будет показано ниже, это удается осуществить с помощью новой дифракционной
решетки /9-12/,
которая отличается от классической тем, что две смежные бороздки в ее центре
разнесены на расстояние, равное 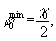 ,
где α - шаг дифракционной решетки, n
- целое число, обычно выбираемое равным n=1
или n=2 (рис.19). ,
где α - шаг дифракционной решетки, n
- целое число, обычно выбираемое равным n=1
или n=2 (рис.19).
Принцип работы дифракционной решетки со "сбоем" проиллюстрируем на примере теневого прибора, который преобразует фазовый контраст в контраст интенсивности (рис.20). Дифракционную решетку со сбоем поыещавт в плоскость пространственных частот. Вторая линза λ 2 осуществляет обратное преобразование Фурье. Если оптическая ось системы проходит через центр плоскости между двумя аномальными бороздками решетки, то это значит, что дифракционная решетка со сбоем, выполняющая функцию фазово-контрастного фильтра, центриро-
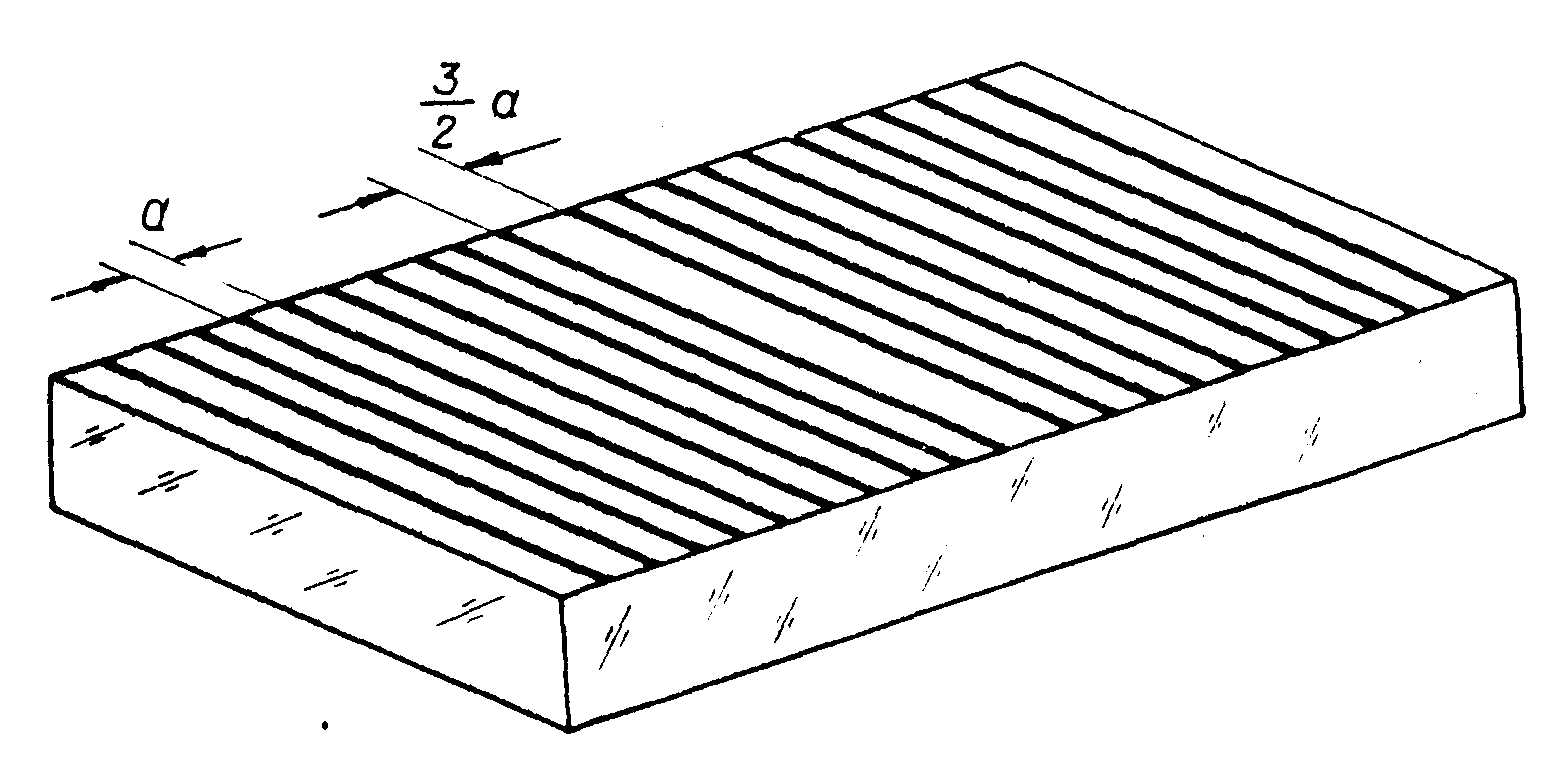
Рис.19. Общий вид дифракционной решетки со сбоем. Сбой в центре решетки на ±α/2, где α - шаг решетки задает новые функциональные свойства такой решетки.
вана относительно оптической оси. Источник света также расположен на оптической оси. В этом случае амплитудное пропускание дифракционной решетки со сбоем описывается функцией g(ω) , γде
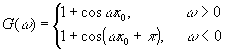 (65) (65)
или
g(ω)=1+cosωx 0 sgnω. (66)
После обратного преобразования Фурье, осуществляемого линзой λ 2, в плоскости Р3 отобразиться сигнал
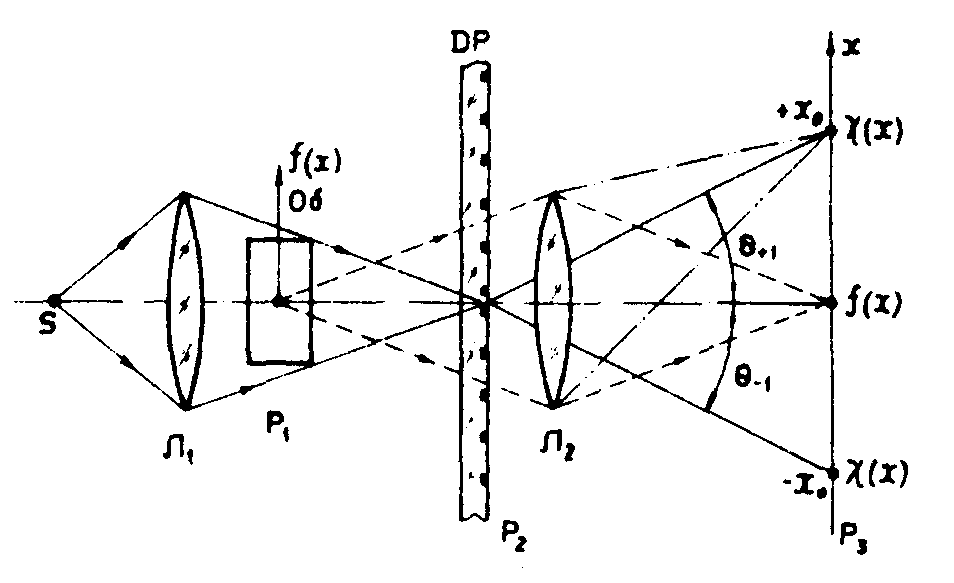
Рис.20. Схема теневого прибора визуализации фазового
контраста с использованием дифракционной решетки со сбоем. s - источник света, λ1 - линза прямого преобразования Фурье, Р1 - входная плоскость, в которой находится исследуемый образец О, Р2 - плоскость пространственных частот, ДРС - дифракционная решетка со сбоем, λ2 -линза обратного преобразования Фурье, Р3 - входная плоскость, в которой установлен экран для наблюдения преобразованного изображения объекта. В нулевом порядке дисаракции отображается сам объект, в первых порядках дифракции - его гильберт-образ.
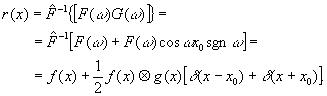 (67) (67)
Здесь
 (68) (68)
Учитывая определение преобразования Гильберта (1), запишем (68) в следующем виде:
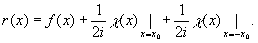 (69) (69)
Первое слагаемое в (69) описывает нулевой порядок, который отображает исходный сигнал f(x) без каких-либо изменений. Второе слагаемое, отображаемое в первом порядке дифракции, равно гильберт-образу входного сигнала, причем, он сосредоточен относительно точки х=х0, которая является центром поля первого порядка дифракции. Третье слагаемое, также равное гильберт-образу, располагается вокруг точки х=-х0, в минуо первом порядке дифракции.
Сдвиг центра поля первого порядка дифракции от оптической оси равен
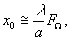 (70) (70)
где λ - длина волны света, fΩ - фокусное расстояние линзы λ2. Из (70) видно, что с изменением длины волны света происходит сдвиг первого порядка дифракции. В отличие от ранее рассмотренных оптических методов осуществления преобразования Гильберта, дифракционная решетка со сбоем не требует никаких котировок по фазе. Более того, если излучение состоит из двух длин волн, достаточно разнесенных друг относительно друга, то можно наблюдать гильберт-образы одновременно при двух разных длинах волн. Традиционными методами этого достигнуть невозможно, если только не использовать светоделительные устройства и не вести наблюдения в лучах только одной длины волн.
Существенным достоинством дифракционной решетки со сбоем является ее нечувствительность к вариациям температуры и влажности. В дифракционной решетке со сбоем практически отсутствуют пограничные эффекты, которые имеют место при использовании фазового ножа.
Наконец, полностью отпадает забота о выборе угла между оптической осью и плоскостью фильтра в виде дифракционной решетки со сбоем. Как известно, эта операция является самой трудной в гильберт-системах и занимает много времени.
Дифракционные решетки удобно совмещать вместе. Благодаря отсутствию каких-либо юстировок, кроме совмещения центра решетки о оптической осью, оптическая система, выполняющая одновременно несколько преобразований Гильберта, достаточно проста.
Например, если две дифракционные решетки со сбоем совместить так, чтобы их бороздки были взаимно перпендикулярные установить в плоскости пространственных частот, то такой фильтр отобразит сразу три разных гильберт-образа /9/ (рис.21).
1) Одномерный гильберт-образ двухмерного сигнала f(x,у), причем, преобразование Гильберта ведется вдоль оси х:
 (71) (71)
2) Одномерный гильберт-образ двухмерного сигнала f(x,у) когда преобразование Гильберта ведется вдоль оси у:
 (72) (72)
3) Двухмерный гильберт-образ двухмерного сигнала f(х,у) когда преобразование Гильберта ведется одновременно вдоль оси х и вдоль оси у:
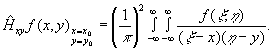 (73) (73)
Соответственно, первые два образа сосредоточены в двух первых порядках дифракции, а третий образ находится в перекрестном порядке
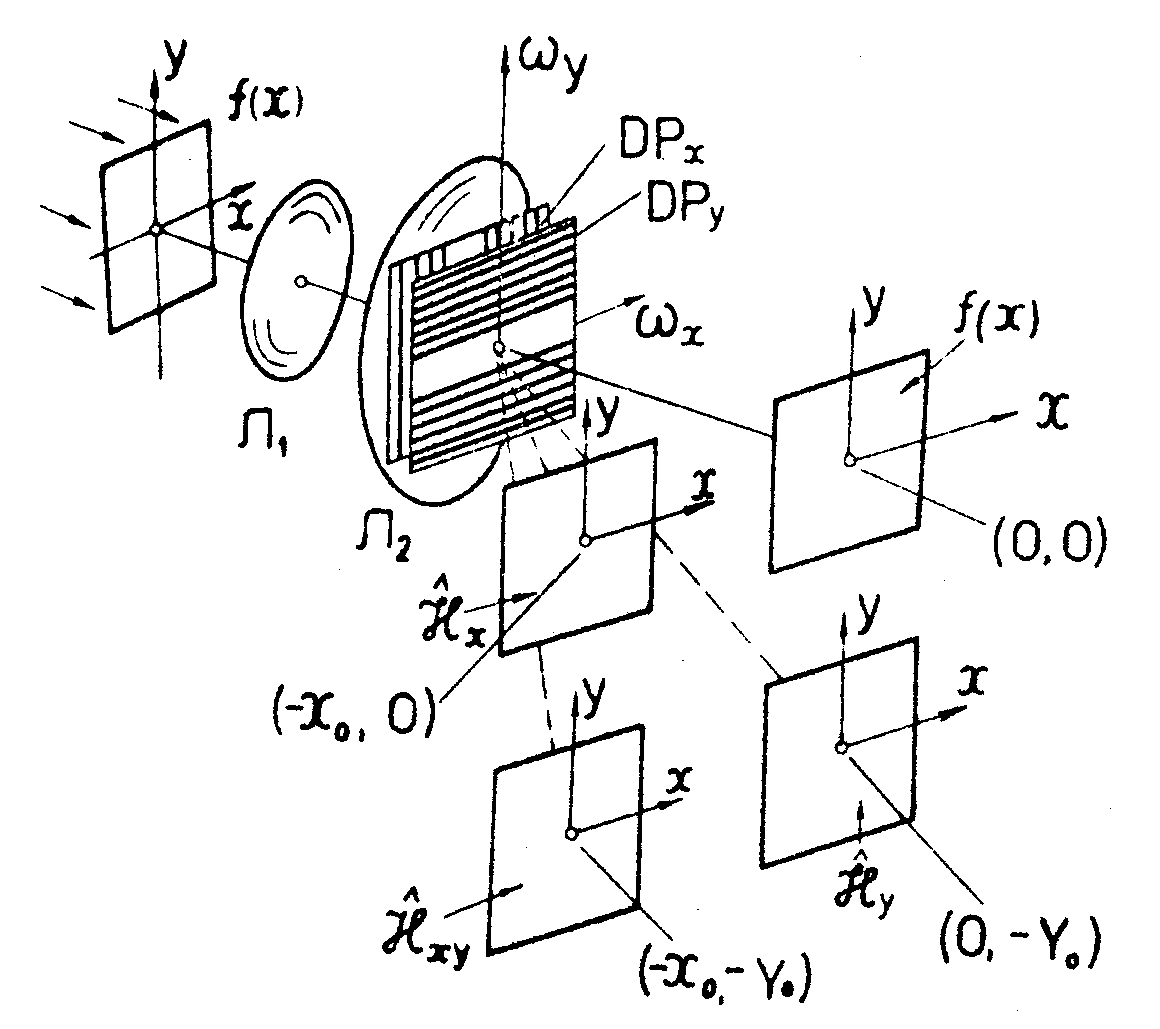
Рис.21. Совмещение двух дифракционных решеток со сбоем в оптичаском каскаде. Штрихи решеток перпендикулярны друг другу и центрированы на оптической оси. В выходной плоскости отображаются сразу три различных гильберт-образа входного сигнала f(х). Два одномерных гильберт-образа, по оси х и по оси у, сосредоточены в первых порядках дифракции от каждой дифракционной решетки со сбоем. Двухмерный гильберт-образ находится в перекрестном порядке совместной дифракции света на двух решетках.
дифракции.
7
Если шаг между смежными образами в центре дифракционной решетки со сбоем отличается от величины "а", определенной выше, то функция g(ω), характеризующая амплитудное пропускание решетки, имеет теперь вид (рис.22):
g α(ω)=cos(ωx 0-α)y(ω)-cos(ωx0+α)y(-ω). (74)
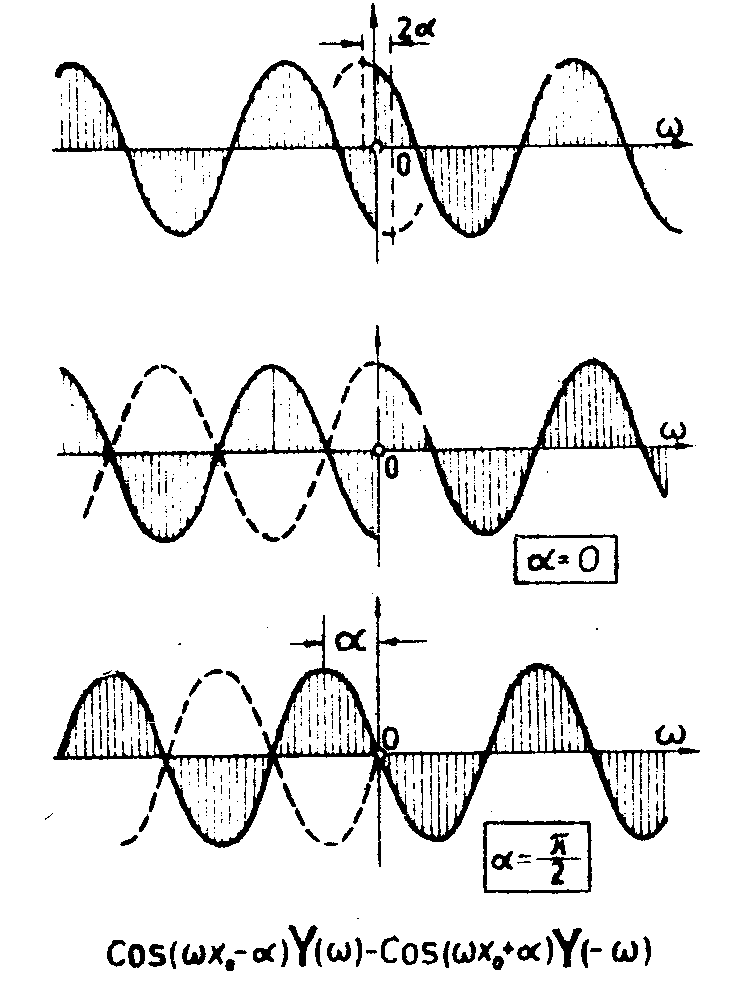
Рис.22. Структура дифракционной решетки с аномальным сбоем. Угол α характеризует степень отступления шага между двумя смежными образцами в центре дифракционной решетки со сбоем от расчетного значения.
Фаза α задает степень отступления значения шага между двумя смежными бороздками от расчетного значения "а", которому соответствует α=0. Соотношение (74) записано для дифракционной решетки со сбоем, центр которой расположен точно на оптической оси системы.
Найдем амплитуду поля, которое создает дифракционная решетка с аномальным сбоем в выходной плоскости. Запишем (74) следующим образом:
g α(ω)=cos(ωx0-α)y(ω)-cos(ωx0+α)y(-ω)=
=cosωx 0cosα|y(ω)-y(-ω)|+ (75)
=sinωx 0sinα|y(ω)+y(-ω)|.
Если учесть, что
y( ω)-y(-ω)=sgnω
, (76)
y( ω)+y(-ω)=1
то
g α(ω)=cosωx 0 cosα sgnω+
+sinωx 0sinα. (77)
В выходной плоскости появится сигнал:
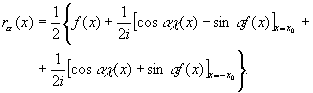 (78) (78)
Из (78) видно, что в нулевом порядке дифракции отображается исходный сигнал f(х), а в первых порядках дифракции расположены линейные комбинации исходного сигнала f(х) и его гильберт-образа
χ(x) . Примесь f(x) -компоненты полностью исчезает при α=0.
Наиболее близким аналогом эффекта наложения сигнала и его гильберт-образа в дифракционной решетке с аномальным сбоем является подобный эффект в системах связи на одной боковой полосе или ssb (см. стр. 4). Различие между дифракционной решеткой со сбоем и ssb -системой заключается в том, что дифракционная решетка со сбоем служит для того, чтобы отобразить гильберт-образ входного сигнала без каких-либо искажений, в то время как в системах связи на одной боковой полосе стремятся в чистоте восстановить сам исходный сигнал.
Линейная комбинация исходного сигнала и его гильберт-образ отображаются также в классической системе Фукo-Теплера с использованием ножа Фуко в плоскости пространственных частот (рис.13). Напомним, что для ножа Фуко амплитудное пропускание фильтра равно
k( ω)=y(ω)=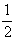 [1+sgnω].
(79) [1+sgnω].
(79)
Амплитуда поля в выходной плоскости определяется
r(x)= 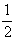 [f(x)-iχ(x)].
(80)
Соответствующее распределение интенсивности имеет вид
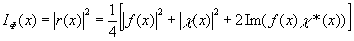 . (81) . (81)
Поскольку для действительных входных сигналов f(x) их гильберт-образ всегда является действительным, то третье слагаемое в (75) всегда равно нулв. Таким образом,
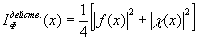 (82) (82)
не содержит интерференционных членов.
Амплитуда поля, создаваемого дифракционной решеткой с аномальным сбоем в поле первого порядка дифракции, описывается выражением /8/:
rdp (x)=cosα χ(x)-sinα f(x). (83)
Распределение интенсивности содержит прямой интерференционный член:
idp(x)=|cos α χ(x)-sinα f(x)|2=
=cos2 α |χ(x)|2+sin2α|f(x)|2- (84)
-2sin α cosα re[f(x) χ*(x)].
Для входных сигналов, которые описываются действительными и симметричными относительно точки х=0 функциями,имеем (рис.23 а,б,в,г,д)
idp(x)=cos2 α |χ(x)|2+sin2α|f(x)|2-
-sin2 α f(x) χ(x). (85)
Если α =π/4, то cos2(π/2) = sin2(π/4)=1/2, sin(π/2)=1 и
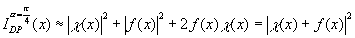 (86) (86)
Напомним, что в силу ортогональности функций f(x) и χ(х), т.е. в силу того, что
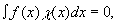 (87) (87)
суммарный вклад интерференционного члена в (86) равен нулю.
Рассмотрим теперь эффекты, возникающие из-за деюстировки дифракционной решетки со сбоем /10/. Функция g(х), задающая амплитудное пропускание дифракционной решетки со сбоем, которая установлена в плоскости пространственных частот с эксцентриситетом Δ ω κ оптической оси, имеет вид
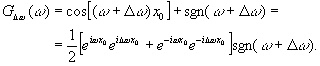 (88) (88)
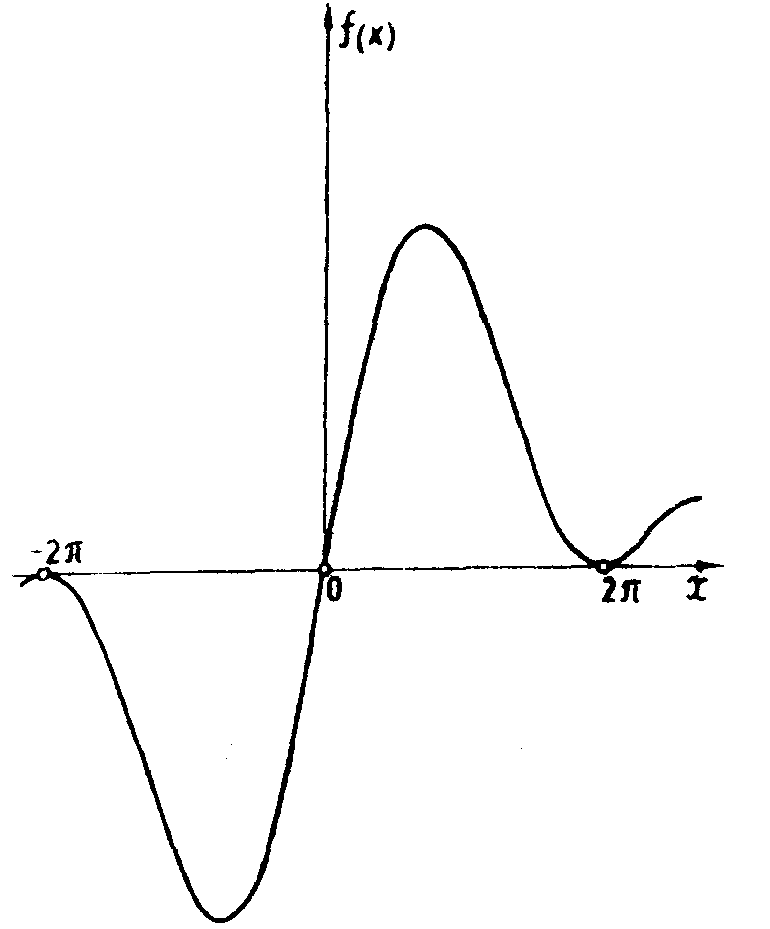
Рис.23а.
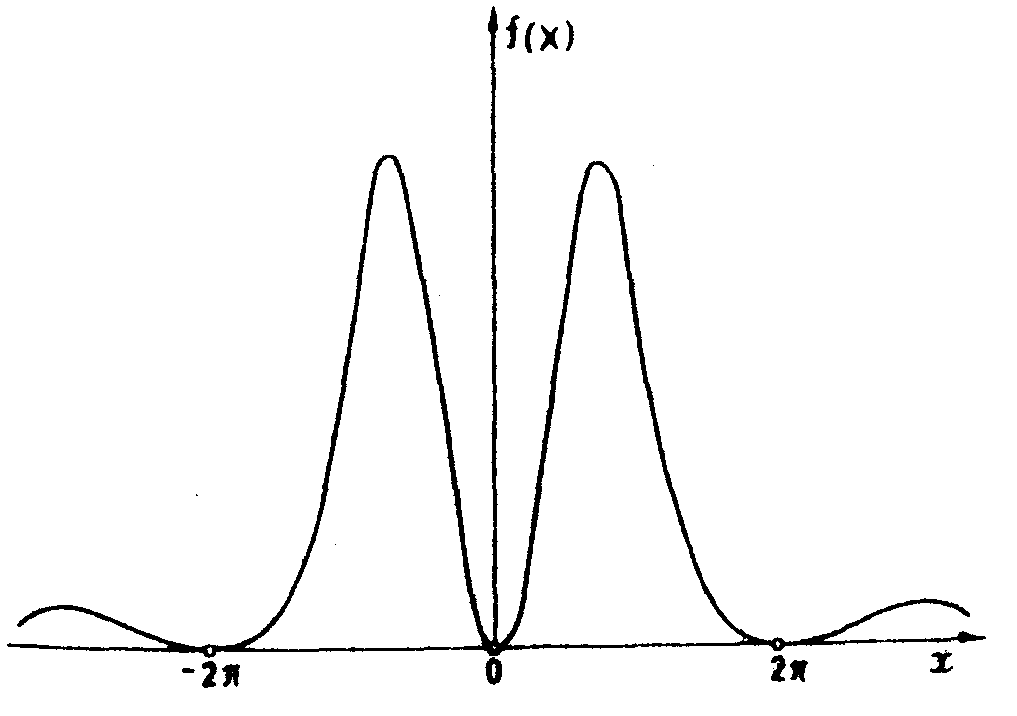
Рис.23б.
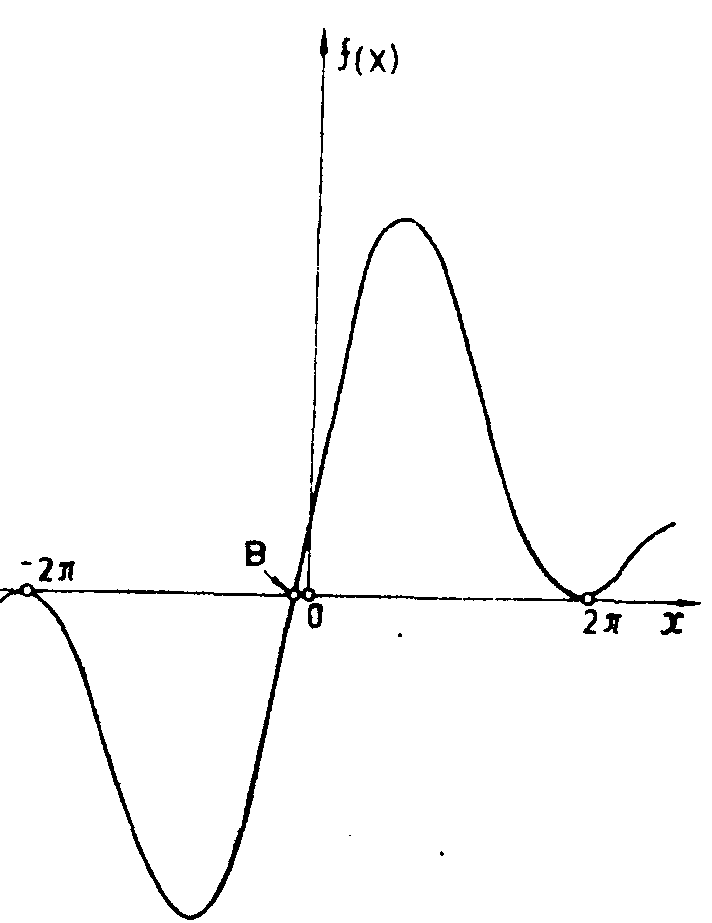
Рис.23в.
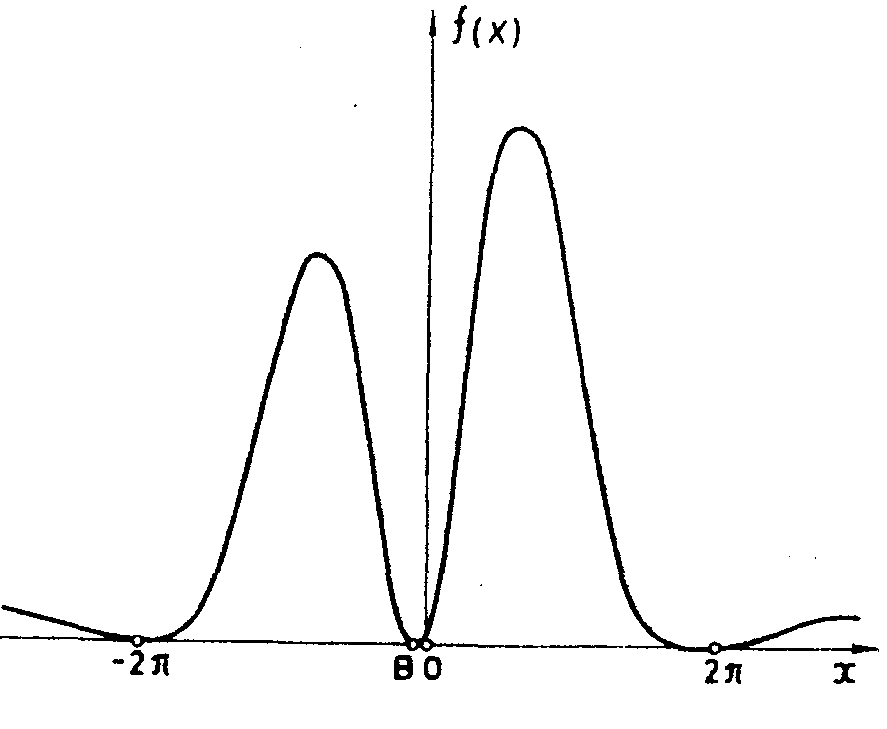
Рис.23г.
д)
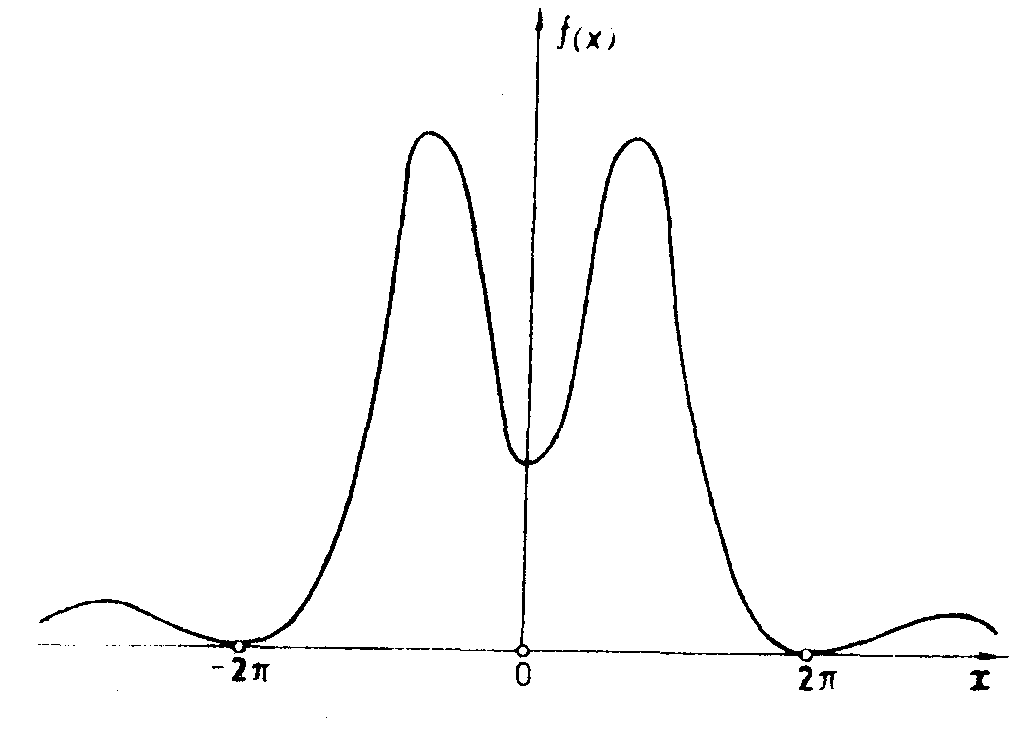
Рис.23. Эффект когерентного наложения Гильберт-образа и примеси исходного сигнала в дифракционной решетке с аномальным сбоем, когда α мало:
а) амплитуда поля гильберт-образа узкой щели;
б) распределение интенсивности в гильберт-образе узкой щели;
в) сумма амплитуды поля гильберт-образа узкой щели и небольшой примеси амплитуды узкой щели;
г) распределение интенсивности поля, полученного от наложения на гильберт-образа небольшой примеси самого входного сигнала;
д) распределение интенсивности поля от фазового ножа с диэлектрическим покрытием, полуплоскости в котором имеют небольшое различие в коэффициенте поглощения.
Если учесть, что
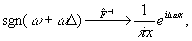 (89) (89)
то сигнал r(x) в выходной плоскости равен
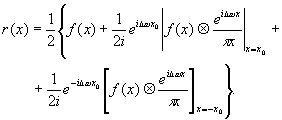 (90) (90)
Можно показать, что
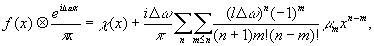 (91) (91)
где μ m - момент функции f(x) с номером m, равный по определению
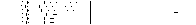 (92) (92)
Поскольку Δ ω μало, а контраст в отфильтрованном изображении наибольший в точке х=0, то в первом приближении амплитуда поля вблизи точки х=0 имеет вид
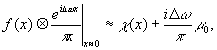 (93) (93)
а распределение интенсивности поля
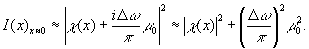 (94) (94)
Из (94) видно, что небольшая деюстировка дифракционной решетки со сбоем приводит к тому,что появляется паразитная равномерная засветка в центре поля(рис.24). Это приводит к ослаблению контраста. В то же время это свойство можно с успехом использовать для визуального контроля наличия деюстировки дифракционной решетки со сбоем и для ее устранения.
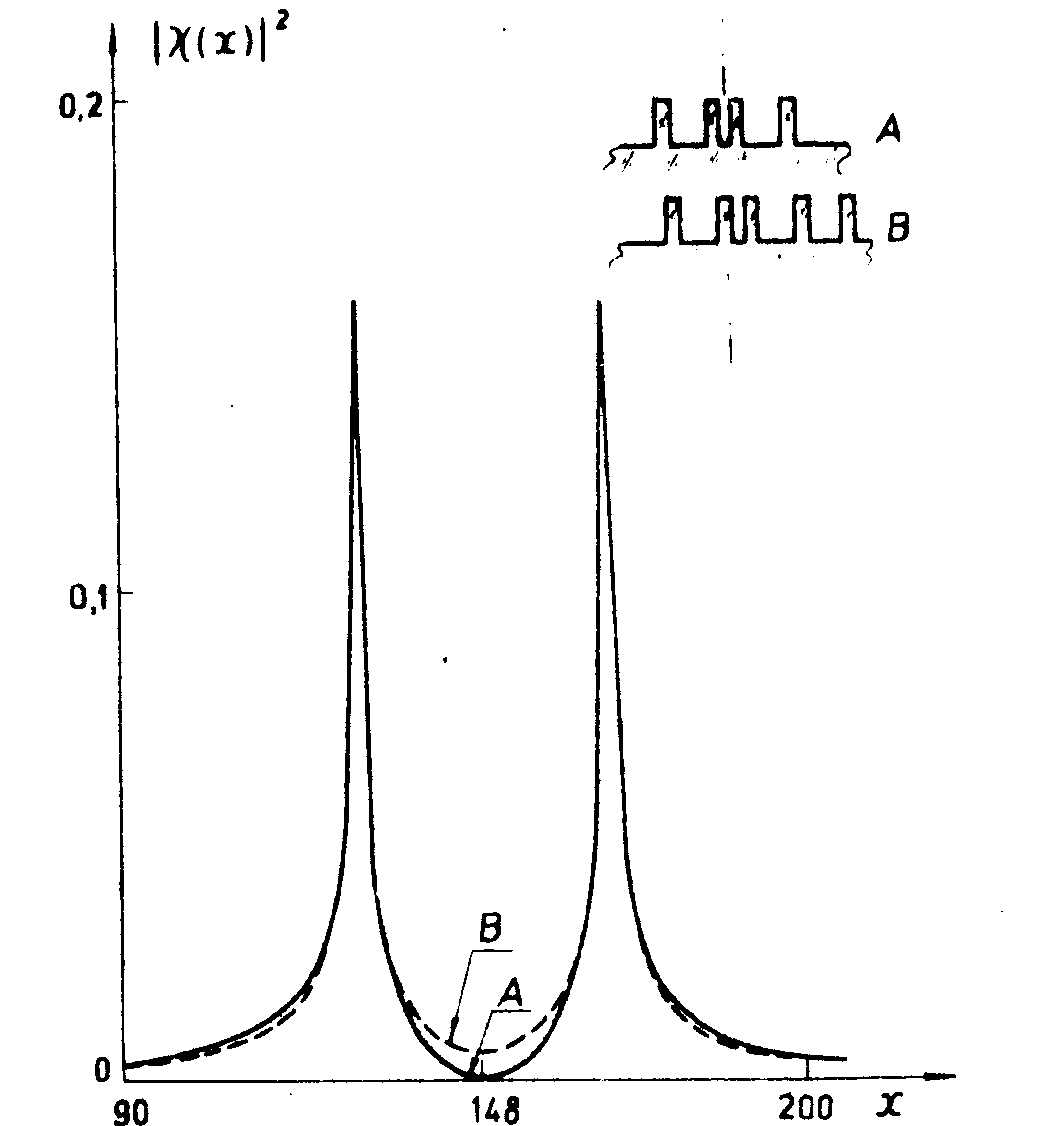
Рис.24. Эффект децентровки дифракционной решетки со сбоем. Сплошная кривая от правильно центрированной решетки. Пунктирная кривая - от децентрированной решетки со сбоем. В верхней части рисунка показано расположение двух смежных бороздок дифракционной решетки со сбоем по отношению к оптической оси.
8
Дифракционная решетка со сбоем может быть использована в анализаторе одномерных сигналов, предотввлвшшх в виде "силуэтного" изображения f(х,y), пропускание в котором равно i в области, ограниченной осью х и контуром сигнала, но равно нулю вне атой области /13/. Силуэт функции является биполярным. Положительные значения функция расположены сверху над осью х, а отрицательные - снизу под осью х. Отрицательные значения функции f(х,y) обеспечиваются тем, что на пути световой волны, освещающей нижнюю часть транспаранта, установлена фазосдвигающая пластинка, оптическая тол-
щина которой равна половине длины волны света. Её можно заменять дифракционной решеткой со сбоем (рио.25). Устанавливая считывающие устройства, соответственно, на плоскости пространственных частот в точках ω =ω0 и ω=0, можно одновременно измерять, как спектр анализируемого одновременного сигнала, так и некоторый суммарный эффект от искаженно-выпрямленного сигнала.

Рис.25. Дифракционная решетка со сбоем в анализаторе спектров одномерных сигналов, представленных в виде "силуэтного" изображения.
Как уже отмечалось выше, дифракционная решетка со сбоем позволяет отображать при помощи простых оптических средств, с малыми затратами времени на операции юстировки, одновременно несколько различных гильберт-образов. Проиллюстрируем эту возможность на примере алгоритма распознавания образов путем одновременного наблюдения шести интегральных образов: трех фурье-образов и трех гильберт-образов. Принцип работы такого алгоритма распознавания сводится к отказу от операций сканирования в алгоритме коррелятора, которые заменены в новом алгоритме нелинейным преобразованием картины распределения интенсивности в выходной плоскости.
Входной сигнал f(х,у) подвергался одновременно шести интег-
ральным преобразованиям (рис.26). С помощью цилиндрической оптики отображают два фурье-образа: одномерный Фурье-образ
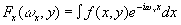 (95) (95)
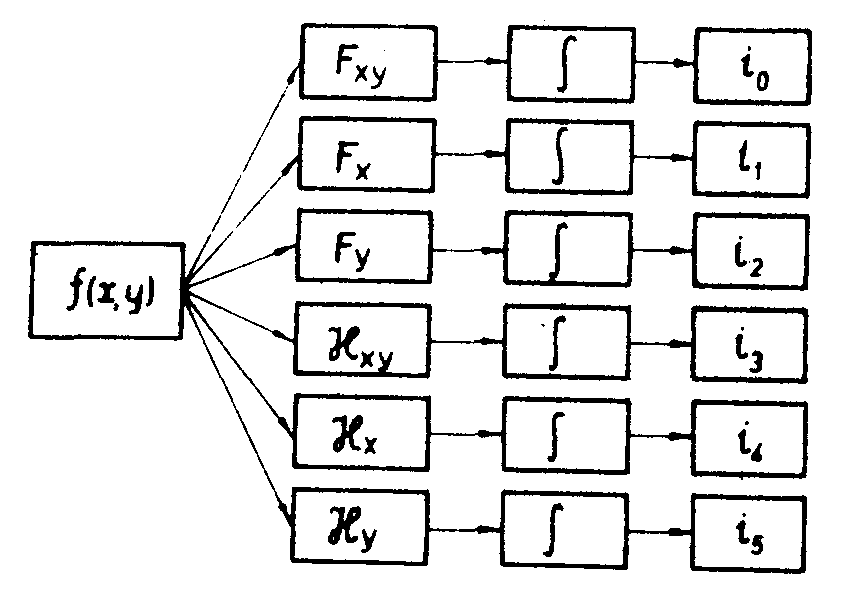
Рис.26. Алгоритм распознавания с использованием шести информационных признаков. Входной сигнал расщепляется на шесть каналов. В первых трех каналах производится два одномерных и одно двухмерное преобразование Фурье. В последних трех каналах производится два одномерных и одно двухмерное преобразование Гильберта. На выходе каждого канала имеются нелинейные преобразователи.
двухмерного сигнала, причем,преобразование Фурье ведется вдоль оси х, одномерный Фурье-образ
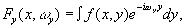 (96) (96)
когда преобразование Фурье ведется вдоль оси у. Кроме этого, с помощью сферической собирающей линзы отображают двухмерный фурье-
-образ
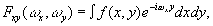 (97) (97)
когда преобразование Фурье ведется как вдоль оси х, так и вдоль оси у.
Если использовать две скрещенные ортогонально дифракционные решетки со сбоем, то, как было показано выше (71,73), в первых порядках дифракции каждой решетки отобразятся одновременные гильберт-
-образы, когда преобразование Гильберта ведется либо вдоль оси х, либо вдоль оси у, а в перекрестном порядке дифракции этих решеток отобразится двухмерный гильберт-образ, когда преобразование Гильберта ведется одновременно, как вдоль оси х, так и вдоль оси у.
В качестве информационных признаков алгоритма распознавания были взяты следующие шесть показателей, являющихся нелинейными образами картины распределения интенсивности:

Выбранные шесть информационных признаков чувствительны к ориентации входного сигнала. С помощью моделирующих расчетов на ЭВМ были вычислены эти показатели для некоторых простейших оигналов: двух трековых событий и нескольких букв латинского алфавита. В таблице, приведенной ниже, даны значения этих показателей (рис.27). Видно, что критерии отбора с использованием шести показателей оказываются существенно более мощными, чем для одного критерия i0.
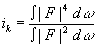
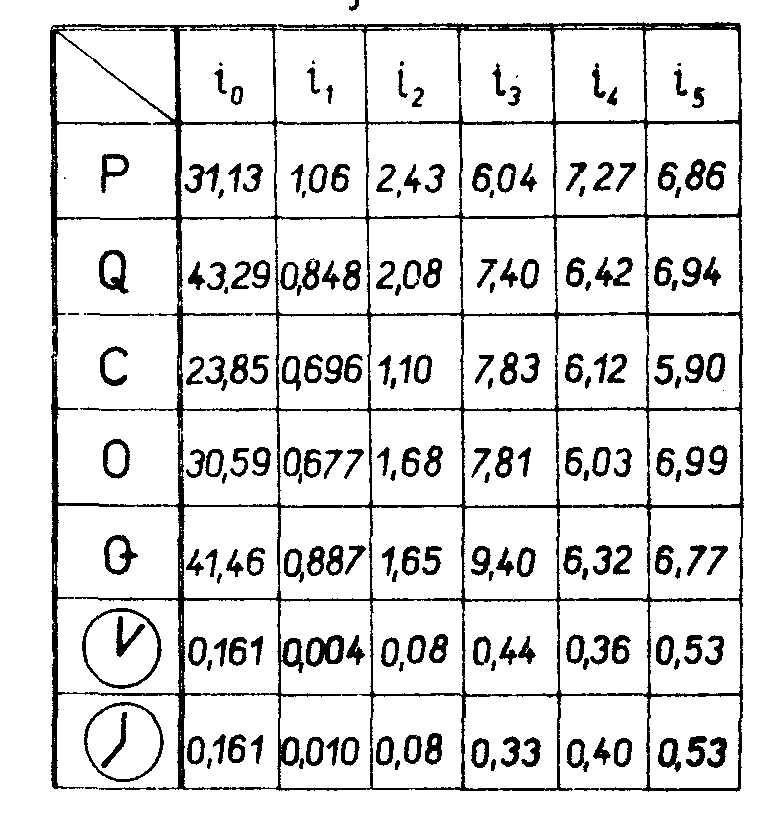
Рис.27. Значение шести информационных признаков, вычисленных на ЭВМ, для двух трековых событий и нескольких букв латинского алфавита.
Совершенно очевидно, что помехоустойчивость системы распознавания о использованием алгоритма опроса шести каналов будет выше помехоустойчивости системы о опросом только одного канала.
Преобразование Гильберта широко используется в физике и технике. Это дисперсионные соотношения в физике /14/, аналитический сигнал в техника связи /15/, огибающая и мгновенная частота речевых сигналов, фазовая коррекция в оптической спектроскопии Фурье /16/, фазовая коррекция в ЯМР спектроскопии /17/, визуализация фазовых объектов и, наконец, алгоритм распознавания с использованием гильберт-образов.
Между историями возникновения фурье-оптики и гильберт-оптики имеется много общего. Как известно, операционные методы о использованием преобразования Фурье были детально разработаны первоначально в радиофизике и теории связи, и лишь затем достижения этих областей были перенесены в оптические системы обработки информации. Плодотворные аналоги между оптикой и теорией связи широко применяется исследователями. Здесь имеется общность как математического аппарата, так и физических идей.
Между тем, фактически идеи о фурье-оптике впервые возникли еще во времена Релея, Аббе и Майкельсона, а система фильтрации в методе фазового контраста Цернике была создана без привлечения идей из радиофизики.
Развитие телевидения, радиолокации и радиоастрономии, включивших оптическое изображение в общую сеть каналов связи, способствовало тому, что вопросы оптики стали рассматриваться о общих позиций теории информации /18,19/. Наиболее решающую роль сыграли когерентные источники света и появление нового раздела прикладной оптики - голографии /1,19/ Понятия линейных систем и теория интегральных преобразований нашли в голографии новую широкую область приложения.
В настоящее время фурье-оптика как раздел современной оптики вошла в обиход широкой группы оптиков-исследователей. Язык оптика приблизился к языку радиофизика или связиста. Между тем, надо иметь в виду, что существует еще много других линейных интегральных преобразований, кроме преобразования Фурье, которые могут оказаться полезными в оптике. Второе место адесь, несомненно, отведено преобразованию Гильберта. В отличие от преобразования Фурье, которое осуществляется при помощи простого оптического элемента - высокока-
чественной собирающей линзы, преобразованиа Гильберта до последнего времени осуществлялось сложнее, чем преобразование Фурье. Можно предположить, что появление нового оптического элемента в виде дифракционной решетки со сбоем упростит реализацию преобразования Гильберта.
Следует напомнить, что оптические свойства дифракционной решетки со сбоем были известны А.Майкельсону еще в 1903 г./20/. Однако, информационное значение такого оптического элемента не было тогда замечено, и сейчас, таким образом, этот побочный эффект получил практическое применение.
Из новых областей применения дифракционной решетки со сбоем с целью осуществления преобразования Гильберта следует светить жидкие кристаллы. Наибольший интерес представляют нематические жидкие кристаллы, изменяющие свои свойства под действием электрического поля, в частности, переменного электрического поля в области частот 200-800 герц /21/. Если переменное электрическое поле приложить к тонкому слою намагниченного жидкого кристалла, заключенному между двумя стеклянными проводящими электрический ток пластинками, то жидкий кристалл приобретает структуру дифракционной решетки. Фактически в слое образуются крупномасштабные домены, и для исследователя большой интерес представляет информация о наличии разрывов и сбоев в структуре между соседними доменами и для всего поля жидкого кристалла. Основная трудность в изучении сбоев и разрывов заключается в том, что структура жидкого кристалла изменяется сравнительно быстро во времени, и фотометод оказывается бессильным. Гильберт-оптика здесь может оказаться незаменимой (рис.28). Рассмотрим простейший пример нематического жидкого кристалла, дифракционная решетка в котором состоит всего из двух крупномасштабных доменов и одной "полыньи" между ними. Если эта полынья не создает сбоя, то с помощью дифракционной решетки со сбоем будут отображены фурье-образы и гильберт-образы, которые имеют следующую структуру. Все пики дифракции света от жидкой дифракционной решетки имеют вид запоминающих кружков в поле Фурье-образа и вид разрезанных на двое "фасолинок" - в поле гильберт-образа. Если же полынья создает сбой по фазе на 180°, то картины поменяются: пики дифракции в поле Фурье-образа станут перетянутыми по середине, а пики дифракции в
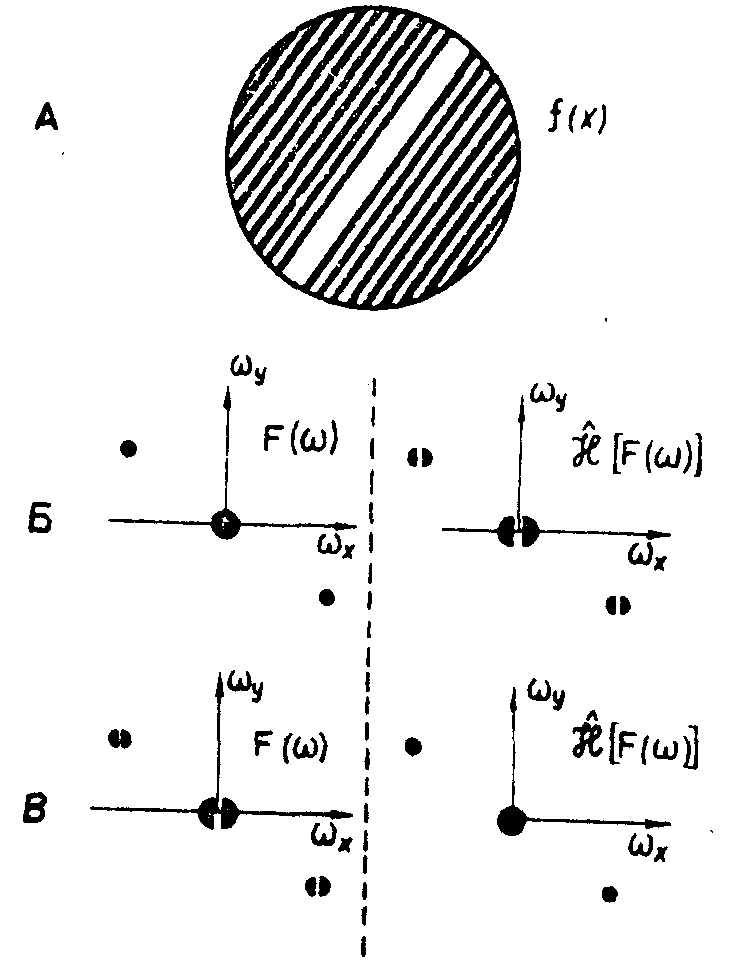
Рис.28. Пространственная картина структуры слоя нематического кристалла, помещенного в переменное электрическое поле:
а) вид жидкого кристалла в микроскоп. Видна полынья с параллельными краями;
б) вид картины, наблюдаемой с помощью дифракционной решетки со сбоем, когда "полынья" не создает сбоя;
в) то же, когда "полынья" создает сбой на половину шага жидкой кристаллической решетки.
поле гильберт-образа станут сплошными кружками.
Можно сделать общий вывод - чем больше степень антисимметрии жидкой дифракционной картины относительно линии сбоя, тем большие различия будут иметь Фурье-образ и гильберт-образ, которые отображаются одновременно с помощью дифракционной решетки со сбоем. Если перемещать линию дифракционной решетки со обоем относительно жидкого кристалла, то можно оперативно наблюдать картину Фурье-образов
и картину гильберт-образов и по ним судить об эффекте доменов и полыньей между ними.
10
Существет только один класс функция, повторное дифференцирование которых приводит нас к исходной функции, с точностью до знака. Это синусоидальные функции. Действительно,
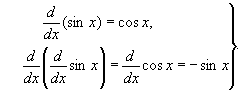 (99) (99)
Преобразование Гильберта напоминает, правда, очень отдаленно, операцию дифференцирования. В частности, для случая синусоидальных функций обе операции, преобразования Гильберта и дифференцирование, становятся просто тождественными. А именно:
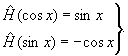 (100) (100)
Если взять функцию прямоугольный центрированный относительно точки х=0 импульс, то его гильберт-образ лишь отдаленно похож на производную от этой функции. Тем не менее, представление о преобразовании Гильберта, как о некоторой своеобразной размывающе-усредняющей операции дифференцирования, оказывается полезным. "Гильберт-дифферевдирозание" сигнала, равного "гильберт-производной" возвращает нас к исходному сигналу, независимо от того, из какого класса функций был выбран этот сигнал.
Именно благодаря такому своеобразному свойству гильберт-дифференцирования получаются предельно высокие значения оптического контраста визуализации фазового контраста с использованием фазового ножа Гильберта, так как производная от равномерного поля здесь равна нулю. Особенностью таких представлений является то, что эта производная равна нулю только в центре поля изображения, а к периферии
растет, так что основная энергия световой волны сосредоточена в узких серпиках на границе изображения.
Степень контраста визуализации фазовых объектов можно повысить, а размеры рабочей области существенно расширить, если использовать методы гашения двух волновых полей. Это может быть либо интерференция полей с противоположными фазами, либо вычитание волновых полей в скрытом изображении голографии.
Как было показано выше, волновое поле гильберт-образа плоского волнового фронта, ограниченного апертурой размером 2А, имеет
вид:
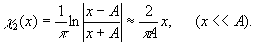
В центре кадра амплитуда этого поля растет линейно с координатой х. Так же линейно изменяется амплитуда поля гильберт-образа функции
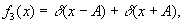
которую можно аппроксимировать двумя яркими линиями, полученными из равномерно засвеченной апертуры с помощью цилиндрической оптики. А именно, гильберт-образ этой функции равен
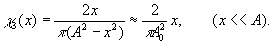
Два поля χ2(х) и χ3(х), взятые в противофазе (рис.29), дадут поле
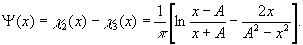 (101) (101)
Это поле было протабулировано при помощи ЭВМ. Из приведенного графика видно, что поле изображения, которое дает контраст фазовой неоднородности, равный или больше γ = 30α2 , увеличивается в этой схеме гашения с х1= 0,1 А до x2= 0,5 a, т.е. примерно в
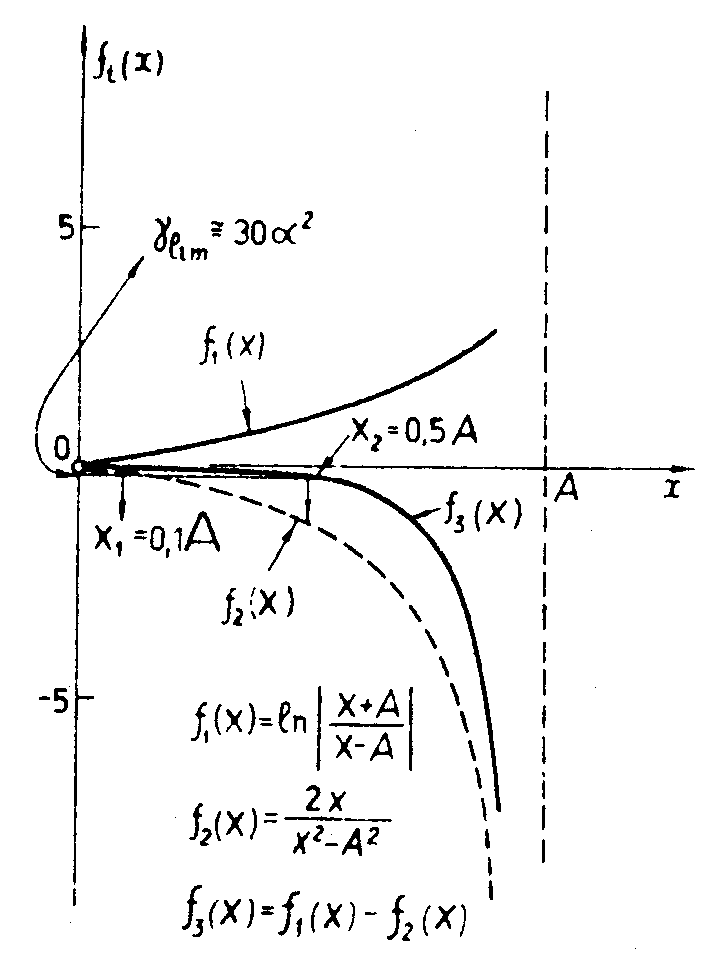
Рис.29. Эффект наложения в противофазе двух волновых полей, отображаемых дифракционной решеткой со сбоем в первом порядке дифракции. Первое волновое поле получено от апертуры размером 2А. Второе волновое поле - от узких линий. Третья кривая на рисунке соответствует результирующему полю.
Видно, что область высокого контраста расширилась, а яркость краевых серпиков возрасла.
пять раз по координате. Если также учесть, что контраст фазового ножа с использованием преобразования Гильберта выше контраста метода ножа Фуко примерно в пять раз, то чувствительность фазового ножа, в принципе, может превышать в 25 раз чувствительность метода ножа Фуко.
Метод гашения волновых полей можно применить также в методе ножа Фуко, однако из-за высокого уровня засветки трудно получать точное равенство полей в такой же степени, как это можно сделать при низком уровне засветки. Кроме этого, при гашении интенсивных полей возникают паразитные эффекты, вызванные ограниченным динами-
ческим диапазоном фотоэмульсии. Что касается методов расширения динамического диапазона, разработанных в последнее время ддя оптических систем обратной фильтрации /25/, то они являются достаточно деликатными и пока что недоступны для рядового исследователя.
Л и т е р а т у р а
1 .Л.М.Сороко. Основы голографии и когерентной оптики, "Наука и жизнь", М., 1971.
2. d.gabor,w.p.goss. interference microscope with total wavefront reconstruction. josa, 56, 849, 1966.
3. p.zernike. phasenkontrastverfahren bei der microscopishen beobachtung. zs.techn.phys., 16, 454, 1935; physik z., 36, 848, 1955.
4. М.Борн, Э.Вольф. Основы оптики, "Наука", стр.333, 1970.
5. y.belvaux, j.c.vareille. visualisation d'objects de phase par transformation de hilbert. nouv.hev.optiq.appl., 2, 3, 1971.
6. Л.А.Васильев. Теневые методы.''Наука ", 1968.
7. s.lowethal, y.belvaux. observation of phase objects by optically processed hilbert transform. appl. phys. lett., 11, 49, 1967.
8. y.belvaux, s.lowethal. white light hilbert transform. appl. opt., 10, 3, 676, 1971.
9. Л.М.Сороко, В.А.Суетин. Дифракционная решетка со сбоем как новый оптический элемент. Сообщение ОИЯИ, pi3-6565, 1972.
10. Л.М.Сороко, Т.А.Стриж, В.А.Суетин. Моделирование на ЭВМ дискретного аналога дифракционной решетки со сбоем. Сообщение ОИЯИ, pi3-6607, 1972.
11. s.j.bradskaw and p.c.child. optical data addition and subtraction. optoelectronics, 1, 1, 45, 1969.
12. a.thetford. optical addition and substraction. optoelectronics, 1, 2, 120, 1969.
13 .И.С.Гибин, А.Г.Козачок, Е.С.Невеженко, Ю.Н.Солодкин, П.Е.Твердохлеб, Ю.В.Чугуй. Анализ спектров одномерных сигналов оптическими методами. Автометрия, №1, 64-70, 1971.
14.Н.Н.Боголюбов. Б.В.Медведев, М.К.Поливанов. Вопросы теории дисперсионных соотношений, М, 1 958.
15. j.mantel. zur anwendung des analytische signals in der nachrichtentechnik, frequenz, 25, 9, 179, 1971.
16. h.sakai, g.a.vanasee. hilbert transform in fourier speotroscopy, josa, 56, 131, 1966.
17. r.h.ernst. numerical hilbert transform and automatic phase correction in magnetic resonance spectroscopy. j.magn.resonance, 1, 1, 7, 1969.
18. А.Папулис. Теория систем и преобразований в оптике, "Мир", 1971.
19. Дж.Гудман. Введение в Фурье-оптику. "Мир", 1970.
20.g.w.stroke, m.halioua. attainment of diffraction-limited imaging in high-resolution electron microscopy by "a posteriori" holographic Image sharpening. optik, 35, 50, 1972.
21.g.assouline, a.dmitrieff, m.harenp et e.leiba. diffraction d'un fasceau laser par un cristal liquide nematique soumis a un champ electrique. g.r.acad.sci., 71,16, 857, 1970.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

