coherence properties op spontaneous radiation from a large ststem of two-sevel atoms.
b.karczewski (poland)
correlation functions of the n-th order are evaluated for an arbitrary point in the far field at any instant of time t.
consider n identical atoms, located at points r1,…,rn
coupled to the quantized electromagnetic field. the atoms fill out at sane in
space whose dimensions may be large in comparision with
λ.
each atom has two nondegenerated states (±) separated
by energy hω /1/. the exciting classical pulse characterized by frequency
ω and wave vector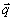 
causes the atoms to radiate. the arrival time of the pulse at the site 
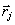is shorter than the time for spontaneous emission to start. the simulated emission
is neglected.
the hamiltonion of the system has the form
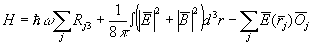
where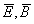 
are the electric and
magnetic field operators,
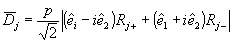
is the dipole moment operator for the j-th atom and rj±, rj3 are the energetic spin operators /1/.
the modulus of the matrix element of the dipole moment is denoted by p and
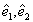are the orthogonal unit vectors
in the plane of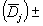 
.
in the interaction picture the electric field operators in the far zone are given by
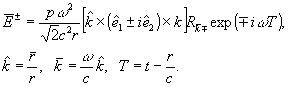
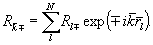(2)
the density operator of the atomic system is given as
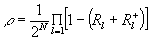(3)
where
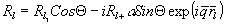
g=g(t) is a slowly varying function of time /2/.
from eqs. (2), (3) one obtains the correlation function /3/:
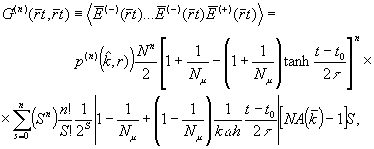(4)
where the parameter μ depends an the size and shape
/2/ of the sample, τ0 is the lifetime of single atom and
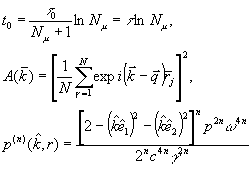
in particular, the intensity of emitted radiation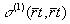 
was
evaluated in /2/. fig.1 shows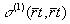
as function of time in the most interesting case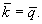 
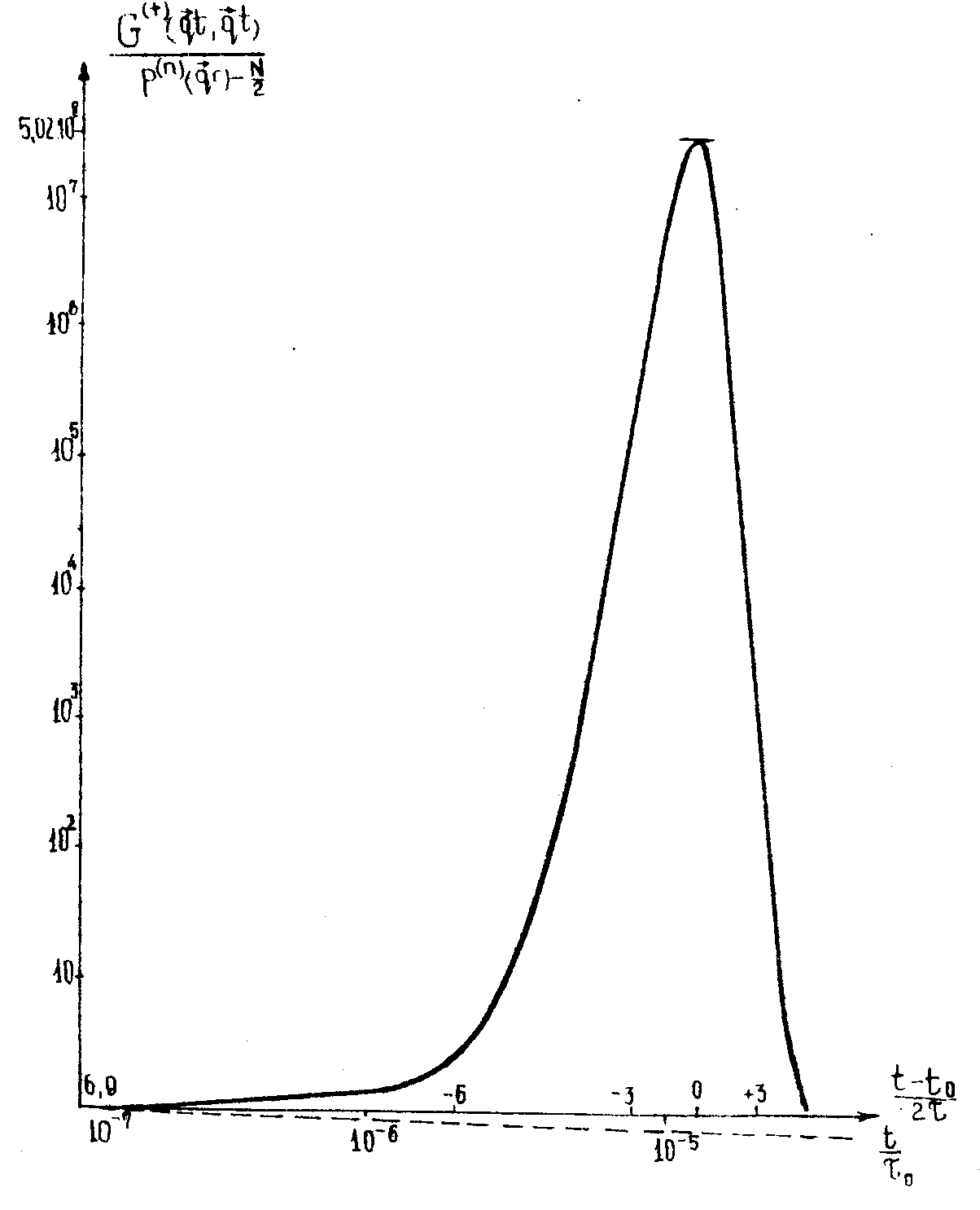
fig.1.
fig.2 shows the first four normalized correlation functions plotted versus
time for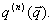 
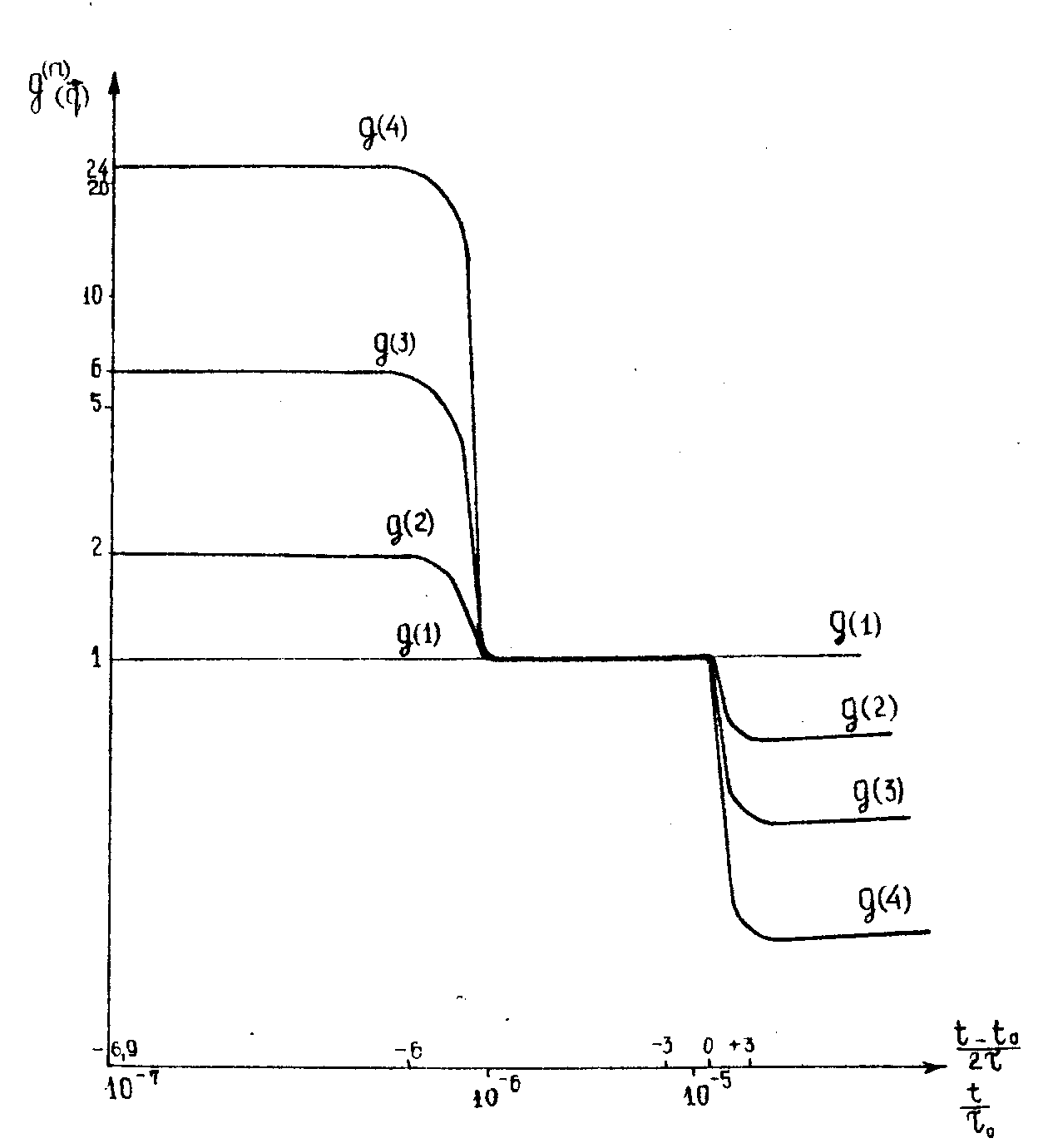
fig.2.
at the time instant t=t0 when the intensity of radiation is proportional
do n2 (the system is then said to be in the super-radiant state),
the field is completely coherent for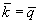 
.
for other directions itis partially coherent.
r e f e r e n c e s
1. r.h.dicke. phys.rev., 93, 99, 1954.
2. j.h.eberly, n.e.rehler. phya.rev.a.3, 1735, 1971.
3. j.chrostowski, b.karczewski. phys.lett., 35a, 121, 1971.
