|
|
 |
 |

|
| |
ФИЗИЧЕСКИЕ ПРОЦЕССЫ ЗАПИСИ И СВОЙСТВА ОБЪЕМНЫХ ФАЗОВЫХ ГОЛОГРАММ В КРИСТАЛЛАХ
С.Г.Одулов, М.С.Соскин
В работе приведен обзор экспериментальных данных по записи фазовых голограмм в электрооптических кристаллах, рассмотрены теоретические модели явления наведенной оптической неоднородности и проанализированы пути улучшения характеристик данного класса светочувствительных материалов.
В настоящее время известен целый ряд регистрирующих сред, позволяющих многократную перезапись фазовых голограмм /1/. Среди них пока что только электрооптические кристаллы обеспечивают дифракционную эффективность, близкую к теоретическому пределу для объемной фазовой голограммы η ≃100%. Возможность фиксации нестираемых светом голограмм /3, 4/ усиления записанных изображений /5/, высокая разрешающая способность (до 5000 лин/мм) /6/ и повышенная по сравнению с фотоматериалами лучевая стойкость делают этот класс светочувствительных материалов перспективным для целого ряда применений. В настоящей работе приведен критический анализ экспериментальных работ по записи голограмм в электрооптичеоких кристаллах и теоретических моделей, описывающих изменение показателя преломления в них под действием света.
Свойства голографическкх объемных решеток
в сегнетоэлектриках
Изменение показателя преломления под действием ограниченного по сечению пучка света было зарегистрировано для целого ряда монодоменизированных электрооптических кристаллов; linbo3, batio3, litao3, ktn, canb2o7, ba2nanb5o18, (sr,ba)nb2o6, srtiО3, КnbО3 /7,8/ и керамики plzt /9/. Наиболее сильные изменения проиоходили, если кристаллы вырезались перпендикулярно оптической оси и поляризация света выбиралась так, чтобы электрический вектор совпадал о осью С. При освещении кристаллов двумя пересекающими когерентными волнами в них записывалась голографическая интерференционная решетка, причем, можно было наблюдать, как самодифракцию записывающих пучков на решетке, так и дифракцию излучения с отличающейся длиной волны. Время полной записи зависит от интенсивности излучения, от величины приложенного внешнего поля (если таковое имеется) и изменяется от десятков минут при записи Неne лазером в кристалле linbo3 /10/ до секунд при записи Аr лазером в кристаллах batio3 /11/ (рис.1).
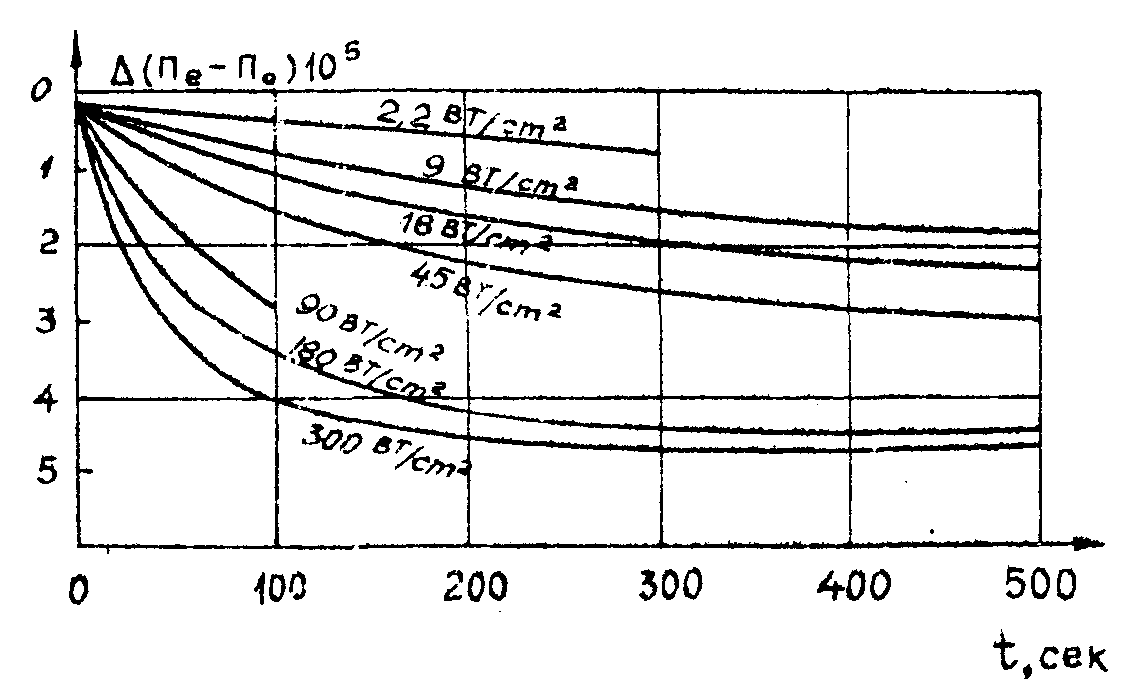
Ри c.11. Временные зависимости изменения двулучепреломления кристалла ниобата лития под действием излучения аргонового лазера.
Дифракционная эффективность голограммы определяется интансивностью облучения (рис.2), а также является функцией постоянной решетки (рис.3) /11/. В случае сред с линейным быстрооптичесчим эффектом, например, linbo3, приложение внешнего электрического поля изменяет только времена записи и стирания голограммы, не
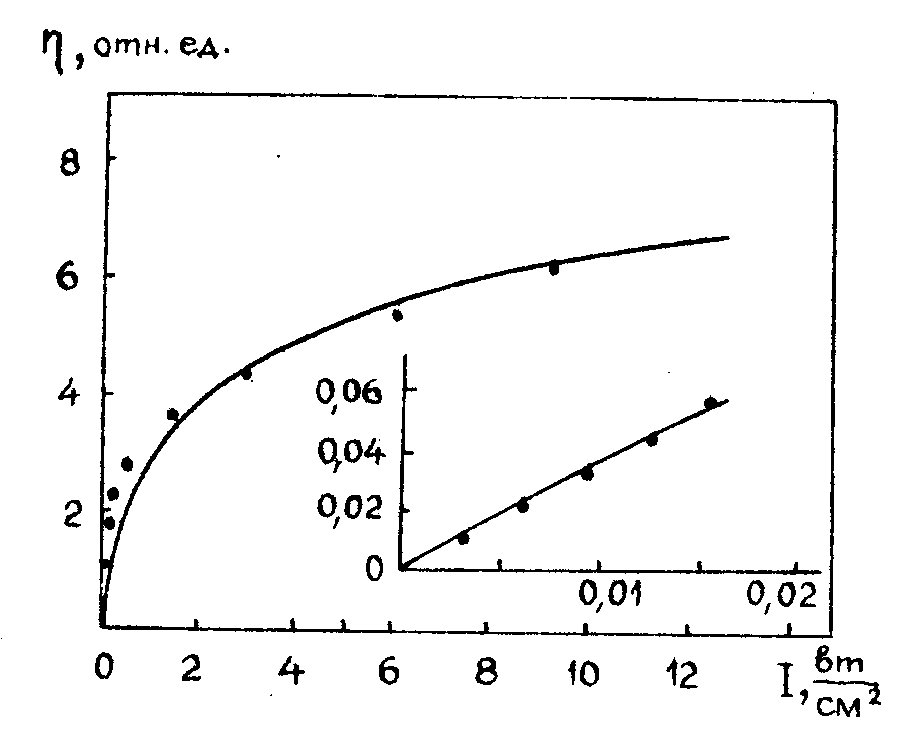
Рис.2. Зависимость дифракционной эффективности от интенсивности записывающих пучков для титаната бария.
сказываясь на величине η /10/. Для сред с квадратичным эффектом ((sr,ba)nb2o6) при помощи внешнего поля можно в достаточно больших пределах изменять значение дифракционной эффективности /12-13/,
Записанные в кристаллах голограммы сохраняются в течение определенного времени, которое сильно зависит от конкретного вещества и изменяется от нескольких недель для linbО3 /6/ до секунд для Ваtio3 /14/. Освещение кристалла однородным пучком видимого или ультрафиолетового излучения либо нагревание его значительно ускоряет процесс стирания голограммы /6/. Специальные исследования показали, что на одном и том же участке кристалла могут быть повторены, по крайней мере, двадцать раз циклы "Запись-
- полное стирание" голограммы без какого бы то ни было изменения дифракционной эффективности и скорости записи /15/ (рис.4).
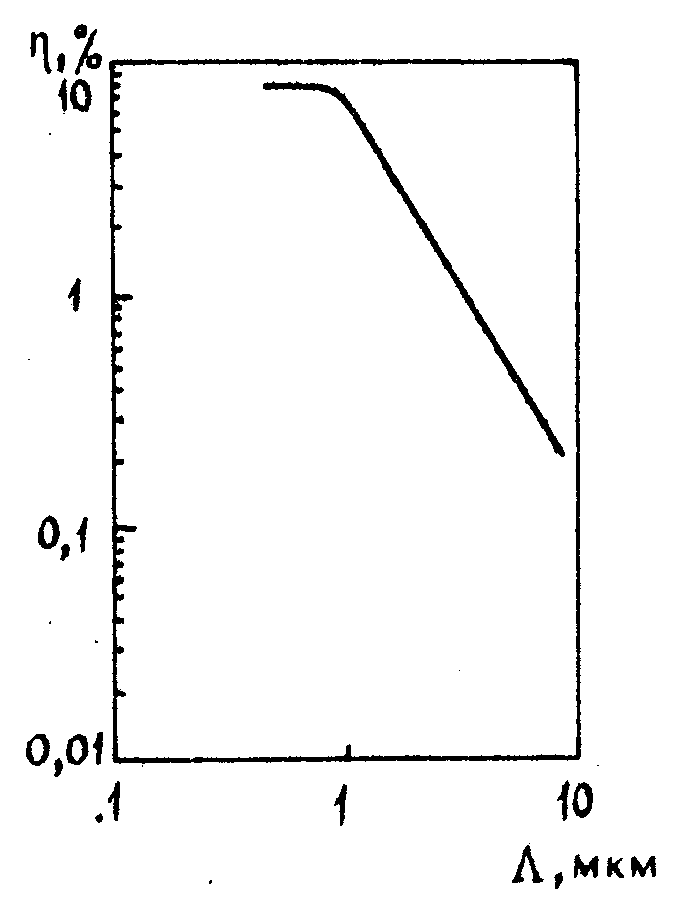
Рис.3.
Зависимость дифракционной эффективности от постоянной решетки при фиксированной интенсивности облучения.
В соответствии о теорией объемных голограмм /2/. При дифракции наблюдался только один ''-1" порядок, причем, существовала сильная угловая селективность в соответствии с формулой:
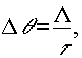 (1) (1)
где Λ - постоянная решетки, τ - толщина голограммы.
Зависимость дифракционной эффективности голограммы от глубины модуляции показателя преломления также согласуется с теоретической (см.рис.5)
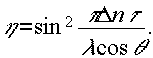 (2) (2)
В таблице приведены сравнитвльные характеристики наведенной оптической неоднородности и голографических решеток в сегнето-
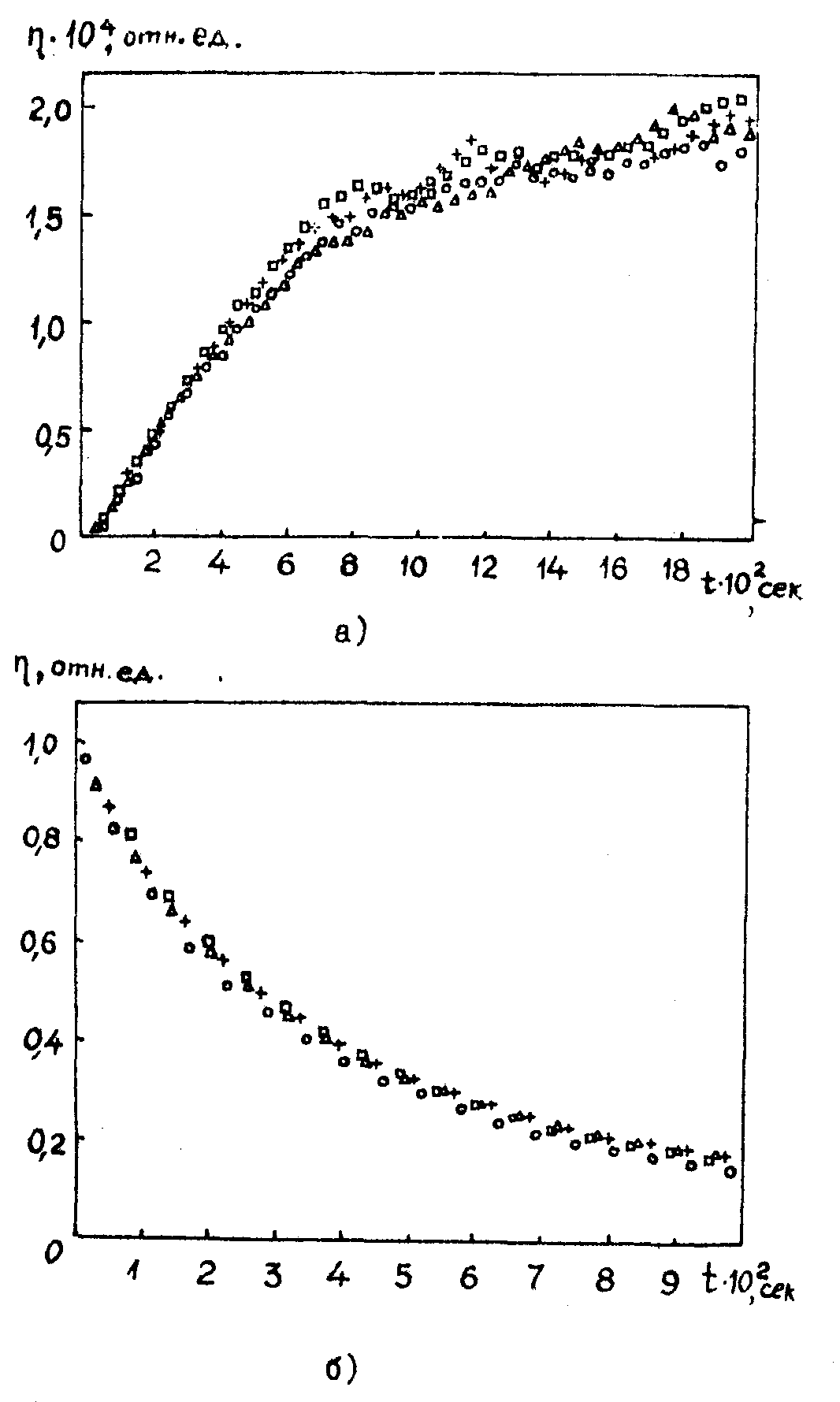
Рис.4. Временные зависимости многократных записи и стирания голограмм в ниобате лития.
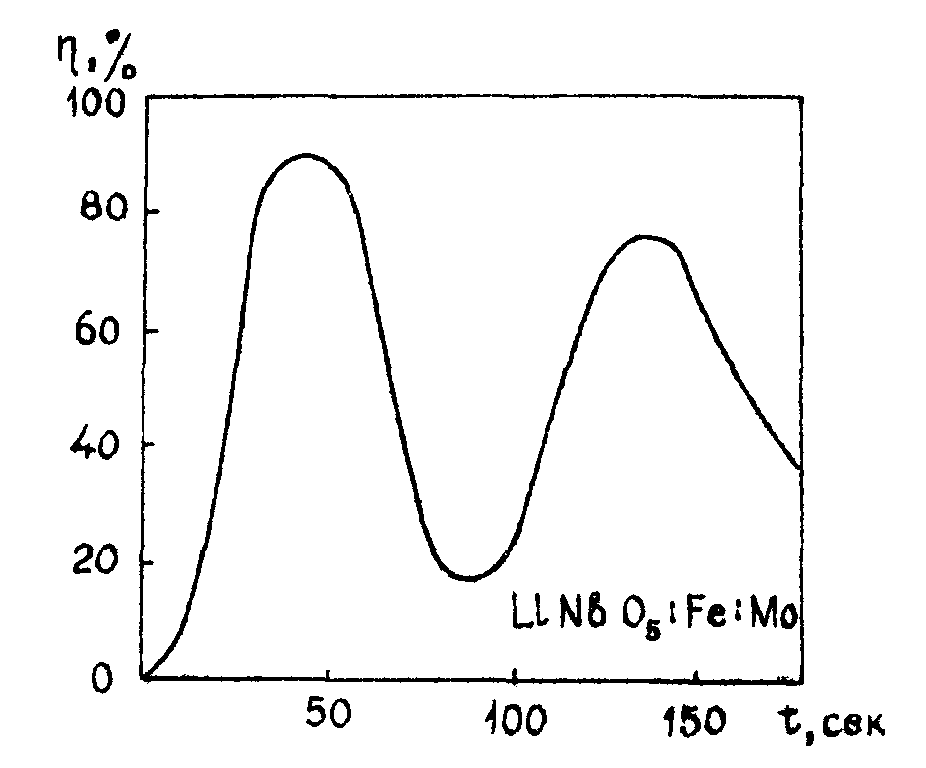
Рис.5. Зависимость дифракционной эффективности голограммы в ниобате лития, активированном 0,1 мол.% fe и 0,05 мол.% Мо .
электрических кристаллах. В колонке "Время записи" указано, также, при какой плотности облучения вто значение получено. Указанная дифракционная эффективность голограмм соответствует определенной толщине кристалла, значение которой приведено в скобках, и мощности облучения, приведенной в первой колонке. В колонке "Экспозиция" приведены вычисленные на основании данных оригинальных работ дозы облучения, требуемые для достиаэнмя дифракционной эффективности или значения Δ(ne - n0), указанной в соответсвущей колонке.
Механизм записи и теоретические модели
Изменение показателя преломления влектрооптичеоких кристаллов под действием света ("optical damage", наведенная оптическая неоднородность) связано с перераспределением объемного за-
|
Литература |
8 |
/6,10/
/21/ |
/27/ |
/28/ |
/23/ |
/41/ |
/16, 21/ |
/11/ |
|
Возможность фиксации |
7 |
100°С
В течение ~20 мин |
120°С
В течение ~5 мин |
– |
– |
– |
– |
900в В течение 0,5 сек |
|
Время записи в секундах при плотности облучения (1, вг/см 2) |
6 |
- (1)
500 (1) |
50 (5*10-2) |
7 (1) |
200 (102) |
40 (10) |
40 (1) |
5 (4) |
|
Дифракц. эффективность, r, %, при толщине решетки (τ, см) |
5 |
40 (1)
6 (0,5) |
90 (0,2) |
80 (0,25) |
60 (0,1) |
65 (0,32) |
– – |
8 (0,5) |
|
Наведенное двулуче-преломление Δ (nc-n0) |
4 |
10-3
10 |
– |
– |
– |
– |
10-4 |
– |
|
Экспозиция, дж/см 2 |
3 |
103
105 |
10 |
7,5 |
102 |
10 |
104 |
|
|
Длина волны облучения, Å |
2 |
4880
6328 |
4880 |
4880 |
6328 |
4880 |
6328 |
4880 |
|
Материал |
1 |
linbo3
-"- |
linbo3:fe |
linbo3:rh |
linbo3:cl |
ba2nanb5o15:fe |
litao3 |
batio3 |
|
8 |
/14/ |
/12/ |
/32/
/33/ |
/34/ |
|
7 |
e≈900 в В течение 0,5 сек |
e≈1100 в В течение 0,5 сек |
–
– |
– |
|
6 |
30 (1) |
60 (1) |
10 (102)
10 ( ) |
600 (10-3) |
|
5 |
5*10-2 (10-4) |
50 (0,8) |
– –
– – |
– – |
|
4 |
– |
5*10-4 |
–
5*10-4 |
4*10-4 |
|
3 |
10-3 |
14 |
103 |
104 |
|
2 |
4880 |
4880 |
6328
4880 |
4880 |
|
1 |
batio3:fe |
(sr,ba)nb2o6-(sbn) |
k(ta,nb)o3-(ktn)
-"- |
knbo3 |
ряда в образце в результате фотовозбуждения и последующего пространственного смещения электронов в зоне проводимости. В пользу такого предположения свидетельствуют заметная спектральная чувствительность материалов /16-17/ и сильное влияние статического электрического поля на скорость записи /10/. Практически все используемые кристаллы прозрачны в видимой области (ширина запрещенной зоны linbo3, например, составляет 3 эв), поэтому свет может взаимодействовать только с электронами донорной примеси, либо электронами, связанными с дефектами кристаллической решетки. Прямым доказательством существования донорных уровней в запрещенной зоне linbo3 является наблюдение видимого свечения этих кристаллов при импульсном возбуждении лазером на рубине /18/.
Перераспределение объемного заряда может воздействовать на показатель преломления двумя путями. Во-первых, при перезарядке примеси происходит локальное изменение спонтанной поляризации кристалла /8/. Во-вторых, в образцах с большим удельным сопротивлением возможно возникновение нескомпенсированных электрических полей, непосредственно изменяющих показатель преломления вследствие электрооптического эффекта /16/.
Смещение электронов в зоне проводимости также нашло два объяснения. Согласно одной модели /16/, оно связано с дрейфом в электрическом поле, другой - вызвано диффузией из-за неравномерного исходного распределения электронов /19/. Полная теория эффекта пока что отсутствует.
Попытку найти стационарное значение Δ n и описать кинетику записи на основании решения системы кинетических уравнений для свободных электронов и заполненных ловушек /11, 16, 20, 21/ нельзя признать правильной, так как в расчетах игнорировалась диффузия возбуждений и некорректно учитывалось пространственное распределение возбуждающего света. В работах /5, 10, 19/ отмечена необходимость учета диффузии возбуждений и получен ряд принципиальных качественных выводов на основании решения диффузионного уравнения. Однако, при решения принимается, что распределение электронов в зоне проводимости мало отличается от распределения интенсивности возбуждавшего света. Такое предположение приводит, в тастноотж, к парадоксальному выводу об отсутствии зависимости
глубины модуляции Δ n, от интенсивности возбуждения /19/. В последнее время высказывалось мнение, что для правильного описания эффекта необходим учет всех возможных вкладов в Δn за счет различных механизмов /22, 23/.
Определить Δ n и его временную зависимость необходимо из решения системы уравнений, в которую входят уравнение Максвелла, диффузионное уравнение и уравнения непрерывности для электронов nе и дырок nt:
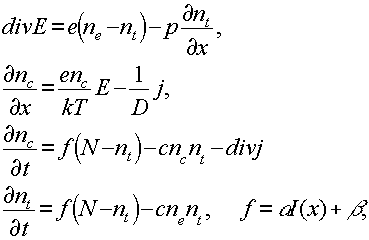 (3) (3)
где α и β - вероятности фото- и термовозбуждения электронов в зону проводимости, С - вероятность рекомбинации, р - локальное изменение поляризации при перезарядке примеси, Е - наведенное поле в образце, j - электронный ток, d - коэффициент диффузии, е- заряд электрона.
Распределение показателя преломления можно найти, если определено наведенное в образце поле Е. В стационарном случае из второго уравнения системы ( 1) получаем: */
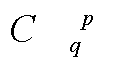 (4) (4)
причем, пространственное распределение электронов должно быть найдено из уравнения:
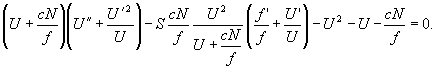 (5) (5)
Уравнение (5) нелинейное, второго порядка, точного решения в квадратурах не имеет. Приближения должны быть сделаны c учетом конкретной энергетической структуры электрооптического кристалла. Распределение электронов для не слишком глубоко залегающих примесей было указано нами в работе /24/.
Не останавливаясь на детальной исследовании уравнения (5), рассмотрим некоторые общие свойства получаемых решений. При больших иитенcивностях света:
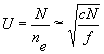 (6) (6)
и на основании (2) при 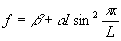 получим:
получим:
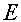 ~ ~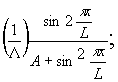 (7)
(7)
где А - постоянная, зависящая от интенсивности света и параметров кристалла.
Как видно, функция Е(х) периодическая, с тем же, что у возбуждающего света периодом
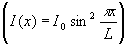 ,
однако со значительно более сложной формой штриха. ,
однако со значительно более сложной формой штриха.
Для сред с линейным электрооптическим эффектом Δ n ~ Е и, как следует из выражения (7), глубина модуляции обратно пропорциональна постоянной голографической решетки. Это позволяет объяснить наблюдавшуюся в эксперименте квадратичную вависимость дифракционной эффективности (2) от обратной постоянной решетки (см.рис.3).
Вследствие жесткой угловой селективности объемных голограмм плоская волна,
направленная на регистрирующую среду под тем же углом, что и при записи, дифрагирует
только на решетке, соответствующей первому члену Фурье разложения выражения
(7). Нетрудно видеть, что эта решетка 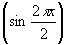 смещена относительно записывающей интерференционной картины
смещена относительно записывающей интерференционной картины 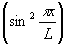 на четверть периода. Этот вывод согласуется с результатом работы /19/ и отсюда
следует возможность перераспределения интенсивности пучков, проходящих через
голограмму, в процессе ее записи (см. далее).
на четверть периода. Этот вывод согласуется с результатом работы /19/ и отсюда
следует возможность перераспределения интенсивности пучков, проходящих через
голограмму, в процессе ее записи (см. далее).
В случае квадратичного электрооптического эффекта первый
член ряда Фурье пропорционален 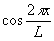 ,
таким образом, максимумы и минимумы записанной решетки совпадают с максимумами
и минимумами интерференционной картины. ,
таким образом, максимумы и минимумы записанной решетки совпадают с максимумами
и минимумами интерференционной картины.
Из точного решения можно найти зависимость глубины модуляции поля Е (а, следовательно, Δ n) от интенсивности света, оказывается, что для всех случаев Δn возрастает с увеличением интенсивности медленнее, чем по линейному закону. При этом амплитуда первого члена разложения стремится к насыщению. Эти выводы согласуются с экспериментальными результатами работ /11,16/ (см. рис.2).
Точное решение уравнения (5) содержит члены, учитывающие изменение поляризации кристалла. В результате выражение для Е становится более сложным и сдвиг записанной решетки относительно интерференционной картины в линейных электрооптических кристаллах становится меньше 90°. Чем больше относительный вклад изменения спонтанной поляризации кристалла в общее изменение Δ n, тем меньше сдвиг решетки. Учет изменения спонтанной поляризаций несколько видоизменяет также зависимость Δn от интенсивности, однако, зависимость дифракционной эффективности от постоянной решетки остается той же самой (7).
Методы улучшения записывающих материалов
Поскольку описанные модели изменения Δn предполагают наличие примерно 1018 - 1020 см донорных центров, можно утверждать, что это не неконтролируемая примесь в чистых кристаллах. С другой стороны, известно, что концентрация кислородных вакансий в этих кристаллах может достигать 1019 см-3 /25/, а в расстехио-метрированных кристаллах возможно образование дефектов такой же концентрации, связанных с избытком ниобия /8/. В настоящее время вопрос о природе дефектов окончательно не выяснен. Исследования зависимести величины наведенной оптической неоднородности от стехиометрического состава в кристаллах ниобата и танталата лития /21/ показало, что эффект усиливается по мере уменьшения содержания ионов ниобия (рис.6). Это позволяет предположить, что дефекты, приводящие к изменению Δn, связаны скорее с кислород-
ными вакансиями, чем с ионами ниобия.
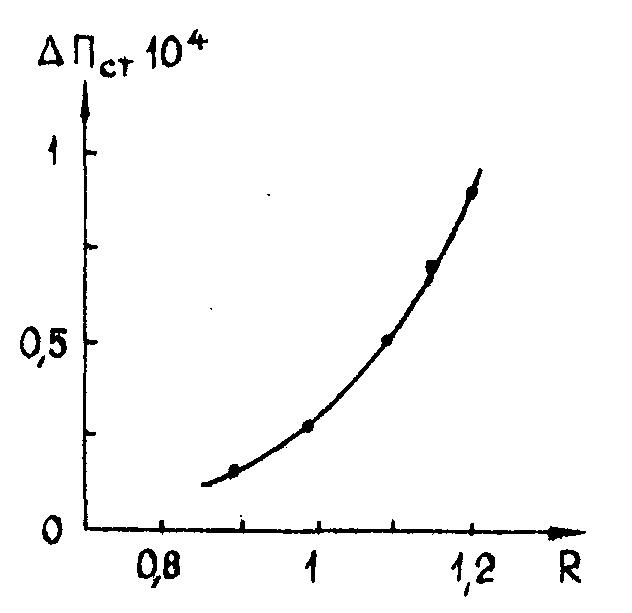
Рис.6 .
Зависимость стационарного изменения показателя преломления под действием света с фиксированной интенсивностью от стехиометрического состава кристаллов танталата лития.
Так как запись связана с наличием достаточной концентрации подходящих донорных центров, были проведены исследования кристаллов с искусственно созданными центрами. При этом ставилась задача улучшения двух основных характеристик: чувствительности материала и дифракционной эффективности голограмм. Было использовано γ - облучение образцов и специальное легирование кристаллов.
В результате γ - облучения ниобата лития (106 рад, 12 Мэв, кобальтовая пушка) в спектре поглощения кристалла появлялась дополнительная полоса в сине-зеленой области /26/ что свидетельствовало об образовании новых центров. На рис.7 показаны зависимости эффективности голограммы от времени при записи для одного образца до и после γ - облучения. Чувствительность увеличилась примерно в 20 раз, дифракционная эффективность возрасла почти на порядок.
Этот метод улучшения характеристик записывающего материала пригоден не для всех электрооптических кристаллов. Облучение кристаллов ba2nanb5o15, например не приводит к изменению чувствительности. Связано это с тем, что в различных материалах γ - облучение создает дефекты с различающимся энергетическим спектром и не все из них дают вклад в изменение показателя преломления.
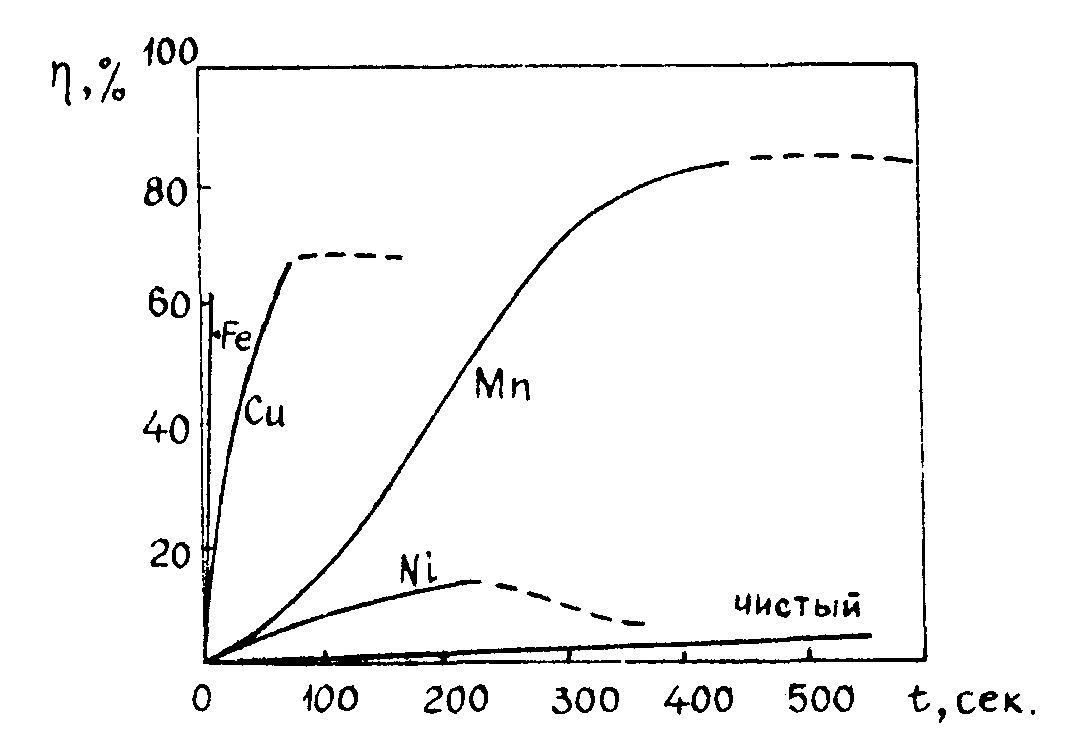
Рис.7. Сравнительные характеристики записи в чистых и активированных кристаллах ниобата лития.
Второй метод, позволяющий направленно влиять на тип и концентрацию донорных центров в кристалле, заключается в выращивании легированных кристаллов. Сравнительные характеристики записи в кристаллах ниобата лития, активированных ионами fе, Сu, Мn, ni, показаны на рис.8. Видно, что наиболее удобным активатором является ион железа, использование которого повышает чувствительность более, чем на два порядка /27/. Существенное улучшение параметров голограмм в кристаллах ниобата лития наблюдается также при легировании ионами rh /28/ и Сl/25/ в активированных кристаллах была получена рекордная дифракционная эффективность голограммы порядка 90% ( linbo3 : fe /26/ и ba2nanb5o15 /27/). Однако, необходимо заметить, что многие активированные кристаллы обладают заметным поглощением, на длине волны аргонового лазера коэффициент поглощения linbo5 : rh составляет 10 см-1. В таких случаях наиболее выгодно считывание записанных голограмм в другой спектральной области, где поглощение не так существенно.
Чувствительность кристаллов титаната бария также возрастает примерно на два порядка при легировании ионами железа /14/. Обна-
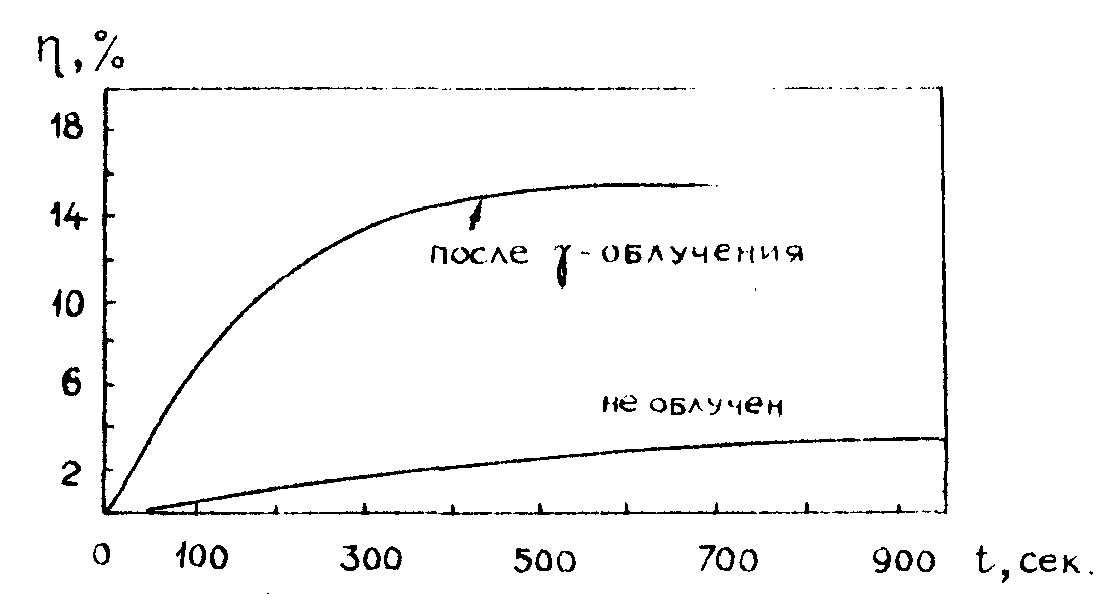
Рис.8. Временные зависимости дифракционной эффективности голограмм в кристалле ниобата лития до и после γ - облучения.
ружено, что существует оптимальная концентрация, при превышении которой дифракционная эффективность голограмм вновь снижается. Чувствительность batio3 возрастает также при легировании ионами Мо, но, как для linlo3 /1/, она снижается при избыточном содержании ионов ниобия.
Фиксация голограмм
Стирание голограмм при считывании позволяет производить запись в динамическом режиме. Однако, в ряде случаев необходимо создавать нестираемые светом голограммы. В настоящее время известны два способа фиксации голограмм. Оба они сводятся к созданию неравновесного пространственного распределения донорных центров в кристалла.
Первый метод включает термическую обработку кристалла с записанной голограммой. При комнатной температуре ионная проводимость linbo3 с στ≲10-9 см-1 Ω-1, подвижность ионов ничтожно
мала, и решетка в кристалле записывается только вследствие диффузии и дрейфа электронов. При повышении температуры можно достичь области, в которой подвижность ионов становится уже существенной, но вероятность тепловых забросов в зону проводимости еще достаточно мала. При нагревании кристалла с записанной голограммой до такой температуры заряженные ловушки начинают мигрировать с тем, чтобы скомпенсировать наведенное при записи электрическое поле. Дифракционная эффективность при этом уменьшается до нерегистрируемого значения. Если затем охлажденный образец вновь освещать однородным пучком, голограмма "проявляется", причем, значение η, начиная с некоторого момента, уже не зависит от времени (рис.9). Восстановление связано с тем, что число фотопереходов, пропорциональное распределению донорных центров, не является после отжига равномерным по кристаллу.
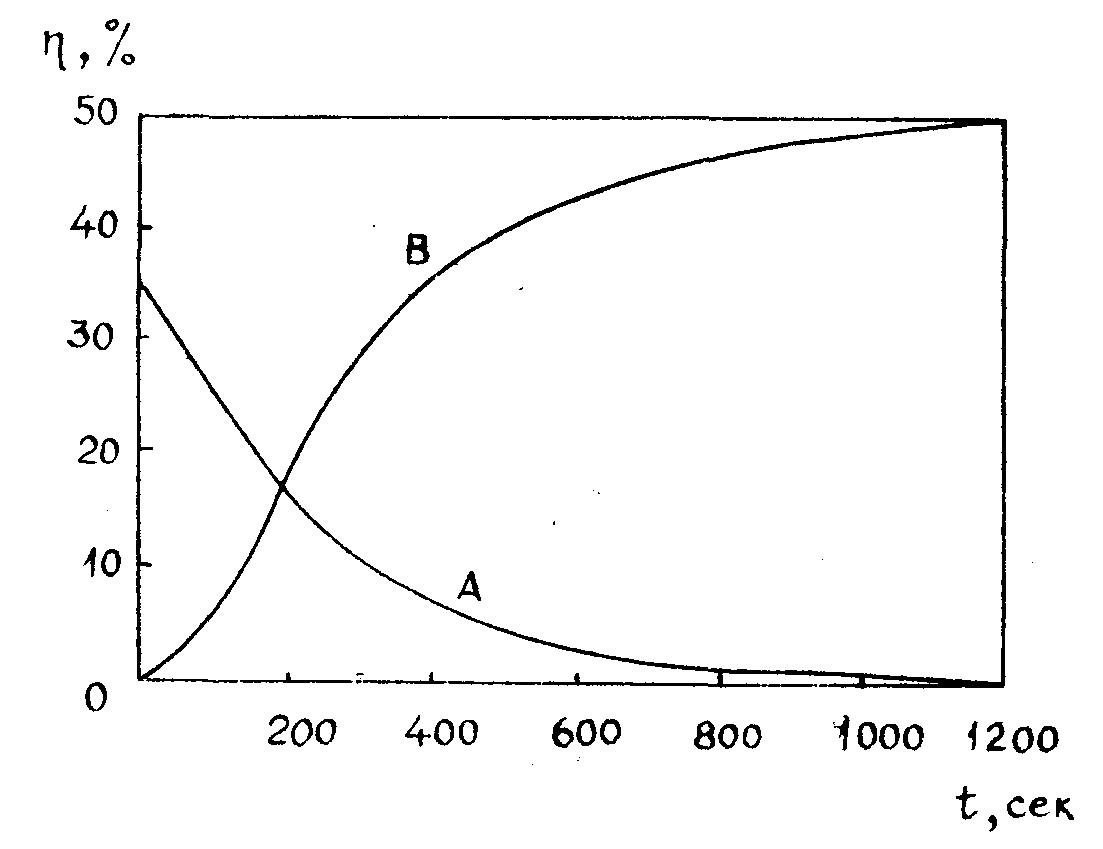
Рис.9. Временные зависимости оптического стирания голограммы в кристалле ниобата лития (А) и восстановления фиксированной голограммы одним из записывающих пучков (Б).
Предельное значение η, до которого "проявляется" фиксированная голограмма, зависит от направления считывающего луча по отношению к полярной оси кристалла и может быть как выше, так и ниже η исходной голограммы. Этот эффект является следствием записи сдвинутой по отношению к интерференционной картине решетки и будет рассмотрен в следующей разделе.
Второй способ был использован для фиксации голограмм в кристаллах ba0.25sr0.75nb2o6, batio3 и состоял в приложении внешнего электрического поля, напряженностью порядка величины коэрцитивного поля в данном кристалле (Е≃0,9 кв для Ыbn и Е=1,1 кв для Ваtio3). Длительность воздействия долина быть вполне определенной; при меньших длительностях происходит неполный сдвиг положительных ловушек, при слишком больших голограыма становится нестабильной: достигается большее значение η, но затеи происходит стирание.
Фиксированная в кристалле голограмма может бить стерта обычный образом при нагревании кристаллов до определенной температуры (170°С для linbo3). Воздействие ультрафиолетовым излучением приводит к частичному уменьшению дифракционной эффективности фиксированной голограммы в linbo3, однако повторное "проявление" однородным пучком света, направленным под тем же углом, что и при записи исходной голограммы, восстанавливает фиксированную голограмму до преднего значения η.
Эффекты перераспределения интенсивности
В стационарных условиях дифракция на динамической решетке, возникающей в среде, показатель преломления которой линейно зависит от интенсивности воздействующего света (n(x) = n0 + n2|e|2) на приводит к изменению интенсивности двух записывающих пучков, прошедших сквозь голограмму /29,30/. b линейных электрооптических кристаллах изменение n таково, что записываемая решетка оказывается сдвинутой по отношению к интерференционной картине на некоторый угол ф. Интенсивность опорного и предметного пучков ir и is на выходе голограммы в этом случае /5/:
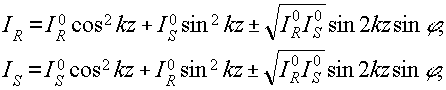 (8) (8)
здесь 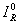 и
и 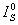 - исходные интенсивности опорного и предметного пучков,
z - толщина голограммы, k=πΔnλcosθ.
Ηнак последнего члена в каждом
равенстве определяется направлением полярной оси кристалла. Таким образом, в
процессе записи голограммы в кристалле интенсивность одного пучка увеличивается
за счет ослабления другого. При θ = 90° возможно полное суммирование интенсивности
обоих падающих пучков в одном выходящем.
- исходные интенсивности опорного и предметного пучков,
z - толщина голограммы, k=πΔnλcosθ.
Ηнак последнего члена в каждом
равенстве определяется направлением полярной оси кристалла. Таким образом, в
процессе записи голограммы в кристалле интенсивность одного пучка увеличивается
за счет ослабления другого. При θ = 90° возможно полное суммирование интенсивности
обоих падающих пучков в одном выходящем.
Экспериментальное наблюдение эффекта перераспределения интенсивности двух пучков при записи голограммы (рис.10) является подтверждением диффузионного характера записи голограмм в неактивированном кристалле ниобата лития / 5/. Сравнение экспериментальных стационарных значений отношения ir и is и дифракционной эффективности η позволяет по формулам (2,8) определить точное значение угла рассогласования φ. Оценки для чистых кристаллов linbo3, сделанные по данным работы /5/, дают значение φ, близкое к 90°. Проведенные нами эксперименты показали, что для кристаллов linbo3, нестехиометрического состава (r=li/nb≈1,2) и кристаллов, активированных церием, значение φ значительно меньше 90°, причем, оно зависит от контраста записывающей интерференционной картины (рис.11).
Перераспределение интенсивности пучков на сдвинутой решетке приводит к интересному эффекту самоусиления фиксированных голограмм. Заключается он в том, что эффективность фиксированной голограммы может быть выше эффективности исходной голограммы при соответствующем выборе считывающего пучка. При освещении отожженной при 100°С голограммы одним из записывающих пучков в результате фотопереходов создается неравновесное пространственное распределение электронов и возникает голограмма. В результате дифракции появляется второй пучок, причем, картина интерференции вновь оказывается сдвинутой относительно фиксированной решетки. Поэтому в зависимости от направления считывающего пучка интенсивность диф-
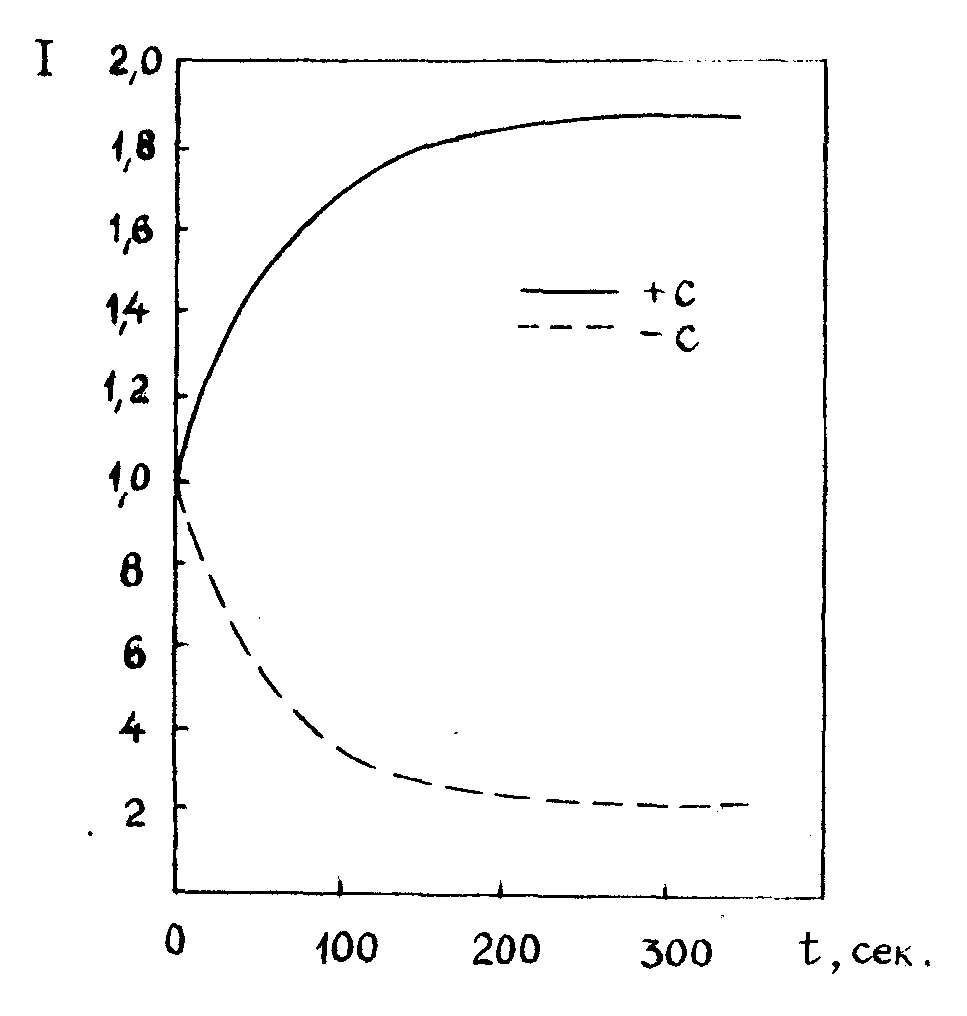
Рис.10. Изменение интенсивности двух, прошедших сквозь кристалл ниобата лития, пучков света в процессе записи голограммы.
рагированного луча может либо возрасти, либо уменьшиться по сравнению с нефиксированной голограммой.
По данным работы /31/ слабое перераспределение интенсивности пучков при записи наблюдалось также в кристаллах ниобата лития, легированных железом, что также является подтверждением записи в них сдвинутых решеток.
3 а к л ю ч е н и е
С момента появления первых работ по оптической записи в электрооптических кристаллах этому классу регистрирующих сред предска-
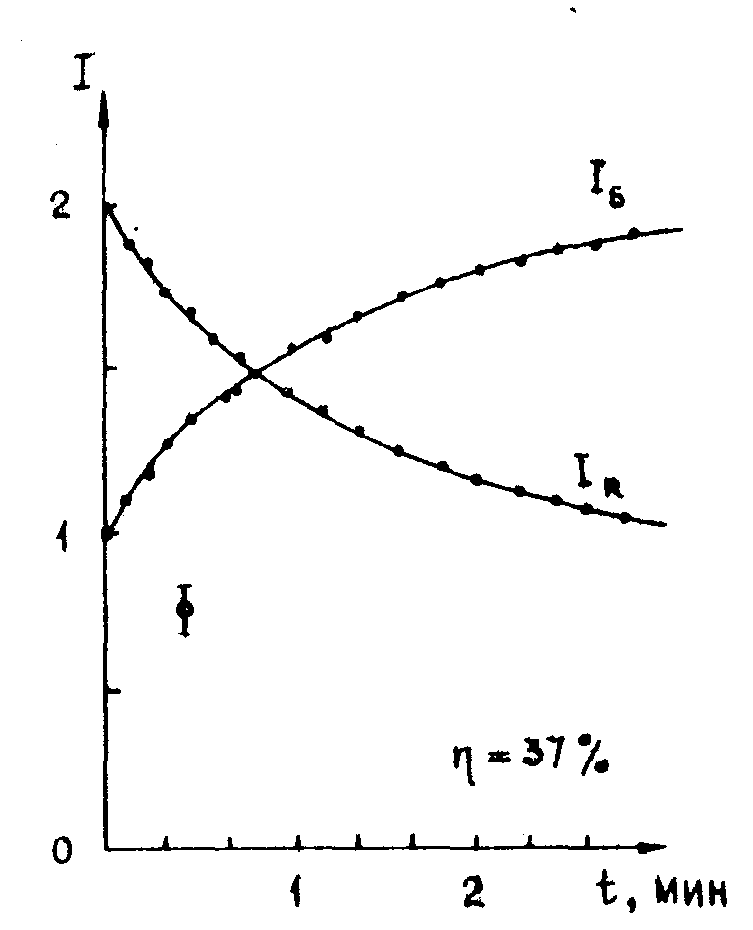
Рис.11. Изменение интенсивнооти двух прошедших пучков света при записи голограммы в образца расстехиометриоованного ниобата лития ( r=li/nb≈1,2). Исходное отношение интенсивностей пучков 2:1
зывали большое будущее. Уже сообщалось о записи цветных объемных голограмм в активированных кристаллах ниобата лития. Возможность управления чувствительностью кристаллов на различных длинах волн позволила синтезировать кристаллы, в которых запись и воспроизведение осуществляется при помощи трехцветного лазера на смеси аргона и криптона (4880, 5145 и 6471) Å. Разработка новых усовершенствованных материалов и техники фиксации нестираемых голограмм значительно расширяют сферу возможных применеий. Использование для динамической записи оперативной и долговременной памяти, создание голографических оптических элементов - далеко не полный пе -
речень направлений, в которых ведутся интенсивные работы.
В то же время сейчас еще нельзя считать исследования голографической записи в электрооптических кристаллах завершенными. Необходимо многое сделать как для развития теории эффекта, так и для усовершенствования самих материалов, причем, наиболее важной задачей является сокращение времени записи и стирания голограмм.
Л и т е р а т у р а
1. j.bordogna, s.keneman, j.amodei. rca rev., 33, 227, 1972.
2. h.kogeknik. bstj, 48, 2909, 1969.
3. j.j.amodei, d.l.staeblere. appl.phys.lett., 18, 540, 1971.
4. f.misheron, g.bismuth. appl.phys.lett., 20, 79, 1972.
5. b.l.staebler, j.j.amodei. j.appl.phys., 43, 1042, 1971.
6. f.s.chen, j.t. lamacchia, d.b.fraser. appl.phys.lett., 13, 223, 1968. .
7. a.ashkin et al. appl.phys.lett., 9, 72, 1966.
8. w.d.johnston. j.appl.phys., 41, 3272, 1972.
9. f.micheron et al. С.r.acad.sc., serie В, 274, 361, 1972.
10. j.j.amodei, d.l.staebler. rca rev., 33, 71, 1972.
11. r.l.townsend, j.t.lamacchia. j.appl.phys., 41, 5188, 1970.
12. j.b.taxter. appl.phys.lett., 15, 210, 1969.
13. f.micheron, j.bismuth. appl.phys.lett., 41, 5188, 1970.
14. f.micheron, g.bismuth. j. de physique, supl.33, c2-149, 1972.
15. t.k.gaylord, t.a.rabson, f.k.tittel. appl.phys.lett., 20, 47, 1971.
16. f.s.chen. j.appl.phys., 40, 3389, 1969.
17. h.b.serzeze, r.b.goldner. appl.phys.lett., 22, 626, 1975.
18. a.hordvik, h.schlosberg. appl.phys.lett., 20, 197, 1972.
19. j.j.amodei. appl.phys.lett., 18, 540, 1971.
20. f.micheron, g.bismuth. optics communs., 3, 390, 1971.
21. Н.Б.Ангерт, В.А.Пашков, Н.М.Соловьева. ЖЭТФ, 62, 1666, 1972.
22. v.e.wood. j.appl.phys., 44, 1391, 1975.
25. С.Г.Одулов. М.С.Соскин. УФЖ, 18, 1037, 1973.
24. М.Ф.Дейген, В.Б.Марков, С.Г.Одулов, М.С.Соскин, Б.Д.Шанина. Спектроскопия диэлектриков и процессы переноса, сб.рефератов конференция "Физика диэлектриков...". Изд.НИИ ЛНПО "Позитрон", 40, Л., 1973.
25. k.nassau, m.e.lines. j.appl.phys., 41, 533, 1970.
26. j.j.amodei, w.phylips, d.l.staebler. appl.optics, 11, 390, 1972.
27. w.phylips, j.j.amodei, d.l.staebler. rca rev., 33, 94, 1972.
28. a.ishida, o.mikami, s.miyazawa, m.sumi. appl.phys.lett., 21, 192, 1972.
29. Б. Я.Зельдович. Краткие сообщения по физике, ФИАН, m., № 5,1970.
3 0. Ю.А.Ананьев. Письма в ЖЭТФ, 18, 000, 1973.
31. t.k.gaylord, t.a.rabson, f.k.tittel, c.r.quick. j.appl.phys., 44, 896, 1973.
32. f.s.chen. j.appl.phys., 38, 3418, 1967.
33. s.r.king, t.s.hartwick, А.В.chase. appl. phys. lett., 21, 312, 1972.
34. d.ostrovski, o.royer, e.spitz. compt.rend., 270, 540, 1971.
33. j.j.amodei, d.l.staebler, a.w.stephens. appl.phys.lett., 18, 507, 1972.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

