|
|
 |
 |

|
| |
ПОЛЯРИЗОВАННЫЙ СВЕТ В ГОЛОГРАФИИ И МЕТОД ПОЛЯРИЗАЦИОННОЙ ЗАПИСИ
Ш.Д.Какичашвили
Рассматривается математический аппарат, используемый для описания поляризованного света. Показана информационная недостаточность известных методов голографической записи векторного поля.
Рассматривается новый вид голографической записи - поляризационная запись, позволяющая фиксировать состояние поляризации суммарного (объектного + опорного) поля в виде переменной по поверхности голограммы анизотропии, основан ная на Вейгерт-эффекте.
В параксиальном приближении показано восстановление векторного поля объекта при реконструкции с подобной голограммы для случая наведенного светом чистого двулучепреломления.
Как известно, электромагнитные волны поперечны. Для описания поперечного характера колебаний световых волн принято рассматривать изменение во времени картины проекции вектора поля на перпендикулярную лучу плоскость. Для изотропных сред электрический и магнитный векторы ортогональны и подобное описание электромагнитного поля является полным. Предпочтение электрического вектора связано с его преобладающей ролью в процессах взаимодействия света с веществом.
В общем случае электрический вектор когерентного света описывает эллипс, и свет называется эллиптически поляризованным. При этом проекционная картина имеет вид эллипса, описываемого тремя параметрами: азимутом проекции α (углом между большой осью а с осью х), эллиптичностью β (отношением полуосей эллипса b/a ) и
направлением вращения электрического вектора по часовой стрелке (вправо) и против часовой стрелки (влево). В частности, линейно поляризованный свет имеет бесконечное число возможностей ориентации азимутов проекции, эллиптичность, равную нулю, и неопределенный характер вращения. Свет циркулярно поляризованный имеет неопределенный азимут проекции, эллиптичность, равную единице, и два возможных состояния вращения вправо или влево.
Для гармонической векторной волны, являющейся решением векторного волнового уравнения, электрический вектор можно положить равным /1/:
 (1) (1)
где 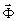 (x,y,z)
- комплексный вектор координат (x,y,z)
- комплексный вектор координат
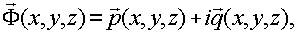
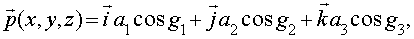
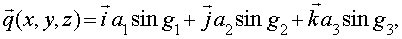
а 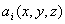 -
проекции амплитуды на соответствующие оси координат; -
проекции амплитуды на соответствующие оси координат; 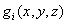 - скалярные функции координат, характеризующие
форму волны.
- скалярные функции координат, характеризующие
форму волны.
Для плоской векторной волны, распространяющейся вдоль оси z, имеем
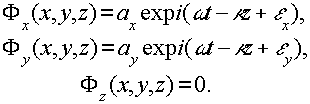 (2) (2)
В этом случае поляризованную волну представляют столбцом из двух элементов, называемым полным вектором Джонса /2/:
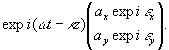 (3) (3)
Для определения характера поляризации векторной волны вычисляются вспомогательные величины;
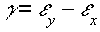 ; ; 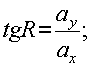
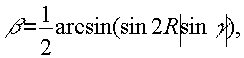 (4) (4)
откуда следует азимут главной оси
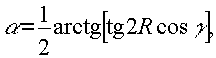
эллиптичность
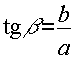
и характер вращения:
правый при sinγ > 0,
левый при sinγ < 0 .
Использование вектора Джонса удобно для вычисления результата сложения ряда плоских когерентных пучков с произвольным характером поляризации. Для этого последовательно складываются соответствующие элементы столбцов векторов, что дает вектор Джонса суммарной волны.
Для описания оптического устройства, через которое проходит когерентный поляризованный свет, наиболее удобно матричное представление, развитое также Джонсом. Устройство описывается 2х2 матрицей и позволяет вычислить результат взаимодействия света с этим устройством. В отличие от обычных тригонометрических и алгебраических методов метод Джонса чрезвычайно прост и компактен, что особенно важно для вычисления результата прохождения света через совокупность различных поляризующих устройств.
При определении матрицы Джонса исходят из обычного описания поляризованной плоской волны и математическим путем определяют те изменения, которые возникают при введении на пути пучка данного поляризующего устройства /3,4/. Матрицы Джонса для большинства известных поляризующих устройств получены в ряде работ /5/. При использовании метода Джонса необходимо перемножить все матрицы стоящих на пути света устройств справа налево таким образом, что матрица самого последнего устройства оказывается расположенной слева, и результат перемножить на вектор Джонса входящего пучка.
В качестве примера рассмотрим прохождение ориентированного под 45° линейно поляризованного света через совокупность линейной фазовой пластинки с азимутом оси наибольшей скорости 0° и линейного поляризатора с азимутом оси пропускания -45° (ортогонально поляризации входящего света). Для полного вектора Джонса получим:
 (5) (5)
где d1, d2 - толщины соответствующих элементов; n0, ne, n -соответственно, коэффициенты преломления для обыкновенного и необыкновенного луча фазовой пластинки и коэффициент преломления линейного поляризатора. Как и следовало ожидать, (5) описывает линейно поляризованный луч с ориентацией плоскости колебания ортогонально входящему.
В общем случае волны произвольного характера, возникающей при рассеянии на неоднородном анизотропном экране, необходимо использовать векторную форму дифракционного интеграла Кирхгофа, который в точке наблюдения р имеет вид /6/:
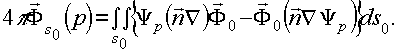 (6) (6)
Здесь s0
-область, занятая рассеивающим экраном, с контуром Г; 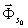 - возмущенное на s0
векторное поле в точке р;
- возмущенное на s0
векторное поле в точке р; 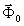 - невозмущенный произвольный вектор, удовлетворяющий векторному уравнению Гельмгольца:
- невозмущенный произвольный вектор, удовлетворяющий векторному уравнению Гельмгольца:
 (7) (7)
причем, компоненты Фо,х ,Фо,у, Фо, z удовлетворяют соленоидальным условиям:
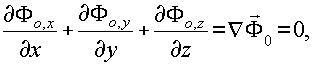 (8) (8)
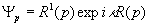 - -
вспомогательная функция. После ряда преобразований /6/ получается выражение,
одновременно удовлетворяющее уравнениям Максвелла:
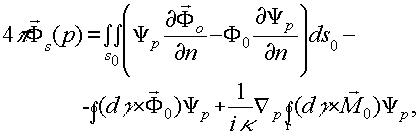 (9) (9)
где 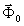 и
и 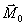 -векторные поля, связанные, соответственно, с электрическим и магнитным вектором
просвечивающего света непосредственно за дифрагирующим экраном;
dγ -
элемент контура.
-векторные поля, связанные, соответственно, с электрическим и магнитным вектором
просвечивающего света непосредственно за дифрагирующим экраном;
dγ -
элемент контура.
Если область s0
достаточно велика и точка наблюдения удалена, то пренебрегая двумя последними
интегралами, а также изменением 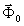 вдоль
вдоль 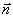 ,
можно получить векторный интеграл Кирхгофа в параксиальной форме, аналогичной
форме Зоммерфельда в скалярной теории /7/: ,
можно получить векторный интеграл Кирхгофа в параксиальной форме, аналогичной
форме Зоммерфельда в скалярной теории /7/:
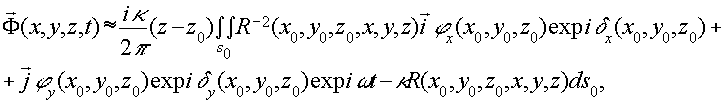 (10) (10)
где 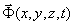 - поле в точке наблюдения х, y, z;
- поле в точке наблюдения х, y, z; 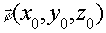 -поле за рассеивающим экраном с координатами
х0
-поле за рассеивающим экраном с координатами
х0, y 0, z 0; 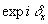 и
и 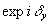 - распределение начальной фазы для соответствующих компонентов электромагнитной
волны непосредственно за экраном. Однако, следует особо подчеркнуть, что если
контур Г является существенно переменным не только на краях экрана, но и внутри
его, то приближение (10) оказывается недостаточно точным. Тем не менее, параксиальная
форма (10) может быть модифицирована таким образом, что учет компонентов электрического
вектора луча дифрагированного
- распределение начальной фазы для соответствующих компонентов электромагнитной
волны непосредственно за экраном. Однако, следует особо подчеркнуть, что если
контур Г является существенно переменным не только на краях экрана, но и внутри
его, то приближение (10) оказывается недостаточно точным. Тем не менее, параксиальная
форма (10) может быть модифицирована таким образом, что учет компонентов электрического
вектора луча дифрагированного
экраном в произвольном направлении оказывается частично возможным.
Примем очевидное допущение сохранения состояния поляризации луча при дифракции /8/. Тогда, если до дифракции компоненты электрического вектора поляризованной волны в собственной системе координат х', у' , z' (где в качестве z' выбрано направление распространения) суть φx', φy', , то идее сохранения поляризации при дифракции в направлении l, m , n будет соответствовать "жесткий" поворот собственной системы координат, определяемый следующей таблицей направляющих косинусов (рис.1).
|
x' |
y' |
z' |
|
x |
l1 = 1-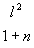
|
l2 = 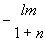
|
l3 = l |
|
y |
m1 = 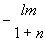
|
m2 = 1-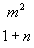
|
m3 = m |
|
z |
n1 = -l |
n2 = -m |
n3 = n |
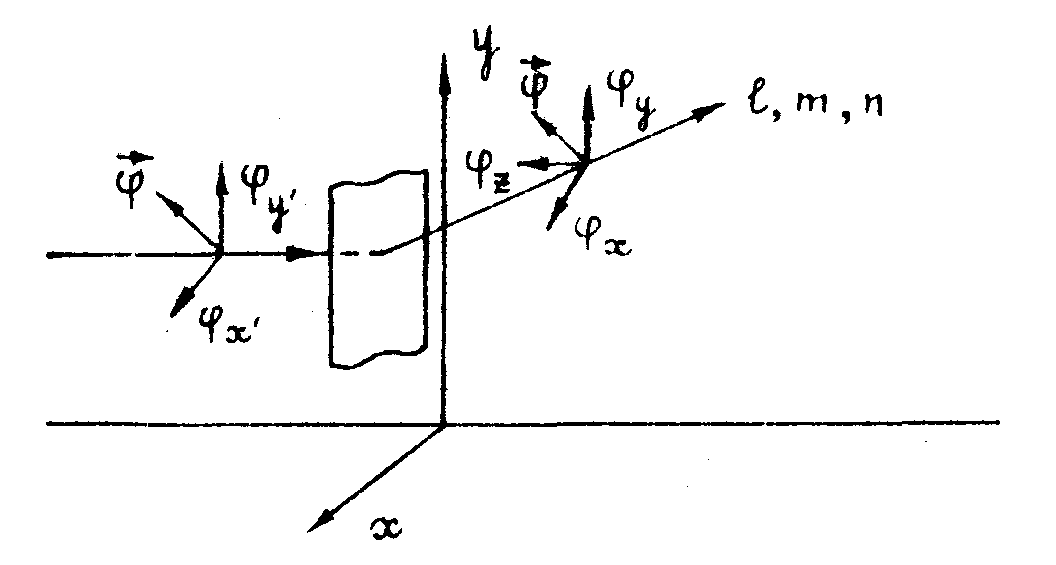
Рис.1.
В результате такого поворота компоненты электрического вектора отклоненного луча выражаются в виде:
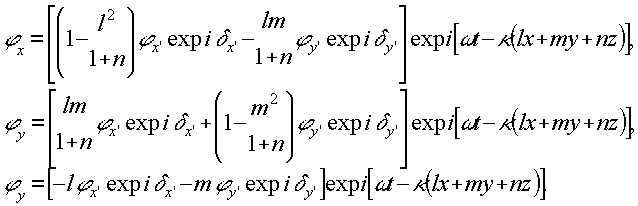 (11) (11)
Если плоский дифрагирующий экран произвольного характера анизотропии расположен нормально к просвечивающей волне, то следует использовать метод Джонса для нахождения волны непосредственно за экраном и использовать принцип сохранения поляризации при дифракции уже для этой волны. Вводя трехкомпонентный вектор Джонса для описания электрического вектора произвольно ориентированного луча, можно формально написать:
 (12) (12)
где φ x, φy, φz - компоненты электрического вектора дифрагированного луча; φx', φy', 0 - компоненты просвечивающей волны; первая из 9-компонентной матрицы описывает "жесткий" поворот; вторая же является матрицей Джонса, описывающей переменную по поверхности экрана анизотропию. Подставляя полученное выражение (12) в параксиальную формулу Кирхгофа окончательно получаем вырадение для дифрагированного векторного поля, которое может найти разнообразные применения:
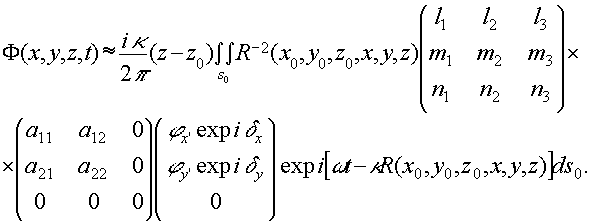 (13) (13)
Здесь
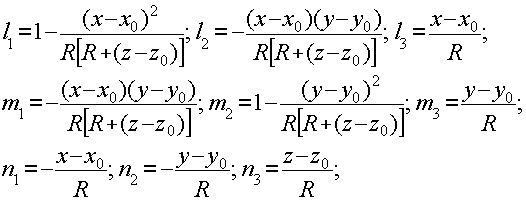 (14) (14)
а элементы матрицы дифрагирующего экрана aij(x,y,z) суть функции координат x, y, z. Интеграл (13) для большинства практически важных случаев легко решается в асимтотическом приближении (см., например /1/).
Используя развитый здесь математический подход, рассмотрим голографическую запись и реконструкцию точечного источника сферической электромагнитной волны /9-12/.
На рис. 2 s 0 -
точечный источник света, интерферирующий с плоской опорной волной  .
Пусть результат интерференции фикси- .
Пусть результат интерференции фикси-
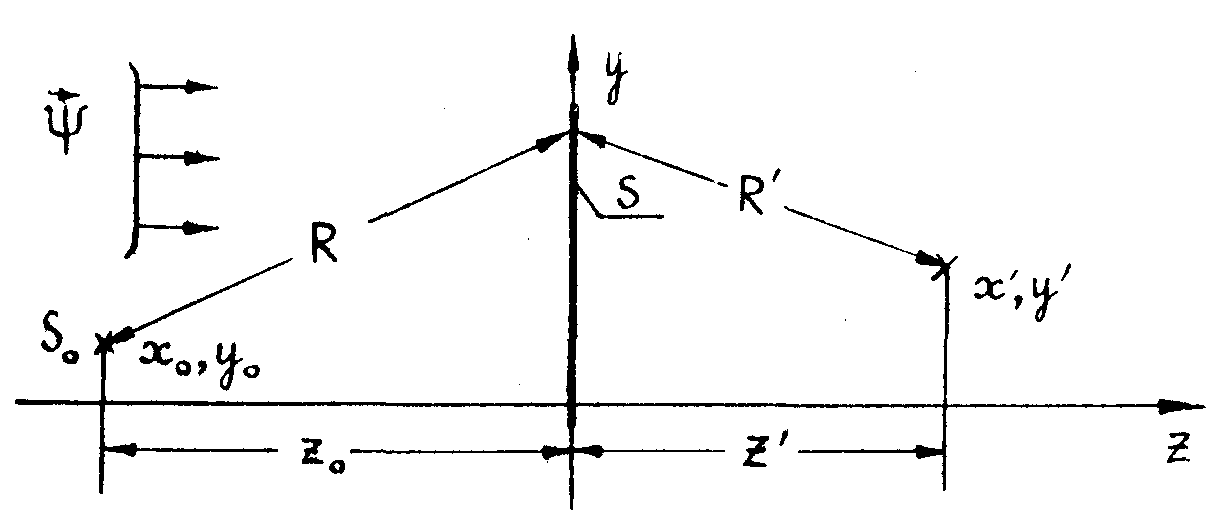
Рис.2.
руется на светочувствительной поверхности s в плоских z=0. Суммарное поле имеет вид:
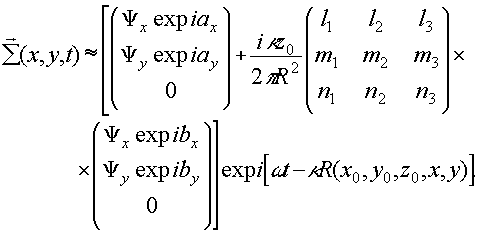 (15) (15)
Примем постулируемое скалярной теорией голографической записи утверждение, что фиксируемой на светочувствительном материале является плотность электрического поля:
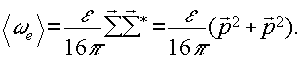 (16) (16)
Для нашего случая
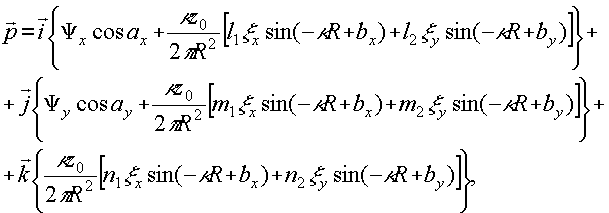
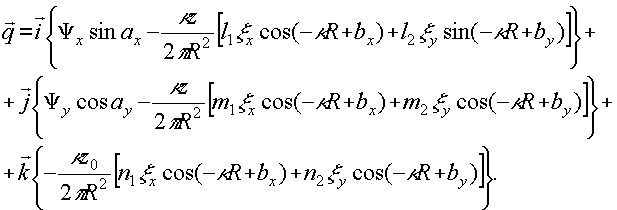
Полагая амплитудную прозрачность полученной голограммы равной
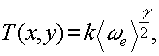
где k - коэффициент, связанный с сенситометрической характеристикой материала. Выбрав для простоты γ=2, имеем:
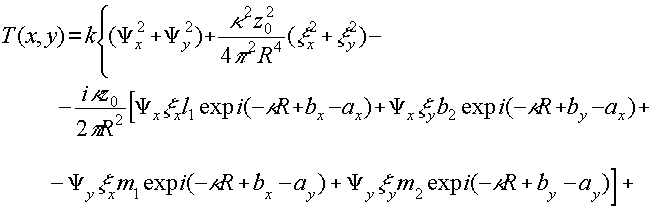
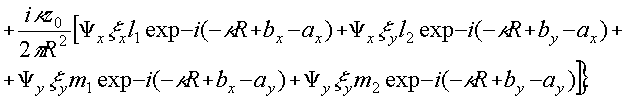 (17') (17')
Воспользуемся (13) и вычислим дифрагированное прозрачностью ( 17') поле в точке x', y', z':
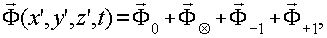 (18) (18)
где
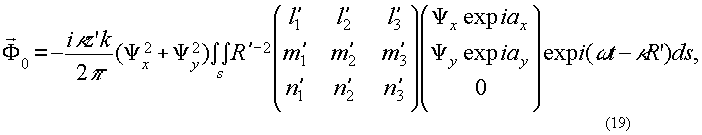

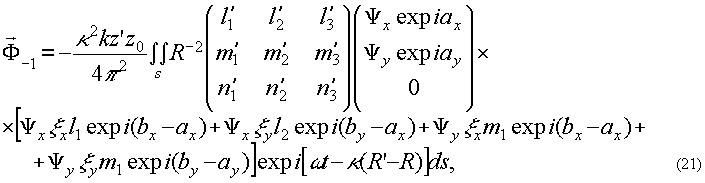
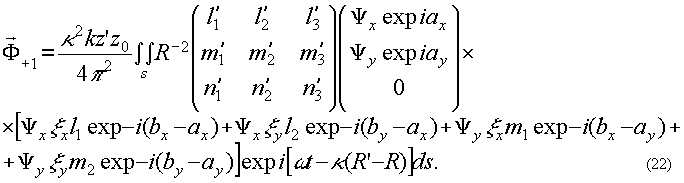
В асимптотическом приближении, используя метод стационарной фазы, получаем
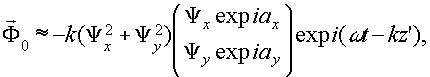 (19') (19')
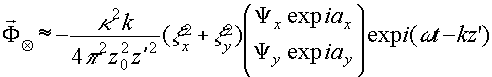 (20') (20')
и, полагая x'=x0, y'=y0,
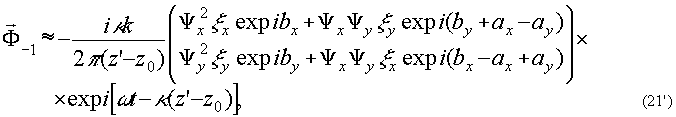
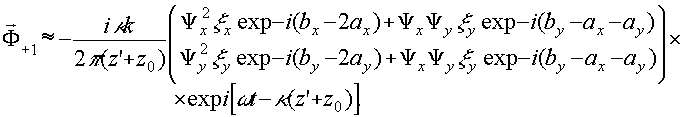 (22') (22')
Анализ полученных членов показывает, что (19 ') описывает часть реконструирующей волны, прошедшей через голограмму без дифракции. (20') связано с амплитудами опорной и объектной волн и оно распространяется в том же, что и (19') направлении. (21') и (22') описывают, соответственно, мнимое и действительное изображения точечного объекта. Анализ состояния поляризаций реконструированного мнимого (так же как и действительного изображения) показывает, что оно не соответствует поляризации исходного объекта и фактически является поляризационным сравнением объектной волны с опорной. Как и следовало ожидать, в частном случае взаимноортогональных состояний поляризации объектной и опорной волн реконструированные компоненты (21') и (22') полностью исчезают.
Подобное положение дел, очевидно, связано с тем, что матрица дифрагирующей прозрачности Т(х,у) в нашем случае вырождена в простой скаляр. По-видимому, для существенно полной голографической записи необходимо каким-либо образом смоделировать и зафиксировать на голограмме кроме интенсивности суммарной волны так же ее состояние поляризации. В этом случае наша голограмма будет описываться 2х2 матрицей и будет способна полностью реконструировать векторный характер рассеянного объектом электромагнитного поля. Поскольку состояние поляризации - величина наблюдаемая, то подобная запись оказывается принципиально возможной и была экспериментально осуществлена /15/. В эксперименте для моделирования состояния поляризации было использовано явление наведения анизотропич при взаимодействии фиксируемой волны с веществом.
Пусть энергетический спектр ансамбля атомов (молекул) в основном состоянии содержит два подуровня 1, 2. Соотношение насе-
ленностей между этими подуровнями может быть изменено множеством различных способов, из которых нас будут интересовать изменения, вызванные светом резонансной частоты ν 1,3, который переводит атом из 1 в 3, откуда при спонтанном переходе к 1 и 2 меняется установившаяся заселенность этих уровней. Подобное изменение заселенности всегда сопровождается изменением ориентации моментов атомов и в зависимости от характера поляризации возбуждающего света ν1,3 и магнито-механических моментов атомов может происходить вдоль или против приложенного поля. Явления ориентации атомов и молекул под воздействием света наблюдаются как в газообразных, так и в твердых телах /14/. Аналогичные явления имеют место в молекулярных фотохимических системах, время жизни которых в возбужденной состоянии, вызванном квантом резонансного поглощения, чрезвычайно велико. Различными искусственными способами это состояние может быть зафиксировано на практически неограниченное время. Подобные явления в материальных светочувствительных средах впервые наблюдались Вейгертом /15/ и в дальнейшем были обнаружены и исследованы рядом авторов в различных красителях и кристаллах /16,17/. В них под воздействием поляризованного света участок светочувствительного вещества приобретает анизотропию с ориентацией оптической оси параллельно или антипараллельно плоскости колебания электрического вектора воздействующего света.
В зависимости от используемого фотоанизотропного вещества голографическая запись может быть проведена по любой из классических схем /9,10/. Мы рассмотрим голографическую запись на светочувствительном веществе, приобретающем под воздействием поляризованного когерентного света наведенное двулучепреломление (анизотропно-базовая запись).
Пусть имеется плоская, линейно поляризованная опорная волна, падающая нормально к светочувствительной поверхности s, установленной в начале координат
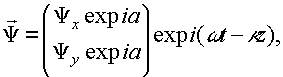 (23) (23)
а также волна пространственно переменной поляризации, рассеянная достаточно удаленным объектом s0. в параксиальном приближении
можно, с достаточной для наших целей точностью, положить
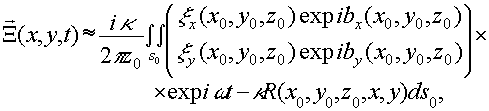 (24) (24)
где 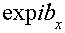 , , -распределение
комплексной амплитуды по поверхности объекта; -распределение
комплексной амплитуды по поверхности объекта; 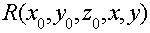 -
расстояние до точки наблюдения х, у, 0. В плоскости светочувствительной поверхности
суммарное поле есть -
расстояние до точки наблюдения х, у, 0. В плоскости светочувствительной поверхности
суммарное поле есть
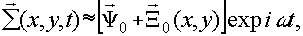 (25) (25)
где  -
комплексные векторные функции координат. Очевидно, для суммарного электрического
вектора имеем -
комплексные векторные функции координат. Очевидно, для суммарного электрического
вектора имеем
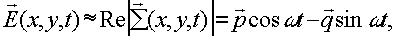 (26) (26)
где
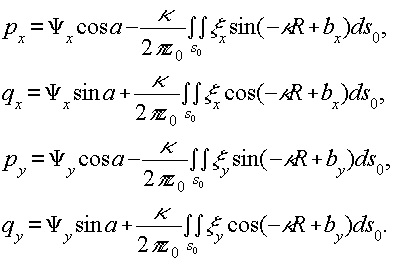
Из (26) следует, что конец электрического вектора с течением времени описывает эллипс.
В отличие от записи в скалярной теории голографии, мы принимаем возможность фиксации двух основных характеристик светового эллипса: величин квадратов полуосей и их ориентацию. Поскольку эти величины являются наблюдаемыми, подобное допущение вполне естественно.
Выразим в явном виде значения квадратов полуосей светового эллипса (26) и их ориентации относительно исходной системы координат:
 (27) (27)
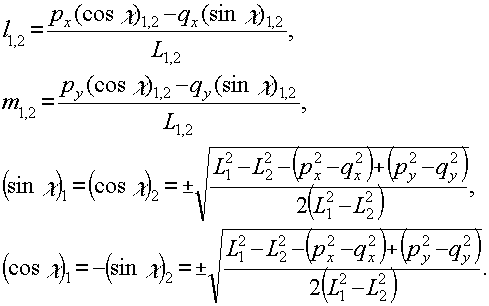 (28) (28)
Здесь 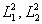 - соответственно, квадраты большой
и малой полуосей светового эллипса, a l1, m1
и l2, m2 - их
направляющие косинусы.
- соответственно, квадраты большой
и малой полуосей светового эллипса, a l1, m1
и l2, m2 - их
направляющие косинусы.
Под воздействием суммарного поля светочувствительный центр материала, обладающего вейгерт-эффектом, деформируется неодинаково вдоль большой и малой осей светового эллипса. Мы положим, что деформация является упругой, и применим обобщенный механический закон Гука для плоского напряжения, связывающий деформацию с напряжением σ /18/:
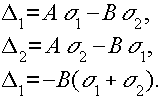 (29) (29)
Полагая, что под воздействием поля изменение коэффициента диэлектрической проницаемости фотоанизотропного вещества с исходным ε 0 подчиняется аналогичному закону, имеем
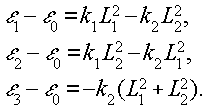 (30) (30)
При k1=k2=k, где k - постоянная материала, получаем для главных показателей преломления
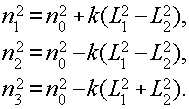 (30') (30')
Сконструируем эллипсоид волновых нормалей /1/ для элементарного участка голограммы в системе координат ξ ', η', ζ', ориентированной вдоль осей эллипсоида:
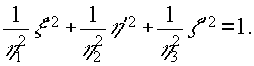 (31) (31)
Для нахождения прозрачности этого участка при просвечивании лучом нормально к поверхности проведем сечение эллипсоида плоскостью голограммы z=0. Полуоси полученного при сечении эллипса дадут икомые, неглавные коэффициенты преломления η'1, η'2 элементарного двулучепреломляющего участка. В системе координат, параллельной x, y, z, имеем два эллипса
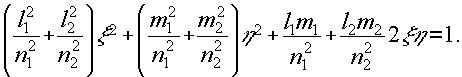 (32) (32)
Воспользуемся нормированной матрицей Джонса, описывающей двулучепреломляющий кристалл /5/. Полагая (η '1-η'2) достаточно малым (слабое наведение двулучепреломления), ограничимся линейным приближением матрицы:
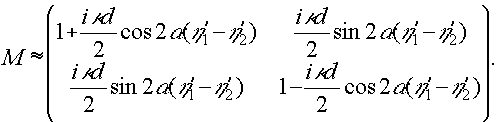 (33) (33)
Здесь α - угол оси η '1 с х; d - толщина двулучепреломляющей голограммы. Используя простые соотношения приведения эллипса к каноническому виду, получаем
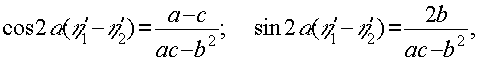 (34) (34)
Где а, с, b - коэффициенты, соответственно, при ξ2, η2, 2ξη σравнения (32). Используя (34) и (26), окончательно получаем матрицу, описывающую зафиксированное на голограмме двулучепреломление, наведенное суммарным светом:
 (33') (33')
Просветим голограмму реконструирующим светом, совпадающим с опорным. Сформированное за голограммой в точке x', y', z' поле в параксиальном приближении есть
 (35) (35)
Подставляя значения px, qx, py, qy из (26), получаем
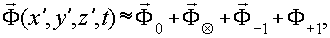 (36) (36)
где
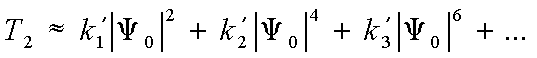 (37) (37)
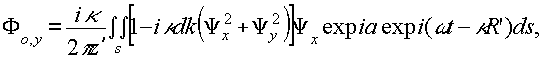
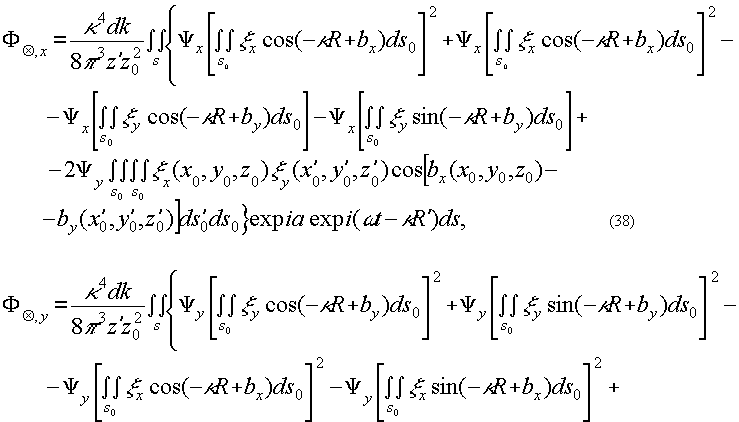
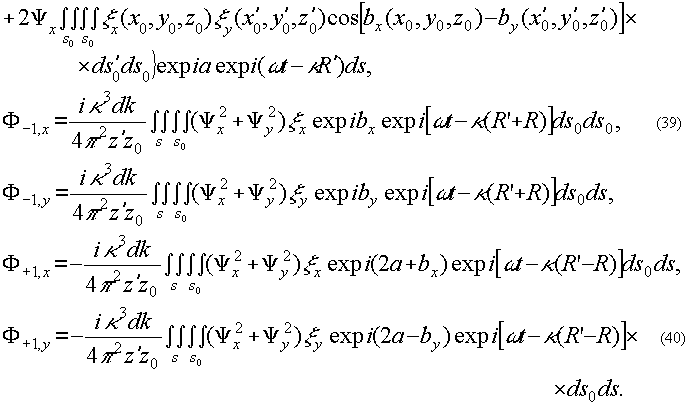
Вычислим выражения (37), (38), (39), (40) а асимптотическом приближении ( s0→±∞, s→±∞). Предварительно, обратив порядок интегрирования, в квадратичном приближении для расстояний r и r' получим внутренние интегралы искомых выражений:
 (41) (41)
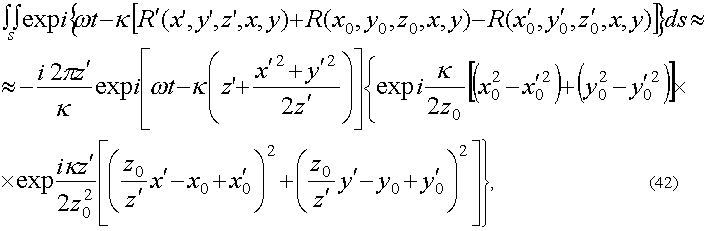
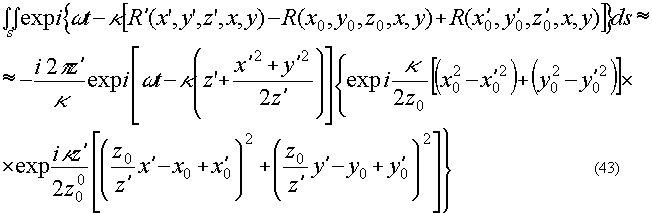
при z'=-z0
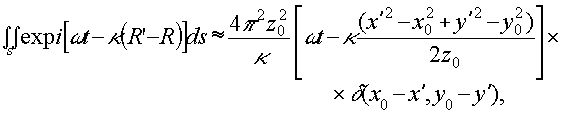 (45) (45)
где δ (x0 - x',y0 - y') - импульсная δ-τункция. Подставляя полученные интегралы в (37), (38), (39), (40), получаем
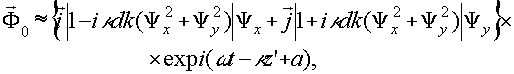 (37') (37')
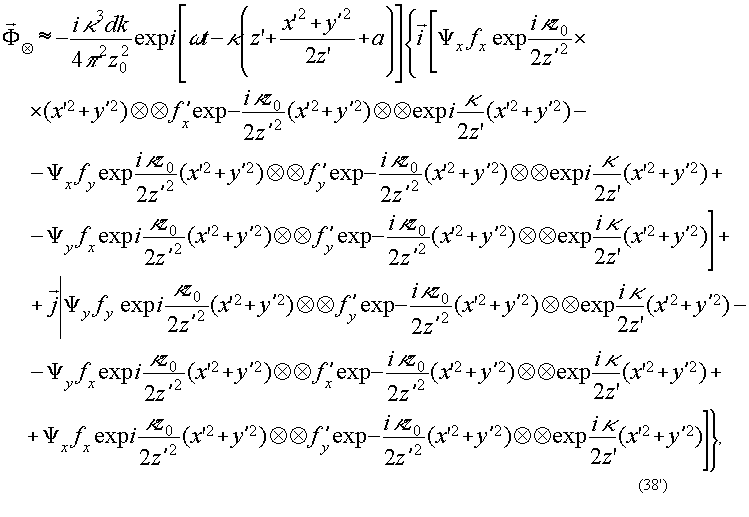
где символ 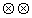 означает
двумерной свертки /19/ и введено обозначение означает
двумерной свертки /19/ и введено обозначение
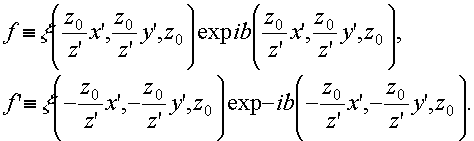
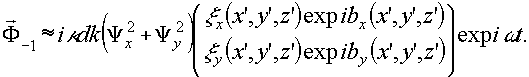 (39) (39)
 (40) (40)
Из (37') следует, что в первом члене разложения (36) информации об объекте
не содержится. Этот член пропорционален прошедшему без дифракции опорному пучку
исходной поляризации. Член  как и в скалярной теории голографической записи, вызван двумя факторами: 1)
протяженным характером объекта и 2) игнорированием Брегговских эффектов в голограмме
реальной толщины (или что то же - параксиальным характером нашего рассмотрения).
При z' = ±z0
этот член занимает пространственный интеграл, примерно
вдвое превышающий объект.
как и в скалярной теории голографической записи, вызван двумя факторами: 1)
протяженным характером объекта и 2) игнорированием Брегговских эффектов в голограмме
реальной толщины (или что то же - параксиальным характером нашего рассмотрения).
При z' = ±z0
этот член занимает пространственный интеграл, примерно
вдвое превышающий объект.
Особенно важным является выражение (39'). Здесь 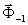 описывает сформированное на расстоянии z' = z0,
изображение исходного объекта c
реконструкцией состояния его поляризации. Аналогично, (40*) описывает действительное
изображение объекта, сформированное симметрично мнимому. Шумовые компоненты
(37'), (38'), как и в скалярной теории голографической записи, могут быть пространственно
отделены от полезного сигнала (39') асимметричным расположением голограммы относительно
опорного пучка в процессе записи /11/.
описывает сформированное на расстоянии z' = z0,
изображение исходного объекта c
реконструкцией состояния его поляризации. Аналогично, (40*) описывает действительное
изображение объекта, сформированное симметрично мнимому. Шумовые компоненты
(37'), (38'), как и в скалярной теории голографической записи, могут быть пространственно
отделены от полезного сигнала (39') асимметричным расположением голограммы относительно
опорного пучка в процессе записи /11/.
В заключение следует отметить, что дальнейшие экспериментальные разработки анизотропно-поляризационного метода голографической записи, по-видимому, должны вестись по пути поисков соответствующих материалов, в том числе обладающих наведенным светом, дихроизмом и оптической активностью,что особенно важно в примене-
нии голографии к фотоупругим исследованиям и переработке оптической информации, а также в оптических исследованиях, где полнота записи и голографической рекострукции существенно важна.
Л и т е р а т у р а
1. М.Борн, Э.Вольф. Основы оптики. "Наука". М., 1970.
2. r .С.jones. josa, 31, 488, 1941.
3. r.c.jones. josa, 32, 486, 1942.
4. r.c.jones. josa, 37, 107, 1947.
5. У.Шерклифф. Поляризованный свет. "Мир". m., 1965.
6. f.kottler. progress in optics. n.h.p.c.a., vol.v1, 331, 1967.
7. a.sommerfeld. optics, acad.press, n.y., 1954.
8. Г.Ван де Хюлст. Рассеяние света малыми частицами. И.Л., М.,1961.
9. d.gabor. proc.roy.soc., a197, 454, 1949.
10. Ю.Н.Денисюк. ДАН СССР, 144, 1275, 1962.
11. e.n.leith, j.upatnieks. josa, 52, 1123, 1962.
12. p.j.van heerden. appl.opt., 2, 393, 1963.
13. Ш.Д.Какичашвили."Оптика и спектроскопия", 33, 324, 1972.
14. Г.В.Скроцкий, Т.Г.Изюмова. Успехи физ.наук, 73, 423, 1961.
15. f.weigert. verhandl. d.phys.ges., 21, 479, 1919.
16. С.В.Чердынцев. ЖФХ, 15, 430, 1941.
17. t.kondo. zs.wiss.phot., 31, 153, 1932.
18. Физический словарь. т.1, ОНТИ НКТП, стр.887. М., 1936.
19. А.Папулис. Теория систем и преобразований в оптике. "Мир", М., 1971.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

