|
|
 |
 |

|
| |
ДИФРАКЦИОННЫЕ СВОЙСТВА ТОЛСТОСЛОЙНЫХ ГОЛОГРАММ
Н.М.Померанцев
Рассматривается явление дифракции света в толстых диэлектрических слоях, имеющих пространственно периодическое распределение показателя преломления. Использование этого явления в голографии приводит к выявлению зависимости интенсивности дифрагировавшего света от пространственной частоты голографируемого предмета. Такая зависимость имеет вид диаграммы направленности толстослойной голограммы и характеризует передачу пространственных частот такими голограммами. Рассмотрены примеры диаграмм направленности.
Задача о дифракции света в толстом слое прозрачного диэлектрика с неоднородным распределением показателя преломления стала актуальной в результате появления толстослойных голограмм. Решение этой задачи дает возможность понять, как происходит процесс восстановления голограмм с толстым слоем. Такой процесс, как известно, имеет свои существенные особенности, отличающие толстослойные голограммы от тонкослойных.
Существует ряд методов решения указанной выше задачи, отражающих те или иные особенности дифракции света в толстом слое. Первое борновское приближение теории возмущений позволяет установить три отличительные черты толстослойных голограмм:
1) избирательность по направлению;
2) цветовую избирательность;
3) гашение второго изображения.
Эти характерные черты установлены на основе анализа фазовых соотношений в дифрагировавших волнах. Однако правильного соотношения амплитуд это приближение дать не может, так как предполагается, что в результате дифракции происходит лишь малое возмущение
исходной волны. В действительности это оовоеи не так. Мы остановимся на одном, достаточно строгом методе, позволяющем получить не только приближенное, но и точное решение уравнений, описывающих дифракцию в толстой слое.
Свет, исходящий от объекта, можно разложить на ряд плоских волн, падающих на голограмму под разными углами (разложение по пространственным частотам объекта). Для выявления дифракционных свойств толстослойной голограммы достаточно рассмотреть одну плоскую волну из всех составляющих и проследить зависимость от угла падения этой волны результата дифракции света на решетке, полученной сложением этой волны с опорной, угол падения которой остается неизменным.
Получившаяся кривая будет показывать, как зависит интенсивность дифрагировавией волны 1-го порядка от пространственной частоты протяженного объекта. Так как плоская волна, соответствующая той или иной пространственной частоте объекта, приходит с определенного направления, то полученную нами кривую можно назвать диаграммой направленности толстослойной голограммы.
В рассматриваемом методе также возможно приближенное решение. При выполнении неравенства α <<cos2Θ, γде α - максимальное относительное изменение показателя преломления и Θ - угол падения опорной волны, можно значительно упростить систему уравнений. В зависимости от величины параметра q=4kd sinΘ tgΘ (k - βолновое число, d - толщина голограммы) эта упрощенная система уравнений будет описывать дифракцию в одной из трех областей:
q <<π/12 - ξ бласть дифракции Рамана-Ната , (1)
π/12<<q<<4π - οπ омежуточная область, (2)
q>> 4π - ξ бласть дифракции Брэгга . (3)
В области дифракции Рамана-Ната интенсивность света в различных порядках дифракции пропорциональна функции Бесселя соответствующего порядка. В этой области существует много порядков дифракции и голограммы с параметрами, удовлетворявшими условию (1), бу-
дут обладать свойствами тонкослойных. Область, описываемая неравенством (2),- переходная между областями Рамана-Ната и Брэгга. Аналитического решения задачи для этой области не получено. В области дифракции Брэгга существуют только два порядка дифракции (нулевой и минус первый). Как показывает решение, для этой области при распространении света внутри среды происходит перекачка энергии из волны нулевого порядка в волну минус первого и обратно. Это обусловлено наличием двух волн с близкими длинами в каждом порядке. Взаимодействие зтих двух волн приводит к "биениям". Из-за этого дифракционная эффективность становится "синусоидальной" функцией толщины голограммы и определяется выражением
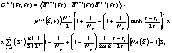 (4) (4)
φ- σ гол падения на голограмму предметной волны, т.е. одной составляющей спектра пространственных частот предмета при записи. Диаграмма направленности толстослойной голограммы имеет один центральный лепесток и целый ряд боковых. Число боковых лепестков увеличивается с увеличением толщины светочувствительного слоя. Одновременно происходит сужение центрального лепестка. Оптимальная передача пространственных частот, т.е. минимальное число боковых лепестков, наблюдается при определенной толщине слоя. Эта толщина определяется из следующего выражения:
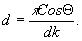 (5) (5)
Точное решение, полученное на основе уравнений Максвелла, имеет вид следующего ряда Фурье-набора плоских волн, распространяющихся в соответствующих порядках дифракции:
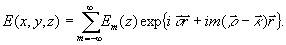
Здесь e m(z)
- комплексная амплитуда волны m-гo порядка, изменяющая свою величину по мере
проникновения света вглубь светочувствительного слоя и поэтому зависящая от
z; 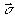 - волновой - волновой
вектор восстанавливающей волны; 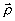 -
волновой вектор опорной волны; -
волновой вектор опорной волны; 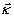 -
волновой вектор предметной волны; -
волновой вектор предметной волны; 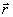 -
вектор с координатами х , у, z. -
вектор с координатами х , у, z.
Для амплитуд Е m(z) получается бесконечная система дифференциальных уравнений. Эта система имеет два интеграла, анализ которых позволяет установить некоторые отличительные свойства дифракции света в толстой слое. Эти два интеграла поедставляют собой два закона сохранения:
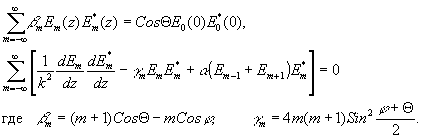
Первый интеграл показывает, что сохраняющейся величиной при дифракции в толстом слое будет поток энергии через поверхность, лежащую в плоскости ХОУ. Три члена второго интеграла можно интерпретировать, соответственно, как кинетическую энергию, потенциальную энергию и энергию связи.
Нетрудно видеть, что γ 0 = γ-1 = 0, величина γm увеличивается с увеличением порядка дифракции и что энергия связи существует только для волн соседних порядков. Отсюда можно сделать вывод, что энергия передается постепенно от волны нулевого порядка к волнам высших порядков, причем потенциальная энергия, увеличивающаяся с увеличением порядка, накапливаетоя в волнах высших порядков и препятствует движению энергий. Интенсивность света уменьшается с увеличением порядка. Максимальная интенсивность света будет для волн нулевого и минус первого порядков.
Решением системы уравнений для функций e m(z) являются почти периодические функции, заданные своими рядами Фурье,
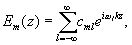
в которых показатели Фурье ω l, определяются с помощью характе-
ристического детерминанта, а коэффициенты Фурье c ml из граничных условий.
Эти величины были рассчитаны с помощью ЦВМ для следующих значений параметров: Θ = 10°; α = 0,01; 0,05; 0,1; 0,2; φ = 10°, 13°, 7°, 4°, 0°. Οπи расчете учтены волны порядков 2, 1, 0, -1,-2 . В спектре собственных частот ωl, для волн порядков 0 и -1 основную роль играют две частоты, в то время как в спектрах для волн других порядков колебания 4-х частот имеют сравнимую друг с другом амплитуду. Решения для α = 0,01. Θ = 10° θ φ = 170 μало отличаются от приближенных. Решения для других значений α θ углов φ имеют существенные отличия от приближенных. Эти отличия обусловлены тем, что для точных решений имеется гораздо больше составляющих в спектре, чем для приближенных. Поэтому вместо "синусоидальных" кривых, изображающих приближенные решения, появляются сложные непериодические кривые. Это хорошо иллюстрирует рисунок. Аналогичная картина наблюдается и для диаграмм направленности, построенных на основе точного решения.
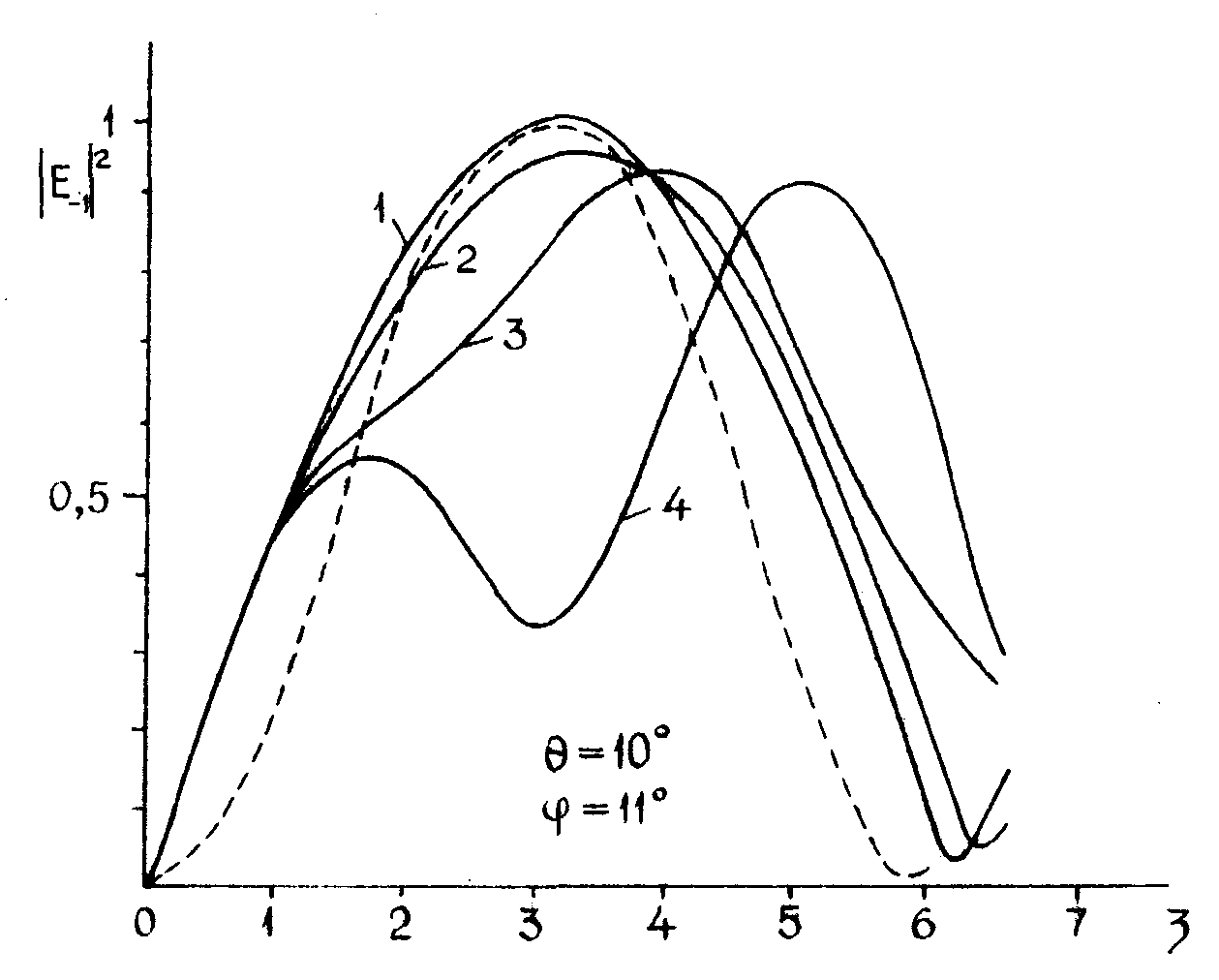
Рис. Сопоставление приближенного и точного решений для Θ = 10°, φ = 11°.
Пунктир - приближенное решение. Для других кривых (точное решение) значения
α следующие: 1 - 0,01; 2 - 0,05; 3 - 0,1; 4 - 0,2. По оси абсцисс отложены
значения величины 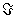 =αkz.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

