methoden zur informationsaufzeichnung
mittels fourierhologramen
werner reichel
veb carl zeiss jena, ddr
z u s a m m e n f a s s u n g.
es werden die mglichkeiten holographlscher aufzeichnungen mit hoher informationsdichte für analoge und digitale signale behandelt, auf praktische verfahren an beispielen eingegangen und die bedeutung der fourierholograimne (f.h.) für filterprozesse diskutiert.
in unserem jahrhundert wird mit gutem recht der information, ihrer speicherung und verarbeitung grosae bedeutung beigemessen, während das vergangene durch die energie gekennzeichnet war.die magnetische aufzeichnungatechnik mit einer miniaturisierten elektronik hat grosse erfolge zuverzeichnen, doch sind gegenwartig ihre grenzen schon abzusehen und diese informationsdichte in der zukunft für schnellen zugriff der daten nicht mehr ausreichend. die optische abbildung hat den vorzug, dass sie sehr bequem durch ein hochwertiges optisches system (objektiv) zweidimensional wirkt; in jeder dimension, im gegensatz zur magnetischen technik gleichberechtigt und gleichzeitig aufgezeichne werden kann.
der extremen verkleinerung wie diese z.b. in der mikrofilmtechnik genutzt wird, sind praktische grenzen gestezt, da staubkorner und beschädigungen wie kratzer einen starken informations -
vrlust herbaifghren können, obvrohl die optik strukturen bis in den m-bereich abzubilden varmag. bei der holographischen technik werden aber die informationen über die gesamte flache integral codiert registriert, so dass eine wesentlich sichere und hohere flaohendichte der konservierung (speicherung) und das auslesen mit grosserer sicherheit erreioht werden kann. hinzu kommen noch die-möglichkeiten der dritten dimension in form der volumenspeioherting, die sehr frühzeitig von denisyuk erkannt wurde, hier aber nicht weiter behandelt werden soll.
wie e.abbe /1/ vor 100 jahren erkannte, lasst sich die optiache abbildung in ewei schritten beschreiben und in der hinteren brennebene entsteht das primäre bild, dessen auflosungsvermogen er durch die numerische apertur beschrieb. wie wir heute wissen, kann dieser prozess duroh die zweimalige. anwendung einer fouriertransformation beschrieben werden. verfolgt man die gedanken, dann erhalt man beim fourierhologramm die grosste speicherdichte, wobei das auflösungsvermögen unabhängigavon der aufzeichnungsmediums ist und nur durch die apertur begrenzt wird /2/. Ähnliche ergebnisse lassen bich auch durch betrachtung der preiheitagrade eines wellenfeldes nach gabor erzielen /3/.
in bild 1 sind die verhältnisse schematisch fur zwei spezialfalle erläutert. die extremfalle ergeben sich durch klassische selirachtungen der linsenformel. der einfachheit sei eine eindinenaionale darstellu ig gewählt und einmal soll die objekt -funktion f(x) vor und hinter-der transformationslinac liegen. o sei eine punktlichtquelle und o' das zugehorige bild und es findet imutr eine fouriertransformation statt. im ersten fall ergibt sich die attplltude in f2 nach g1. (1) und die verallgemeinerte fouriertransformation reduziert sich zu der bekannten bexiehunf der beiden konjugierten brennebenen der linse. im 2. fall verschwindet der quadratiache term und die fouriertransformierte liegt nicht in der brennelene (gl.2). fur den 3, fall, dass das objekt hinter der linse liegt, kann der qua-
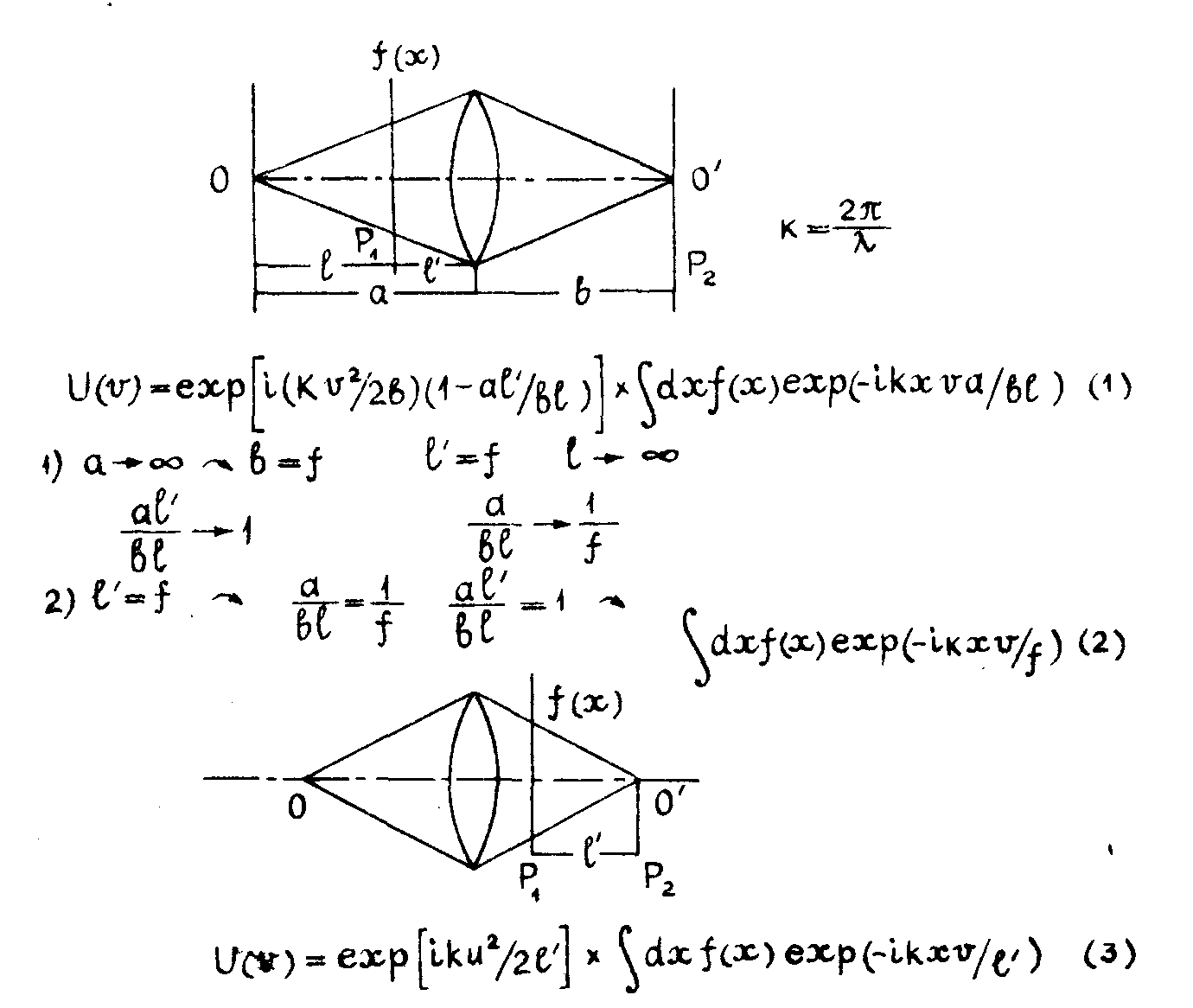
bild 1.
dratische term durch eine punktlichtquelle in p1 ersetzt werden. die amplitude lasat sich dann durch gl.3 beschreiben. dieses prinzip nach stroke /4/ wird in der mikroskopie, mikrofiliatechnik und zur zeichenerkemiung teilweise angendet, dann hier wird eine hohe informationsdichte in eine kleinen flache benotigt. es kann naturlich auch im punkt p1 das hologramm aufgesteilt werden und die rekonstruktionin p2
(x) der referenz -liehtquelle nach gl.6 bestirntt. die grosse des punktbildes wird in allgemeinen grosser durch die abbildungsfehler (spharischc aberration) ale das reine durch beugung begrenzte bild. fur die auflösung gilt dann nach gl.6
r die-einzelnen vergroaserungcn zu berechnen und die grosse der punktlichtquelle zu ermitteln, da das bandbreitenprodukt (space band product) die auflösung bestimmt und wie mc mahon /5/ zeigen konnte, ist z.b. für die mikrofilmtechnik für 1000 linien/mm für eine buchseite-bci 6 facher vergrosserung eine hologranuiigrosse von 1 mm zu erwarten.
eine ähnliche anordnung, in der die hologrammplatte in der hinteren-brennebene einer linse steht und die transparente objekt-funktion und referenelichtquelle in der gleicher ebene liegen, die hinter oder auch vor der linse (bild 2) liegt, jedoch nicht in der vorderen brennebene liegt und mit einen objektwelle beleuchtet wird, ist als quasi-fourier-transfortnations-anordnung bekannt. auch hier gelten die gleichen verhältnisse und wenn man eur linsenlosen anordnung ubargeht, gilt dies noch starker, denn der shpärische phasenfaktor φ(x2) (gl.8) muss mit-der zugenhorigen-referenzwelle der gleiche sein, wie der zugehörigst mit der objektwelle.
eine andere möglichkeit eine unbegrenzte referenzlichtquelle einzusetzen, bieten die fraunhofer hologramme, die ebenfalls mit und ohne linse hergestellt werden konnen. am günstigsten erscheint eint aber die registrierung mit einer ausseraxialen ebenen heferenzwelle mit einer dünnen linse der brennweite p nach bild 3,
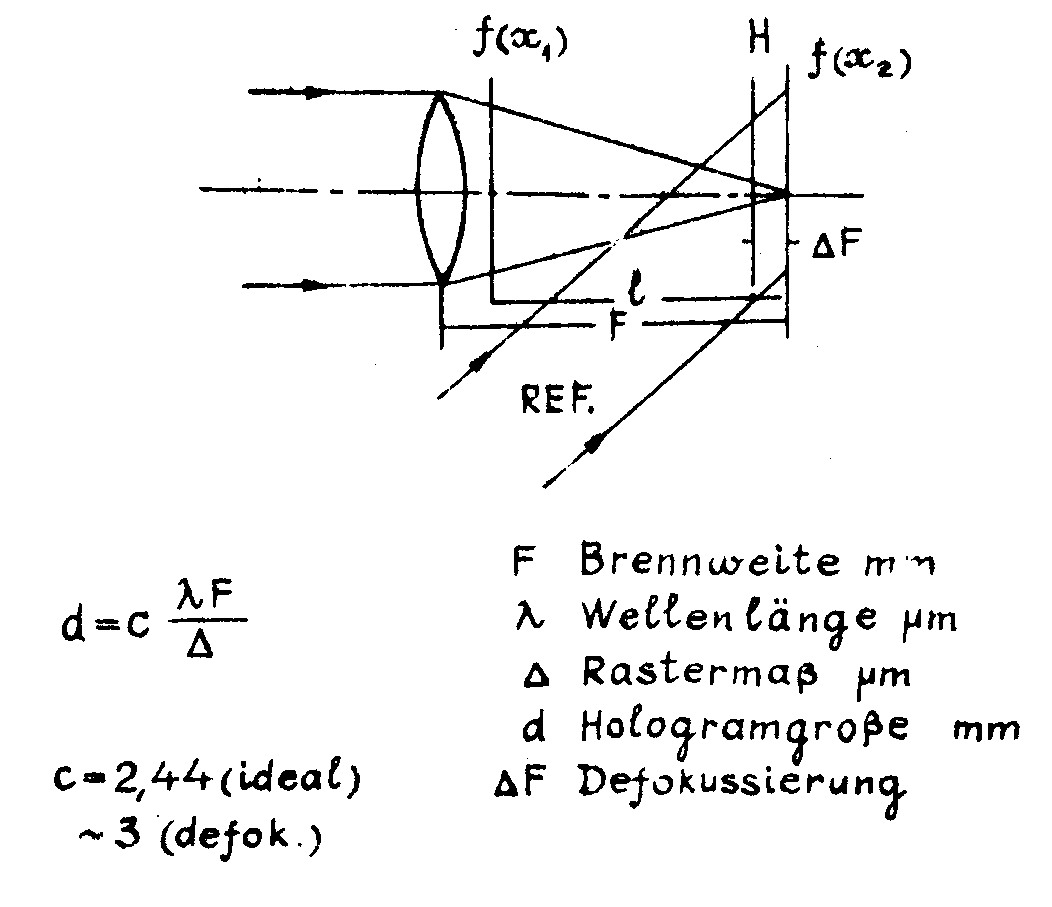
bild 3.
wobeimauuh das objekt mit einer ebenen welle beleuchtet wird, so dass diese beiden hellen in der hiliteren brennebene über die gesamte hologrammebene interferieren. hierzu ist allerdings voraussetzung, dass das optische system gut korrigiert ist. wählt man die objektfunktion f(x1) so, dass diese durch hüll ausserhalb des objektes geht, so können die grenzen im integral auf ±∞ ausgedehnt werden und man erhält, abgesehen von einem konatanten faktor für die aniplitudenterteilung der hologrammebene von objekt näherungsweise eine fourier-transfonnation.unter dieser bedingung spricht man dann auch vom fourier-hologramme, allerdings muss die reierenzwelle eben sein. mit anderen worten müssen die bedingungen des fernfeldus fur die beugung eingehalten werden. besteht z.b. das objekt aus einem punkt, so lässt sich sehr schon die auflosun ableiten, die nur vom winkel-zwischen objekt- and referenestrahl abhängt. die lineenlosen fraunholer-hologramme werden oft als in-une-technik zum nachweis von kleinen partikeln benutzt und sind nich thompson eigentlich mit die ersten holographischen techniken /6/ gewssen.
welche praktischen ergebnisse erreicht werden, soll nun beschrieben werden. will man z.b. digitale uatenraengen, die man in blocke (matrizenanordnung) zusammenfasst, holographisch registrieren, so haben wir 128 x 128 musterpunkte in ein holograiara von ca. 1 nun auf lp2-platten von orwo wolfen gespeichert. die rekonstruktionen sind z.b. aus bild 4 zu erkennen, wobei die blocke nochmals in unterblscke auaaininengefasst sind. diese untertcl lung ist durch empfangeranordnung und technologie bedingt, doch lassen sich diese unterteilungen bei grosseren gitterkonstanten (rastei-mass) zugunsten einer grosseren bichte im hologramm vermeiden, wenn man diskrete bauelemente aneinanderreiht. im vorliegenden beispiel betrug das rastermaas (abstand von bit zu bit) 200 h/m. das signal-rausch-verhältnis betrug mindestens 60, so dass eine elektronische verarbeitung möglich ist. die hologramme wurden zunächst als amplitudenholograr
3) und dadurch die üeugungsrnaxima verschmiert. hierauf hat besonders auch mikaeliar /7/ nach la macchia /8/ hingewiessen und diese Überlegungen wurden durch rechnungen von lang /9/ gestutzt. eine befokussierung hat aber auch nachteile, da man gunakig so defokussiert, dass das 1. nebenmaxinoini noch mit erfasst wird, so daes das auflssungsvemogen vom theoretischen faktor nach bild 3 von 2.44 auf nahezu-3 vermindert wird und ausserdem es oft ungünstig ist, aueserhalb der brennebene die hologramme zu registrieren. es ist deshalb von burckhardt /10/ der vorschlag einer statistischen phasemnaske dicht hinter der datenmaske gemacht wordtn, der auch noch günstigere signal-fiausch-verhaltnisse ergibt. hier wird im einfachsten falle eine statistische verteilung der daten mit den phase 0 und 180° gewählt. im bild 5 erkennt man eine solche statistik, wobei die hellen felder etwa die phase 0° und die dunklen felder die pliase 180° bedeuten mogen und die statistisch gleich verteilt sind. während man bei befokusflierung mehr oder weniger unscharle gitterstrukturen im beugungsbild erhalt, so bildet eich bei der verwendung einer phasemaske eine statistik innerhalb des airy-scheibchens aus (bild 6). da im vorliegenden. pall die phasenmaske aus 4 quadranten zusammengesetzt wurde, sind noch schwache symmetrien in der 1.ordnung beobachtet worden, doch lässt sich durch eine vollständige statische verteilung über die gesamte flache diese vollständig beseitigen. in bild 4 wurde eine dichtevoll 1,6*104 erreicht, doch lasst sich diese durch wegfall der zwischenräurae und auf 0,8 mm-hologranimgrosse noch steigern, so dass man-zwischen 104 - 105 / mm2 erreichen kann. bei verwendung von einer beschriebenen zweistufigen phasehmaske gibt goldmann /10/ ein signal-untergnmd-rauschverhaltnis von wenigstens 10:1 an, welches such von uns bestätigt werden konnte. gebt man nun zu mehrstufigen statischen fasenschritten über, so steigt zwar der technische aufwand, doch wird man von der konfiguration der eingangesignale innerhalb der matrix durch berechnung der wahr -

bild 5.

bild 6.
schenlichkeitsverteilung weitgehend unabhängig, da wie takeda /11/ mit einer 4 stufigen phasenmaske zeigte, dessen aufwand noch tragbar ist, kann diese forderung erfullt werden. es ist natürlich auch inoglich die eingangaeignale; sobald diese in eine ahnlich bzw. gleiche anordnung wie die statistische phasen-verteilyng kommen, durch elektronische mittel umzocodieren, da ja die eingangesignale in der kehrzahl ohnediuci in form elekt -rischer signale vorgegeben sind und in optische signale transformiert werden roussen. ein weiterer vorteil der mehrstufigen phaseninaske ist auch die günstigere beugungseffektivität. Über die tiloglichkeiten einer einfachen herstellung und der erforderlichen genauigkeiten wird 3.2. bei uns gearbeitet. in diesem zusammenhang sei erwähnt, dass die transformation elektrischer signale in optische durch die matrixanordnung z.b. bei verwendung von flüssigen kristallen, die die dynamische streuung benutzen, verschlechterung der kohärenzeigenschaften zur folge hat. in bild 7 ist eine solche anordnung zu sehen und die geschalteten muster sollen guten kontrast zeigen, der durch hohe spannungen bedingt; die kohärenz f. die hologrammaufzeichnung kann zwar wie unten gezeigt, einiges ausgleichen, doch ist es günstiger, den elektro-optischen effekt durch doppelbrechung hier-für auszunutzen oder andere effekte in verbindung mit transparenten keramiken.
ein weiteres eehr wichtiges praktisches problem zur durchführung der fourier-transformation liegt bei den verwendeten optiken. wie bereits eingangs erwähnt, spielen die aberrationeil für die abbildung eine rolle,wenn man zu ausgedehnten bildfeldern und grosaem Öffnungsverhaltnie übergeht. um die hohe speicherdichte auszunuteen, wird man zwectonassig für archivspeicher u.a.grosse informationsmengen viele soleher hologramme nach kumle dicht aneinander setzen und über echnelle lichtablenker positionieren und auslosen. bild 8, zeigt eine solche prinzipielle anordnung. in diesem falle wird die optik auch ausseraxial beansprucht und versuche mit konventionellen optiken haben gezeigt, dass diese nicht den anförderungen entsprechen. in bild 9 haben wir versuchsobjektive 3,5/150 gegeneinandergesetzt und

bild 7.
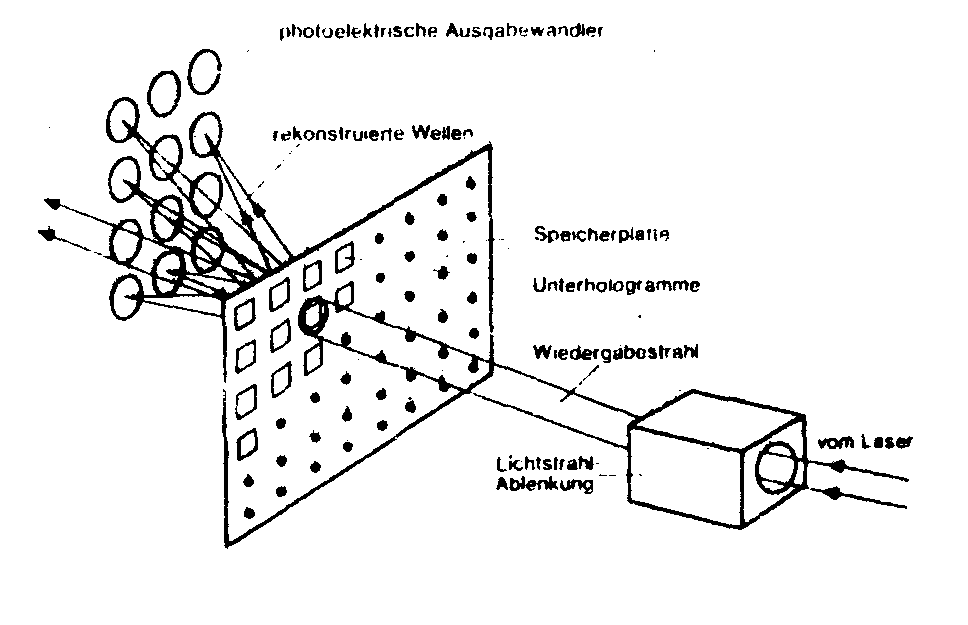
bild 8.

bild 9.
einmal axial mid in bild 10 um 15° bildwinkel yeschwenkt, eine datenvorlage aufgenommen. aus bild 10 erkennt man die verzeichnung, die besonders korrigiert werden f kann dadurch erheblieh vermindertwerden muss. in vorliegenden fall wurde die verzeichnung durch einen kunstgriff zur besseren demone-tration vergrosaert. eine solche fourier-transfonnationsoptik iet deshalb zweckmässig aus zwei symetrischen hälften aufgebaut. sine bildtransformation muss deahalb zur abbildung in die ebene x2 nach bild 3 spianatisch und anastigciatisch erfolgen und der haupstrahl muss die sinusbedingung erfullen. solche systeme rait geringer Öffnung und kleinem bildwinkel sind von h.h.hopkins und mitarbeitern angegeber /12/ und neuerdings auch von von bieren /13/ aufgegriffen worden. die korrektion solcher systeme ist an den holographischen aufbau bezugl. referenssstrahlfuhrung und andere geometrisch-optische forderungen gebunden. tatsache ist jedoch, daea für die anwendung im nicht paraxialen gebiet, be sondere systeme verwendet werden mussen und fotoobjektive wenig geeignet sind.
da die filtertechnik in zueataiiienfasaonden darstellungsn disser schule von vienot und lanal ausfuhrlich behandelt wurde, sei nur herausgegriffen, dass man durch verachriften für das schriftbild und trennung sowie klassifizierung der symmetrieeigenscgaften für lineare und radiale elemente z.b. von show /14/ einige fortsehritte zu verzeichnen hat.
auch die parallelverarbeitung nach kock /15/ und die code-trans-formationetechnik, indem man 9 oder 16 bits in kombination nach nakajima /16/ verwendet, ist zwar aufwendig, aber für einen analog-wandler aussichtsreich als holotablett zur erkennung von handgeschriebenen daten als eingabegerat für computer entwickelt worden. schliesslich seien nicht unerwähnt, die arbeiten von soroko /17/ u.mitarbeitern über die neuen-moglichkeiten eines optischen beugungsgitters init purchensprungea zur zeichenarkennung. vienot /18/ hat durch seine unterauchiingen der charakterischen spektralen frequenzbereiche und bander dazu beigetrasen, dass die filter besser angepasst werdea konnen.
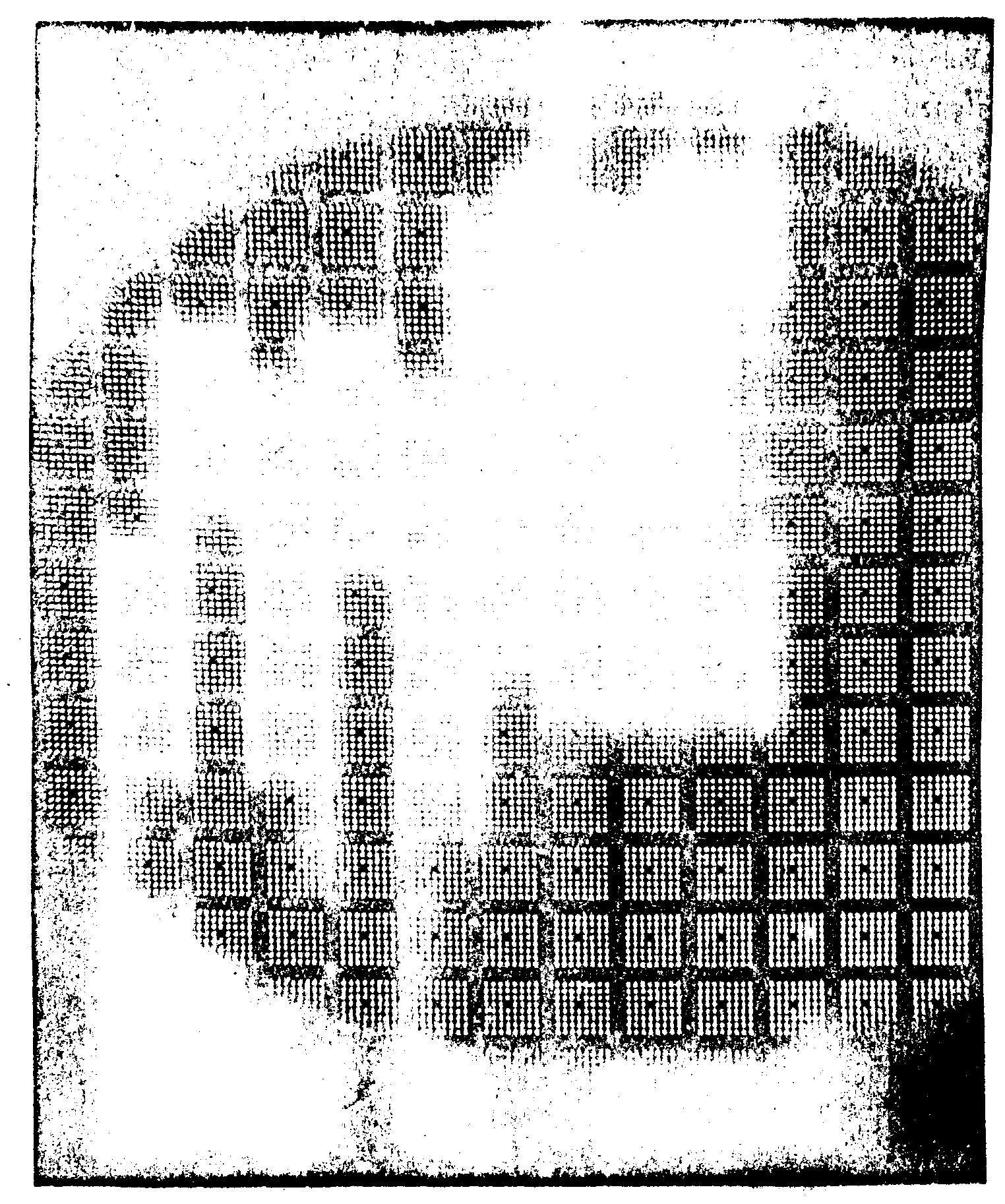
bild 10.
auch die auswertung von versuchsreinen mikroskopischer aufnahmen oder photograimmetrischer luftbilder konnten solchemethoden in zukunft revolutieren.
zum abschluas mochte ich für die gezeigten experimentellen beispiele den mitarbeitern dipl.-phys. woirgang freitag, elfi klitzsch und udo shafer danken.
r e f e r e n c e s
1. e.abbe. beitrage zur theorie des mikroskopen und der mikroskopischen wahrnehmung, archiv für mikroskopisches anatomie von max schultze, 9, s.413-468, 1873.
e.abbe. gesammelte abhandlungen, bd. 1 s. 45-100, 1904.
2. f.i.diamond. magnification and resolution in wavefront reconstruction, j.opt.soc.am., 57, 4s, 503-8, 1967.
3. j.t.winthrop. struxtural-information storage in holograms, ibm. j. res.develop., 14, 5 s. 501-8, 1970.
4. g.w.stroke, d.brumm, a.funkhouser. three-dimeneional holography with lensless fourier-transform holograms and coarse p/n polaroid film, j.opt.soc.amer., 55, 10 s. 1327-28, 1965.
5. d.h.mc mahon. magnification abarrations in fourier-transform optical data storage, j.opt.soc.am., 61, 7 s. 915-23, 1971.
6. b.j.thompson. application of hologram teohniquea for particle-size analysis, appl.optics, 6, 3 s. 519-26, 1967.
7. a.l.mitikaeliane, v.i.bobrinev. holographie memory devices, opto-electronics, 2, 4 s. 193-99, 1970.
8. j.t.la macchia. formation and evaluation of hologram array for optical memory, j.opt.soc.am., 59, 4 s, 490,1969.
9. m.lang, g.goldmann, p.graf. a contribution to the comparifcon of single exposure and multiple exposure storage, appl.optics, 10, 1 s. 168-73, 1971.
10. g.goldmann. holographis storage of digital data maske. optik, 34, 3 s. 312-20, 1971.
11. y.takeda. hologram memory of high quality and high information storage density, jap.j.appl.physics, 11, 5 s. 656-65, 1972.
12. b.a.f.blanford. a new syetem for use in optical data-processing, proc.optical instrumenta and teohniques, reading 1969, oriel press, s. 435-43, 1970.
13. k.von bieren. lens design for optical fourier transform systems, appl.optics, 10, 12 s. 2739-42, 1971.
14. y.sliow. optical character recocnition using a new method or characteristic extraction. appl.optics, 11, 5 s. 1271-73, 1972.
15. m.kock, g.rabe. parallel and time sequential optical multiplex systems for pattern recognition, opt. comm., 5, 2 s. 73-77, 1972.
16. m.nakajima, t.morikawa, k.saurai. automatic character reading using a holographic data processing technique, appl.optics, 11, 2 s. 362-67, 1972.
17. l.m.soroko. computer simulation of the discrete analog of the diffraction grating with ruling jump, comm. joint inst. nuclear res., dubna, p13-6607, 1972.
18. j.c.vienot, j.duvernoy, g.tribillon, j.-l.tribillon. coherent optics, holography and information, brighton 1972, proc.electro-optics international, 2, s.99-116, 1972.

