ГОЛОГРАММНАЯ ОПТИКА И ПЕРСПЕКТИВЫ ЕЕ ПРИМЕНЕНИЯ
К.С.Мустафин
Рассматриваются изображающие свойства и аберрации плоских и неплоских голограмм. Показана возможность уменьшения сферической аберрации и комы путем подбора кривизны поверхности голограммы. Исследована возможность повышения разрешающей способности голограммной оптики путем использования высших порядков дифракции. Рассматриваются фильтрующие свойства трехмерных и двухмерных голограмм и допустимые деформации поверхности голограммной оптики.
Под термином "голограммная оптика" понимаются голограммы, применяемые в качестве оптических элементов (корректирующих, фокусирующих, отклоняющих, диспергирующих, фильтрующих и т.п.). Примерами практического применения голограммной оптики являются голограммные дифракционные решетки /1/, голограммы системы точечных источников для мультиплицирования изображения /2/ и др.
В настоящее время, однако, голограммы еще не могут успешно конкурировать с обычными оптическими элементами ввиду их относительно низкой дифракционной эффективности и необходимости использования монохроматического источника света. Но в ряде случаев голограммные оптические элементы обладают несомненными преимуществами или являются незаменимыми, например, при решении задач коррекции аберраций
специальных оптических систем, при контроле сложных оптических поверхностей и др.
Достоинством голограммной оптики является также малый вес, дешевизна и простота их изготовления, что особенно важно при конструировании и изготовлении крупногабаритной оптики
.
Отмеченная выше сравнительно низкая дифракционная эффективность гогограмм, ограничивающая широкое применение их в качестве
оптических элементов, не является принципиальным недостатком. Работы, проводимые по поиску путей повышения эффективности голограмм, дают положительные результаты. По данным /3/ дифракционную эффективность голограмм, записанных на галоидо-серебряных слоях, можно повысить до 70%.
Для широкого применения голограмм в качестве оптических элементов необходимо разработать такие оптимальные методы расчета и изготовления их, подобно тому, как это уже сделано для обычной оптики. В литературе имеется ряд работ, посвященных исследованию изображающих свойств и аберраций голограмм, а также анализу возможности конструирования оптимальных систем с
использованием голограммных оптических элементов /4-10/. Их Можно принять за основу при расчета и изготовлении голограммных оптических элементов с заданными характеристиками.
Таким образом, есть все основания полагать, что голограммная оптика в ближайшее время найдет широкое практическое применение.
В данной статье рассматриваются некоторые частные вопросы, относящиеся к использованию голограмы в качестве оптических элементов: изображающие свойства и аберрации неплоских голограмм, возможность использования высших порядков дифракции, допустимые деформации поверхности и фильтрующие свойства голограммных оптических элементов.
i.
Изображающие свойства и аберрации неплоских голограмм
Изображающие свойства и аберрации плоских голограмм рассмотрены и исследованы в ряде работ /4-7,11/ Однако на практике могут встречаться такве и случаи неплоских голограмм, например, при изготовлении голограммных оптических элементов: дифракционных решеток, линз и т.п. Поэтому представляется целесообразным рассмотреть изображающие свойства и аберрации голограмм, записанных на тонком светочувствительном слое, имеющем форму сферы (сферические голограммы).
Предположим, что голограмма записывается на светочувствительном слое, нанесенном на сферическую подложку с радиусом кривизны Р. Введем декартову систему координат (х, у, z), начало ко-
торой лежит на поверхности сферы и совпадает с центром голограммы, а ось z проходит через центр сферы.
Рассмотрим случай записи и реконструкции голограммы с использованием точечных источников. Полагая, что суммарное значение фазы интерферирующих (при записи голограммы) и восстанавливающих волн в каждой точке голограммы равно нулю в каждой данный момент времени, в первом приближении можно получить следующие соотношения /12/:
 (1)
(1)
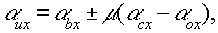 (2)
(2)
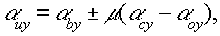 (3)
(3)
где
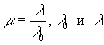 - длины волн света при голографировании и восстановлении, соответственно;
ri - расстояние от точечного
источника света до центра (вершины) голограммы; αix
- длины волн света при голографировании и восстановлении, соответственно;
ri - расстояние от точечного
источника света до центра (вершины) голограммы; αix,
αiy,
αiz
- направляющие косинусы вектора 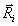 ,
направление которого совпадает с направлением распространения фронта световой
волны; значки i = u, b,
с , о относятся к восстановленной, восстанавливающей, объектной и опорной волнам,
соответственно; верхний
знак относится к минимуму, а нижний - к действительному изображениям. Отметим
здесь правила знаков для ri
и ρ: ri>0
для расходящейся волны и ri<
0 для сходящейся волны; ρ
> 0 , κогда центр сферы находится
на положительной полуоси z,
и ρ < 0
, когда центр сферы находится на орицательной полуоси z.
,
направление которого совпадает с направлением распространения фронта световой
волны; значки i = u, b,
с , о относятся к восстановленной, восстанавливающей, объектной и опорной волнам,
соответственно; верхний
знак относится к минимуму, а нижний - к действительному изображениям. Отметим
здесь правила знаков для ri
и ρ: ri>0
для расходящейся волны и ri<
0 для сходящейся волны; ρ
> 0 , κогда центр сферы находится
на положительной полуоси z,
и ρ < 0
, когда центр сферы находится на орицательной полуоси z.
Уравнение (
1) связывает расстояния, а (2) и (3) определяют угловые соотношения между точечными источниками при голографировании и восстановлении.
Из (
1) видно, что фокусирующие свойства сферических голограмм зависят от кривизны поверхности. Как и следовало ожидать, при ρ→∞ уравнение (1) совпадает с соответствующим выражением для плоской голограммы /11/. Уравнения (2) и (5) не отличаются от случая плоской голограммы.
Волновые аберрации 3-го порядка для сферических голограмм имеют вид;
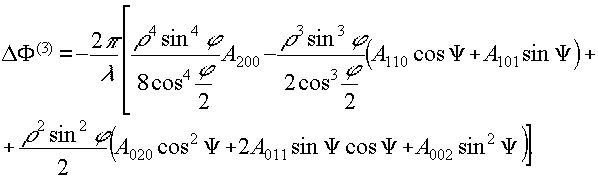 (4)
(4)
Здесь ρ
, φ, ψ - ρферические координаты рассматриваемой точки на голограмме (начало координат в центре сферы радиуса ρ); коэффициенты А200 - сферическая аберрация, А110 и А101 -
комы и А020, А001 и А002 - астигматизма. Последние могут быть представлены в виде:
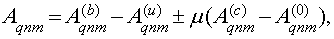 (5)
(5)
где
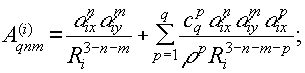
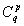
- биноминальные коэффициенты, i = u, b, c, o.
Из (5) следует, что коэффициенты сферической аберрации и комы зависят от от ρ, а коэффициенты астигматизма совпадают со случаем плоской голограммы.
Зависимость коэффициентов аберрации от
ρ μожно использовать для уменьшения сферической аберрации и комы, обусловленных изменением длины волны при восстановлении. Анализ показывает,что, например, для случая одноосевой голограммы точечного источника, записанной с использованием плоской опорной волны, сферическую аберрацию и кому можно существенно (на порядки величины) уменьшить по сравнению со случаем плоской голограммы в широком интервале длин волн при выполнении условия
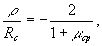
где
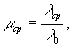 λср
λср - средняя длина
волны рассматриваемого интервала длин волн.
Приведенные выше формулы будут полезны при расчете и конструировании голограммных оптических элементов и систем.
2.
Анаморфотные свойства голограммных оптических элементов
При использовании голограмм в качестве оптических элементов следует иметь в виду, что в отличие от одноосевых голограмм двуосевые голограммы могут обладать свойствами анаморфотной оптики, т.е. разным угловым увеличением в двух взаимно-перпендикулярных плоскостях. Это следует из соотношений (2) и (3).
В самом деле, рассмотрим два случая.
а) Пусть αсу=αоу=αсх=αох=0 что соответствует одноосевому случаю голографирования при нормальном падении света на фотопластинку. Согласно (2) и (3), для угловых увеличении Мxz и myz такого оптического элемента в двух взаимно-перпендикулярных плоскостях (xz) и (yz) можно написать:
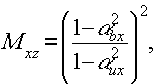
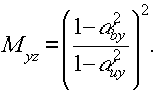
Так как в рассматриваемом случае, согласно (2) и (3),
αbx=αux, αby=αuy тo Мxz = Мyz = 1.
Следовательно, одноосевые голограммы имеют одинаковое увеличение во взаимио-перпендикулярных плоскостях и не обладают свойствами анаморфотной оптики.
б) Пусть
αcy=αoy=0,
но αcx ≠ αox, что соответствует двухосевой голограмме с углом голографирования, лежащим в плоскости xz. Для этого случая из (2) и (3) имеем:
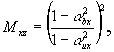
и myz = 1
Так как в общем случае
αbx ≠ αux,
но Мxz ≠ m
yz в, следовательно, двухосевые голограммы обладает свойствами анаморфотной оптики.
Различие в угловом уввличеяим двухосевых голограмм во взаимно-перпендикулярных плоскостях может быть сведено до минимума
только вблизи угла восстановления, удовлетворяющего условию
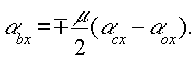
На рис.1 приведено изображение участка миры №5, полученное с помощью двухосевого голограммного фокусирующего элемента при следующих уоловиях: α
cx=
αcy=
αoy=0
, αox=0,755;
плоская опорная волна; λ0 = 632,8 нм. Изображение получалось при αbx=
0,755 и λ=λ0. Из рис.1 видно заметное искажение изображения, обусловленное анаморфотным свойством двухосевой голограммы. Измерения показывают, что величины искажений согласуются с расчетными данными.

Рис.1. Изображение участка миры №5, полученное с помощью двухосевого голограммного фокусирующего элемента.
Таким образом, двухосевая голограмма как оптический елемент, эквивалентный линзе, может вносить значительные искажения в формулируемое изображение, и это обстоятельство необходимо учитывать при конструировании голограммных оптических элементов. В одних случаях анаморфотные свойства голограммной оптики могут вайти полезное применение (например, в кинематографии), а в других случаях они окажутся нежелательными. В частности, различные схемы голографических мультипликаторов изображений с использованием двухосевых голограмм, предложенные в ряде работ (см., например /2/), должны применяться на практике с большой осторожностью ввиду неизбежных искажений, получаемых при этом изображении. В то же время одноосевые голограммы свободны от указанного недостатка и более подходят для этой цели /2/.
3.
Использование высших порядков дифракции
С точки зрения перспектив применения голограммной оптики представляет интерес исследовать отображающие свойства голограмм в высших порядках дифракции /13,14/. Как будет показано ниже, использование высших порядков дифракции голограмм, применяемых в качестве оптических элементов для формирования изображений, позволяет достичь, по крайней мере, вблизи оптической оси голограммы, более высокого разрешения, чем разрешение оптики, использованной при получении самих голограмм.
При использовании высших порядков дифракции соотношения (1), (2), (3) и (4)
остаются в силе, если принять
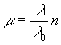 ,
где n - порядок
дифракции.
,
где n - порядок
дифракции.
Для упрощения задачи рассмотрим частный случай одноосевой плоской голограммы
точечного источника при плоской опорной волне. Если такую голограмму осветить
плоской волной при λ
=λ0,
то в n-ом порядке
дифракции на расстоянии фокуса 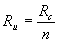 образуется пятно рассеяния с диаметром
образуется пятно рассеяния с диаметром
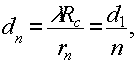 (6)
(6)
где
r- радиус голограммы; d1 - диаметр пятна рассеяния в изображении, восстановленном в первом порядке дифракции.
Так видно из (6), используя высшие порядки дифракции, можно восстановить изображение точки с меньшим диаметром пятна рассеяния, чем при получении самой голограммы. Это значит, что линейное разрешение голограммной линзы можно увеличить путем использования высших порядков дифракции.
Следует отметить, что в общем случае применение высших порядков дифракции для увеличения линейного разрешения голограммной линзы имеет ограничение, обусловленное возрастанием роли сферической аберрации с ростом порядка дифракции
n. Однако этого ограничения не будет, если выполнено условие λ=λ0/n,
т.е. μ=1 при всех n. Важно подчеркнуть, что в последнем случае имеется выигрыш в n раз как в линейном, так и в угловом разрешении. Отсюда следует, что голограмнная оптика, изготовленная с исполь-
зованием длины волны λ
0 в видимой области спектра, может быть применена для получения безаберрационных изображений в вакуумной ультрафиолетовой области спектра с длиной волны λ=λ0/n.
Для экспериментальной проверки приведенных выше выводов были изготовлены две одноосевые голограммы точечного источника с применением плоской опорной волны. Голограммы регистрировались на фотопластинках типа
kodak -649 f с использованием гелий-неонового лазера. Фокусные расстояния rс голограмм были 224 мм и 24,5 мм соответственно. Параметры второй голограммы выбраны такими, что, согласно расчетам, использование высших порядков дифракции не должно привести к выигрышу в разрешении ввиду заметного вклада сферической аберрации.
Предельное разрешение обеих голограммных линз в различных порядках дифракции n = 1, 2, 3, 4 определялось по формируемым ими в соответствуюядах порядках дифракции изображениям миры.
На рис.2а,б приведены кривые зависимости предельного разрешения голограмм от фокусного расстояния, рассчитанные с учетом вклада сферической аберрации. Там же приведены экспериментальные данные, полученные с помощью упомянутых выше голограмм для n = 1, 2, 3, 4. Как видно из рис.2а,б имеется удовлетворительное согласие между теорией и экспериментом.
4.
Фильтрующие свойства голограмм
Известно, что объемные голограммы, записанные во встречных пучках по методу Денисюка Ю.Н.,обладают свойством спектральной селекции к могут быть использованы в качестве светофильтров. Полуширина Δλ ρпектрального пропускания таких голограмм определяется их эффективной толщиной l:
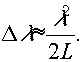
между тем двумерная голограмма точечного источника также может использоваться в качестве светофильтра, если в фокусе поместить диафрагму малого размера. Полуширина Δ
λ ςакого фильтра будет определяться отношением диаметра σ диафрагмы к диаметру d голограммы Δλ=λ σ/d.
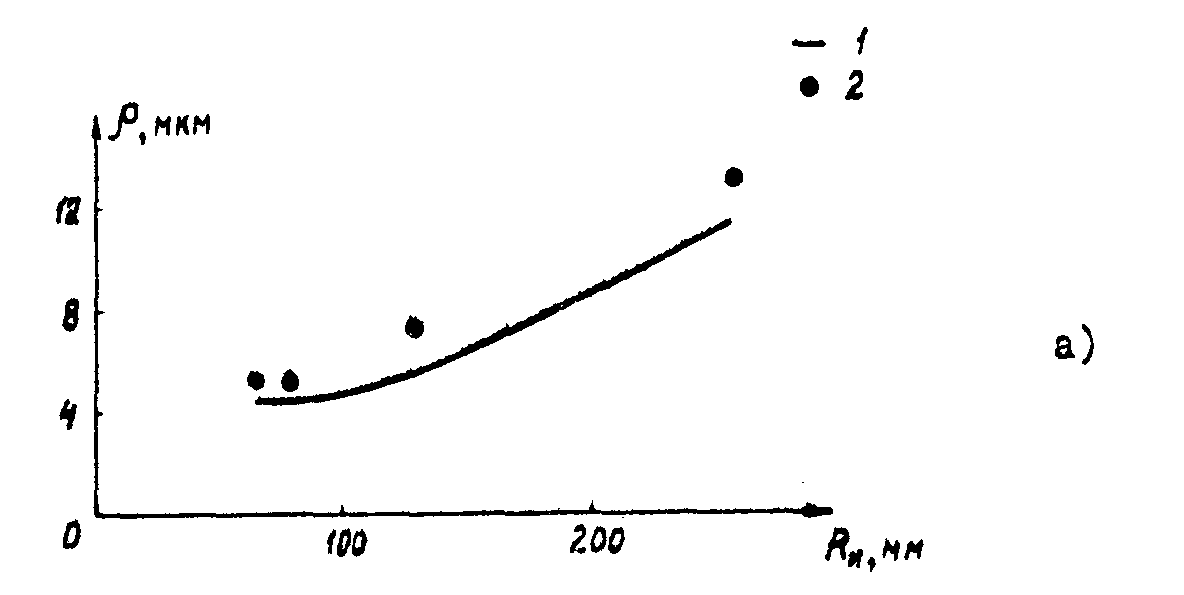
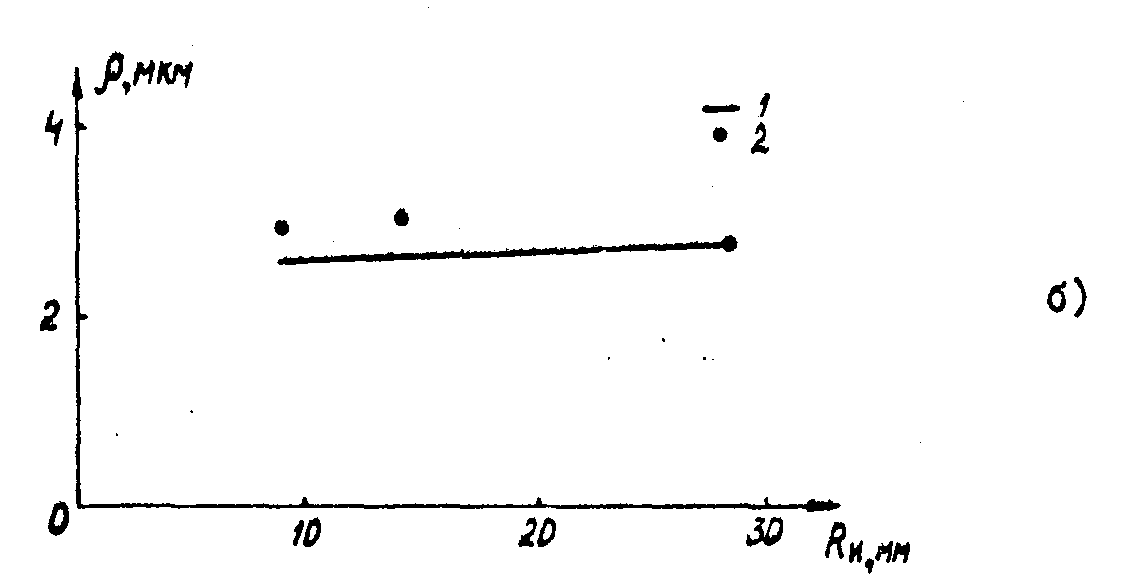
Рис.2. Кривые зависимости предельного разревения голограмм ρ
n от фокусного расстояния ru. 1 - теория; 2 - эксперимент; а - для голограммы с rc = 224 мм; б - для голограммы с rc = 24,5 мм.
Например, при σ = 0,1 мм,
d = 25 мм и λ = 500 нм Δλ = 2 νм. Фильтры на таком принципе могут быть выполнены и для одновременной фильтрации нескольких избранных длин волн. Голограммные линзы могут найти применение также при разработке фокальных монохроматоров.
5.
Допустимые деформации поверхности голограммнрй оптики
С точки зрения технологии изготовления и правильного использования голограамной оптики представляет интерес оценка допустимых деформаций их поверхности. Анализ показывает, что допустимые деформации поверхности голограммной оптики зависят от требуемого разрешения и условий их использования. Для простоты снова ограничимся рассмотрением одноосевой голограммы точечного источника как эквивалента линзы. Если такая голограмма используется в отраженном свете, то из условия Релея непосредственно следует, что деформации Δz поверхности гологракммы в направлении нормали не должны превышать Δz
λ/8 где λ - длина волны света. В проходящем свете, однако, допустимы значительно большие деформации. Например, при достаточно тонкой подложке в проходящем свете допустимы деформации Δz
d2/8, где d - минимальный период разрежаемой структура в изображении. Отсюда следует, в принципе, возможность изготовления и использования легких складывающихся крупногабаритных голограммных оптических элементов.
Для иллюстрации на рис.3а,б приведены снимки изображений миры №5, полученные с помощью одной и той же голограммы точечного источника, записанной на гибкой подложке. Поверхность голограммной линзы имела заметные изгибы, поэтому в отраженном свете формируется сильно искаженное изображение (рис.3а), тогда как в проходящем свете изображение удовлетворительное (рис.3б).
В заключение следует подчеркнуть важность проблемы повышения дифракционной эффективностм голограмм для успешного их применения в качестве оптических элементов, а также разработки методов изготовления голограмм с концентрацией энергии в заданном порядке дифракции.

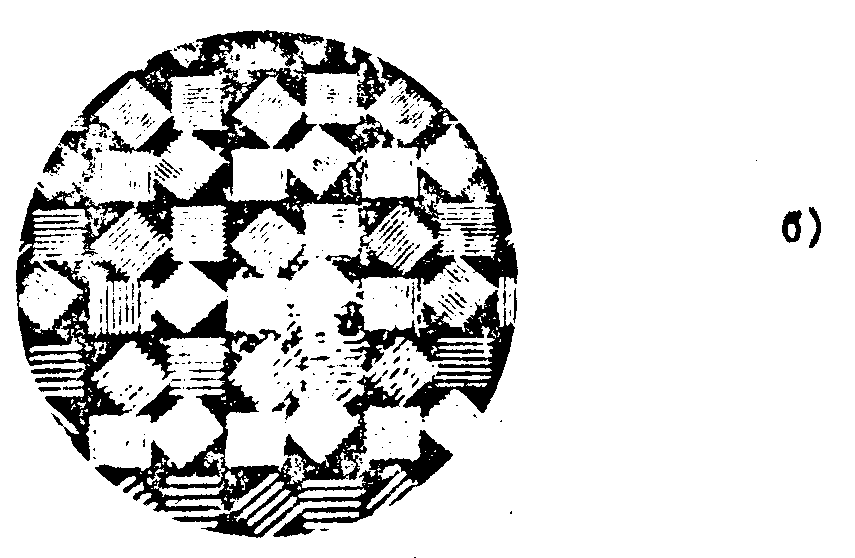
Рис.3. Изображеняя миры №5, пояучвиные о помощью одноосевого голограммного фокусирующего элемента, имеющего заметные изгибы поверхности.
а - в отраженном свете;
б - в проходящем свете.
Л и т е р а т у р а
1. jobin tvon, difraction gratings. arcueil france, 1969.
2. Г.Н.Буйнов, К.С.Мустафин. Исследование возможности применения одноосевых голограмм для мультиплицирования изображений. Оптика и спектроскопия, т.34, вып.5, 1973.
3. А.Л.Микаэлян, В.И.Бобринев, К.С.Богомолов, Л.П.Вахтанова, В.К.Козлова, С.М.Малинин. О возможности использования фазовых голограмм для создания оптических элементов. В сб. "Квантовая электроника", № 6, М., "Советское радио", 1971.
4. e.k.leith, j.upatnieks, k.a.hains. microscopy by wavefront reconstruction. josa, 55, 8, 1965.
5. r.w.mater. magnification and third- order aberration in holography. josa, 55, 8, 1965.
6. e.b.champaghe. nonparaxial imaging, magnification, and aberration properties in holography. josa, 57, 1, 1967.
7. j.f.mills. imaging and magnification properties in holography. opt.acta, 19, 3, 1972.
8. j.n.latta. computer-based analysis of hologran Imagery and aberrations. appl.optics, 10, 3, 1971.
9. i.h.latta. computer-based analysis of holography using ray tracing. appl.optics, 10, 12, 1971.
10. i.h.latta.
Аnаlуsis of multiple hologram optical elements with low dispersion and low aberrations. appl.optics, 11, 8, 1972.
11. Г.Н.Буйнов, Р.К.Гизатуллин. К.С.Мустафин. Исследование влияния аберраций голограмы на качество изображения."Оптика и спектроскопия", т.3
4, вып.4, 1973.
12. К.С.Мустафин. Аберрация тонких голограмм, изготовлевных на сферической подложке. "Оптика и спектроскопия", т.35, вып.6, 1973.
13. r.pawluczyk. holographic imaging of a point object in hiener diffraction orders. optica acta, 19, 4, 1972.
14.
Г.h.Буйнов, А.Е.Лукин, К.С.Мустафин. Об использовании нелинейных эффектов голограмы, примеияеиых в качестве оптических элементов. Оптическая голография, Ленинградский дом научно-техняческой пропаганды, Л., 1972.

