problems of coherent light spekle in holographic Imagery
w.t.welford
imperial college, london, great britain
coherent light speckle, or laser speckle as it is usually called, sets a limit to resolution when the speckle is intrinsic to the object, i.e. when it is caused by roughness on the object which is comparable with or greater than the wavelength of light. although interest in speckle has developed only in the last 10-15 years, the essential theory was given sixty years ago by von laue /1/. we
summarize these properties, which were recomputed by modern techniques by, e.g. dainty /2/.
if a speckle pattern is produced by quasimonochromatic coherent light or by laser light on a rough surface and if the speckle ia viewed either near the surface or at some distance from it an irregular random distribution of intensity is seen, if the mean intensity is <i> the probability density of intensity at a given point is given by
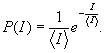 (1)
(1)
the negative exponential probability density, familiar in other fields of physios, has variance <i>1 and the most probable intensity is zero; this accounts for the very high contrast of speckle patterns as seen visually and it shows why they have such a bad effect on optical resolution.
the lateral scale of the speckle pattern depends on the angles between the interesting wavefronts which interfere to tow the pattern; the greater this angle, the smaller will be the scale of the speckle. this lateral scale can best be characterited by the power spectrum or wiener spectrum of intensity fluctuations; it is found
to be the autocorrelation of the square of the aperture function of the optical system used. to take the simplest case, suppoae the speckle is viewed through a system with a circular aperture of semi-angle
α, then the power spectrum intensity fluctuations scanned in any direction is given by
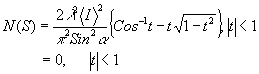 (2)
(2)
where
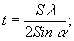 (3)
(3)
in these equations
λ is the wavelength, <i> ia the mean intensity and s is the spatial frequency of the intensity fluctuations. this function is identical in form to the wellknown incoherent optical transfer function for an aberration-free aperture. it can be seen that the speckle always contains detail of size equal to the resolution limit of the detecting system.
in any situation where the detail in the Image approaches the resolution limit intrinsic speckle will be a nuisance. two examples are, bubble chamber holography and holographic microscopy. sometimes it may happen that the hologram can be recorded in such a way as to reduce the effect of speckle but when this is not possible we have to seek ways of minimising the effects in reconstruction. the effects of speckle in images are not like the noise usually encountered in physical detection problems because speckle has very non -gaussian statistics /3/. thus for example if we wish to detect an isolated object such as a bubble in a bubble chamber track the usual method of matched filtering does not give the best results by any reasonable criterion.
several methods have been tried for reducing the effects of speckle in reconstructed holograms /4/. reconstruction with partially coherent illumination, either by using a small themal source or by using a laear source broadened by a moving scattering screen is one possibility. a second is to record the Image by scanning it with an
aperture of finite size compared to the speckle. a third is to move the pupil of the optical system which re-images the reconstruction and to time-average the resultant sequence of images. all these methods have some effect in reducing speckle contrast and all reduce the resolving power to some extent by acting as a low-pass filter on the Image. many variations have been described in the literature. the choice depends on the kind of images to be despeckled and on the nature of the detail which is important.
references
1. m.von laue. sitzungsberichte akad.wiss (berlin), 44,144,1914.
2. j.c.dainty. optica acta, 17, 761-772, 1970.
3. j.c.dainty. optica acta, 18, 327-339, 1971.
4. j.c.dainy, w.t.welford. optics communications, 3, 289-294, 1971.

