|
|
 |
 |

|
| |
ИНТЕРФЕРЕНЦИОННЫЕ ИЗМЕРЕНИЯ В ДИФФУЗНО-КОГЕРЕНТНОМ ИЗЛУЧЕНИИ НА ОСНОВЕ ТОПОГРАФИИ ИНТЕНСИВНОСТИ
Н.Г.Власов
Образование зернистой структуры, характерной для диффузно-когерентного излучения, на заседаниях школы было рассмотрено в лекции проф.Велфорда. В лекциях профессоров Лейта и Велфорда излагались способы устранения зернистой структуры, мешающей получить хорошее разрепение.
Однако этот отрицательный эффект, обусловленный избыточностью информации, становится положительным, когда мы переходим к интерференционным измерениям, которым и посвящена настоящая лекция. В ней рассматривается методика, являющаяся промеауточной меаду методами голографической интерферометрии и зернистой интерферометрии ( specle interferometry) а также делается сравнение упомянутых методов.
1. Введение несущей в голографию интенсивности в диффузно-когерентном излучении
Оптическая схема эксперимента, в которой реализуется предложенная методика, представлена на pиc.1a. Луч лазера вводится в оптическую систему зеркалом 3, коллимируется линзами Л1, Л2 и освещает объект О. Линза Л2 дважды используется в схеме: справа налево она действует как большая линза коллиматора, слева направо она производит преобразование Фурье плоскости предметов. В частотной плоскости расположен фильтр простраяственных частот Ф, состоящий из непрозрачного экрана с двумя круглыми отверстиями равного диаметра d /1,2/. Линза Л3 производит обратное преобразование Фурье и строит изображение исследуемого объекта в плоскости фотопластинки ФП.
В плоскости изображения волновое поле u(х , у) представим
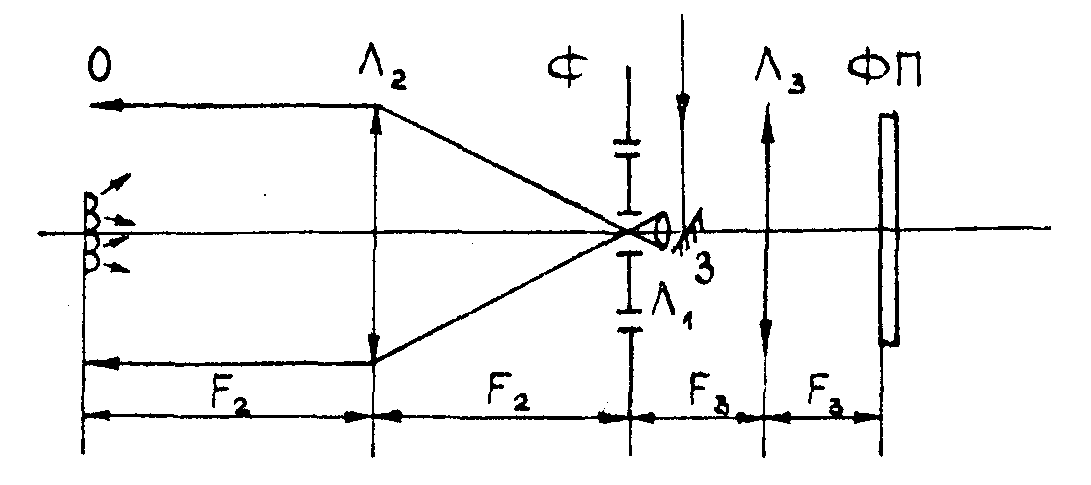
Рис. la. Схема записи голограммы интенсивности с несущей частотой в диффузно-когерентном излучении. Обозначения поясняются в основном тексте.
в виде произведения двух функций /3/: детерминированной функции координат t(х, у), характеризующей макроструктуру объекта, и случайной функции координат, характеризующей диффузное рассеяние на микроструктуре, разложив последнюю по плоским волнам:
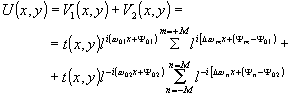 (1) (1)
В (1) ωi=2π/λ cosαi - пространственная частота, cosαi - направляющий косинус плоской волны; ω01 и ω02 - центральные пространственные частоты каадого из отверстий, вынесенные за знак суммы, Δωm= ωm- ω01, Δωn= ωn- ω02, Ψm, Ψn случайные функции пространственных частот. Разница в знаках первого и второго члена в правой части (1) определяется располодением отверстий по разные стороны от оптической оси. Величины m и Δωi+1- Δωi определяются теоремой отсчетов в оптике. Имея в виду,
что центры отверстий в фильтре пространственных частот расположены по оси x, для упрощения последующих расчетов считаем ω y= 0 . После записи на фотопластинку и восстановления, как и в любой голограмме, образуются дифракционные порядки, из которых +1-ый выпишем в явном виде:
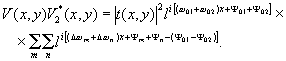 (2) (2)
Как видно из (2), восстановленное изображение пропорционально распределению интенсивности по объекту, а не амплитуде, как в обычной голографии, поэтому такие голограммы целесообразно называть голограммами интенсивности. Отметим, что возможно восстановление и в белом свете, как в голограммах сфокусированного изображения. Поясним образование несущей частоты более простыми рассуждениями. Наличие двух отверстий в частотной плоскости приводит к тому, что в плоскости изображения образуются два совпадающих изображения, каждое из которых является объективным по отношению к самому себе и опорным по отношению к соседнему. Изображения накладываются под углом друг к другу, в результате чего и возникает несущая. Это рассуждение подтверждается и при исследовании микроструктуры голограммы в микроскоп /1/: зернистая структура, средний размер которой ~f/d рассекается полосами несущей частоты (ω01+ω02) с периодом, обратно пропорциональным расстоянию между центрами отверстий.
Осуществим оптическую фильтрацию восстановленного изображения на основе двойного преобразования Фурье по схеме рис.16. Нулевой порядок дифракции расположен на оптической оси системы, в его центре находится яркая светящаяся точка, образованная восстанавливающим излучением, прошедшим голограмму без дифракции на ее микроструктуре. Математически нулевой порядок описывается суммой двух функций автокорреляции от каждого из отверстий в отдельности и близок к тому, который возник бы при наличии только одного отверстия в частотной плоскости при записи голограммы. Информация, заложенная в нем, исследуется в голографии сфокусированного изображения без опорного пучка, а соответствующая лекция на эту тему
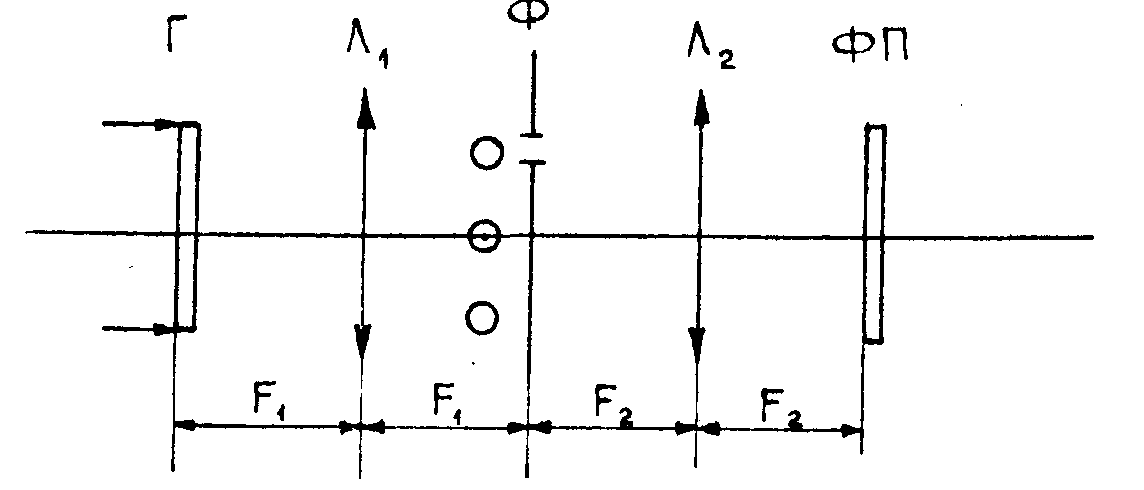
Рис.16. Схема фильтрации восстановленного изображения. Рядом с пространственным фильтром Ф схематически обозначены спектры 0+1 порядков дифракции.
будет прочитана И.С.Клименко. ±1-ые порядки дифракции описываются функциями кроскорреляции от совместного действия обоих отверстий. Распределение интенсивности в дифракционном порядке легко получить, воспользовавшись аналогией с радиотехническими процессами. Диффузно-когерентному излучению в радиотехнике соответствует белый шум, а его функция корреляции является треугольником. Таким образом, максимальная интенсивность приходится на центр дифракционного порядка и линейно уменьшается по радиусу от центра к краям. Более подробное описание можно найти в /4/.
Рассмотрим подробнее процесс фильтрации по схеме рис.16, основанный на использовании одного из первых порядков дифракции. Из выражения (2) видно, что центральной частотой первого порядка дифракции становится частота (ω 01+ω02), а весь диапазон ограничен частотами ±2ωМ. После первого преобразование. Фурье, осуществляемого линзой Л1 (рис.2), волновое поле в частотной плоскости описывается преобразованием Фурье от (2):
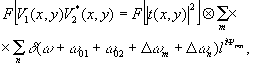 (3) (3)
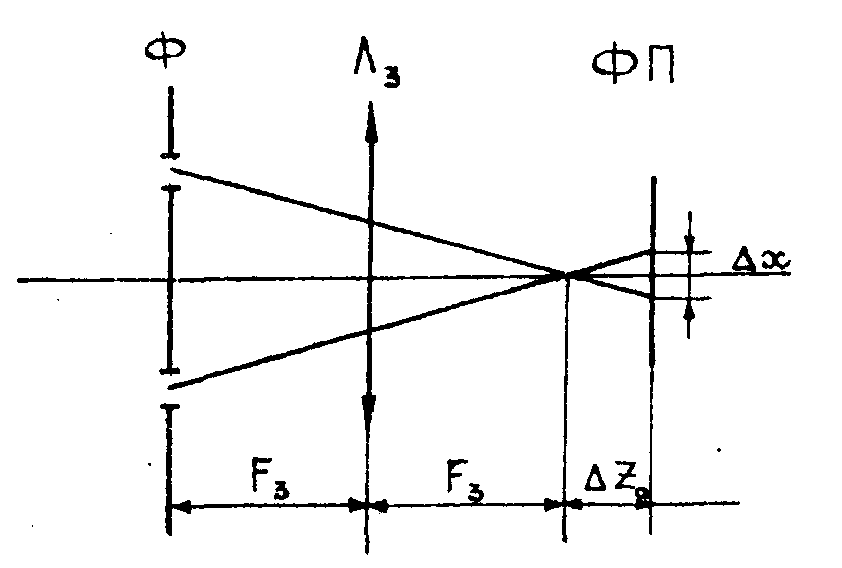
Рис.2. Показаны изменения в схеме рис.1 при переходе к интерферометрии сдвига. Пояснения в основном тексте.
Где [|t(x,y)|2] и ⊗обозначают преобразование Фурье и операцию свертки соответственно. Как видно из выражения (3), уменьшая диаметр отверстия в пространственном фильтре в процессе фильтрации восстановленного изображения, мы можем после обратного преобразования Фурье, осуществляемого линзой Л2, построить изображение в значительно более узком диапазоне пространственных частот, выбирая за центральную частоту любую из указанного диапазона. Экспериментально диапазон пространственных частот можно сузить на порядок, сохранив при этом достаточную интенсивность отфильтрованного изображения. Имея в виду эту возможность, проследим далее только за одним из сомножителей в выражениях (2),(3) при интерференционных измерениях методом двойной экспозиции, выбрав частоту (ω01+ω02). которую будем считать средней пространственной частотой узкого диапазона частот, в пределах которого интерферограмма на восстановленном изображении практически не изменяется (получение интерферограмм обсуждается ниже).
2. Распространение интерферометрии сдвага на диффузно-отражающие объекты
Применение сдвиговой интерферометрии к диффузно-отражающим
объектам считается в принципе невозможным. Действительно, при сдвиге, превышающем средний размер зерен зернистой структуры на восстановленных изображениях, сравнение двух сдвинутых изображений эквивалентно сравнению двух различных объектов. Микроструктура диффузно-отражающих объектов эквивалентна белому шуму в радиотехнике, а корреляция мекду двумя белыми шумами равна, как известно, нулю, что и делает прямые интерференционные измерения в принципе невозможными. Более подробно этот вопрос разобран в лекции Ю.И.Островского. Покажем, что изложенное ограничение не действует в рамках описываемой методики /5/. усложним несколько схему эксперимента на рис.1, выведя фотопластинку из плоскости изображения на расстояние Δz0 так, чтобы она не вышла из глубины резкости изображения, определяемой диаметром отверстия в фильтре пространственных частот и фокальными длинами линз f2 и f3 (рис.3). Тогда в плоскости фо-
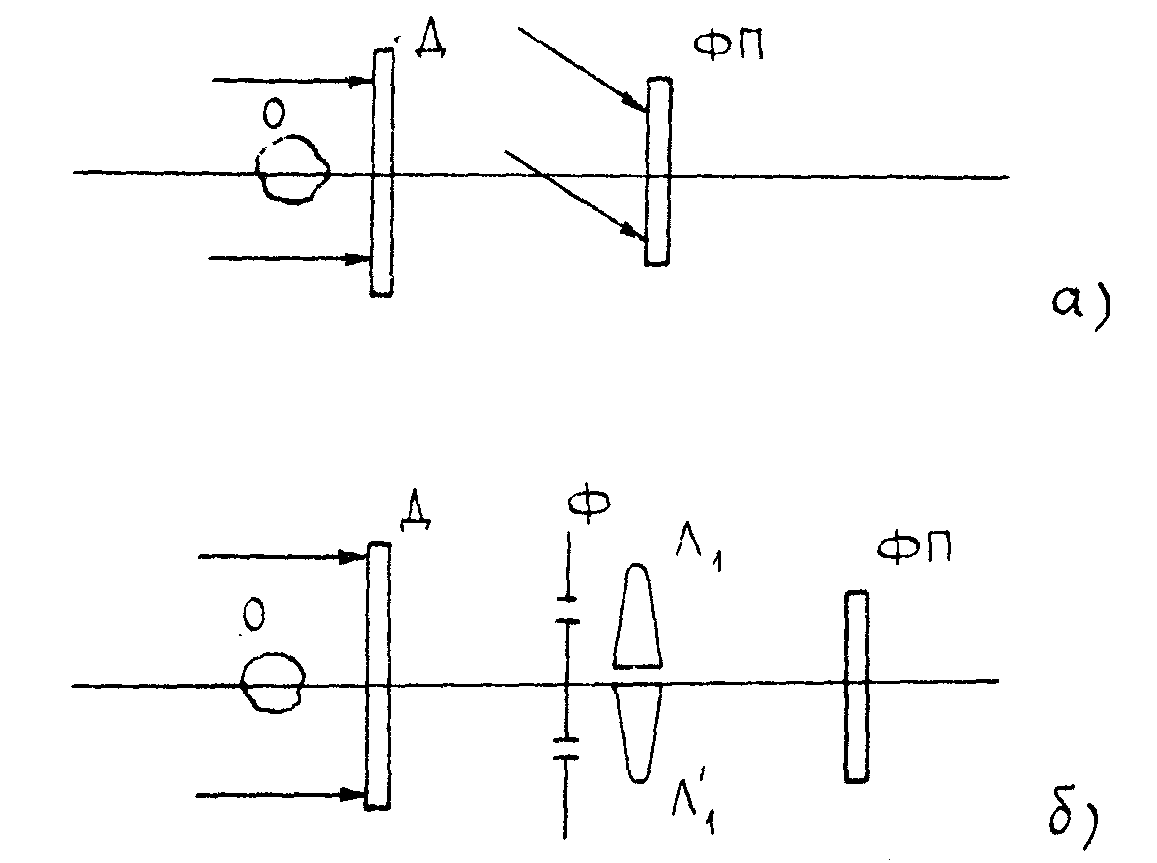
Рис.3. Схема исследования фазового объекта методом двойной экспозиции:
а) на основе голографической интерферометрии по обычной двухлучевой схеме;
б) на основе сдвиговой голографии интенсивности Л 1-Л'1 - билинза.
топластинки изображения смещаются относительно друг друга на величину Δх=Δх(ω 01, ω02, Δz0).
Как и оговаривалось выше, мы сейчас рассматриваем восстановленные изображения, созданные узким диапазоном пространственных частот с центральными частотами ω01 и ω02. Процесс записи проведем методом двух экспозиций, до и после приложения к объекту деформирующей нагрузки. Интенсивность, зарегистрированная фотопластинкой во время первой и второй экспозиции, соответственно, равна:
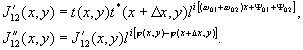 (4) (4)
В (4) φ(х,у) и φ(х+Δх,у) - детерлинированные функции координат, описывающие изменение, происшедшее с объектом меаду экспозициями, и зависящие, как известно, от пространственной частоты, на которой ведется регистрация или наблюдение /6/. Интенсивность изображения, восстановленного в первом порядке дифракции, равна:
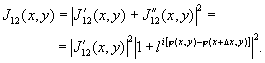 (5) (5)
Выражение (5) описывает интерферограмму сдвига, а сам интерференционный эффект, как и при записи голограммы по изложенной методике, обусловлен пространственной корреляцией по интенсивности. Вообще говоря, интерференционная картина образуется и при наличии только одного отверстия в частотной плоскости при записи голограммы и, соответственно, при использовании только нулевого порядка дифракции при восстановлвнии. Это - методика исследования зернистой интерферометрии, некоторые аспекты которой рассмотрены в лекции профессора Ингельстама.
Голограммы интенсивности с несущей, полученные экспериментально по описанной методике, по некоторым свойствам оказались близки к голограммам сфокусированного изображения (восстановление в белом свете), однако обладают значительно большей информацией.
Интерференционные полосы смещаются при изменении угла наблюдения в отличии от неподвижных полос в голограммах сфокусированного изображения. Выделяется интерференционная полоса нулевого порядка: она неподвижна и имеет максимальный контраст. При восстановлении в когерентном излучении при помощи описанного выше процесса фильтрации характер интерференционной картины на выходе оптической системы зависит от положения фильтра в частотной плоскости, а контраст интерференционных полос при фильтрации резко возрастает. Первый эффект объясняется тем, что характер интерференционной картины, а в нашем случае и величина сдвига зависят от пространственной частоты. Увеличение контраста объясняется тем, что уменьшая пространственным фильтром диапазон частот, мы увеличиваем область когерентности, пропорциональную λf/dф, где dф - диаметр фильтра. Отметим, что интерферограмма, описываемая уравнением (5), довольна сложна для расчета и может быть использована в основном для быстрых качественных оценок. Большой практический интерес представляют частные случаи уравнения (5), которые рассмотрим последовательно.
Зависимость величины сдвига от пространственной частоты можно устранить. Для этого возвратим фотопластинку в плоскость изображения, а линзу Лз в рис.1а заменим билинзой, установив ею требуемый сдвиг, который теперь не зависит от пространственных частот.
До сих пор речь шла о диффузно-отражающих объектах. Известно, однако, что методы их исследования на основе голографической интерферометрии могут быть перенесены на фазовые или зеркально-отражающие объекты, освещенные через диффузный рассеиватель /8/. Как пример приведем схему исследования фазового объекта, закрытого от голограммы диффузным рассеивателем /9/. На рис.3а,б представлены схемы исследования фазового объекта по работе /9/ и в варианте сдвиговой голографии интенсивности. По схеме рис.3б сдвиг одинаков для всех частот и определяется билинзой, создающей в плоскости фотопластинки два изображения диффузного рассеивателя. Функция φ(х,у) в обеих схемах по рис.За.б не зависит от пространственной частоты.
3. Выделение отдельных компонент вектора перемещения для диффузно-отражающих объектов /10/
Вернемся к схеме рио.1а, расположив отверстия в пространственном фильтре симметрично оптической оси. Как известно /6/, для диффузно-отражающего объекта φ(υ,у) имеет вид:
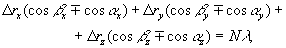 (6) (6)
где Δ ri - компонент вектора перемещения, βх и αх - углы между осями координат и направлениями освещения поверхности объекта и наблюдения (регистрации) восстановленного изобрааения,соответственно, n - порядок интерференции, знак " - " соответствует освещению и наблюдению по разные стороны от перпендикуляра к поверхности, " + " соответствует освещению и наблюдению с одной стороны. В голографической интерферометрии для расчета перемещения, заключающегося в определении Δrx, Δry, Δrz необходимо три интерферограммы и три уравнения вида (6). В нашем случае голограмма записывается двумя пучками, каждый из которых несет информацию об объекте, и регистрируется φ(х, у, ω)- φ(υ, у, -ω). С учетом этого (6) преобразуется в
2Δ rxcos αx=n xλ, (7)
т.к. αy=π/2 и cosαy=0. Таким образом, интерферограмма, описываемая (7), несет информацию только об одном компоненте вектора перемещения и практически не нуждается в дальнейшем расчете. Открывая в пространственном фильтре вместо отверстий по оси Х отверстия по оси У, можно по такой же методике выделить Δry, используя для этого ту же фотопчастинку. Если открыть четыре отверстия одновременно, то двойной экспозицией можно сразу получить отдельные интерферограммы для Δrx и Δry, однако дифракционная эффективность восстановленных изображений снижается из-за появления дифракционных порядков, несущих смешанную информацию о Δrx и Δry и описываемых перекрестными членами от совместного действия
вертикальных и горизонтальных отверстий в фильтре. Выделение на основе изложенной методики обсуждается в работе /10/. В /11 показано, что, применяя специальные схемы зернистой интерферометрии, также можно выделить Δrx, Δry, Δrz. Однако необходимо применение различных (и более сложных, чем приведенные) схем для выделения каждого из компонент вектора перемещения. Более подробное сравнение будет сделано ниже.
4. Регулировка чувствительности
Голографическая интерферометрия во многих случаях оказывается излишне чувствительной при исследовании реальных объектов (изделий). Регулировка чувствительности изменением величины сдвига очевидна, поэтому приведем формулы для φ(x, y, ω1)-φ(x, y, -ω2) и для φ(x, y, ω1)-φ(x, y, ω2), показывающие возможность регулировки чувствительности за счет изменения положения отверстий в фильтре пространственных частот по схеме риc.1а:
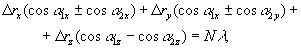 (8) (8)
где знак ± в множителях при Δ rx, Δry соответствует отверстиям по рfзные стороны и по одну сторону от оптической оси, соответственно.
З а к л ю ч е н и е
Проведем сравнение изложенной методики с методами голографичеокоя и зернистой интерферометрии. По сравнению с голографической интерферометрией мы сузили область применения для диффузно-отражательных объектов, ограничившись теми, чья кривизна поверхности достаточна для того, чтобы она могла быть передана линзами. Выиграли в возможности регулировать чувствительность; в стабильности схемы (это преимущество и по сравнению с некоторыми методами зернистой интерферометрии): в лабораторных условиях можно получать интерферограммы, не заботясь о защите оптической схемы от вибраций. Не
нужен также одномодовый режим лазера. Малый угол между интерферирующими пучками позволяет использовать фотоэмульсии с меньшим разрешением. В зернистой интерферометрии требования к разрешению фотоэмульсии снижаются еще больше, однако по сравнению с ней мы выиграли в том, что избавились от нерассеянной части восстанавливающего пучка, и можем получать изображение объекта и,соответственно, интерферограмму на любых пространственных частотах, участвовавших в процессе записи; упростились схемы выделения отдельных компонент вектора перемещения и регулировки чувствительности. В отличие от любого другого интерференционного метода появилась возможность распространить интерферометрию сдвига на исследование диффузно-отрадающих объектов.
Отметим, что схема записи голограмм интенсивности на основе двойного преобразования Фурье требует линз большого диаметра, что ограничивает размер исследуемых объектов. Объекты больших размеров можно записывать, используя только одну линзу или объектив с пространственным фильтром, расположенным непосредственно перед .линзой (объективом). Тогда интерферограмма будет нести информацию Δrx, Δry, Δrz одновременно и описываться выражением (8).
Л и т е р а т у р а
1. duffy. appl.opt., 11, 8, 1778, 1972.
2. Н.Г.Власов, Ю.П.Пресняков, в сб."Оптическая голография", изд.ЛДН ТП, Ленинград, 1972.
3. s.lowenthal, h.arsenault. josa, 60, 11, 1970.
4. j.m.burch, j.m.j.tokarski. opt.acta, 15, 2, 101, 1968.
5. Н.Г.Власов, Ю.П.Пресняков. Квантовая электроника, 1973. № 2(14).
6. Е.Б.Александров, А.М.Бонч-Бруевич, Ж.Т.Ф , 37, №2, 360-369, 1967.
7. Н.Г.Власов, Ю.П.Пресняков, в сб."Современное соотояние и перспективы высокоскоростной фотографии и кинематографии и метралогии быотропротекащих процессов".
8. Н.Г.Власов, Ж.Т.Ф., 40, №8, 1656-1659, 1970.
9. f.c.jahoda et al. appl.opt., 6, 8, 1407, 1967.
10. Н.Г.Власов, Ю.П.Пресняков, С.Н.Смирнов, ЖТФ, №5, 11 04-1106, 1973.
11. j.a.leendertz. j.sci.instrum., 3, 214, 1970.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

