methode de traitement optique de l' information par interferences eh lumiere diffuse
m.l.roblin universitée de paris vi, laboratoire d'optique, france
l'existence de phénomènes d'interférence en lumière diffuse a été signalée pour la première fois par newton /1/,dans son expérience une source lumineuse ponctuelle est places au centre de courbure d'un miroir dont la face arrière est réfléchissante; il apparait alors un système d'anneaux colorés autour de la source.
le duc de chaulnes /2/ reprend en 1955 las expériences de newton; il rend diffusante la première face du miroir, et montre que le contraste se trouve ainsi amélioré.
d'autres ont par la suit étudié des expérinces comparables. par exemple fabry et perot /3/ obtiennent un phénomène analogue en lumière transmise avec une lame plan parallèle dont l'une des faces est rendue diffusante, l'autre étant semi-réfléchissante.
l'application de cephénomène a 1'interférométrie a été réalisée par burch; il décrit en 1953 /4/ un interféromètre formé de deux diffusants identiques placées symétriquement par rapport au centre de courbure d'un mirroir, ce système permet de mettre en évidence les défauts de surface de ce mirroir. les diffuseurs utilisés transmettent une partie de l'onde incidente et diffusent l'autre partie: les interférences ee produieent entre deux ray-ons lumineux diffractes par chacun des diffuseurs en des points homologues, et transmis par l'autre diffuseur.
les phénomènes d'interférence en lumière diffuse sont observés également en holographie, où l'intarprétation des franges en interférometrie holographique falt l'objet de nombreux travaux: dans ce cas encore les franges résultent des interférences pro -
duites par deux diffusants - ou éléments de diffusant - identiques et déplaces l'un rapport à l'autre /5/.
nous utiliserons dans toutes nos expériences un phénomène d'interférence lia à une translation entre deux surfaces diffusantes identiques-éclairées par une source ponctuelle. les franges sont alors localisées dans lo plan de la source luminouse, en particulier si l'on enregistre sur une même plaque photographique plusieurs images décalées d'une même répartition aléatoire d'intunaité, on observe, en éclairant par une onde plane, des franges rectilignes à l'infini. burch rt tokaraki ont étudié en 1968 ce phénomène /6/.
nous avons utilisé systématiquement lea franges d'interférences résultant de tranolation d'un système diffusant pour des expériences de traitement optique de l'information. nous donnerons d'abord les principes généraux commune a toutes ces expériences, puis las différentes applications.
principe general
dans la plupart des expériences effectuées dans notre laboratoire (à l'exception de 1'interférometrie différentielle) l'objet a est un objet plan a transparence variable, en géenéral un cliché photographique. on enregistra eur une plaque photographique h le produit de la transparence a(
η, ξ) de l'objet par une transparence aléatoire d(η, ξ), à haute fréquence. (η, ξ) représentent les coordonnées d'un point do la plaque.
- la montage utilisé pour l'enregistrement est schématisé sur la figure 1. on forme l'Image de l'objet a sur une plaque
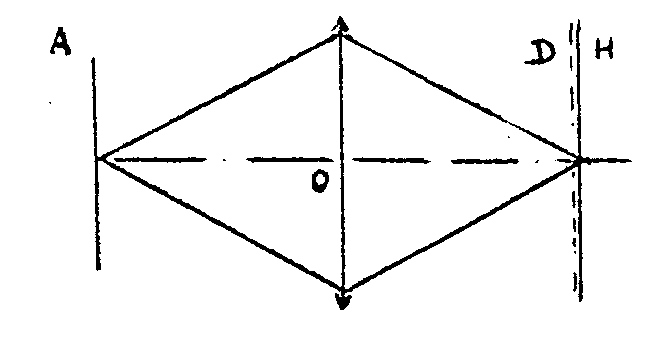
figure 1.
photographique h, par l'intermédiaire d'un diffuseur d placé au contact de h. on enregistre ainsi le produit a x d. après développement de la plaque dans les conditions habituelles, sa transparence est une fonction linéaire du produit a x d.
le montage utilisé pour les différentes opérations de traitement optique est schématisé sur la figure 2. la plaque photo-
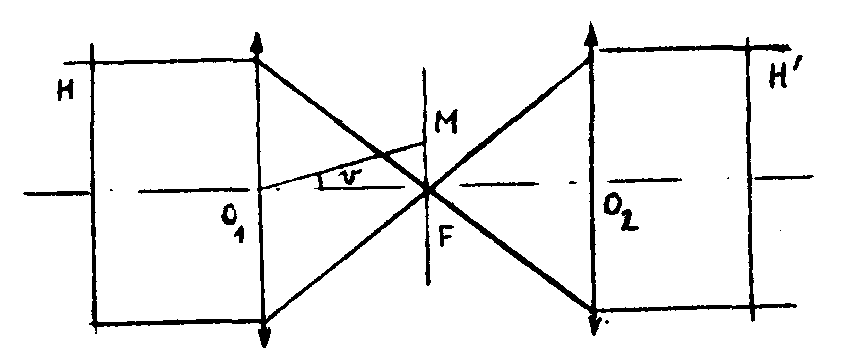
figure 2.
graphique h, éclairée en onde plane, est placée dans le plan focal objet de l'objectif o1. on obtient en f la transformée de fourier de l'amplitude transmise par h. en dehors de l'Image directe de la source, focalisée au centre du plan focal, le spectre observé est le produit de convolution de la transformée de fourier de a par la transformée de fourier de d. le spectre de a est voisin d'une fonction
δ; le spectre de d est, au contraire, largement étalé dans le plan considéré. tout se passe comme si la tache de diffraction définissant l'objet se trouvait répétée, avec des coefficients variables, en tout point du plan focal. on pourra donc reconstituer dans le plan h' l'Image de a en utilisant par filtrage une zone quelconque du plan f.
le phénomène d'interférence utilise pour moduler ce spectre est réalisé de la manière suivante. lors de l'enregistrement (figure 1) on effectue successivement sur la même plaque h deux on plusieurs poses entre lesquelles on donne à h un déplacement de faible amplitude (le déplacement total devra être suffisamment petit pour que l'Image de l'objet ne soit déplacée d'une
façon sensible dans les conditions d'observation utilisées).
si l'on effectue deux poses, la plaque h enregistre une intensité qui est le produit de convolution de (a x d) par la somme de deux fonction δ: le spectre dans le plan f sera modulé par des franges à 2 ondes.
2 - supposons maintenant que l'on effectue 2n + 1 poses successives avec un décalage ξ0 constant. l'intensité enregistrée est alors
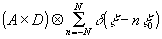
(où n est un nombre entier)
- dans le plan y obtient, si n est infini, une modulation du spectre par un peigne de dirac sous la forme
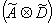 peigne (v/v0)
peigne (v/v0)
ou v représente l'abscisse angulaire d'un point du plan focal. l'intervalle entre doux pics est v0
= λ/ξ0 .
si n est fini, les maximums principaux sont élargis et il apparait des maximums secondaires. ce phénomème peut être gênant mais il est possible de supprimer cet effet en utilisant des temps de pose successifs proportionnels aux coefficients du binôme (burch et tokarski /5/).
la modulation est ainsi réalisée dans le plan du spectre; on voit qu'il est possible, par filtrage dans ce plan (par une fente, ou une grille) de faire apparaître ou disparaître l'Image de l'objet suivant qu'on utilise des maximums ou des minimums de la figure d'interférence.
les différentes applications que noua avons étudiées sont:
1- différence entre deux images
2 - inversion de contraste
3 - stockage d'informations
4 - réalisation d'une Image colorée à partir d'un cliché en et blanc.
5 - interférométrie différentielle.
1.etude de la différence entre deux images /7/
de nombreux procédés sont employés pour déceler les détails différents entre deux clichés, pris en général à des instants différents. cette détermination est utile en particulier en médecine (comparaison de radiographies) ou en météorologie (déplacement de formations nuageuses) et dans de nombreux autre domaines, par exemple en astronomie (émissions spectrales différentes).
nous donnons ici le principe de la méthode basée sur les interférences en lumière diffuse.
la figure 3 illustre la technique d'enregistrement des deux
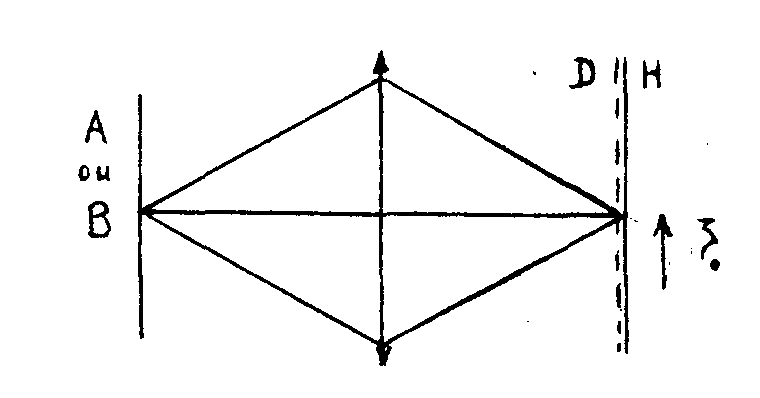
figure 3.
images; soient a et b les transparences des deux images, d le diffusant. dans une première pose on enregistre le produit axb, dans la seconde pose on enregistre b x d après avoir déplacé la plaque h de ξ.
la différence cherchée est caractérisée par b = b - a. en tenant compte de cette définition l'intensité enregistrée est de la forme
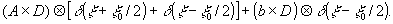
dans le plan f, indépendamment de l'Image directe de lasource, la répartition d'amplitude est alors de la forme
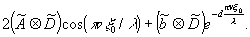
une tante placée dans le plan f
en un poit v tel que cos(πvξ0/λ)=0 élimine le premier terme, et la transformée de fourier du second ternie donne l'Image en h' sous la forme b x d, c'est - àdire la différence cherchée.modulée par le diffuseur.
en réalité l'expérience ne donne pas de bons réaultets dans ces conditions. en effet, si l'on prend une fente relativement large, le premier terme n'est pas nul, et la zone commune reste visible, bien quatténuée; avec une fente très étroite le"grain" du au diffusant eet accru l'Image définitive. il est done nécessaire d'obtenir un minimum nul plus étendu afin de pouvoir utiliser une fente plus large.
l'expérience sera donc réalisée avec des poses multiples. pour 3 poses, i' Image b est utilisée une seule fois avec un temps de pose 1; l'Image a est enregistrée en deux poses avec un déplacement égal de h de part et d'autre, ξ0, et un temps 0 de pose moitié.
l'amplitude correspondante dans le plan f est alors
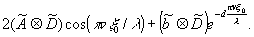
la figure 4 permit de comparer les résultats obtenus avec 2 et 3 poses. la courbe en traits pointillés représente les variations de l'amplitude dans le plan s du terme correspondant à la
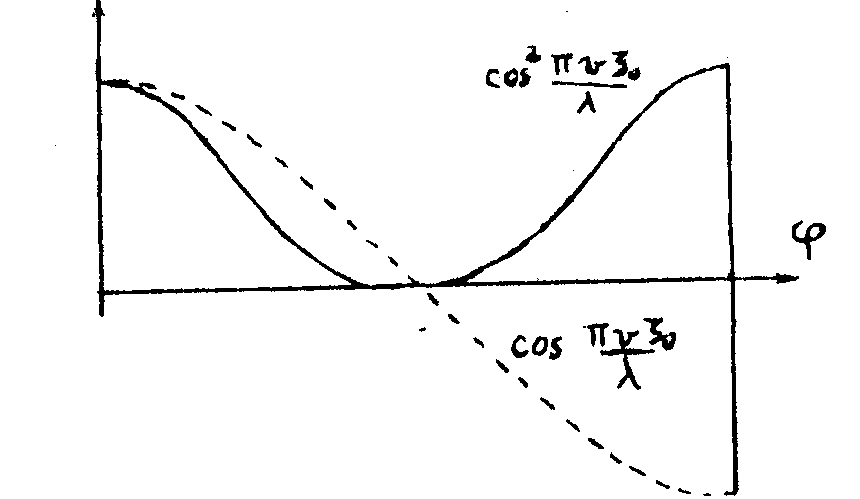
figure 4.
partie commune a pour 2 poses; la courbe en traits pleins correspond au cas de 3 poses. la modulation est en et les variations au voisinage du 0 sont beaucoup plus lentes. la formule obtenue pour l'amplitude en f pour un nombre n(pair) de translations, correspondant à un nombre n+1 de poses, est de la forme
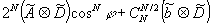
ou
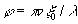
le spectre correspondant à la partie commune est multipliée par cosn
φ.
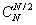 est un
coefficient du binôme. le minimum nul est d'autant plus plat que n est
plus élevé.
est un
coefficient du binôme. le minimum nul est d'autant plus plat que n est
plus élevé.
on a ainsi le moyen, par des poses multiples, d'obtenir de bons résultats par filtrages. cependant la réalisation expérimentale devient alors plus délicate; la mise au point de cette méthode est actuellement en cours dans notre laboratoire.
2.inversion de contraste d'un cliché
nous n'insisterons pas sur ce procédé, qui peut être considéré comme un cas particulier de l'expérience précédente; en effet, il suffit de prendre, si a est le cliché utilisé, un objet b de transparence constante égale à la transparence maximale de a. en appliquant la méthode précédente, on obtiendra dans le plan h' une valeur b-a de l'amplitude qui bien, par rapport au cliché d'origine, un négatif. en réalité l'intensité observée est (b-a)2, et il faut donc prendre b supérieur ou égal à la transparence maximale de a.
dans cette expérience, comme dans la précéd-inte, l'utilisation de poses multiples est favorable.
l'opération d'inversion de contraste est cependant plus simple à effectuer que la différence entre deux images trés voisines, la position relative des images a et b n'ayant pas d'importance.
3. stpockage d'informations /8/
la méthode décrite permet également d'enregistrer sur une même plaque photographique plusieurs images que l'on peut ensuite reproduire séparément, sans superposition, à l'aide d'un filtrage convenable. l'étude générale nous a montre que pour un objet donné a le spectre du produit a x d est modulé par des franges dont la fréquence ne dépend que du déplacement élémentaire
ξ0 entre deux poses successives. en admettant que la loi de modulation permette d'obtenir des pics séparée par des miniœud nuls l'Image de a ne pourra être obtenue que si le filtre utilisé laisse passer l'un au moins des pics correspondants. si plusieurs objets, a,b,.... sont codés avec des déplacements suivant l'objet considéré, on peut donc en déplaçant une fente dans le plan f obtenir successivement l'Image en h' de l'un ou l'autre des objets enregistres.
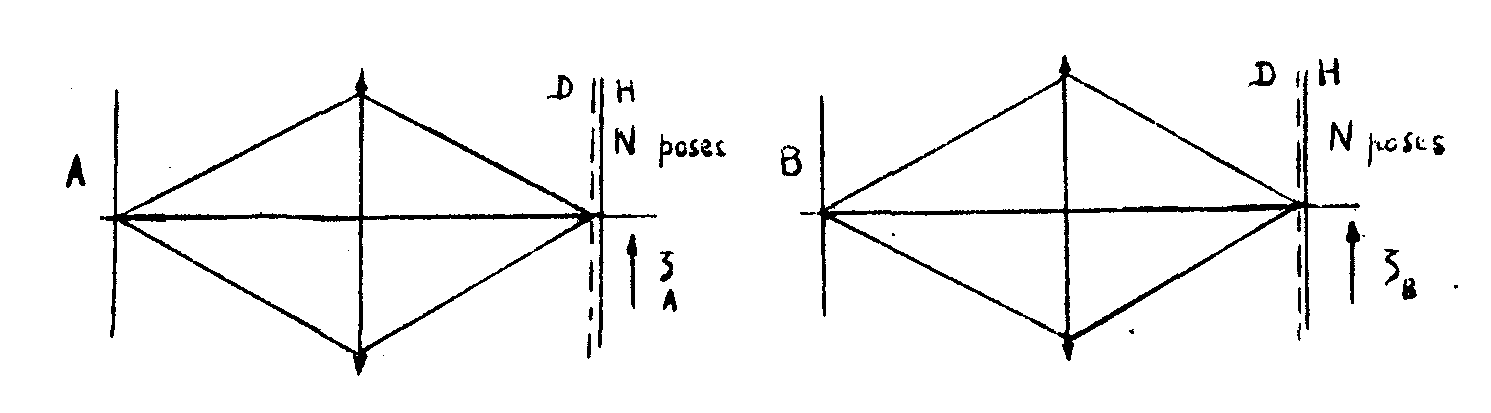
figure 5.
la figure 5 donne le principe de l'expérience pour drux objets. dans un premier temps, on enregistre l'objet a, avec un nombre h de poses effectuées avec des temps déterminés, et un déplacement élémentaire ξa. on répète l'expérience avec l'ob-
jet b dana les mêmes conditions, mais avec un autre déplacement élémentaire ξ0. pour obtenir des minimus nuls, on utilise encore les coefficients du binôme pour les temps de pose successifs, et un nombre h assez grand. on doit en effet avoir des pics très étroits afin de pouvoir enregistrer le plue grand nombre possible d'images.
l'amplitude dans le plan ou s'effectue le filtrage s'écrit, toujours en négligeant l'Image centrale
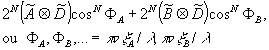
comme dans le cas précédent, l'expérience est délicate si l'on effectue un grand nombre de déplacement.
autre forme de codage /9/:
nous avons utilisé jusqu'à présent le phénomène d'interférence produit en déplaçant le diffuseur dans son plan. cette expérience peutêtre effectuée à 1'enregistrement avec un diffuseur quelconque, et une lumière non cohérente. le seul élémentutile est en effet la répartition aléatoire d'intensité dans le plan de la plaque photographique. un autre type de codage est possible; il faut alors utiliser un diffuseur particulier (obtenu photographiquement) et un éclairage cohérent a 1'enregistrement. la figure 6 illustre oe nouveau type d'enre-
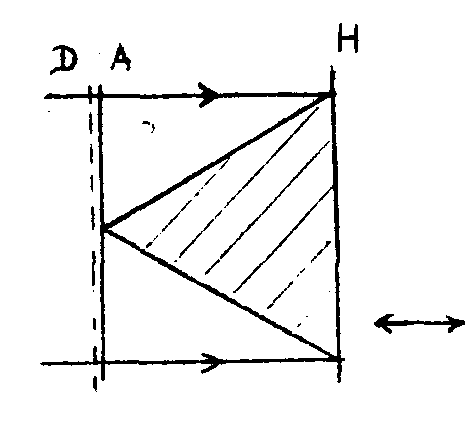
figure 6.
gistrement.
le diffuseur d, placé contre l'objet a, donne une onde directement transmise servant d'onde de référence; on réalise ainsi un véritable hologramme de l'objet axd. on effectue alors plusieurs poses successives en donnant à la plaque h, entre deux poses, des déplacements égaux dans la direction normale. a la reconstruction, le montage est identique àoelui utilisé jusqu'à présent (figure 2). l'hologramme h éclairé par une onde plane donne deux séries d'images-réelles et virtuelles - de l'objet a x d, décalées en profondeur. on obtient alors dans le plan de
pourier une amplitude modulée par des anneaux à ondes muitipies. en utilisant des déplacements longitudinaux différents, on peut ainsî enregistrer plusieurs objet que l'on filtrera ensuite par des grilles circulaires convenablement choisies.
le problème habituel de la séparation des images réelles et virtuelles est ici facilement résolu; en effet si le déplacement de la plaque est effectué dans une direction faisant unoangle cl aveo la normale, on obtient dans le plan de fourier deux systèmes d'anneaux décentrée d'un angle 2α et correspondant respectivement aux images réelles et virtuelles, le filtrage par une grille annuaire permet d'utiliser un seul de ces systèmes.
4.observation d'une Image en couleur à partir d'un cliché noir et blanc /10/
il est toujours possible de réaliser une Image colorée à partir de trois clichés en noir et blanc, que l'on éclaire avec trois longueurs d'onde différentes, et dont on superpose les images. houe pouvons effectuer cette opération en enregistrant sur une plaque photographique h avec un codage convenable de chacune d'elles, les images relatives aux trois langueurs d'onde utilisées.
los trois clichés en noir et blanc seront obtenus en plaçant dea filtre différents lors de la prise de vue de l'objet en couleur. pour simplifier l'exposé nous supposerons que l'expérien-
ce est effectuée pour deux longueurs d'onde λr et λb (rouge et bleu par exemple). soient ar, et ab les transparences des clichés correspondants.
on enregistre successivement sur la plaque h, comme dans le cas du stockage d'informations décrit précédemment, le produit ar x d avec un décalage ξr, puis le produit ab x d, avec un décalage différent ξb: notons que si l'on a réalisé séparément les clichés de transparence ar et ab pour servir d'objets dans l'expérience, celle-ci peut etre effectuée à l'enregistrement avec une longueur d'onde quelconque, le déplacement étant obtenu au niveau de la plaque photoqraphique h.
a la reconstitution, on éclaire simultanément la plaque photographique ii avec deux ondes planes de longueurs d'onde λa et λb.
supposons que le système modulant le spectre soit un peigne de dirac. on obtient pour chaque déplacement particulier deux peignes de dirac correspondant aux deux longueurs d'onde figure 7. dans le cas considéré on obtiendra donc pour l'objet ar
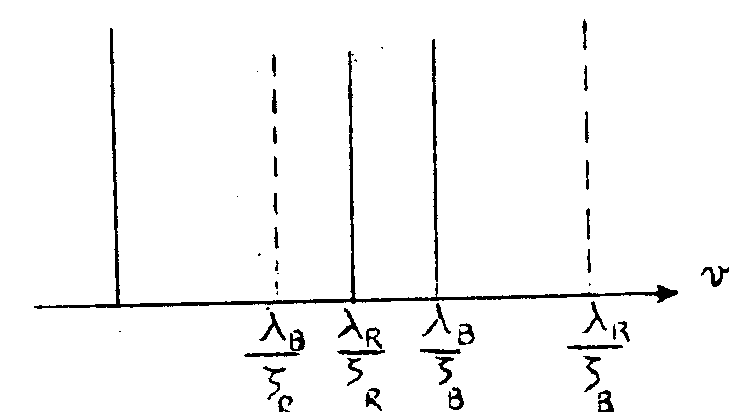
figure 7.
les positions λ
r/
ξr,
et λb/
ξb des pics et pour l'objet a
b les positions λr/
ξr et λb/
ξb. par une diaphragmation convenable, on conserve seulement les pics λr/
ξr et λb/
ξb et on forme donc en h' une Image (a
r x d), avec la longueur d'onde λr, et (a
b x d), avec la longueur d'onde λb, ce qui donne bien le résultat cherché. le raisonnement est
naturellement identique avec trois longueurs d'onde, à condition de définir trois déplacements différents.
on peut utiliser des déplacements ξ proportionnels aux longueurs d'onde reapectivea; tous les pics utiles sont alors confondus dans le premier maximum, commo dans tous les autres. on peut alors effectuer le filtrage avec une seule fente, ou une seule grille à traits équidistants.
5. interféromètre djfférential /11,12/
dans les expériences précédentes, le système d'interférences est un simple codage, que l'on intodult indépendamment de l'objet. appliqué aux différents objets étudiés il nous a permis soit d'obtenir ces objets séparément (stockage d'information), soit de superposer certains d'entre eux sélectivement (codage des couleurs), soit de les retrancher (différence entre deux images). dans l'expérience que nous allons maintenant décrire, le phénomène qui produit les interférences est lié à l'objet lui-même, o et la caractérise. le filtrage permet alors d'obtenir des informations sur cet objet particulier. hais, pratiquement, l'observation s'effectue dans les mêmes conditions de montage, et un phénomène d'interférence du même type se produit dans le plan de fourler.
nous étudierons deux montages d'interférométrie différentielle. ces montages donnet en définitive les mêmes informations, mais différant par la technique d'enregistrement.
premier montage:
inexpérience est basée sur le principe suivant (figure 8).
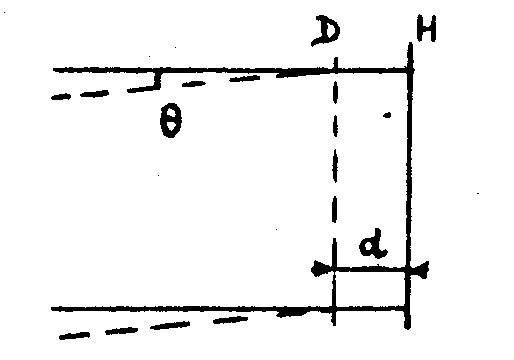
figure 8.
le diffuseur d - qui peut être par exemple un verre dépoli-éclairé par une onde plane perpendiculaire à son plan produit sur une plaque photographique h placée à une faible distance d du diffuseur une répartition aléatoire d'in tensité. cette intensité est enregistrée sur h. on incline ensuite l'onde incidente d'un petit angle θd . on peut montrer que l'intensité obtenue sur la plaque photographique est décalée, par rapport à la précédente, d'une qualité θd. on réalise ainsi, la plaque photographique restant fixe, un déplacement du système enregistré proportionnel à l,angle θ. il faut noter toutefois que ceci n'est vérifié que pour de faibles valeurs de li'angle /13/.
cette propriété est utilisée dans le montage suivant (figure 9). une première pose est effectuée avec une onde plane no-
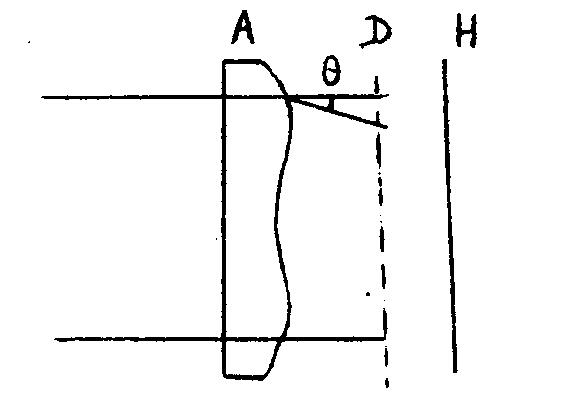
figure 9.
rmale éclairant le diffusant d. une deuxième pose est effectuée en plaçant sur le trajet de l'onde incidente un objet de phase a. en chaque point, l'objet de phase peut être considéré comme un prisme de petit angle, introduisant sur l'onde incidente une déviation θ, et au niveau de la plaque photographique une translation θd. si l'objet a, le diffusant et la plaque photographique sont placés. des distances assez faibles, on peut faire correspondre à une zone déterminée de pente constante sur l'objet une zone déterminée de la plaque photographique; dans ces conditions, on peut définir en chaque point de la plaque photographique h une valeur ξ, du décalage.
après développement, la plaque photographique est éclairée par une onde plane (figure 10). le déplacement θ, défini pour une déterminée de la plaque, produit dana le plan f un phénomène d'interférence d'intensité cos2kvξ/λ ou v représente l'abscisse angulaire d'un point. ξ étant variable d'un point à l'autro de h, lea phenomènes d'interférerue relatil's à chaque zone se détruisent ot l'on n'observe pas de franges dans le plan focal. cependant, si l'on forme l'Image de par 1'intermédiaire d'une ouverture t, placée au point d'abscisse v du plan focal l'intensité lumineuse en chaque point de l'Image de h est multipliée par cos2(kvξ/λ) et l'on observe donc sur l'Image de h' des franges correspondant à des valeurs égales de ξ, dono du dédoublement angulaire propre à l'objet, iin définitive, ces frangée dessinerait donc les lignes d'égale pente de l'objet do phase.
la méthode utilisée met doue en évidence la dérivée de la phase par rapport à une direction définie par la position de l'ouverture t dans le plan focal. la sensibilité du dispositif est fonction de la valeur de v donc de la distance du point t au centre du champ.
si l'observation est faite en lumière blanche, et pour de faibles variations de phase de l'objet, on aura avantage à placer t au voisinage de la teinte pourpre (qui correspond à un minimum pour le système d'interférence du au déplacement moyen); l'oeil étant alors très sensible aux variations de teintée décèle ainsi de très faibles différences.
nous allons maintenant décrire le deuxième montage qui no difère du précédent que par la technique d'enregistrement, l'exploitation du cliché étant la même.
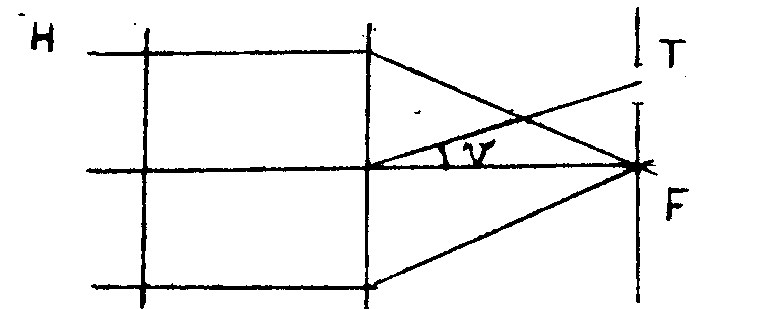
figure 10.
deuxième montage (figure 11)
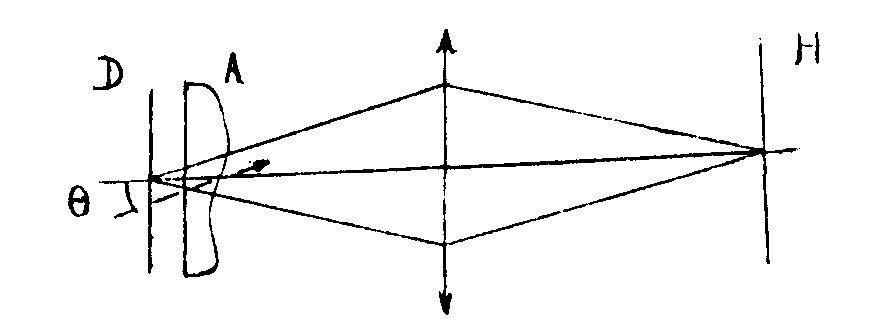
figure 11.
on forme sur la plaque photographique h l'Image du diffuseur d.i1 n'est plus nécessaire d'utiliser une source rigoureusement ponctuelle l'Image sur h pouvant être définie en éclairage incohérent. l'objet de phase a, placé après le diffusant à une distance d, produit un déplacement latéral de l'Image de d qui varie avec le point considéré, et qui est proportionnel à θ d (ou θ est encore la déviation angulaire produite par a au point considéré). on effectuera deux poses, avec et sans l'objet a, comme dans le cas précédent, et l'utilisation du cliché obtenu est naturellement la même.
notons cependant que la sensibilité de la méthde est maintenant liée à la distance d entre l'objet et la diffuseur, qui doit cependant rester faible pour qu'on puisse établir une correspondance entre un point de l'objet et un point du diffuseur;
il faut tenir compte également de l'ouverture du système optique formant l'Image de d pi'or définir la distance d tolérable.
il y a d'ailleurs lieu de tenir compte dans ce montage du défaut de mise au point introduit par l'épaisseur moyenne de l'objet (s'il s'agit d'un objet matérialisé: lane de verre ou lentille); ce défaut de mise au point moyenentraine la disparition du système de franges. il suffit, pour éviter ce brouillage distance d entre l'objet et le diffuseur (l'une d'entre ellea correspondant par exemple à d = 0).
do ernier montage doit être rapproché d'une expérience précédente /12/ où le diffuseur était remplacé par un réseau ronchi. entre les deux posée le réseau était déformé par l'objet de phase, produisant sur la plaque photographique h des franges de moiré. si l'on éclaire h par une onde plane, l'observation doit entre faite en plaçant un diaphragme dans la plan de fourier, dans le premier ordre diffracté par le réseau.
dans le cas du réseau en effet, le spectre se compose de quelques fonctions δ particulières, et la sensibilité du dispositif est définie à la prise de vue par la fréquence du réseau.
l'Image du diffuseur peut être considéré, au contraire, comme la superpositions d'une infinité de réseaux de fréquences et orientations variées; ceci nous permet de placer t en un point quelconque du plan f, celui-ci correspondant toujours à une fréquence perticulière du diffuseur. l'avantage du diffuseur vient donc du fait qu'il nous permet de disposer simultanément sur un même cliché de toutes les directiond et toutes les fréquences, et d'étudier ainsi la dérivée de la phase par rapport à une direction quelconque. en revanche, l'Image finale se trouve perturbée par la présence de différentes fréquences à l'intérieur même de l'ouverture t; qui se traduisent par un aspect granuleux de l'Image.
en conclusion, l'utilisation d'une modulation aléatoire du signal offre de grandes possibilités dans le domaine du traitement optique de l'information. l'enregistrement et le codage des images peuvent se faire dans la plupart des cas avec une lumière relativement peu cohérente; d'autre part il est facile de réaliser un diffuseur qui peut stre par exemple un simple verre dépoli. le seul inconvénient est la persistance d'une modulation d'intensité d'ue au diffuseur au niveau de l'Image définitive. on peut atténuer cet effet en utilisant des diffuseurs à structure très fine, offrant un spectre très étendu. cependant la structure dans l'Image dépend essentiellement du diaphragme utilisé pour le filtrage. l'Image du diffuseur est en effet la convolution de d par la tache de diffraction du diaphragme de fil-
trage. il est donc plus avantageux, dans la mesure du possible, de filtrer non par une fente, mais par une grille placée dans le plan de fourier: à ce moment là c'est la dimension totale de la grille qui détermine la tache de diffraction élémentaire, et non plus largeur d'une seule fente.
r e f e r e n c e s
1. newton. optics, 4ème édition, c.bell arid sons, ltd., londres, p.189, 1931.
2. duc de chaulues. mém. de l'anc. acad. des sc., p.136, 1755.
3. g.fabry, r.perot. annales de chimie et de physique, 7ème série. tome 12, 1897.
4. j.m.burch. nature, 171, 889, 1953.
5. c.froehly, j.monneret, j.pasteur, j.c.vienot. optica acta, 16, 3, 343, 1969.
6. j.m.burch, j.m.j.tokarski. optics acta, 15, 2, 1968.
7. s.debrus, m.francon, c.p.grover. optice communications, 4, 2, 172, 1971.
8. c.p.grover. j.o.s.a., 62, 9, 1-71, 1972.
9. a.lifchitz, m.may. optics acta, 19, 3, 187, 1972.
10. c.p.grover. optics communications, 6, 3, 258, 1972.
11. s.debrus, m.francon, c.p.grover, m.may, m.l.roblin. appl.optics, 11, 853, 1972.
12. s.mallick, m.l.roblin. optics communications, 6, 1, 45, 1972.
13. s.debrus, c.p.grover. optics convriunications, 3, 5, 340, 1971.

