|
|
 |
 |

|
| |
ПРОБЛЕМА НЕЛИНЕЙНОСТИ В ГОЛОГРАФИЧЕСКОМ
ИЗОБРАЖЕНИИ
Г.Б.Семенов
Нелинейность голографической записи обсуждается с точки зрения ее влияния на качество восстановленного изображения. Рассмотрен ряд особенностей так называемых изображений высшего порядка и приведены некоторые примеры использования изображений высшего порядка для решения практических задач.
Известное свойство голограммы восстанавливать неискаденный волновой фронт было сформулировано Габором в предположении, что фотоматериал, на котором регистрируется голограмма, обрабатывается до величины коэффициента контрастности γ = -2 /1/. При этом амплитудная прозрачность голограммы оказывается пропорциональной интенсивности излучения, экспонирующего фотоматериал в процессе регистрации такой голограммы. Аналогичное предположение о линейной связи между амплитудной прозрачностью голограммы и интенсивностью экспонирующего ее излучения было использовано в работах Лейта и Упатниекса /2-4/ и в работах ряда других авторов, которые также связывали факт восстановления голограммой неискаженного трехмерного изображения объекта с существованием линейной связи между названными выше величинами. Лейт и Упатниекс предложили также ввести новую характеристику для фотоматериалов, используемых в голографии, а именно: зависимость амплитудной прозрачности материала от экспозиции и рассматривали линейную запись голограммы как запись, осуществленную в пределах линейной части такой кривой /2/. Типичный вид подобной характеристики для галоидо-серебряной эмульсии изображен на рис.1. На этом же рисунке для сравнения изображена широко используемая в фото-
графии характеристическая кривая, которая представляет собой зависимость оптической плотности d от логарифма экспозиции. Н. Отметим, что неудобство такой характеристики для фотоматериалов, используемых в голографии, состоит в том, что ее линейный участок приходится как раз на нелинейную часть характеристики t=f(Н).
Для существующих фотоматериалов протяженность линейного участка кривой t=f(h) весьма невелика, а потому линейная запись голограмны может быть осуществлена при малых отношениях интвнсивностей объектного и референтного пучков. Это, в свою очередь, ограничивает дифракционную эффективность голограмм, а следовательно, и яркость восстановленного изображения.
Помимо практических соображений, отмеченных выше, вопрос о нелинейной регистрации голограмм имеет и большое научное значение, поскольку он непосредственно связан с процессом образования изображения в голографии. В частности, тот хорошо известный факт, что даже при сильной нелинейности регистрирующей среды голограмма сохраняет способность восстанавливать изображение, играет исключительную роль в голографии. Именно благодаря этому свойству голограмма может быть зарегистрирована на обычных фотографических материалах.
В настоящем докладе мы обсудим проблему нелинейности голографической записи в общих чертах и,главным образом, в связи с влиянием нелинейности фотоматериала на качество восстановленного изображения. Мы рассмотрим такае ряд особенностей так называемых изображений высшего порядка, которые возникают вследствие нелинейной регистрации голограмм, и приведем некоторые примеры использования изображений высшего порядка для решения практических задач.
Рассмотрим процесс записи голограммы и последующей ее реконструкции для амплитудной голограммы и произвольной характеристики фотоматериала t=f(h).
Пусть волновые функции объектного и референтного излучения определяется в плоскости регистрации голограммы следующими выражениями:
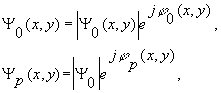 (1) (1)
где |Ψ(x,y)| и φ(х,y) - значения амплитуды и фазы излу-
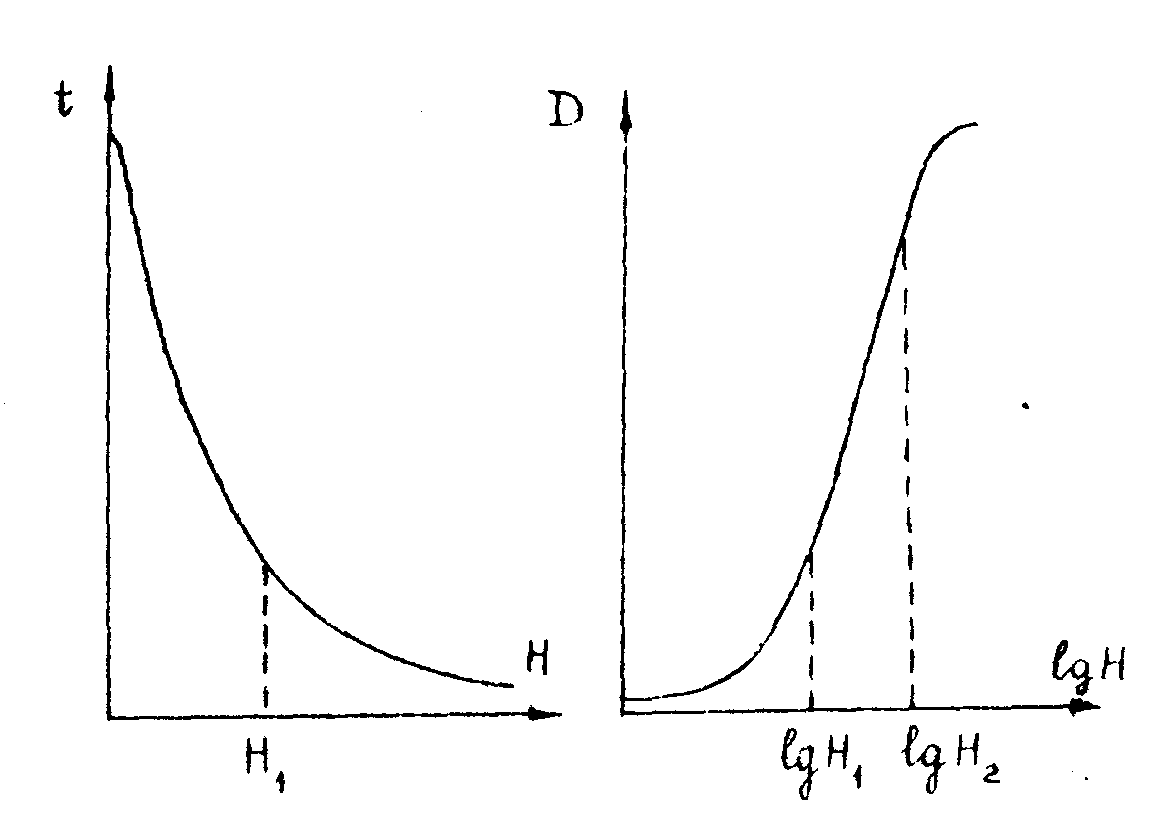
Рис.1. Типичный вид зависимости амплитудной прозрачности фотоматериала от экспозиции t=f(h) и характеристическая кривая d = f(lgh).
чения в некоторой точке с координатами x и y в плоскости голограммы, причем значение амплитуды референтной волны |Ψp| принимается постоянным в пределах области регистрации голограммы.
Распределение интенсивности в плоскости регистрации голограммы можно записать тогда следуюшим образом:
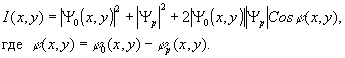 (2) (2)
Рассматривая отдельные слагаемые этого выражения, следует отметить, что |Ψp| 2 характеризует некоторый постоянный уровень интенсивности, создаваемый референтным источником в плоскости регистрации голограммы. Слагаемое |Ψ0(x,y)| 2 характеризует результат взаимной интерференции различных точек объекта и, в случае произвольного объекта, является функцией координат x и у в плоскос-
ти записи голограммы. Как будет показано дальше, зарегистрированный на голограмме результат взаимной интерференции отдельных точек объекта оказывает существенное влияние на качество изображения, восстановленного с помощью нелинейно зарегистрированной голограммы.
Последнее слагаемое в выражении (2) характеризует результат интерференции точек объекта с референтной волной и содержит в себе информацию об амплитуде и фазе объектной волны. Как известно, последующее восстановление объектной волны с помощью голограммы связано с существованием именно этого члена.
Предположим, что распределение интенсивности (2) зарегистрировано на фотоматериале. В общем случае амплитудная прозрачность полученной голограммы является комплексной функцией координат х и у:
t(x,y)=|t(x,y)|e jΘ(x,y), (3)
где |t(x,y)| характеризует изменение амплитуды восстанавливающей волны, а Θ(x,y) - изменение ее фазы при прохождении через голограмму. Будем считать, что голограмма амплитудная и, следовательно, ее прозрачность t(x,y) описывается действительной функцией. Для случая нелинейной регистрации амплитудная прозрачность голограммы, в общем виде, представляет собой некоторую произвольную функцию экспозиции Н:
t(x,y)=g[h(x,y)], (4)
где Н = iτ - экспозиция, а τ - время экспонирования фотослоя при регистрации голограммы.
В дальнейшем, для сокращения записи, мы опустим значки х и y при функциях, описывающих амплитуды и фазы волн. Однако, будем помнить, что не зависит от координат x и у только амплитуда опорной волны.
Подставляя (2) в (4), получим
t=g(h)=g{[|Ψ 0| 2+|Ψp| 2+2|Ψ0||Ψp|cosφ]τ}. (5)
Поскольку φ входит в последнее выражение только под знаком
косинуса, то амплитудная прозрачность голограммы является четной и периодической функцией разности фаз для любой функции g(Н). Следовательно, она может быть представлена в виде ряда Фурье по косинусам упомянутой разности фаз /5/:
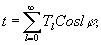 (6) (6)
где Т l - коэффициенты ряда, которые определяются следующим образом:
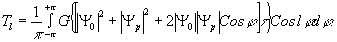 (7) (7)
Найдем значение волновой функции восстановленной голограммой волны в плоскости самой голограммы, для чего умножим волновую функций излучения восстанавливающего источника на амплитудную прозрачность голограммы (6).
Считая, что восстановление голограммы осуществляется с помощью того же источника, который был использован в качестве опорного при ее записи, и разлагая попутно косинус на две сопряженные экспоненты, получим
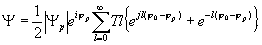 (8) (8)
Выражение (8) характеризует волновое поле, восстановленное нелинейно зарегистрированной голограммой в плоскости самой голограммы. В случае линейной регистрации голограммы выражение для восстановленного голограммой волнового поля описывается следующей функциональной зависимостью:
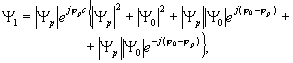 (9) (9)
где постоянная с=с·τ .
Напомним, что первые два члена выражения (9) описывают волну, распространяющуюся вблизи нулевого порядка. Причем, наличие зави-
сящего от координат члена |Ψ0| 2, характеризующего результат взаимной интерференции отдельных точен объекта, приводит к размытию волны нулавого порядка и к образованию так называемого гало.
Третий чл tн выражения (9) описывает волну, распространяющуюся в один из первых порядков дифракции голограммы. Распределение фаз в этой волне в точности совпадает с распределением фаз в объектной пучке, а амплитуда ее пропорциональна амплитуде объектной волны. Таким образом, в одном из первыу порядков дифракции линейно зарегистрированная голограмма восстанавливает неискаженное изображение объекта.
Четвертому члену выражения (9) соответствует так называемое дополнительное изображение, которое является псевдоскопическим.
Возвращаясь к выражению (8), описывающему волновую функцию излучения, восстановленного с помощью нелинейно зарегистрированной голограммы, отметим, что первые три члена атого ряда (с индексами l = 0 и l= 1) во многом напоминают соответствующие члены выражения (9), однако, имеются и принципиальные отличия, которые следует отнести на счет нелинейности фотопроцесса.
В частности, второй член ряда (8), соответствующий l = 1, описывает волну первого порядка, распределение фаз которой в плоскости голограммы в точности совпадает с распределением фаз волны, восстановленной в первом порядке дифракции линейно зарегистрированной голограммы.
Подобная устойчивость фазы волны, зарегистрированной на голограмме, к нелинейным искажениям регистрирующей среды является весьма важным свойством голографической записи и обуславливает возможность восстановления изображения объектов при нелинейной регистрации голограмм.
Амплитуда волны первого порядка, как это следует из выражения (7), зависит от конкретного вида нелинейной характеристики регистрирующей среды g(Н), а также от типа самого объекта (через функцию |Ψ0| ) и положения рабочей точки на характеристике фотоматериала |Ψp| 2 и в общем случае ( произвольного объекта) отличается от амплитуды объектной волны, зарегистрированной на голограмме. Далее мы обсудим этот вопрос подробнее и покажем, какого рода искажения могут возникнуть в изображении вследствие отмеченных выше искаасенкй амплитуды восстановленной с помощью голо-
граммы волны.
Последующие члены ряда с индексами l, равными 2 и выше, характеризуют пространственно разделенные волны, распространяющиеся во второй и выше порядки дифракции голограммы. Эти волны хотя и содержат сведения об амплитуде и фазе зарегистрированной на голограмме волны, однако в искаженном виде, и потому восстанавливают изображение исходного объекта с большими искажениями.
Рассмотрим, к какого рода искажениям в изображении может привести неточное восстановление амплитуды объектной волны в 1 порядке дифракции голограммы. Обратимся к выражению (7) для амплитуды волны, восстановленной в t-том порядке дифракции голограммы. Раскладывая функцию g(Н) в ряд Тэйлора в точке [τ(|Ψ0| 2+ |Ψp| 2], получим для амплитуды волны, восстановленной в 1 порядке дифракции, следующее выражение:
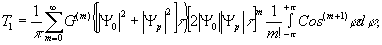 (10) (10)
где g(m){[|Ψ0| 2+|Ψp| 2]τ}- значение производной порядка m функции g(h) при значении аргумента Н , равном [|Ψ0| 2+|Ψp| 2]τ.
Исключим из рассмотрения члены с четными значениями m, поскольку в этом случае интеграл в выражении (10) обращается в 0, для чего используем подстановку m=2n+1, где n = 0, 1, 2,… После интегрирования получим следующее выражение:
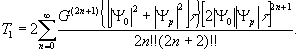 (11) (11)
Для дальнейшего анализа нам необходимо определить конкретный вид характеристики t =g(h). Воспользуемся с этой целью аппроксимацией в виде экспоненциальной зависимости:
g(h)=e -αh, (12)
где α - постоянная.
С учетом ( 12) выражение (11) может быть приведено к следующему виду:
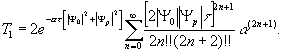 (13) (13)
Используя далее подставленные экспоненты в виде степенного ряда и ограничиваясь тремя членами этого ряда, получим следующее приближенное выражение:
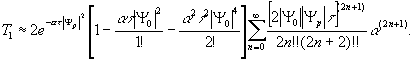 (14) (14)
Напомним, что за исключением амплитуды объектной волны все остальные величины, входящие в последнее выражение, являются постоянными. Поэтому последнее выражение можно представить в следующем виде:
t1 ≈ k1 |Ψ0|+k 2|Ψ0| 3+k 3|Ψ0| 5+… (15)
В самом деле, выражение в квадратных скобках в (14) представляет собой ряд, содержащий |Ψ0| только в четных степенях, при которых стоят постоянные коэффициенты. Сумма, входящая в это же выражение, представляет собой последовательность членов, которые содержат |Ψ0| только в нечетных степенях. Коэффициенты перед членами этой суммы также постоянны. Перемножение двух таких последовательностей приводит к ряду (15), содержащему |Ψ0| только в нечетных степенях.
Представление амплитуды в виде ряда (15) весьма наглядно и позволяет сделать некоторые выводы относительно характера искажений, которые возникают в изображении 1-го порядка при нелинейной регистрации голограммы.
Как видно, первый член этого ряда с точностью до постоянного множителя представляет собой распределение амплитуды объектной волны в плоскости голограммы и с учетом неискаженного восстановления фазы волны в первом порядке дифракция соответствует неискаженному восстановленному изображению объекта. Второй член ряда с учетом правильно восстановленной фазы объектной волны можно предста-
вить в виде произведения волновой функции, соответствующей неискаженной волне обьекта, на множитель |Ψ0| 2. Этот множитель представляет собой не что иное как результат взаимной интерференции различных точек объекта. В линейно зарегистрированной голограмме наличие подобного члена приводит к размытию волны нулевого порядка и к образованию так называемого гало, представляющего собой, в случае диффузного объекта, яркое размытое пятно. В рассматриваемом случае нелинейной записи функция |Ψ0| 2 "размазывает" объектную волну и приводит к образованию фона в изображении. Математически возникновение фона в изображении можно пояснить на примере фурье-голограммы. Для такой голограммы амплитуда поля, восстановленного в ее плоскости, связана преобразованием Фурье с распределением амплитуд в плоскости восстановленного изображения. При этом умножение волновой функции объектной волны на |Ψ0| 2 в плоскости голограммы будет соответствовать операция свертки неискаженного восстановленного изображения с автокорреляционной функцией исходного объекта. Последующие члены ряда (15) характеризуют подобные же свертки, но более высокого порядка.
Чтобы представить характер исказений в изображении, происходящих от присутствия членов, содержащих |Ψ0| в 5-ей и выше степенях в (15), рассмотрим несколько примеров
1. Объект, состоящий из одной точки
В этом случае автокорреляционная функция объекта представляет собой δ-функцию, а неискаженное изображение самого объекта - тоже δ-τункцию. Поэтому свертка автокорреляционной функции объекта с самим объектом есть также δ-функция.
Этот пример подтверждает хорошо известный факт, что в случае точечного объекта нелинейно зарегистрированная голограмма восстанавливает в 1-ом порядке дифракции неискаженное изображение объекта.
2. Объект состоит из нескольких точек
В этом случае автокорреляционная функция объекта представляет собой целый набор δ-функций, причем число δ-функций в автокорреляционной функции превышает число точек в исходном объекте. После свертки идеального изображения объекта с автокорреляцион-
ной функцией самого объекта получим набор δ-функций, причем число δ -функций превышает число точек в исходном объекте, что свидетельствует о появлении ложных изображений. Такого рода ложные изображения исследовали Фризем и Зеленка /6/, а такие Найт /7/. Эти авторы также показали, что если объект состоит из 2 точек, сильно отличающихся по яркости, то вследствие нелинейных искажений голограммы в восстановленном изображении наблюдается эффект "подавления" слабого сигнала сильным, т.е. в восстановленном изображении соотношение яркостей сильной и слабой точек может увеличиться.
3. Произвольный диффузный объект
В этом случае автокорреляционная функция объекта представляет собой весьма протяженную функцию, и в результате свертки этой функции с неискаженным изображением исходного объекта в изображении возникает фон. Таким образом, нелинейная регистрация голограммы диффузного объекта приводит к появлению фона, наложенного на неискаженное изображение. Этот результат также хорошо известен из практики.
Амплитуды волн, восстановленных в высших порядках дифракции, можно рассчитать таким же образом, как это было сделано для волн первого порядка. В частности, для амплитуды волны, восстановленной во втором порядке дифракции голограммы, получим следующее выражение:
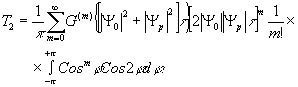 (16) (16)
Предполагая, как и прежде, экспоненциальный ход зависимости амплитудной прозрачности фотоматериала от экспозиции и раскладывая подынтегральную функцию в ряд Тэйлора, можно получить выражение для амплитуды Т 2 в виде ряда:
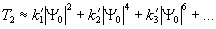 (17) (17)
Как видно, ни один из членов этого ряда не содержит амплитуду объектной волны в первой степени, что свидетельствует о сильных искажениях амплитуды объектной волны. Фаза объектной волны, как уже
отмечалось выше, также искажается, поскольку в порядке дифракции с номером l она усиливается в l раз. Таким образом, в случае произвольного объекта в высших порядках дифракции голограммы вместо изображения объекта образуется сильно размытая картина.
Моино также показать, что ни один из амплитудных коэффициентов tl (начиная с l = 2) не будет содержать модуль амплитуды объектной волны ни в 0, ни в 1 степени. Вернемся к выражению (10) и запишем его для случая амплитуды волны порядка l:
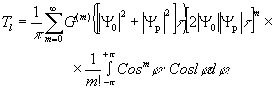 (18) (18)
В случае m =
0 интеграл в (18) имеет вид: 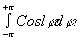 В силу четности косинуса этот интеграл
равен 0 при любом значении
и, следовательно, ни в одном из порядков l
не содержится |Ψ0|
в нулевой степени, т.е. нет постоянных коэффициентов в выражениях для tl.
В силу четности косинуса этот интеграл
равен 0 при любом значении
и, следовательно, ни в одном из порядков l
не содержится |Ψ0|
в нулевой степени, т.е. нет постоянных коэффициентов в выражениях для tl.
При m = 1 интегрирование в (18) дает следующий результат:
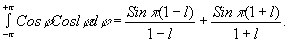 (19) (19)
Как следует из (19), второй член равен 0 для любого целого значения l. Первый член (19) также обращается в 0 при целых l за исключением l =1, когда
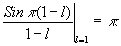 (20) (20)
Таким образом, только амплитудный коэффициент Т 1, соответствующий первому порядку дифракции, содержит |Ψ0| в первой степени. Все остальные коэффициенты Тl могут содержать |Ψ0| только во второй и выше степенях. Можно сослаться на результаты исследований, выполненных различными авторами, которым удалось для случая диффузного объекта восстановить изображения лишь в 1-ом порядке дифракции нелинейно зарегистрированной голограммы. Во втором и третьем порядках вместо изображения объекта восстанавливались лишь размытые пятна.
Тем не менее, восстановление изображений объектов в высших порядках дифракции все же оказывается возможным в некоторых случаях.
Так, например, для объекта, состоящего из одной точки, амплитуда объектной волны приблизительно постоянна и плоскости записи голограммы и информация об объекта заключена в распределении фаз объектной волны. При этом, во второй порядке дифракции амплитуда волны, восстановленной голограммой, постоянна, как следует из (17) а фаза - равна удвоенной фазе объектной волны. Можно показать,что в результате умножения фазы сферической волны на некоторое число l плоскость сфокусированного изображения точки приближается к плоскости голограммы в l раз, и, кроме того, в восстановленном изображении возникают аберрации /8/ которые, однако, по крайней мере в ближних порядках, на сильно размывают восстановленное изображение точки.
Восстановление изображений в высших порядках возможно но только для точечного объекта: основное условие, которое должно быть выполнено при этом - постоянство амплитуды объектной волны в плоскости записи голограммы. Такому условию, например, удовлетворяют прозрачные объекты со слабо изменяющимся показателей преломления. В литературе также имеются сведения о восстановлении во 2-ом и 3-ем порядках дифракции изображении объектов типа транспарантов с изображениями букв алфавита, фрагментов текста и т.п., при освещении объектов на просвет направленный пучком света /9-11/.
Возможность восстановления изображений в этом случае объясняется тем, что для объекта с достаточно грубыми деталями в плоскости регистрации голограммы образуется теневая проекция этого объекта (см.рис.2-а), которая и регистрируется на голограмме. По существу, на такой голограмме регистрируется результат интерференции опорной волны со сферической (или плоской) объектной волной в пределах тех участков голограммы, которые не затеняются непрозрачными частями объекта. Будучи зарегистрирована на нелинейном материале, такая голограмма восстанавливает изображение точечного источника в высших порядках дифракции. При этом, сечения восстановленных в высших порядках дифракции голограммы пучков будут подобны теневой проекции исходного объекта (рис.2б) и сохранят достаточную четкость,
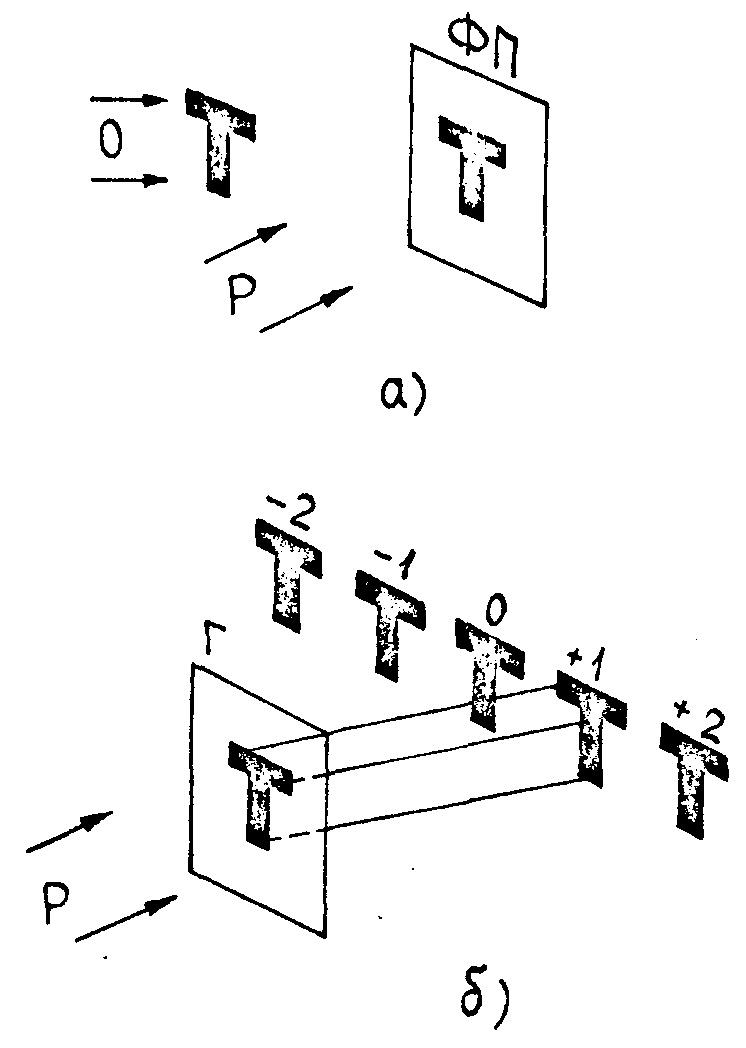
Рис.2.
Иллюстрация возможности восстановления изображений высшего порядка с грубыми деталями:
а) регистрация голограммы;
б) восстановление изображений.
которая, однако, будет падать по мере удаления от голограммы. Фактически наблюдаемые в подобной ситуации в различных порядках дифракции картины не являются изображениями в том смысле, в котором это понятие употребляется в оптике, а представляют собой теневые проекции исходного объекта.
Одной из разновидностей нелинейной голографической записи являются фазовые голограммы. Основные проявления нелинейности записи в этом случае выражаются также как и в рассмотренном только что случае амплитудных голограмм в возникновении высших порядков дифракции на голограмме и в искажении изображений первого порядка /12-14/.
Причем, как и в амплитудной голограмме, основным источником шума в восстановленном изображении является взаимная интерференция различных точек объекта в процессе записи голограммы. Мы не
будем здесь подробно анализировать этот случай. Отметим только, что уровень фона в изображениях, восстановленных с помощью разовых голограмм, зачетно сильней, чем для амплитудных голограмм.
После рассмотрения основных эффектов, связанных с нелинейной регистрацией голограмм, естественно обсудить 2 следующих вопроса:
1. Можно ли уменьшить искажении, возникающие в восстановленном изображении вследствие нелинейной регистрации голограмм, и каким образом?
2. Следует ли рассматривать нелинейность регистрирующей среды только как нежелательный фактор, приводящий лишь к искажениям в восстановленной изображении, и нельзя ли извлечь какие-либо "положительные" эффекты, используя нелинейную запись голограммы?
Рассматривая пути уменьшения нелинейных искажений, следует прежде всего перечислить такие возможности, как выбор рабочей точки на характеристике фотоматериала, выбор соотношения интенсивностей объектного и референтного пучков, режим обработки фотоматериала. В целом, вопрос о получении максимально допустимой яркости изображения при заданном уровне нелинейных искажений относится к проблеме так называемой оптимизации голограммы и решается с учетом реальной характеристики материала, характера конкретного объекта и условий регистрации голограммы (т.е. положения рабочей точки на характеристике фотоматериала, отношения интенсивностей объектного и референтного пучков и т.д.) /15,16/.
Некоторые дополнительные возможности компенсации фона, обусловленного нелинейной регистрацией голограмм, могут быть реализованы в случае фазовой голографической записи.
Как известно, при регистрации фазовых голограмм распределение интенсивности экспонирующего излучения преобразуется в изменения показателя преломления и в изменения толщины голограммы. Причем, изменения толщины оказывают существенное влияние главным образом в области относительно низкиг пространственных частот записи - до 100 лин/мм /17/ и быстро спадают до нуля при более высоких пространственных частотах. Если учесть, что в большинстве практических случаев несущая пространственная частота записи составляет несколько сотен лин/мм, то становятся понятным, что результат интерференции различных точек объекта с опорным пучком регистрируется на го-
логранме только в виде изменений показателя преломления. Взаимная интерференция точек объекта регистрируется как в виде изменений показателя преломления, так и в виде изменений толщины голограммы.
В силу нелинейности записи голограммы зарегистрированный на ней результат взаимной интерференции различных точек объекта приводит, как уже отмечалось, к возникновению фона в изображении. Однако, в фазовой голограмме этот фон может быть частично подавлен, если поместить такую голограмму в иммерсионную среду. При этом рельеф на поверхности голограммы окажется скомпенсированным /18,19/. Существенно отметить, что яркость изображения при этом не уменьшится, поскольку иммерсия не влияет на результат интерференции точек объекта с опорной волной, представленный на голограмме в виде изменений показателя преломления.
Используя подобный метод, модно уменьшить уровень фона в восстановленном изображении почти в 2 раза. Естественно, что при рассмотренном методе компенсации подавляется только та часть фона, которая обусловлена наличием рельефа на поверхности голограммы. Остальная часть фона, связанная с изменениями показателя преломления голограммы, вследствие взаимной интерференции различных точек объекта остается. Однако оказывается, что и эта часть фона может быть частично подавлена, если применить так называемое реверсивное отбеливание, предложенное и исследованное Ламбертсом и Куртцем /20/.
В отличие от обычного процесса отбеливания, при котором голограмма отбеливается после фиксирования, при реверсивном отбеливании голограмма отбеливается после проявления. Таким способом можно устранить рельефную составляющую голограммы и даже образовать на ней рельеф обратного знака по отношению к рельефу, который образуется при обычном отбеливании. То есть в тех местах, где при обычном отбеливании образуются "микробугорки", при реверсивном отбеливании образуются "микровпадинки". При этом можно частично скомпенсировать изменения показателя преломления, обусловленные взаимной интерференцией точек объекта, и тем самым еще больше снизить нежелательный фон в восстановленном изображении.
До сих пор мы рассматривали нелинейную запись голограмм в основном с точки зрения искажений, которые она вносит в восстановленные изображения. Однако, используя нелинейность фотоматериала, в
некоторых случаях удается извлечь и определенную выгоду из нелинейности фотопроцесса. Проиллюстрируем это двумя примерами из голографической интерферометрии.
Первый пример касается вопроса о повышении чувствительности голографического интерферометра за счет использования высших порядков дифракции нелинейно зарегистрированной голограммы. При этом используется то свойство голограммы, что в l-ом порядке дифракции она восстанавливает волну, фаза которой усилена в l раз по сравнению с исходной объектной волной, зарегистрированной на голограмме. В частности, как показали К.С.Мустафин, В.А.Селезнев, Е.И.Штырков /21/,
используя наложение сопряженных волн порядка l, можно увеличить чувствительность голографического интерферометра в 2l раз по сравнению с обычным интерферометром.
Процесс образования подобной интерферограммы можно рассмотреть на следующем простом примере. Пусть на фотопластинку, на которой регистрируется голограмма, падают 2 плоские волны под некоторым углом α (см. рис.3), и в одну из них помещен исследуемый объекта например, фазовая неоднородность.
Зарегистрировав голограмму на нелинейном участке кривой фотоматериала, осветим ее двумя параллельными пучками лучей: i и ii на рис.3. Причем, углы паления этих пучков на голограмму подберем таким образом, чтобы восстановленная пучком i волна + l порядка распространялась в одном направлении с волной - l порядка, восстановленной пучком ii. Поскольку обе восстановленные волны имеют взаимно сопряженные волновые фронты, в каждой из которых фаза объектной волны усилена в l раз, то суммарные изменения фазы оказываются усиленными в 2l раз, что как раз и свидетельствует о повышении чувствительности интерферометра в 2l раз.
Однако необходимо отметить, что этот метод может быть применен для объектов, которые вносят слабые искажения в фазу проходящей волны, такие, чтобы амплитуда объектной волны оставалась приблизительно постоянной в пределах регистрируемой голограммы. В противном случае нелинейность записи приведет к искажениям интерферограммы. Кроме того, искажения интерферограммы возникают и при совмещении объектных волн + l и -l порядка, поскольку такое совмещение достигается за счет разворота опорного пучка /22/.
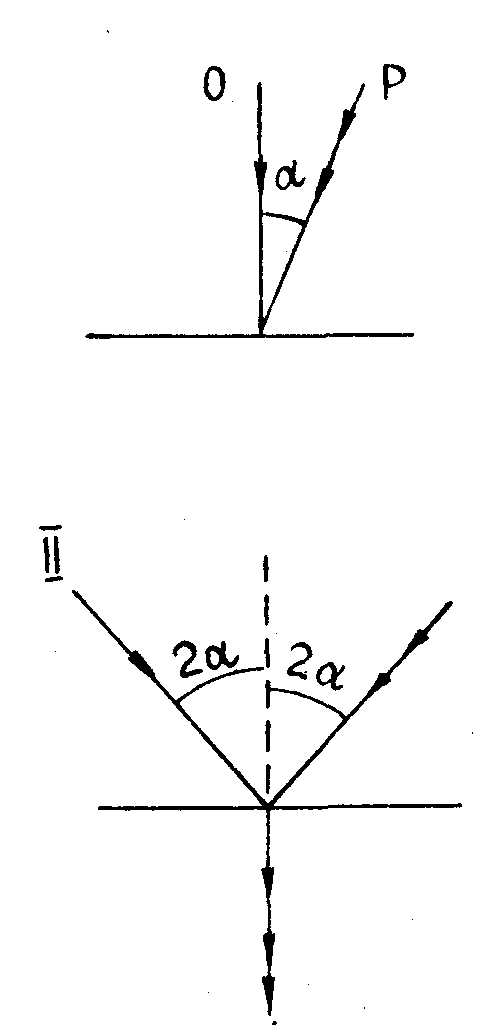
Рис.3.
Схема регистрации голограммы и получения интерферограмм с использованием высших порядков дифракции.
В качестве другого примера удачного использования высших порядков дифракции нелинейно зарегистрированной голограммы рассмотрим двухдлинноволновый метод изучения дисперсионных свойств фазовых объектов, предложенный Г. В. Островской и Ю. И. Островским /23/.
Суть этого метода состоит в том, что на одной фотопластинке либо одновременно, либо последовательно во времени регистрируются 2 голограммы одного и того же фазового объекта на двух длинах волн, отличающихся в 2 раза. Причем, пути прохождения пучков для обеих длин волн и углы их падения на фотопластинку одинаковы за исключением отличий, обусловленных дисперсией объекта. В результате на фотопластинке регистрируются 2 голограммы, несущие пространственные частоты которых отличаются в 2 раза. Поэтому, при реконструкции таких голограмм с помощью одной из двух длин волн, используемых при записи, происходит наложение волны, восстановленной в 1-ом порядке одной голограммы с волной, восстановленной во
втором порядке другой голограммы. Отличия в 2-х наложенных волнах, как показали авторы, обусловлены только дисперсией объекта, а поэтому полученная таким способом интерферограмма характеризует дисперсионные свойства объектов. Следует, однако, помнить, что подобный метод, как и рассмотренный паред ним, пригоден для изучения объектов лишь с малыми градиентами показателя преломления.
Л и т е р а т у р а
1. d.gabor. Рrос.roy.soc.(london), a197, 454, 1949.
2. e.w.leith, j.upatnieks. josa, 52, 1123, 1962.
3. e.n.leith, j.upatnieks. josa, 54, 1295, 1964.
4. e.n.leith, j.upatnieks. josa, 53, 1377, 1963.
5. j.m.j.tokarski. appl.optics, 7, 989, 1968.
6. a.a.frisem, j.s.zelemka. appl.opt., 6, 1755, 1967.
7. g.r.knight, appl.opt., 7, 205, 1968.
8. b.pawluczyk. optica acta, 19, 291, 1972.
9. j.c.viénot, p.smiegielski, h.royer. "holographie optique developpements applications." dunod, paris, 61, 1971.
10. o.brynngdahl, a.lohmann. josa, 58, 1325, 1968.
11. А.П.Комар, М.В.Стабников, Б.Г.Турухано. ДАН СССР, 169, 1052, 1966.
12. j.upatnieks, c.leonard. josa, 60, 297, 1970.
13. g.h.f.velsel. opt.commun., 3, 133,, 1971.
14. h.damman. josa, 60, 1635, 1970.
15. И.С.Барбанель, Э.И.Крупицкий. "Опт. и спектроск.", 33, 1145, 1972.
16. И.С.Барбанель, Э.И.Крупицкий. "Оптика и спектроскопия"(в печати).
17. h.m.smith, josa, 58, 533, 1968.
18. j.upatnieks, c.leonard. josa, 60, 297, 1970.
19. b.l.lamberts, c.n.kurtz, c.d.edgett. josa, 59, 1544a.1969.
20. r.l.lamberts, c.n.kurtz. appl.opt., 10, 1342, 1971.
21. К.С.Мустафин, В.А.Селезнев, Е.И.Штырков. "Опт. и спектр, 28, 1186, 1970.
22. r.w.meier. josa, 55, 987, 1965.
23. Г.В. Островская, Ю.И.Островский. ЖТФ, 40, 2419, 1970.
Дополнительная литература
24. a.kozma. photographic recording of spatially modulated coherent light. josa, 56, 428, 1966.
25. g.w.goodittan, g.r.knight. effects of film nonlinearities on wavefront reconstruction images of diffuse objects. josa, 58, 1276, 1968.
26. w.h.lee, m.o.greer. noise characteristics of photographic emulsions used for holography. josa, 61, 402, 1971.
27. f.g.kaspar, r.l.lamberts. effects of some photographic characteristics on the light flux in a holographic Image. josa, 58, 970, 1968.
28. j.c.wyant, m.p.givens. effect of the photographic gamma on the luminance of hologram reconstructions. appl.opt., 9, 810, 1970.
29. d.j.de bitetto, a.l.dalisa. elimination of flare light in hologram recording of diffuse objects. appl.opt., 10, 2292, 1971.
30. a.kozma, g.w.jull, К.o.hill. an analytical and experimental study of nonlinearities in hologram recording. appl.opt., 9, 721, 1970.
31. j.upatnieks, c.d.leonard. linear wavefront reconstruction from nonlinearly recorded holograms. appl.opt., 10, 2365, 1971.
32. o.bryngdhall, a.w.lohmann. interferograms are Image holograms. josa, 58, 141, 1968.
33. h.j.gerritsen. nonlinear effects in Image formation. appl.phys. lett., 10, 239, 1967.
3 4. Ю.Н.Денисюк, Г.Б.Семенов, Н.А.Савостьяненко."О влиянии нелинейности фотоматериала на характеристики амплитудных голограмм. Опт. и спектр., 29, 994, 1970.
35. В.Н.Славинская "Пространственная фильтрация структуры голографического изображения как результат нелинейных искажений при записи голограммы". Опт. и спектр., 31, 1145, 1972.
36. j.a.jemey, nonlinearities of photopolymer holographic recording materials. appl.opt., 11, 1371, 1972.
37. j.p.prenel. sbudy of the linearity of response of holographic photosensitive emulsion. opt. and laser technol., 3, 157, 1971.
38. Г.В.Островская. "Нелинейные эффекты в голографии". Материалы . iv Всесоюзной школы по голографии, 1973 ( в печати).
39. С.s.vicram, r.s.sirohi. a new method for linear recording in holography. opt.acta, 19, 39, 1972.
40. yu f.Т.s. experiment in linear optimization of the holographic process. appl.opt., 11, 949, 1972.
41. c.clauseu, h.dammann. effects of intrinsic nonlinearities on efficiency and Image contrast of bleached holograms. opt.commun., 2, 263, 1970.
42. М.К.Мустафин, В.А.Селезнёв. "Об аберрациях в голографической интерферометрии при использовании высших порядков дифракции". Опт. и спектр., 29, 990, 1970.
43. c.j.palermo, e.n.leith, r.o.harger, w.a.loucka. suppression of the holographic twin Image by nonlinear techniques. appl.opt., 9, 2813, 1970.
44. Дж.Гудмен."Введение в фурье-оптику", Мир, Москва, 1970.
45. yu f.t.s. five point analysis of nonlinear holograms. josa, 59, 360, 1969.
46. r.j.collier, c.b.burckhardt, l.h.lin. optical holography. acad. press, n.y. and london, p.337, 1971.
47. m.marquet. performances en holographic. rev.opt., 45, 404, 1966.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

