|
|
 |
 |

|
| |
ДИФРАКЦИОННАЯ ЭФФЕКТИВНОСТЬ И ОТНОШЕНИЕ СИГНАЛА К ШУМУ ФАЗОВЫХ ГОЛОГРАММ ДИФФУЗНЫХ ОБЪЕКТОВ
В.И.Локшин, Г.Б.Семенов
Проведен теоретический анализ и представлены экспериментальные значения дифракционной эффективности и отношения сигнал к шуму фазовых голограмм диффузных объектов.
Существенным достоинством фазовых голограмм, обуславливающим широкое их применение при решении ряда практических задач, является высокая дифракционная эффективность при достаточно высоком отношении сигнал/шум в восстановленном изображении. Как известно, теоретический предел дифракционной эффективности для двумерной синусоидальной фазовой решетки составляет 35,9%, а для бинарной фазовой решетки - 40,6%. Однако, для широко распространенного случая диффузных объектов не удается получить столь высокое значение дифракционной эффективности. Кроне того, восстановленное с помощью фазовых голограмм изображение таких объектов характеризуется, по сравнению с регулярными фазовыми решетками, повышенным уровнем шумов. Рядом авторов было показано, что перечисленные особенности фазовых голограмм диффузных объектов связаны со случайным характером распределения поля объекта в плоскости регистрации голограмм, Настоящий доклад основан на результатах исследований, проведенных Упатниексом, Леонардом и Вельзелем /1,2/ и посвящен анализу дифракционной эффективности и отношения сигнал/шум фазовых голограмм диффузных объектов.
Предположим, что фазовая голограмма получена путем отбеливания амплитудной голограммы, зарегистрированной по обычной двухлучевой схеме. Рассмотрим дифракционную аффективное двумерной фазовой голограммы диффузного объекта.
Пусть волновое поле излучения, рассеянного диффузным объектом
- 314 -
в плоскости регистрации голограммы, имеет вид;
y
o(x,y) = Ao(x,y)exp[jj
o(x,y)] (1)
где Ao(x,y) и j
o(x,y) случайные величины, характеризующие значение амплитуды и фазы объектной волны для произвольной точки с координатами x,y в плоскости фотопластинки Распределение волнового поля излучения референтного источника в той же плоскости может быть представлено аналогичным образом:
y
r(x,y) = Ar∙exp[jj
r(x,y)] (2)
где Ar и j
r(x,y) - амплитуда и фаза референтной волны. Причем, Ar предполагается постоянной в пределах голограммы.
На фотопластинке регистрируется результат интерференции волновых фронтов j
o(x,y) и Ar(x,y). Соответствующее распределение интенсивности излучения можно записать следующим образом:
I(x,y) = (y
o+y
r)•(y
*o+y
*r) =
= А2o(x,y)+A 2r+2A rA o(x,y)Cos j
(x,y) (3)
Где j
(x,y) = j
o(x,y) - j
r(x,y)
Для получения фазовой голограммы распределение интенсивности (3) регистрируется на фотопластинке, которая после проявления и фиксирования подвергается процессу отбеливания. При этом металлическое серебро преобразуется в нерастворимые соли серебра, прозрачные для видимой области спектра. Предположим, что приращение оптической толщины фазовой голограммы пропорционально величине экспозиции, вызвавшей это приращение. Тогда амплитудную прозрачность голограммы можно записать в следующем виде:
Ta
(x,y) = exp[j∙kBtI(x,y)] (4)
где В - тангенс угла наклона зависимости приращения оптической
- 315 -
толщины фазовой голограммы от величины экспозиции, а t – время экспозиции, а 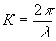 - волновое число. - волновое число.
Подставляя (3) в (4), получим:
Ta
(x,y) = exp[jkBt{ А2o(x,y)+A 2r} ´
´
exp[jkBt2ArAo(x,y)Cosj
(x,y)] (5)
Разложим второй сомножитель в выражении (5) в ряд Фурье по косинусам разностей фаз (х,у). Тогда выражение (5) примет вид:
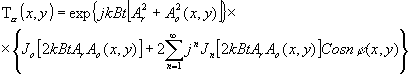 (6) (6)
где Jo и Jn - Функции Бесселя 1-го рода нулевого порядка и порядка n, соответственно.
Пусть реконструкция голограммы осуществляется с помощью референтного источника (2). Тогда, умножая (2) на амплитудную прозрачность голограммы (6), получим волновую функцию излучения, восстановленного голограммой. В соответствии с разложением (6) эта волновая функция характеризует набор волн, распространяющихся в различные порядки дифракции голограммы. Амплитуда волны, распространяющейся в порядок дифракции n определяется выражением:
An = ArJn[2kBtArAo(x,y)] (7)
В рассматриваемом случае диффузного объекта, когда амплитуда и фаза объектной волны в плоскости голограммы меняется случайным образом от точки к точке, амплитуда восстановленной волны An также будет меняться случайно от точки к точке. Поэтому дифракционную эффективность голограммы можно записать в таком виде:
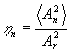 (8) (8)
где <A2n> - усредненное по поверхности голограммы значение
- 316 -
интенсивности излучения, дифрагированного в n порядок.
Используя теорему о математическом ожидании /4/, среднее значение интенсивности с учетом (7) можно записать следующий образом:
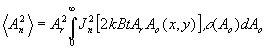 (9) (9)
где r
(Ao) - функция распределения плотности вероятности амплитуды объектной волны Ao в плоскости записи голограммы. Для определения функции распределения r
(Ao) воспользуемся моделью диффузного объекта, при которой сам объект заменяется набором точечных источников со случайными фазами излучения /1/. В этом случае функция плотности вероятности амплитуды будет иметь вид распределения Релея:
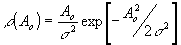 (10) (10)
где s
2 - дисперсия случайной амплитуды объектной волны Ao. Подставляя (10) в (9) и интегрируя, получим:
<A2n> = A2rexp[-(2kBtArs
)2]In[(2kBtArs
)2] (11)
где In[-(2kBtArs
)2] - модифицированная функция Бесселя первого рода порядка n.
Используя (8), получим следующее выражение для дифракционной эффективности голограммы по отношению к порядку дифракции n:
h
n = exp[-(2kBtArs
)2]In[(2kBtArs
)2] (12)
Из (12) можно получить, в частности, выражение для дифракционной эффективности голограммы для первого порядка дифракции:
h
1 = exp[-y2]I1(y2) (13)
- 317 -
где y=2kBtArs
.
Анализ этого выражения показывает, что максимальная дифракционная эффективность фазовой голограммы диффузного объекта равна 22. Ход зависимости h
1= ¦
(y 2) представлен на рис.1.
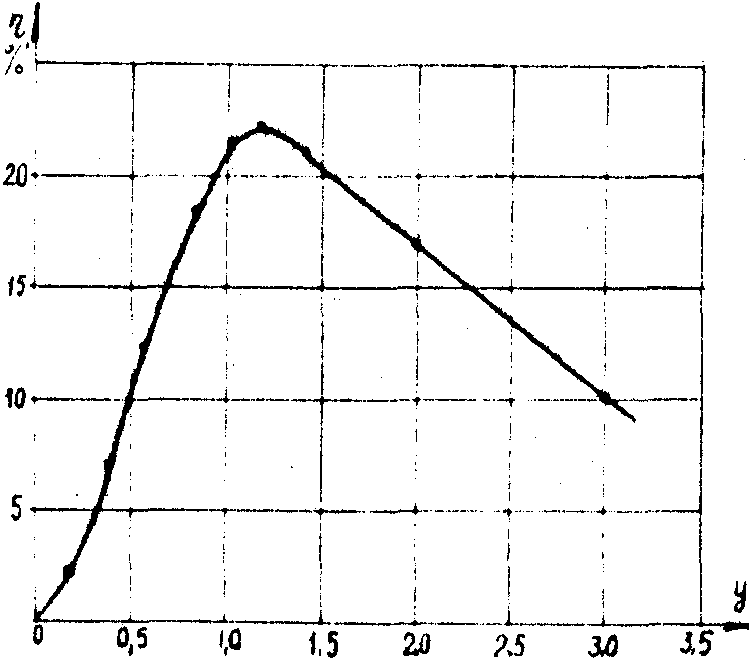
Рис.1. Зависимость дифракционной эффективности h
1 от y2
Другой важной характеристикой изображения является отношение сигнал/шум. Для анализа этого параметра необходимо знать волновую функцию излучения, распространяющегося в первом порядке дифракции. Для нахождения этой функции умножим амплитудную прозрачность голограммы (6) на волновую функцию референтного источника (2) и выделим слагаемые, соответствующие n=1.
С точностью до постоянного множителя получим:
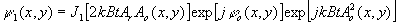 (14) (14)
Для последующего анализа удобно представить сомножитель exp[jkBtA2o(x,y)], а также функцию Бесселя J1[2kBtArAo]
- 318 -
в виде степенных рядов относительно аргументов Функции Бесселя и экспоненциальной функции, соответственно. Ограничиваясь членами рядов, содержащими указанные аргументы в первой степени, получим;
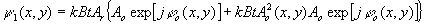 (15) (15)
Первое слагаемое в фигурных скобках представляет собой восстановленное голограммой волновое поле излучения объекта. Это излучение, распространяясь за голограммой, образует неискаженное изображение объекта. Второе слагаемое также содержит волновое поле излучения объекта, которое, однако, умножается на случайную функцию координат Х и У - A2o(x,y), Присутствие этого множители обуславливает искажения волнового фронта, что приводит, в свою. очередь, к возникновению шумов в изображении. Из предыдущего анализа следует, что возникновение функции A2o(x,y) связано с наличием интерференции между различными точками объекта. При регистрации голограммы диффузного объекта, интенсивность света в интерференционной картине меняется случайным образом от точки к точке в плоскости регистрации. В фазовой голограмме подобные колебания интенсивности отображаются как в виде изменений показателя преломления, так и в виде соответствующего изменения рельефа. При восстановлении такой голограммы часть реконструирующего излучения идет на формирование изображения, а часть света рассеивается фазовыми неоднородностями, создавая фон в изображении.
Определим параметр сигнал/шум как отношение усредненной по площади голограммы величине потока излучения, образующего изображение объекта, к средней величине рассеянного потока. Этот параметр можно выразить также и через пропорциональные упомянутым потокам усредненные интенсивности. Принимая во внимание (15), получим:
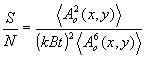 (16) (16)
При вычислении усредненных величин в числителе и знаменателе выражения (16) сохраним принятое ранее предположение о релеевском
- 319 -
характере распределения амплитуды объектной волны в плоскости записи голограммы (10). Тогда, после вычисления соответствующих интегралов, аналогичных (9), получим:
<A2o(x,y)> = 2s
2 (17a)
<A6o(x,y)> = 48s
6 (17б)
где s
2 - дисперсия амплитуды объектной волны в плоскости регистрации голограммы. Подставляя (17а) и (17б) в (16), получим:
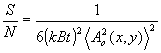 (18) (18)
Преобразуем выражение (18), введя в него такие параметры, как величину отношения интенсивностей референтной волны к объектной - М и среднюю величину экспозиции при записи голограммы – Н:
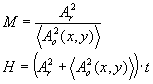 (19) (19)
где t - время экспозиции.
Тогда выражение (18) можно привести к следующему виду:
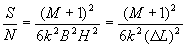 (20) (20)
Как следует из (20), отношение сигнал/шум растет при увеличении отношения интенсивностей референтного и объектного пучков. Однако, увеличение этого отношения приводит к снижению дифракционной эффективности и, следовательно, к уменьшению яркости восстановленного изображения.
Как отмечалось ранее, распределение интенсивности экспонирующего излучения преобразуется в фазовой голограмме в соответствующее
- 320 -
изменение показателя преломления и толщины эмульсии. Причем, изменение толщины эмульсии проявляется в относительно узком интервале пространственных частот голографической записи. (По данным, приведенный в работе Ламбертса /5/ до 200 лин/мм). Поэтому при регистрации голограммы с высокочастотной несущей пространственной частотой, т.е. с большими углами между объектным и референтным пучками, изменение толщины оказывается обусловленным только интерференцией точек объекта между собой. Интерференция точек объекта с опорной волной главным образок определяет изменение показателя преломления. Отсюда следует возможность увеличения отношения S/N для фазовых голограмм: величина этого параметра растет, если поместить голограмму при реконструкции в иммерсионную среду.
Для иллюстрации приведем некоторые данные для дифракционной эффективности и отношения S/N, фазовых голограмм диффузных объектов, полученных нами на Микрате ВР-Л с последующим отбеливанием в красной кровяной соли. В качестве объекта было использовано матовое стекло.
На рис.2 приведена зависимость дифракционной эффективности от средней плотности голограммы D до отбеливания. Отметим, что максимальная величина составила 10% и соответствует средней плотности D около 0,8.
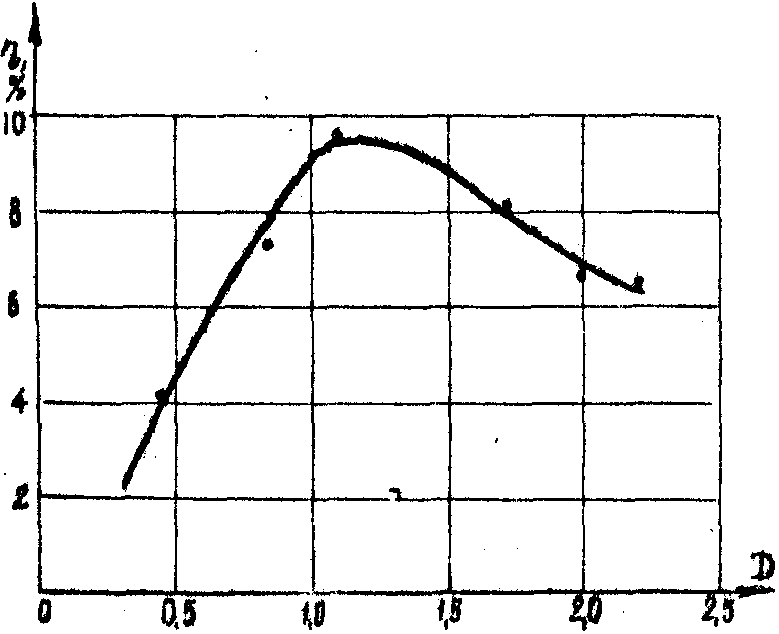
Рис.2. Зависимость дифракционной эффективности от средней плотности голограммы D до отбеливания.
- 321 -
На рис.3 изображены зависимости S/N аналогичных голограмм в зависимости от того же параметра D для 2-х случаев:
а) без помещения голограммы в иммерсионную среду;
б) с использованием иммерсии.
Сравнение этих кривых позволяет сделать вывод об эффективности использования иммерсии.
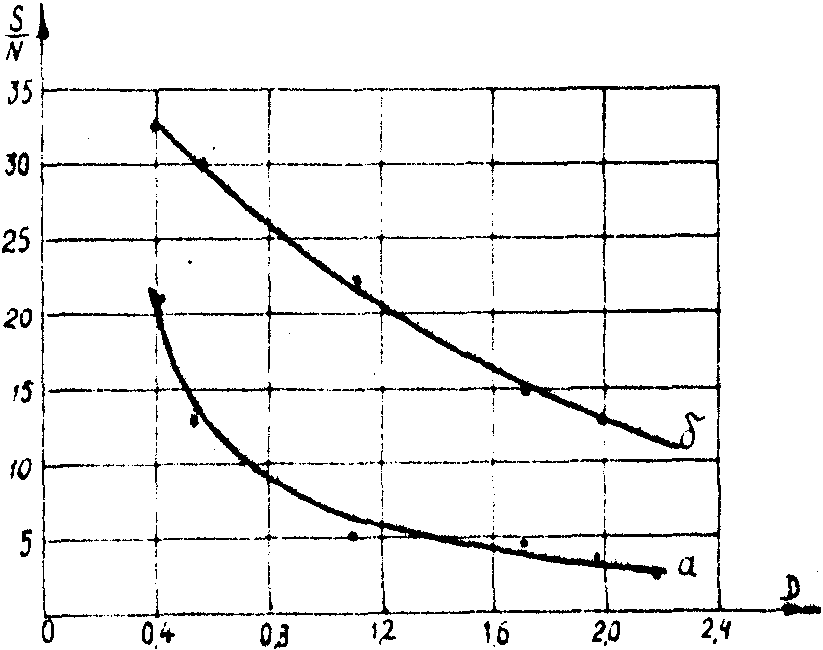
Рис.5. Зависимость S/N от средней плотности голограммы D:
а - голограмма без иммерсионной среды;
б - голограмма с иммерсией.
- 322-
Литература
1. I.Upatnieks and C.Leonard. J.Opt.Soc.Am., 60, 297, Я970.
2. C.H.F.Velzel. Opt.Comnmn., v.3, N 3, р.р. 135-136, 1971.
3. Дж.Гудмен. Введение в Фурье-оптику, изд. "Мир", Москва, стр.305, 1970.
4. Е.С.Вентцель. Теория вероятностей, изд. "Наука", Москва, стр.212, 1964.
5. R.L.Lamberts and C.N.Kurtz. Appl.Opt. 10, 6, р.р.1342-1347, 1971.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

