|
|
 |
 |

|
| |
АХУСТООПТИЧЕСКАЯ ГОЛОГРАФИЯ
В.И.Телешевский
Акустооптическая голография объединяет методы получения изображения акустических полей и расположенных в них объектов на основе непосредственного взаимодействия света со звуком. Акустическое поле за рассеивающий объектом представляется как фазовая оптическая голограмма объекта, дифракция света на этом поле как процесс восстановления изображения. Рассматриваются изображающие свойства акустооптического взаимодействия, дифракционные методы визуализации акустических полей и объектов, а такие использование этих методов для оптического исследования акустических полей. Приводятся теоретические и экспериментальные результаты.
Введение
Любой процесс записи акустической голограммы (звуковой, ультразвуковой) и восстановления изображения можно рассматривать как определенное акустооптическое преобразование, обеспечивающее полную или частичную визуализацию поля источника звука. К настоящему времени известен ряд акустооптических преобразований, подробно рассмотренных в монографиях /1-5/ и обзорах /6-8/. Преобразования в акустической голографии сводятся к трем основным методам:
1) запись акустической голограммы в нелинейной регистрирующей среде в поле интерференции предметной и опорной волн с последующим оптическим восстановлением;
2) синтез акустической голограммы сканированием поля предметной волны с последующим оптическим восстановлением;
3) визуализация на основе непосредственного взаимодействия
- 287 -
света с акустическим полем.
Первый метод является акустическим аналогом классической схемы оптической голографии с опорным пучком и целиком определяется свойствами регистрирующей среды. Второй метод использует известную возможность непосредственной регистрации фазы акустических полей и электрическую имитацию опорной волны. Однако в каждом из этих методов процессы записи акустической голограммы и оптического восстановления разнесены во времени к пространстве. Очевидно, что полное совмещение этих процессов возможно при непосредственном взаимодействии света с исследуемым акустическим полем. Методы, основанные на таком взаимодействии, составляют, по существу, отдельное направление в акустической голографии. Это направление, исходя из его физической природы, целесообразно назвать акустооптической голографией .
Голография в волнах любой физической природы базируется на фундаментальном свойстве рассеянных волновых полей сохранять информацию о расположенных в них объектах /9,10/. Основным вопросом голографии является выбор способа регистрации рассеянного поля в виде оптической периодической структуры (плоской или объемной), дифракция света на которой приводит к восстановлению изображения. В оптической голографии такая структура записывается интерференционным способом в нелинейной регистрирующей среде добавлением к рассеянной волне когерентной ей опорной.
Однако свойствами оптической периодической структуры обладают и акустические поля. Акустические поля объемных или поверхностных волн вызывают в оптически прозрачных средах или на границах раздела сред периодические распределения различных физических свойств, в том числе и оптических; показателя преломления, коэффициента двулучепреломления, смещений поверхности и других /11/. Акустическое поле модулирует практически все параметры световой волны: амплитуду, интенсивность, фазу, частоту, поляризацию /12/ . В результате необходимая информация об акустическом поле переносится в световое и может быть выделена как непосредственно, так и с применением оптической обработки и фильтрации. Таким образом, акустическая голография охватывает широкий круг вопросов модуляции света звуком, актуальных для ряда областей науки и техники: дефектоскопии и интроскопии с целью выявления внутренней структуры
- 288 -
или дефектов объектов, при оптическом модулировании волновых процессов, в оптическом исследовании акустических полей, в оптической обработке информации, метрологии, в оптической голографии и интерферометрии.
1. Дифракция свата на акустическом поле как метод голографии
Акустическое поле за рассеивающим объектом, облучаемым монохроматической звуковой волной, представляет собой результат интерференции падающей и рассеянной волн. С оптической точки зрения такое поле представляет собой фазовый периодический объект, обладающий свойствами голограммы. Очевидно, что дифракция света на этом поле должна привести к появлению изображения объекта в дифракционных порядках. Следовательно, акустическое поле за рассеивающим объектом можно рассматривать как акустическую голограмму (типа голограммы Габора) этого объекта, а дифракцию света на поле - как процесс восстановления изображения. Это свойство лежит в основе акустооптической голографии и справедливо для любых типов акустических волн: объемных или поверхностных *.
Известны два типа дифракции света на ультразвуке /13/: дифракция Рамана-Ната и дифракция Брэгга. Первая соответствует дифракции света на тонкослойной акустической решетке объемных или поверхностных волн, являющейся аналогом плоской голограммы. Вторая - дифракции на толстослойной решетке - аналоге объемной голограммы. Угловое разделение дифракционных порядков достижимо на акустических решетках с достаточно малой длиной волны. Практически это возможно на ультразвуковых частотах выше 500 КГц - 1 МГц.
Акустооптическая голография имеет два особенности. Первая - получение изображения в реальном масштабе времени - вытекает из характера непосредственного взаимодействия света со звуком.
* С этой точки зрения известный метод поверхностного рельефа жидкости /14,15/ также относится к акустооптическим методам.
- 289 -
Вторая особенность состоит в том, что изображение может восстанавливаться при дифракции света на одной предметной акустической волне без использования дополнительной опорной. Бегущая акустическая волна вызывает лишь доплеровский сдвиг оптической частоты в изображении /16/.
Рассмотрим дифракцию световой волны на объемной акустической решетке, возбужденной в изотропной оптически Прозрачной среде (рис.1).
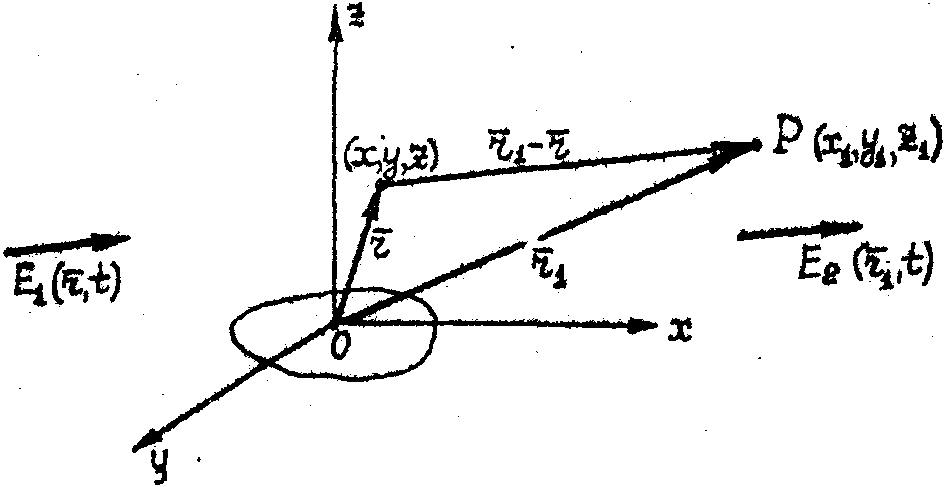
Рис.1. Схема дифракции света на объемной акустической решетке.
1 - акустическое поле 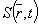 ; ;
2 - источник звука или рассеивающий объект;
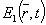 - -
падающее световое поле;
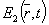 - -
рассеянное световое поле.
Акустические поле 1 бегущей гармонической волны, создаваемое источником звука или рассеивающим объектом 2 в полупространстве Z>0, описывается выражением
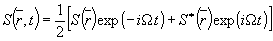 (1) (1)
где 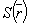 - комплексная амплитуда, W
- круговая частота, - комплексная амплитуда, W
- круговая частота, 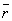 - радиус-вектор точки поля с координатами (x,y,z). - радиус-вектор точки поля с координатами (x,y,z).
- 290 -
Акустическое поле в изотропной среде создает вариацию показателя оптического преломления. В приближении линейной акустики распределение показателя преломления в среде имеет вид:
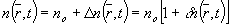 (2) (2)
где no - показатель преломления среды, не возмущенной звуком, 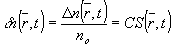 - относительное изменение показателя преломления, С - акустооптическая постоянная среды. - относительное изменение показателя преломления, С - акустооптическая постоянная среды.
В этом приближении интенсивность звука незначительна, и величина d
n лежит в пределах 10-4¸
10-6, что соответствует слабо рассеивающему объекту.
Акустическое поле 1 освещается монохроматической световой волной
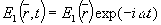 (3) (3)
где 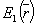 - комплексная амплитуда, w
- частота. - комплексная амплитуда, w
- частота.
Определим рассеянное световое поле 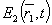 в произвольной точке Р пространства с координатами {x1,y1,z1), где в произвольной точке Р пространства с координатами {x1,y1,z1), где 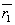 - радиус-вектор точки Р. Общее световое поле в этой точке равно сумме падающего и рассеянного излучений - радиус-вектор точки Р. Общее световое поле в этой точке равно сумме падающего и рассеянного излучений
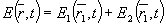 (4) (4)
Так как 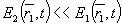 , рассеянное световое поле может быть определено в первом борновском приближении теории возмущений /17/. Задачу можно рассматривать как квазистатическую, учитывая, что скорость света много больше скорости звука. , рассеянное световое поле может быть определено в первом борновском приближении теории возмущений /17/. Задачу можно рассматривать как квазистатическую, учитывая, что скорость света много больше скорости звука.
В общем случае распространение света в акустическом поле описывается волновым уравнением /13/
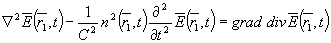 (5) (5)
где С - скорость света в вакууме.
В скалярном случае для изотропной среды 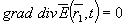
- 291 -
и (5) сводится к однородному уравнению Гельмгольца
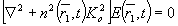 (6) (6)
где 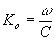 - волновое число. - волновое число.
Подставляем (2) и (4) в (6) и учитываем, что падающая световая волна длине возмущенной звуком среды удовлетворяет однородному уравнению
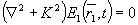 (7) (7)
Тогда при отбрасывании величин второго и более высокого порядка малости получаем неоднородное уравнение Гельмгольца
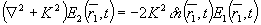 (8) (8)
где K = Ko∙no Решение (8) имеет вид:
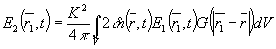 (9) (9)
где 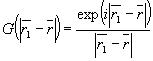 - сферическая функция Грина. - сферическая функция Грина.
Подставляя (1) и (3) в (9), получаем выражения для светового поля в +1 и -1 дифракционных порядках:
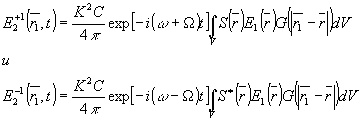 (10) (10)
Нетрудно заметить аналогию акустического поля с объемной оптической голограммой. При дифракции света на объемной голограмме /10/ световое поле в порядках содержит волновую функцию излучения, рассеянного голографируемым объектом, которая и образует его восстановленное изображение. При дифракции света на акустическом
- 292 -
поле в оптических дифракционных порядках (10) содержится его волновая функция 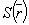 . Поэтому при определенных условиях освещения . Поэтому при определенных условиях освещения 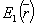 в порядках восстанавливаются изображения акустического поля или расположенных в нем объектов. Изображения в порядках комплексно сопряжены, а оптические частоты смещены относительно частоты освещающей волны на величину доплеровского сдвига ±
W
. в порядках восстанавливаются изображения акустического поля или расположенных в нем объектов. Изображения в порядках комплексно сопряжены, а оптические частоты смещены относительно частоты освещающей волны на величину доплеровского сдвига ±
W
.
Рассмотрим дифракционное акустооптическое взаимодействие в спектральном представлении (рис.2).
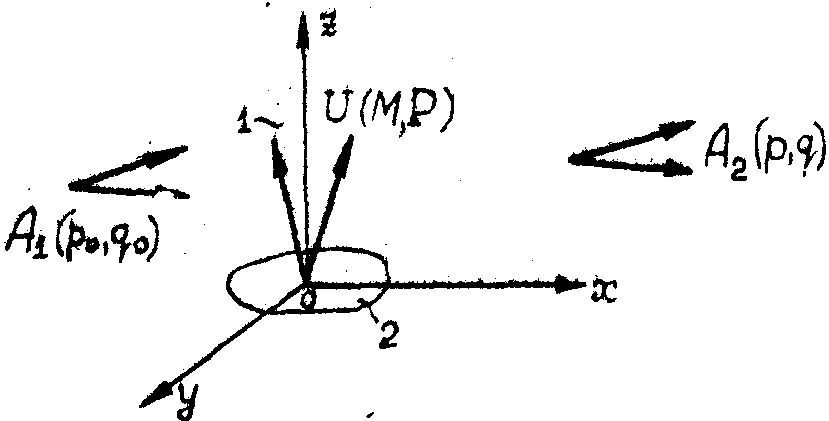
Рис .2. Схема дифракции света на объемной акустической решетке в спектральном представлении.
1 - акустическое поле; 2 - источник звука или рассеивающий объект; A1(po,qo) - угловой спектр падающей световой волны; A2(p,q) - угловой спектр рассеянной световой волны; U(M,P) - угловой спектр акустической волны.
Пространственное распределение светового поля в + 1 порядке
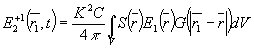 (11) (11)
Акустическое поле 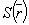 выражается через пространственно-угловой спектр U(M,P) как выражается через пространственно-угловой спектр U(M,P) как
 (12) (12)
- 293 -
где M,P,Q - направляющие косинусы, 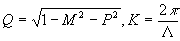 волновое число звука, L
- длина акустической волны. волновое число звука, L
- длина акустической волны.
Падающая световая волна 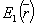 выражается через свой пространственно-угловой спектр A1(po,qo), выражается через свой пространственно-угловой спектр A1(po,qo),
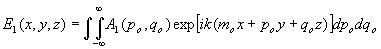 (13) (13)
где mo,po,qo - направляющие косинусы,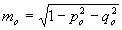 . .
Спектральное представление сферической функции Грина имеет вид:
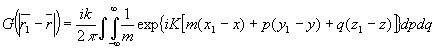 (14) (14)
где m,p,q - направляющие косинусы рассеянной световой волны, 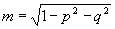 . .
В последующей изложении предполагаются только действительные значения величин Q,, mo и m, что соответствует представлению акустического поля, падающего и рассеянного световых полей через спектральные разложения по плоским волнам, распространяющимся, соответственно, в направлении звука и света.
Подставляя (12) - (14) в (11), получаем
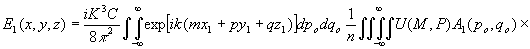
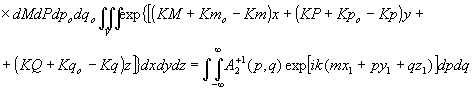 (15) (15)
где А2+1(p,q) - пространственно-угловой спектр рассеянной волны в +1 дифракционной порядке.
При бесконечно большом пространстве акустооптического
- 294 -
взаимодействия объемный интеграл в (15) сводится к трехмерной дельта-функции. Тогда угловой спектр волны в +1 порядке
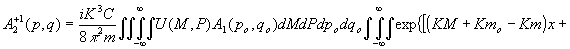
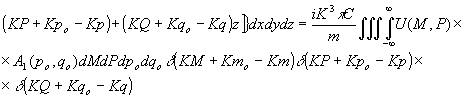 (16) (16)
Аналогично угловой спектр волны в -1 порядке
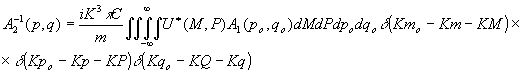 (17) (17)
Появление в (16) и (17) дельта-функций
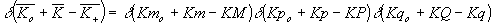
и
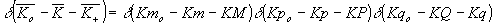
физически означает, что дифракция света на толстослойной акустической решетке эквивалентна брэгговскому рассеянию света, для которого выполняются условия :
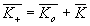
и 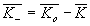 (18) (18)
где 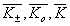 - волновые векторы звуковой волны, падающей и рассеянной в ±1 порядок световых волн, соответственно. Отметим, что условия (18) могут быть получены из закона сохранения импульса для фотон-фононного взаимодействия: - волновые векторы звуковой волны, падающей и рассеянной в ±1 порядок световых волн, соответственно. Отметим, что условия (18) могут быть получены из закона сохранения импульса для фотон-фононного взаимодействия:
- 295 -
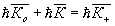
и 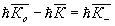
где 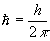 , h - постоянная Планка. Условия (18) и (19) иллюстрируются рис.5. , h - постоянная Планка. Условия (18) и (19) иллюстрируются рис.5.
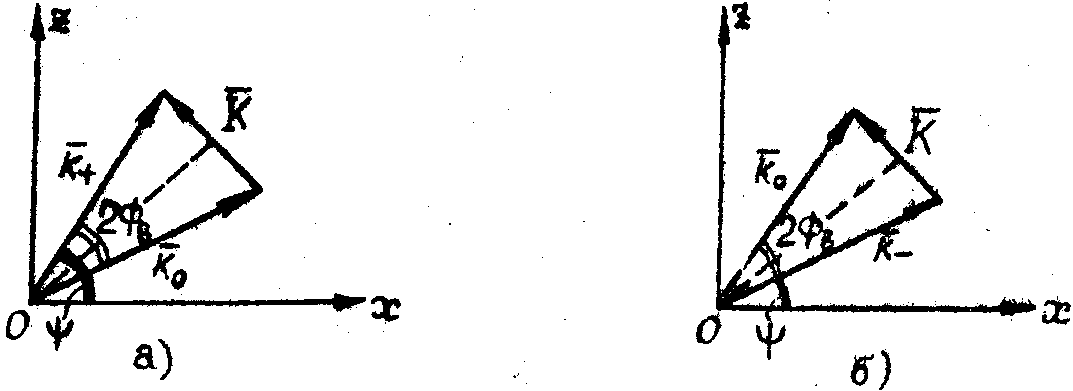
Рис. 3. Векторные диаграммы брэгговской дифракции света на звуке.
а) для +1 порядка; б) для -1 порядка.
Таким образом, каждая спектральная составляющая акустического поля переносится в рассеянное поле, если в спектре освещающей волны содержится плоская волна, направление которой образует брэгговский угол ФВ с фронтом акустической составляющей: 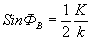 . Полная передача спектра достигается при освещении акустического поля цилиндрической световой волной спектр которой . Полная передача спектра достигается при освещении акустического поля цилиндрической световой волной спектр которой
А 1(p o,q o) = A 1(q o) d
(p o) (19)
Тогда, подставляя (19) в (16), получаем
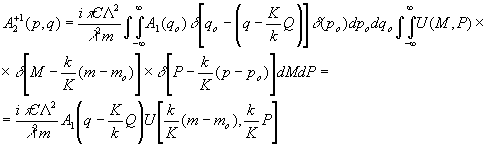 (20) (20)
- 296 -
Аналогично
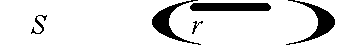 (20) (20)
Как следует из (20)-(21), спектр светового поля в дифракционных порядках представляет собой произведение спектров падающей световой волны и акустического поля. Световое поле в порядках, соответственно, равно свертке освещающего и акустического полей. Следовательно, акустооптическое взаимодействие является изображающим процессом, аналогичным оптическому. Однако пространственные частоты спектров света и звука в произведениях (20) и (21) существенно отличны от исходных, что соответствует определенной трансформации изображений. Правила построения изображения рассматривается в следующем разделе.
2. Изображающие свойства акустических полей
Изображающие свойства дифракции света на объемных и поверхностных акустических волнах и различные методы их использования освещены в значительном количестве работ /5,14-16,19-47/. В первых работах /19,20/ по оптическому зондированию объемных акустических полей методом брэгговской дифракции установлено, что угловая зависимость распределения интенсивности в дифракционном максимуме соответствует угловому спектру мощности акустического поля. Это обстоятельство, подтверждающее свойство переноса спектров в дифракционном взаимодействии, было использовано для получения изображения акустических полей. Впервые изображение методом дифракции на объемных волнах получено А.Корпелом /21/ в 1966 г., и в последующем это явление исследовалось как экспериментально на акустических частотах от 1 до 1000 МГц /23-25,27,34-36,44,46/, так и теоретически /26,38,45,16/. Этому вопросу посвящена монография /5/.
Одновременно с визуализацией полей объемных акустических волн развиваются методы голографии на поверхностных волнах. Первой работой в этом направлении был метод поверхностного рельефа жидкости, предложенный в 1966 г. /21/ и в дальнейшем существенно
- 297 -
усовершенствованный /14,15/. Метод распространен также на акустические поля, возбуждаемые на поверхности твердых тел /32,39/. Интерференционная регистрация полей поверхностных смещений приводит к значительному повышению чувствительности метода. Используются различные способы интерференционной регистрации: гетеродинные /29,33/, модуляционные /40/, многолучевые /41/.
Наряду с методами, в основе которых лежит дифракционный процесс получения изображения, к акустооптической голографии следует отнести известные методы голографической интерферометрии, для которых акустическое поле является фазовым объектом. В этой случае акустическое поле записывается на голограмму при прямом /31,42/ диффузном /30/ или модулированном по частоте /31,43/ лазерном освещении, а голограммы при восстановлении дают изображение поля /30,43/, либо его оптического спектра /31,32,42/
Изображающие свойства поверхностного рельефа, возникающего на границе раздела сред под действием акустической волны подобны известным свойствам тонкой фазовой голограммы /47/. Поверхностный рельеф на границе раздела сред эквивалентен квадратичному оптическому детектору акустического поля, поскольку величина смещений поверхности пропорциональна интенсивности звука. Изображение восстанавливается с поверхностного рельефа, образующегося как в результате интерференции предметной и опорной акустических волн, так и от одной предметной волны /32,43/.В последнем случае имеет место доплеровский частотный сдвиг в изображении.
Рассмотрим процесс образования изображения акустического поля при дифракции на объемных волнах на примере точечного акустического источника (рис.4).
Акустическое поле точечного источника звука S освещаем .;я точечным источником света L. Световая 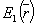 и акустическая и акустическая 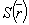 волны в этом случае являются цилиндрическими и описывается соответствующими функциями Ганкеля, которые в спектральном представлении имеют вид: волны в этом случае являются цилиндрическими и описывается соответствующими функциями Ганкеля, которые в спектральном представлении имеют вид:
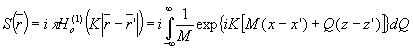 (22) (22)
где 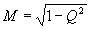 , ,
- 298 -
и
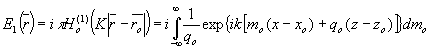 (23) (23)
где 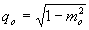 , ,
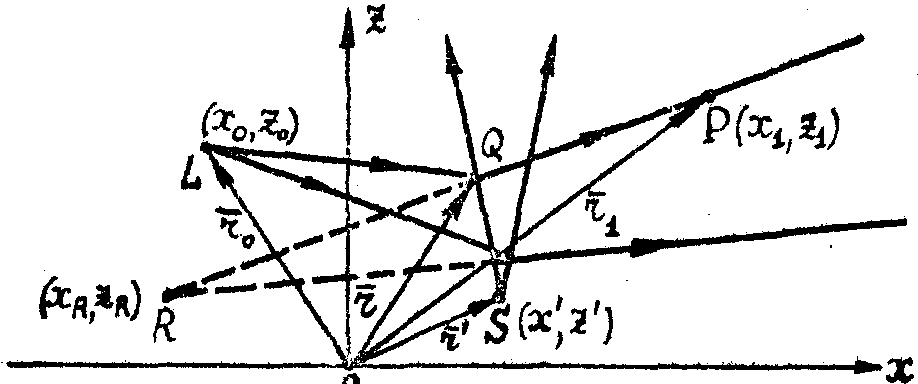
Рис.4. Формирование изображения точечного акустического источника.
L - точечный источник света с координатами (xo,zo); S - точечный акустический источник с координатами (x',z'); R - изображение источника S в +1 дифракционном порядке с координатами (xR,zR); Р - точка рассеянной световой волны +1 порядка; Q - произвольная точка пространства акустооптического взаимодействия; 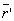 - радиус-вектор источника звука S; - радиус-вектор источника звука S; 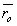 - радиус-вектор источника света L; - радиус-вектор источника света L; 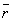 - радиус-вектор произвольной точки Q пространства взаимодействия; - радиус-вектор произвольной точки Q пространства взаимодействия; 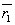 - радиус-вектор точки Р рассеянной световой волны +1 порядка. - радиус-вектор точки Р рассеянной световой волны +1 порядка.
Функция Грина для этого случая в соответствии с (14) имеет вид:
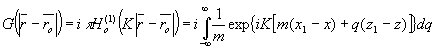 (24) (24)
- 299 -
Подставляя (22)-(24) в (11), получасы выражение для световой волны в +1 порядке:
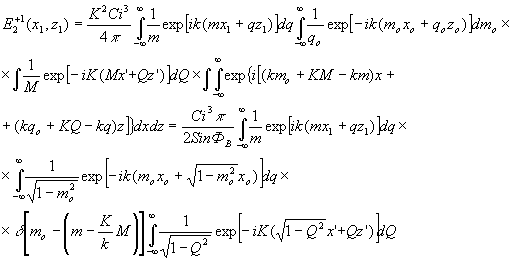 (25) (25)
Интегралы в (25), содержащие d
-функции, определяют пространственные преобразования в изображающем процессе. Определим физический смысл преобразования. Из геометрии брэгговского рассеяния (рис.3а) несложно определить
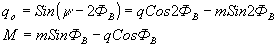 (26) (26)
где m = Cosy
, q = Siny
, y
- угол вектора 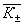 рассеянной световой волны. рассеянной световой волны.
Тогда, подставляя (26) в (25), после преобразований получаем:
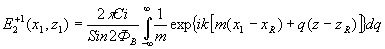 (27) (27)
где
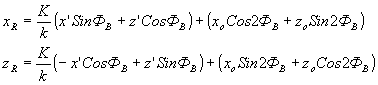 (28) (28)
- 300 -
Нетрудно заметить, что световая волна (27}, рассеянная в +1 порядок также является цилиндрической, а координаты (xR,zR) точки R ее источника определяются (28). Следовательно, точка R является изображением акустического источника S.
Уравнения (28) определяют правила построения изображений источников звука /22,27/
Преобразования (28) состоят в следующем Осуществляется перенос качала координат в точку с координатами (xoCos2ФВ-zosin2ФВ; xoSin2ФВ+zoCos2ФВ), поворот осей на угол 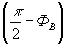 и уменьшения масштаба изображения в и уменьшения масштаба изображения в 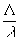 раз. Геометрически это правило легко реализуется построением показанным на рис.5: точки L и S соединяются, и точка R определяется поворотом отрезка LS на угол 2ФВ против часовой стрелки. раз. Геометрически это правило легко реализуется построением показанным на рис.5: точки L и S соединяются, и точка R определяется поворотом отрезка LS на угол 2ФВ против часовой стрелки.
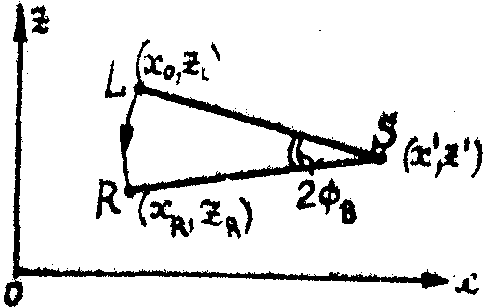
Рис.5 Построение изображения точечного акустического источника:
L - источник света; S - акустический источник; R - изображение.
Повторяя аналогичные выводы для -1 дифракционного порядка и подставляя в (11) выражение для акустического поля
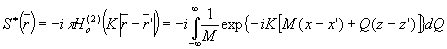
получаем координаты точки R изображения
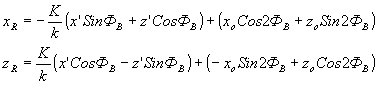 (29) (29)
- 301 -
которые соответствуют переносу начала координат и повороту осей на угол - 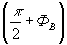 . .
Изображения акустического поля в дифракционных порядках строятся по рассмотренным выше правилам для точечного объекта. На рис.6 представлена схема формирования изображения одномерного объекта - отрезка SS1.
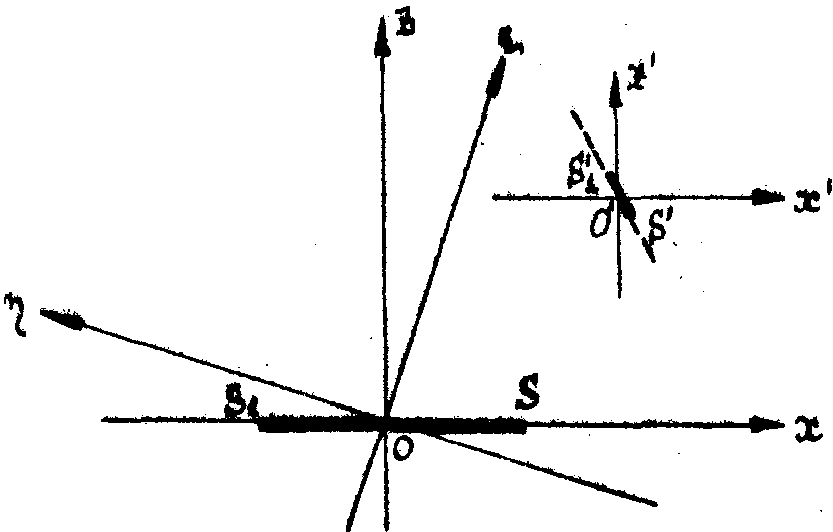
Рис.6. Схема построения изображения акустического объекта:
SS 1 - одномерный объект; S'S'1 - изображение объекта в дифракционных порядках.
Изображение (отрезок S'S'1) передается в дифракционные порядки без искажений с уменьшением в 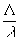 раз. Двумерные объекты передаются с искажениями, так как размеры по оси Y претерпевают масштабные изменения (уменьшение в раз. Двумерные объекты передаются с искажениями, так как размеры по оси Y претерпевают масштабные изменения (уменьшение в 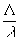 раз), тогда как размеры по оси Х передаются без изменений масштаба. Трехмерные объекты дополнительно искажаются в направлении оси Z. раз), тогда как размеры по оси Х передаются без изменений масштаба. Трехмерные объекты дополнительно искажаются в направлении оси Z.
Визуализация акустических полей и объектов методом дифракции требует достаточно большого оптического увеличения (порядка сотен крат /33,44/, поскольку изображения в порядках сильно уменьшены. Это существенно усложняет реализацию метода для технических приложений. Значительно большее применение дифракционные методы нашли в тех случаях, когда не требуется полной визуализации, например
- 302 -
при оптической исследовании полей. В /19,28/ описаны методы дифракции, используемые для оптического зондирования при исследованиях структуры полей ультразвуковых излучателей.
Литература
1. Acoustical Holography, v.1, N.-Y., 1969; v.2, N.-Y., v.3,1970; N.-Y, 1971
2. Ю.И.Островский. Голография, изд. "Наука", М., 1970.
3. М.Франсон. Голография, изд. "Мир", М., 1972.
4. Методы неразрушающих испытаний, под ред. Р.Шарпа, изд. "Мир", М., 1972.
5. A.Korpel. Optical Imaging of Ultrasonic Fields by Acoustic Bragg Diffraction, Bronder-Offset N.-Y., Rotterdam, 1969.
6. Л.В.Бабин, С.Б.Гуревич. Акустический журнал, 17, 4, 489,1971.
7. Р.Р.Красовский. УФН, 105, 3, 597, 1971.
8. В.И.Телешевский. Материалы I Всесоюзной школы по голографии, Л., стр.442, 1972.
9. Д.Габор. Proc.Roy.Soc., A197, 454. 1949; Proc.Phys.Soc., B64, 449, 1951.
10. Ю.Н.Денисюк. ДАН СССР, 144, 6, 1275, 1962. Оптика и спектроскопия, 14, 4, 522, 1963.
11. Физическая акустика, под ред. У.Мээона, 1A, изд. "Мир", М., 1966.
12. Е.Р.Мустель, В.Н.Парыгин. Методы модуляции и сканирования света, изд. "Наука", М., 1970.
13. С.М.Рытов, Изв. АН СССР, сер.физич., № 2, 223, 1937.
14. B.Brenden. Materials Evaluation, 27, 6, 140, 1969.
15. R. В.Smith, B.B.Brendon. Ultrasonics, 7, 2, 125, 1969.
16. В.И.Какичашвили, Ш.Д.Какичашвили. Акустический журнал, 18, 4, 546, 1972.
17. М.Борн, Э.Вольф. Основы оптики, изд. "Наука", М., 1970.
18. E.Wolf. Optics Communication, 1, 4, 153, 1969.
19. M.G.Kohen, B.J.Gordon. BSTJ, 44, 4, 693, 1965.
20. B.J.Gordon. Proc. I ЕEE, 54, 10, 1429, 1966.
23. R.K.Muller, N.K.Sheridan. Appl.Phys.Lett., 9, 9, 328, 1966.
- 303 -
22. A.Korpel. Appl.Phys.Lett., 9, 12, 425, 1966.
23. C.S.Tsai, H.V.Hance. JASA, 42, 6, 1345, 1967.
24. H.V.Hance, J. К.Parks, C.S.Tsai. J.Appl.Phys., 38, 4, 1981, 1967.
25. J.V.Havlice, C.F.Quate, B.Richardson. IEEE Symp.Sonics Ultrason., p.14, 1967.
26. A.Korpel. IEE Е Trans.Son.Ultrason., SU-15, 3, 153, 1968.
27. A.Korpel. IEEE Spectrum, 5, 10, 45, 1968.
28. W.T.Maloney, G.Meltz, R.L.Gravel. IEEE Trans.Son.Ultrason., SU-15, 3, 167, 1968.
29. G.A.Massey. Proc. IEEE, 56, 12, 2157, 1969.
30. R.P.Salavant, W.G.Alwang, L.A.Cavanaugh, E.Sammarino. JASA, 44, 6, 1732, 1968.
31. A.Alippi, L.Palmieri, Acustica, 20, 2, 84, 1968.
32. A.Korpel, P.Desmares. JASA, 45, 4, 881, 1969.
33. R.L.Whitman, A.Korpel, Appl.Opt., 8, 8, 1567, 1969.
34. J.Landry, J.Powers, G.Wade. Appl.Phys.Lett., 15, 6, 186, 1969.
35. G.Wade, C.J.Landry, A.A.de Souza. Acoustical Holography, 1, Ch.II, 159, 1969.
36. Ueda Mitsuhiro, Sato Takuso. Bull.Tokyo Inst.Techn., 92, 21, 1969.
37. A.Alippi, L.Palmieri. Acustica, 21, 2, 104. 1969.
38. W.H.Carter. JOSA, 60, 10, 1366, 1970.
39. R.L.Whitman. Appl.Opt., 9, 6, 1375, 1970.
40. P.S.Green, A.Macovski, S.D.Hamsey. Appl.Phys.Lett., 16, 7, 265, 1970.
41. R.L.Lauson, B.J.Hunsiger, F.Y.Gho, Appl.Opt., 9, 12, 2805, 1970.
42. И.С.Клименко, В.И.Телешевский, Акустический журнал, 16, 4, 613, 1970.
43. C.C.Aleksoff. Appl.Opt., 10, 6, 1329, 1971.
44. Н.Т.Азаров, В.И.Телешевский. Акустический журнал, 17, 3, 451, 1971.
45. З.И.Фейзулин. Изв.вузов. Радиофизика, 15, 5, 713, 1972.
46. J.Landry, H.Keyani, G.Wade. J.Appl.Phys., 43, 6, 2502, 1972.
- 304 -
47. W.T.Cathey, Appl.Opt., 9, 6, 1478, 1970.
48. Ш.Д.Какичашвили. ЖТФ, 42, 9, 1967, 1972.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

