|
|
 |
 |

|
| |
КАЧЕСТВО ИЗОБРАЖЕНИЯ В ГОЛОГРАФИЧЕСКОМ ТЕЛЕВИДЕНИИ
Д.Ф.Черных
В работе рассмотрены особенности голограммы как объекта передачи, проведен анализ процесса передачи голограммы и определен характер воздействия системы передачи на изображение, восстановленное с переданной голограмм, Показано, что свойства голограммы и характер воздействия системы передачи определяются параметрами схемы голографирования.
Введение
С момента появления первых работ по голографии возникла и получила широкое распространение идея реализации преимуществ голографического метода регистрации изображения в системах передачи изображения на расстояние /1/. Кажется, что очень просто передать изображение интерференционной структуры голограммы, сфотографировать его с экрана и восстановить с полученного негатива изображение объекта, которое может быть трехмерным, цветным и т.п.
Однако уже первые попытки передачи голограмм по каналам связи /2-8/ показали , что существуют значительные препятствия, обусловленные различием в пропускной способности передачи изображения и большой информационной емкостью голограммы. Будем надеяться, что эти трудности будут со временем преодолены.
Необходимо отметить основные отличия обычных систем передачи изобретения от голографических систем передачи изображения.
1. Если обычные системы (телевизионные, фототелеграфные) передают оптическое изображение объекта, то голографические системы имеют дело с интерференционной структурой, в которой содержатся информация об объекте.
2. Если для обычных систем конечным результатом передачи является получение на каком-либо экране изображение объекта то для
- 248 -
голографических систем получение изображения интерференционной структуры является промежуточным этапом, так как конечное изображение восстанавливается с помощью этой структуры .
Из сказанного видно, что особенности голографической системы передачи изображения определяются двухступенчатостью голографического процесса. При передаче голограммы по каналу связи она выступает, с одной стороны, как объект передачи, а с другой стороны, как система формирования изображения. Естественно, что изменения, происшедшие с голограммой в процессе передачи, скажутся на восстановленном изображение. Поэтому третья особенность заключается в характере воздействия систем передачи на передаваемое изображение.
3. Если в обычных системах переучи изображения система воздействует непосредственно на передаваемое изображение, то голографическая система передачи непосредственно монет влиять только на качество передаваемой голограммы, а качество голограммы определяет качество восстановленного изображения.
Эти особенности голографической системы передачи изображения и определяют круг рассматриваемых вопросов: голограмма, как объект передачи, анализ процесса передачи голограммы , выявление особенностей воздействия систем передачи на качество восстановленного изображения.
1. Голограмма как объект передачи
Для описания голограммы как объекта передачи необходимо выбрать, систему параметров, которая соответствовала бы характеристикам систем передачи изображения. Анализ литературы позволил выделить наиболее общие для всех систем параметры:
1) число элементов разложения в кадре;
2) апертурная характеристика системы;
3) характеристика свет-сигнал;
4) спектральная чувствительность системы.
Тогда голограмму необходимо описывать следующими параметрами:
1) число элементов разрешения, подлежащих передаче, определяемое как произведение размера передаваемого участка голограммы на ширину спектра пространственных частот голограммы; 2) контраст структуры голограммы; 3) мощность и длина волны лазерного излучения,
- 249 -
меняемого для получения голограмм непосредственно на мишени передающей телевизионной трубки.
Большая часть этих параметров определяется геометрией голографической схемы, а их связь со структурой голограммы может быть определена из уравнения голограммы.
Рассмотрим общий случай схемы голографирования , показанный на рис.1. В плоскости Р1(u,v) располагается точечный опорный источник (uo,vo); в плоскости Р2 располагается двумерный объект c пропусканием Т(x
,h); в плоскости Р3(x ,у) производится регистрация голограммы. Расстояние от плоскости регистрации до плоскости Р1 обозначим z1, а расстояние между плоскостями Р3 и Р2-z 2
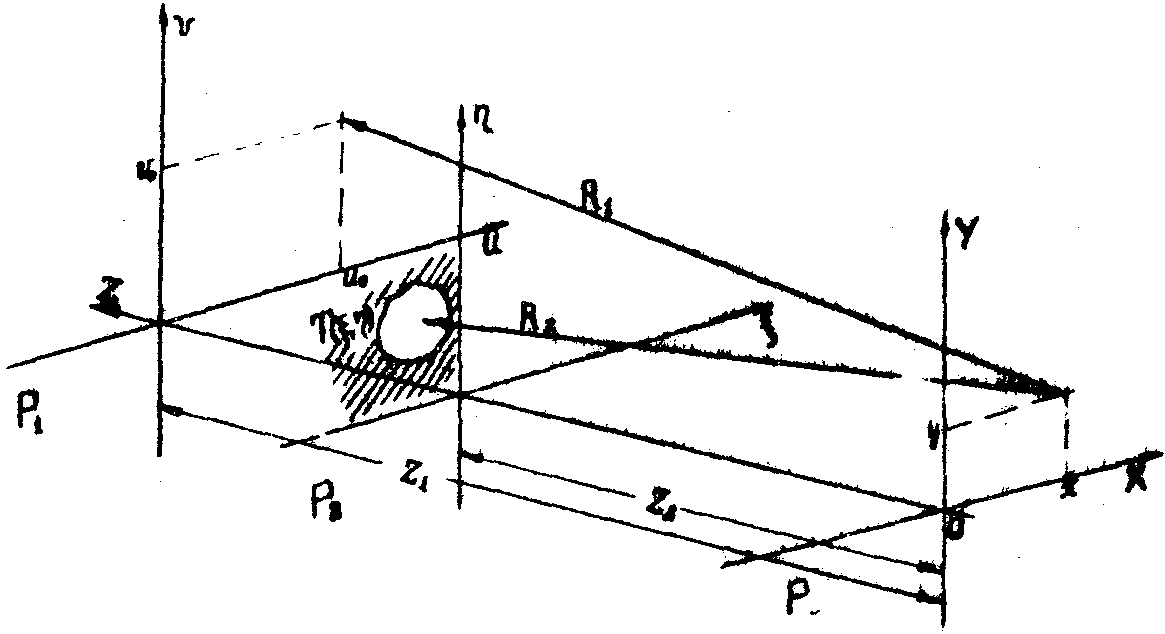
Рис.1. Обобщенная схема получения голограмм.
- 250 -
Тогда распределение амплитуды и фазы волны, излучаемой точечным опорным источником, в плоскости регистрации голограммы будет:
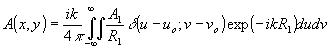 (1) (1)
где А1 - амплитуда опорной волны, d
(u-u0;v-v0) - дельта-функция, описывающая точечный источник, 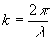 - волновое число. - волновое число.
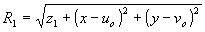
Для объектной волны в плоскости регистрации имеем
 (2) (2)
где А2 амплитуда волны, освещающей объект,
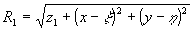
Так как эта интегралы описывают дифракционные картины от опорного источника и объекта, соответственно, то их вид будет различным для различных условий дифракции. В случае дифракции Френеля, которая существует, если 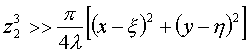 выражения (1) и (2) принимают вид: выражения (1) и (2) принимают вид:
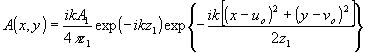 (3) (3)
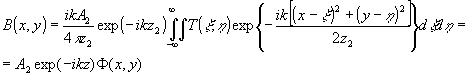 (4) (4)
где F
(х,у) - френелевский образ функции пропускания объекта. В случае дифракции Фраунгофера, реализуемой при 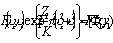 , для (1) и (2) будем иметь , для (1) и (2) будем иметь
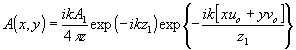 (5) (5)
- 251 -
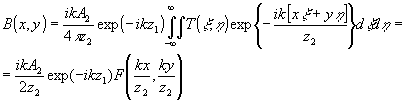 (6) (6)
где 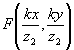 - Фурье-образ функции пропускания объекта. - Фурье-образ функции пропускания объекта.
Изменяя взаимное расположение опорного источника, объекта, и плоскости регистрации, можно получить в плоскости регистрации различные сочетания дифракционных картин от опорного источника и объекта. Нас чаще всего будут интересовать два сочетания.
Первое - точечный опорный источник удален на бесконечность, что идеально выполняет- условия дифракции Фраунгофера, а объект расположен в зоне действия приближения Френеля. Голограмма, образующаяся при этих условиях, называется голограммой Френеля.
Второе сочетание - точечный опорный источник а объект лежат в одной плоскости, находящейся в зоне действия приближения Фраунгофера, которое распространяется также на размер промежутка между опорным источником и центром яркости объекта и размеры регистрирующей поверхности. Голограмма, полученная при таких условиях, называется голограммой Фурье.
Распределение интенсивности в плоскости регистрации для голограммы Френеля и голограммы Фурье будет:
 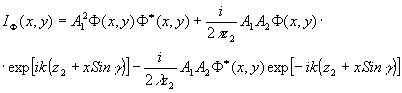 (7) (7)
где g
- угол падения плоской опорной волны;
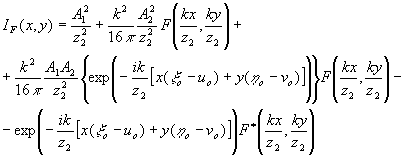 (8) (8)
где x
о, h
о - координаты центра яркости объекта.
- 252 -
Из сравнения этих уравнений следует, что в плоскости регистрации голограммы вид кодирования информации об объекте зависит от расстояния между объектом и плоскостью регистрации, размеров объекта и длину волну применяемого излучения и определяется видом дифракционной картины объекта в плоскости регистрации.
С помощью этих уравнения можно определить параметры, характеризующие голограмму как объект передачи.
Число элементов разрешенья голограммы в каждом из направлений координатных осей определяется произведением ширины спектра пространственных частот, соответствующих этому направлению, на размер голограммы в этом же направлении:
nx = wxdx, ny = wydx (9)
где nx, ny - число элементов разрешения голограммы, wx, wy - ширина спектра пространственных частот голограммы, dx, dy - размер голограммы и направлении Х и y, соответственно. Полное число элементов разрешения голограммы будет определяться
n2 = nxny = wxwydxdy = wxwys (10)
где s - площадь голограммы.
Ширина спектра пространственных частот голограммы является функцией геометрических параметров схемы голографирования. Для выяснения этой зависимости рассмотрим спектр пространственных частот голограммы точечного объекта (x
,h
,z2). Опорная волна излучается другим точечным источником (u,v,z1). Расположение источников показано на рис.2. Для простоты будем рассматривать одномерный случай, полагая, что оба источника излучают волны с единичной амплитудой.
С учетом френелевского приближения распределения амплитуд в плоскости регистрации голограммы, создаваемые точечным источником-объектом и опорным точечным источником будут, соответственно, описываться:
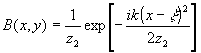 (11) (11)
- 253 -
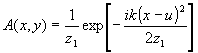 (12) (12)
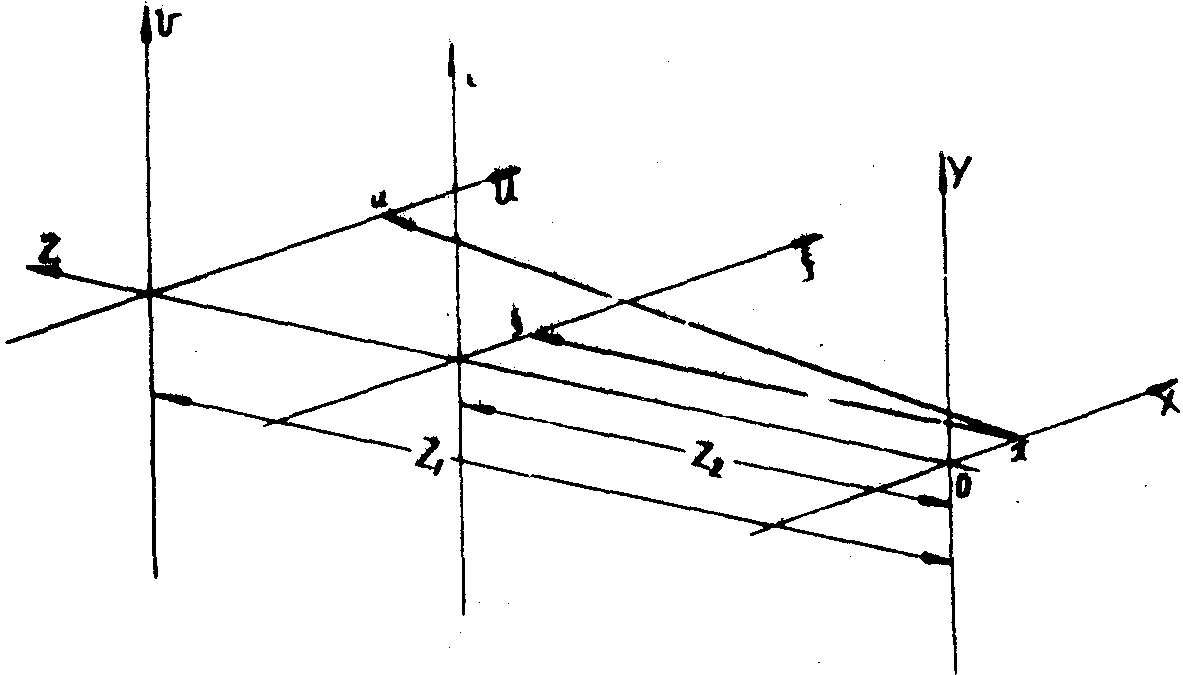
Рис.2. Схема получения голограммы точечного объекта.
Результирующее распределение интенсивности в плоскости регистрации голограмм, обусловленное интерференцией между этими волнами, определяется:
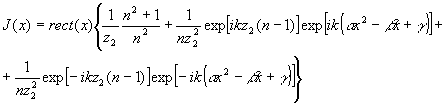 (13) (13)
- 254 -
где rect(x) - функция, учитывающая размеры и прямоугольную форму регистрирующего устройства,
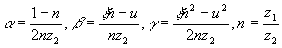
Для определения спектра пространственных частот этого распределения интенсивности найдем его Фурье-образ:
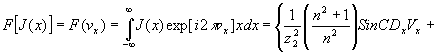 (14) (14)
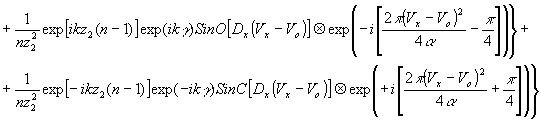
где f - оператор Фурье-преобразования,
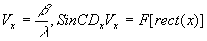
а знак Ä
обозначает операцию свертки.
Выражение для спектра пространственных частот распределения интенсивности интерференционной картина в плоскости регистрации напоминает уравнение изображения, восстановленного с голограммы, и имеет три составляющих. Первая из этих составляющих, соответствующая постоянной составляющей распределения интенсивности , обусловленной засветкой объектной и опорной волнами, располагается в начале координат пространственных частот. Ширина области пространственных частот, определяемая этой составляющей спектра, в данном случае будет зависеть только от размеров голограммы.
Области спектра пространственных частот, описываемые второй и третьей составляющими, характеризуют полосу пространственных частот, соответствующих точечному объекту, и расположены симметрично по обе стороны относительно нулевой частоты, причем центры этих областей смещены от нулевой частоты в направлении на величины ±
vох, соответственно. Вид этих областей определяется сверткой импульсной реакции апертуры регистрирующего устройства с функцией Френеля.
- 255--
Если продолжить аналогии между спектром пространственных частот и изображением, восстановленным с голограммы при помощи сходящейся волны exp(i2p
vx,x), то можно отметить ряд общих моментов. Рассмотрим схему восстановления изображение с голограммы, представленную на рис.3.
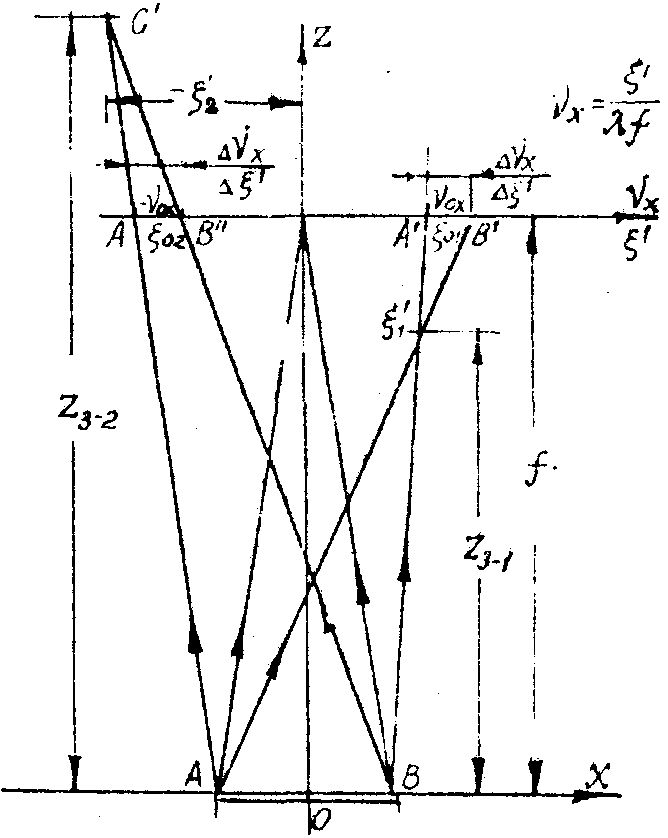
Рис.3. К расчету ширины спектра пространственных частот голограммы точечного объекта.
Известно, что распределение амплитуд в фокальной плоскости сходящейся сферической волны с точностью до квадратичного фазового множителя представляет собой Фурье-образ предмета, через который проходит эта волна.
Эта же волна при прохождении через голограмму будет восстанавливать два действительных сопряженных относительно точки фокуса изображения. Координаты (z3-1,x
’1;z3-1,x
’2) восстановленных изображений точечных источников можно определять через координаты точечного объекта (x
,z2), опорного источника (u,z1) и точечного источника восстанавливающей волны (x
10,¦
) при помощи
- 256 -
масштабных соотношений /9/, которые в нашем случае примут вид:
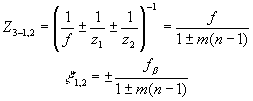 (15) (15)
где 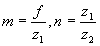
Из схемы восстановления изображения (рис.3) видно, что вид второй и третьей составляющих спектра голограммы точечного объекта можно представить как расфокусированное изображение точечного объекта в фокальной плоскости сходящейся волны. С помощью рис.3 легко определить ширину D
x
’ каждого расфокусированного изображения с точностью до ширины функции sinСdxvx. Из подобия треугольников D
АВС и D
a’b’c’; D
aВС’ и D
А"В"С" следует, что
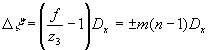 (16) (16)
а координаты центра расфокусированного изображения
x
'0102 = ±
¦
b
(17)
Переходя от пространственных координат к пространственно-частотным координатам, получаем, что в спектре голограммы точечному объекту соответствуют две полосы частот ,
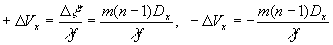 (18) (18)
с центрам 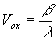 и и 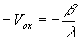 , соответственно. , соответственно.
Тогда полная ширина спектра пространственных частот голограммы точечного объекта будет:
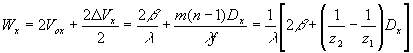 (19) (19)
- 257-
Из выражения (19) следует, что ширина спектра пространственных частот голограммы точечного объекта полностью определяется параметрами схемы голографирования и размером голограммы.
Анализ этого уравнения показывает, что ширина спектра пространственных частот голограммы точечного объекта становится минимальной, тогда точечный объект и опорный источник лежат в одной плоскости (z1 = z2), т.е. в случае голограммы Фурье. При этом ширина спектра, описываемая (19), становится
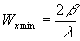 (20) (20)
Для схемы получения френелевской голограммы при z1®
¥
ширина спектра пространственных частот голограммы будет
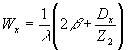 (21) (21)
Таким образом, минимальная ширина спектра пространственных частот при одинаковых значениях пространственной несущей частоты достигается в схеме голографии Фурье, а во всех остальных случаях ширина спектра пространственных частот голограммы будет больше.
Для практики наибольший интерес представляют ширина спектра пространственных частот голограммы сложного объекта. Пользуясь аналогичными рассуждениями, определим ширину спектра пространственных частот голограммы двумерного объекта с максимальными поперечными размерами D
x
=lx
и D
h
=lh
, функцией пропускания t(x
1+x
0h
), с центром яркости, расположенным в точке (x
о,0,z2) Сферическая опорная волна испускается точечным опорным источником с координатами (u,0,z1). С учетом френелевского приближения получаем распределение интенсивности в плоскости регистрации:
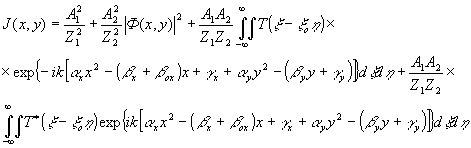 (22) (22)
- 258 -
где
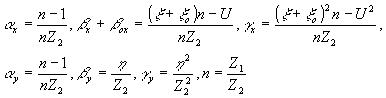
Определим спектр пространственных частот голограммы , подразумевая, что процесс регистрации полученного распределения интенсивности был линейным, и опуская для упрощения постоянные множители и коэффициенты:
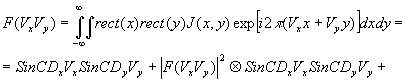 (23) (23)
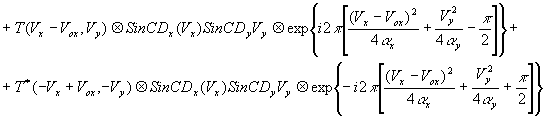
где t(vx,vy) - функции пропускания объекта в плоскости пространственно-частотных координат.
Выражение дня спектра пространственных частот голограммы состоит из четырех слагаемых, первое из которых соответствует спектру постоянной составляющей, обусловленной засветкой опорной волной, и расположено в начале координат пространственных частот, второе слагаемое соответствует спектру засветки объектной волной, представляет из себя автокорреляционную функцию объекта и расположено в околонулевой области пространственных частот.
Шарина полосы частот, занимаемая первым слагаемым, определяется шириной импульсного отклика апертуры голограммы, а ширина полосы пространственных частот, занимаемой вторым слагаемым, равна удвоенной ширине полосы частот, соответствующей объекту в спектре пространственных частот голограммы.
Два последних слагаемых расположёны симметрично относительно нулевой пространственной частоты и смещены относительно её на величину пространственной несущей.
- 259 -
Вновь рассматривая спектры голограммы и изображения, восстановленного с неё при помощи волны exp(i2p
(vxx+vyy), можно сказать, что в фокальной плоскости этой волны находятся два сопряженных расфокусированных изображения объекта, причем, расфокусировка описывается сверткой функции пропускания объекта с френелевской функцией
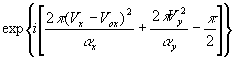
а функция sincdxvx∙sincdyvy является аппаратной функцией голограммы.
Координаты крайних точек таких изображений находятся из соотношений:
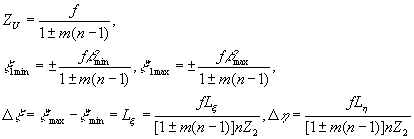 (24) (24)
Координаты центра яркости восстановленного изображения.
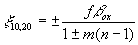 (25) (25)
С помощью рис.4 и этих данных определяем ширину полосы частот, соответствующей объекту, в спектре пространственных частот голограммы:
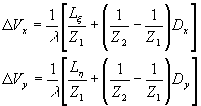 (26) (26)
- 260 -
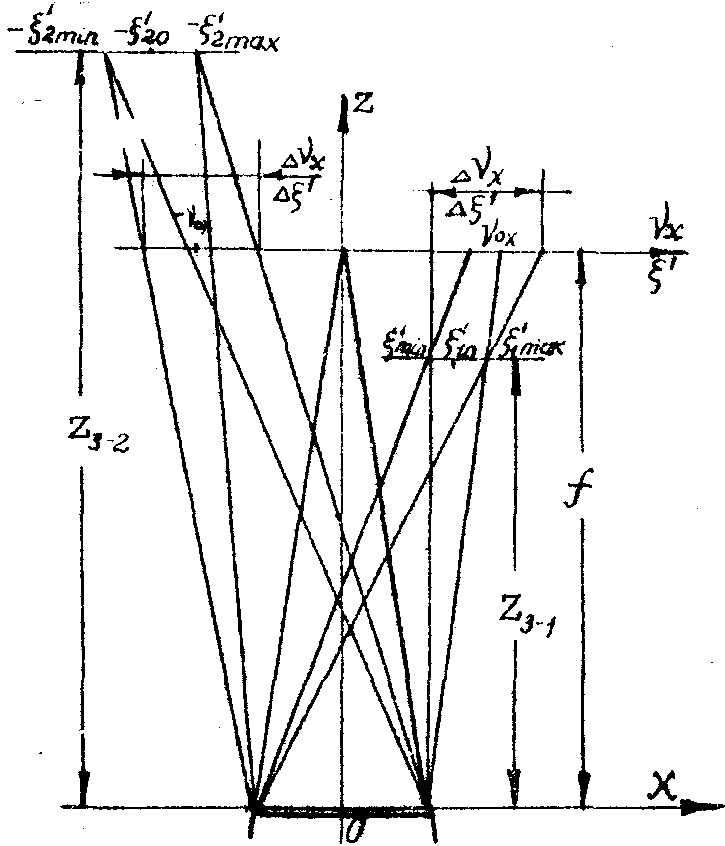
Рис.4. К расчету ширины спектра пространственных частот голограммы двумерного объекта.
а полная ширина спектра пространственных частот голограммы будет:
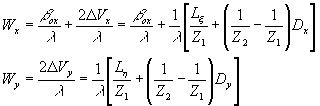 (27) (27)
Величина несущей пространственной частоты 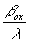 должна быть выбрана такой, чтобы не произошло перекрытия полосы пространственных частот, соответствующей объекту, с полосой частот, соответствующей автокорреляционной функции объекта, т.е. должна быть выбрана такой, чтобы не произошло перекрытия полосы пространственных частот, соответствующей объекту, с полосой частот, соответствующей автокорреляционной функции объекта, т.е. 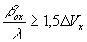 , тогда , тогда
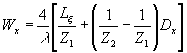 (28) (28)
- 261 -
Для частных случаев голограммы Френеля и голограммы Фурье выражения (27) и (28) примут вид:
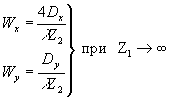 (29) (29)
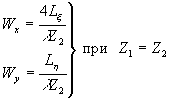 (30) (30)
а в общем случае
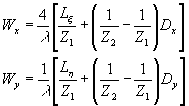 (31) (31)
Из этих выражений видны существенные отличия в свойствах голограмм Френеля и голограмм Фурье. Если ширина спектра пространственных частот голограммы Френеля зависит только от размеров голограммы, то ширина спектра пространственных частот голограммы Фурье зависит от размеров объекта. Эти отличия в свойствах голограмм обусловлены, прежде всего, видом кодирования информации об объекте в спектре пространственных частот голограммы.
На первый взгляд кажется, что вид кодирования информации об объекте, содержащейся в спектре голограммы, зависит только от вида кодирования информации в самой голограмме, который, как было отмечено выше, определяется видом дифракционной картины объекта в плоскости регистрации. В действительности, значительную роль в формировании вида кодирования информации об объекте в процессе голографирования будет играть тип применяемой опорной волны или, другими словами, месторасположения точечного опорного источника. Рассматривая рис.4 можно заметить, что спектр пространственных частот голограммы содержит в себе дифракционные картины сопряженных изображений объекта, восстановленных сходящейся сферической волной. Подставляя себе этот рисунок как схему голографирования, можно
- 262 -
сказать, что вид кодирования информации об объекте в спектре пространственных частот голограммы определяется видом дифракционной картины, создаваемой объектом в плоскости точечного опорного источника.
При этих условиях для френелевской голограммы, т.е. при z1®
¥
, дифракционная картина от объекта в плоскости точечного опорного источника всегда будет соответствовать условиям дифракции в дальней зоне и представлять собой спектр пространственных частот объекта независимо от вида дифракционной картины в плоскости регистрации.
Если z1>z2 и z2>z1>0, то вид дифракционной картины создаваемой объектом в плоскости опорного источника будет определяться разностью расстояний z1 и z2 будет представлять собой френелевскую дифракционную картину.
В случае голограммы Фурье объект располагается в плоскости точечного опорного источника. При этом информация не кодируется, а ширина спектра пространственных частот определяется размерами голографируемого объекта. Из этого следует также, что в плоскости регистрации всегда будет фиксироваться спектр пространственных частот объекта.
Приведенные рассуждения можно подтвердить и аналитически. Рассмотрим спектр пространственных частот одного из последних двух слагаемых уравнения /7/ голограммы Френеля:
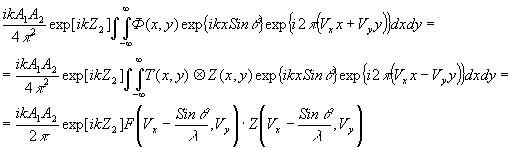 (32) (32)
где (х,у) - функция Френеля, f(vx,vy) - Фурье-образ функции пропускания объекта, z(vx,vy) - Фурье-образ френелевской функция.
Аналогичную операцию проделаем с одним из двух слагаемых уравнения (6), описывающего структуру голограммы Фурье:
- 263 -
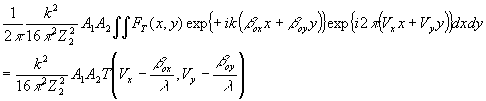 (33) (33)
где
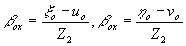
Учитывая, что в спектр пространственных частот голограммы Френеля входит спектр пространственных частот объекта, можно переписать выражение для ширины спектра Пространственных частот в виде:
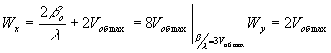 (34) (34)
где vобmax - наибольшая пространственная частота в спектре объекта. Сравнивая выражения (30) и (34), можно сказать, что размер голограммы определяется максимальной пространственной частотой объекта- и обратно:
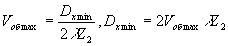 (35) (35)
Окончательно число элементов разрешения будет
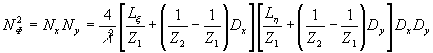 (36) (36)
для голограммы Френеля
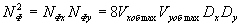 (36) (36)
для голограммы Фурье
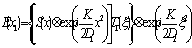 (36) (36)
- 264 -
Особенности структуры голограммы проявляются в анизотропии спектра пространственных частот голограммы , ибо во всех рассмотренных случаях ширина спектра в направлении vx всегда больше, чем в направлении vy (при прочих равных условиях). Типичный спектр пространственных частот голограммы изображен на рис.5.
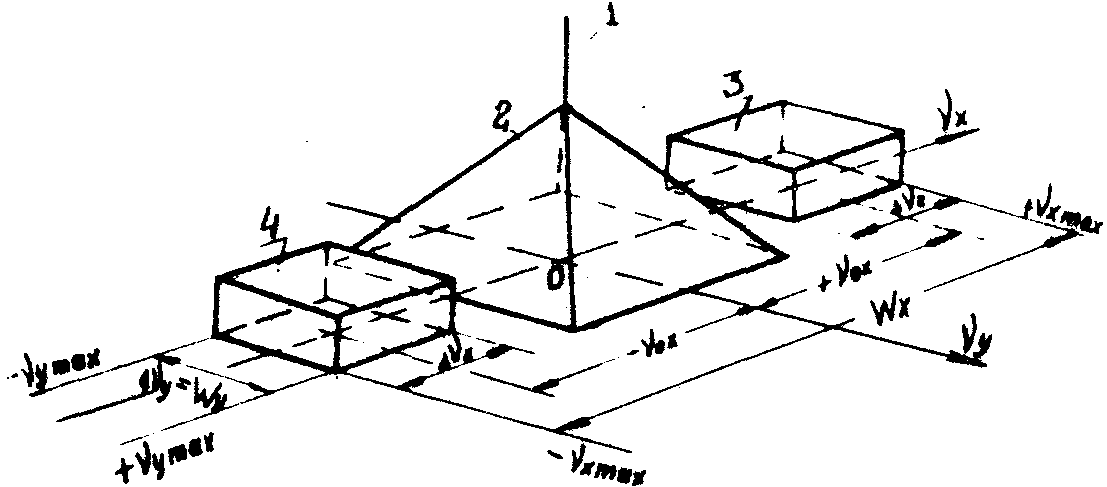
Рис.5. Типичный спектр пространственных частот голограммы.
1 - функция автокорреляции пространственного распределения амплитуды опорной волны в плоскости регистрации, 2 - функция автокорреляции функции пропускания объекта, 3 - полоса частот в спектре голограммы, соответствующая объекту, 4 - сопряженная полоса частот, соответствующая объекту, vо - несущая пространственная частота, vxmax та - максимальная пространственная частота спектра голограммы в направлении x, D
vx - ширина полосы частот, соответствующей объекту, w - ширина спектра пространственных частот голограммы.
Эту особенность структуры голограммы необходимо учитывать при ориентации растра передающего устройства относительно структуры голограммы, подлежащей передаче.
Контраст интерференционной структуры голограммы определяется соотношением амплитуд опорной и объектной волн в плоскости регистрации. Обычно контраст изображения определяют по формуле:
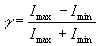 (39) (39)
- 265-
Из уравнения голограммы следует, что.
imax = |
a(x,y)|
2+|
a(x,y)|
2+2a(x,y)∙b(x,y)
imin = |
a(x,y)|
2+|
b(x,y)|
2-2a(x,y)∙b(x,y) (40)
где a(x,y) - амплитуда опорной волны в плоскости регистрации, b(x,y) - амплитуда объектной волны в плоскости регистрации.
Тогда
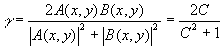 (41) (41)
где 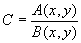
На практике амплитуда опорной волны выбирается примерно на порядок выше амплитуды объектной волны, т.е. С »
10, тогда контраст интерференционной структуры будет g
»
0,1.
Выбор такого соотношения позволяет значительно ослабить низкочастотную составляющую спектра пространственных частот голограммы и тем самым, уменьшить значение пространственной несущей частоты для того, чтобы сузить полосу пространственных частот голограммы.
Передающие телевизионные трубки, наоборот, требуют в силу несовершенной частотно-контрастной характеристики повышенного контраста интерференционной структуры. Поэтому, при передаче голограммы необходимо искать оптимальное решение при выборе контраста структуры и полосы пространственных частот голограммы для согласования с частотно-контрастной характеристикой передающей трубки , чтобы получить высокое качество восстановленного изображения.
2. Анализ процесса передачи голограммы
Блок-схема голографической системы передачи изображения в самом общем виде приведена на рис.6. За исключением блока формирования голограммы здесь есть три основных блока, принадлежащих всем системам передачи изображений: передающее устройство, канал
- 266 -
связи и устройство воспроизведения переданного изображения. Рассмотрим влияние каждого из этих блоков на качество переданной голограммы (точнее, на качество изображения переданной голограммы).

Рис. 6. Блок-схема голографической телевизионной системы.
1 - объект. 2 – схема голографирования, 3 - передающее устройство,  канал связи, 4 - устройство формирования голограммы, 5 - схема восстановления изображения, 6 - восстановленное изображение (действительное). канал связи, 4 - устройство формирования голограммы, 5 - схема восстановления изображения, 6 - восстановленное изображение (действительное).
Передающее устройство, независимо от принципа его действия, позволяет из двумерного распределения интенсивности j(x,у) на входе получить одномерный электрический сигнал ¦
1(t) на выходе. Основой этого процесса служит сканирование пространственного распределения интенсивности света анализирующей апертурой s(e
, ) достаточно малых размеров, чтобы получить последовательное во времени изменение освещенности от элемента к элементу, и в дальнейшем преобразование этой переменной во времени освещенности в адекватный электрический сигнал. ) достаточно малых размеров, чтобы получить последовательное во времени изменение освещенности от элемента к элементу, и в дальнейшем преобразование этой переменной во времени освещенности в адекватный электрический сигнал.
Важнейшими параметрами передающего устройства будут: число элементов разложения, зависящее от площади анализирующей апертуры а размеров растра по строке и кадру, характеристика свет-сигнал, неравномерность чувствительности фотослоя по площади, шумы передающего устройства.
Рассмотрим анализируемое распределение интенсивности j(x,y),
- 267-
ограниченное размерами растра dx и dy в направлениях Х и У, соответственно. Анализирующая апертура сканирует это распределение в направлении Х со скоростью vx, образуя в направлении У последовательный ряд из n строк, отстоящих друг от друга на D
у=b, как показано на рис.7.
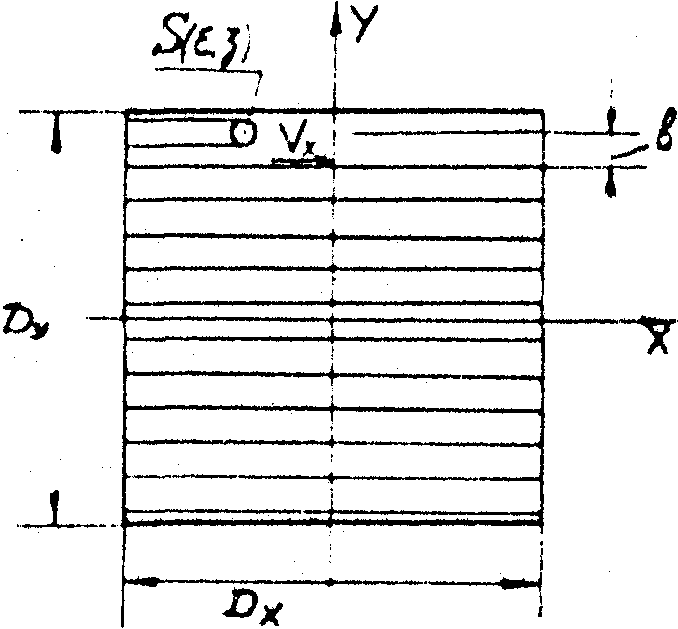
Рис. 7. Формирование телевизионного растра.
dx , dу размеры голограммы, b - расстояние между строками, s(e
, ) - сканирующая апертура, vx - скорость сканирования. ) - сканирующая апертура, vx - скорость сканирования.
Из рисунка видно, что процесс формирования растра является анизотропным; вдоль оси Х анализирующая апертура движется непрерывно, а вдоль оси У переход от строки к строка происходит дискретно.
Естественно, что и математическое описание процесса формирования строки и кадра будет различным : в первом случае, основной операцией будет свертка функции, описывавшей анализирующую апертуру с распределением интенсивности, а во второй - выборка уровней, по которым будет двигаться апертура.
Если использовать идеальную, точечную сканирующую апертуру, которую можно описать дельта-функцией, то распределение интенсивности вдоль траектории сканирования с учетом основных свойств
- 268 –
дельта-функции /10/ можно представить в виде
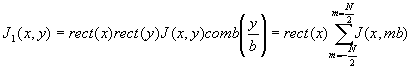 (42) (42)
где 
Так как сканирование - процесс, идущий во времени, то координаты точек растра удобно выразить через время:
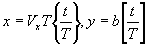 (43) (43)
где 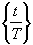 - дробная часть числа, - дробная часть числа, 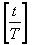 - целая часть числа, t - время, Т - время сканирования одной строки. - целая часть числа, t - время, Т - время сканирования одной строки.
Временной электрический сигнал на выходе передающего устройства с учетом влияния реальной анализирующей апертуры конечных размеров, описываемой функцией s(e
, ), представляет из себя ряд неперекрывающихся временных функций, каждая из которых описывает сигнал соответствующей отроки растра: ), представляет из себя ряд неперекрывающихся временных функций, каждая из которых описывает сигнал соответствующей отроки растра:
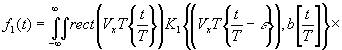
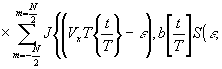 
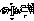  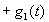 (44) (44)
где 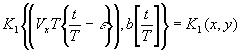 коэффициент, учитывающий коэффициент, учитывающий
- 269 -
неравномерность преобразования интенсивности света в электрический сигнал. В общем случае характеристика свет-сигнал является нелинейной, но поскольку даже в этом случае стремятся работать на линейном участке этой характеристики, то и мы будем считать этот процесс линейным; g1(t) - шум на выходе передающего устройства, источниками которых могут быть: дробовой эффект эмиссионных процессов в передающих телевизионных трубках, тепловые флуктуационные токи в проводниках, шумы предварительного усилителя. Предполагается, что размер сканирующей апертуры мал по сравнению с длиной строки, так что искажениями на краях строки можно пренебречь.
Полученный временной сигнал проходит через канал связи, который можно характеризовать как линейный фильтр с импульсным откликом h(t'} и шумом канала - g2(t). Сигнал на выходе канала связи будет определяться
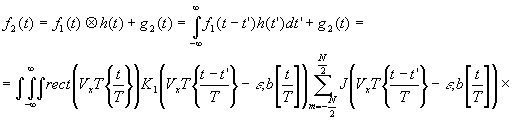 (45) (45)
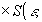 
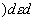  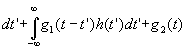
при условии, что ширина импульсного отклика канала связи t'<<t, и, следовательно, искажениями фронтов строчных импульсов можно пренебречь.
С выхода канала связи этот сигнал поступает на вход устройства воспроизведения изображения, которое в голографических системах передачи изображения должно преобразовывать временной электрический сигнал в двумерное распределение одного из оптических параметров среды – коэффициента пропускания (отражения), толщины или коэффициента преломления - с тем, чтобы получать восстановленное с переданной голограммы изображение в реальном времени.
Пусть под действием сфокусированного электронного пучка, модулированного видеосигналом, изменится коэффициент пропускания среды (фотохромного материала). Сфокусированный электронный пучок, распределение энергии в фокусе которого описывается функцией
- 270 -
r(e
, ) ) сканирует синхронно с анализирующей апертурой поверхность фотохромного материала, формируя пространственное распределение коэффициента пропускания. Если скорость сканирования в направлении x1-vx, а промежуток между строками D
y1=b1, то временную координату каждой точки растра устройства воспроизведения можно представить как:
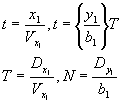 (46) (46)
где dx и dy - размеры сформированного растра в направлениях x1 и y1, соответственно.
Тогда распределение коэффициента пропускания будет:
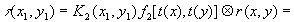
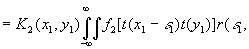 
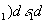  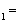
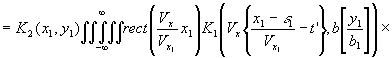
(47)
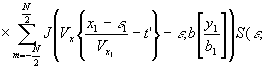 
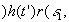  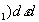  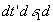  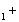
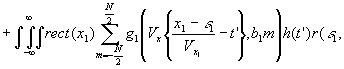 
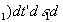  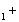
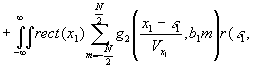 
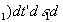  
- 271 -
где t
(х1,у1) - распределение коэффициента пропускания, К2(х1,у1) - коэффициент, учитывающий процесс преобразования сигнал-пропускание, который мы будем считать линейный.
В полученном выражении первое слагаемое описывает изображение переданного распределения интенсивности, положенного на фотохромном материале, а два других слагаемых описывают шумы, сопровождающие это изображение и обусловленные передающим устройством (второе слагаемое) и каналом связи (третье слагаемое).
Действие апертурной характеристики передающего устройства, импульсного отклика канала связи и апертурной характеристики устройства воспроизведения можно заменить эквивалентным влиянием апертурной характеристики cистeмы передачи изображения. Кроме этого, приведем, как это принято, шумы ко входу передающей системы, что в нашем случае означает перевод шумов в плоскость передаваемого распределения интенсивности. С учетом этого выражение (47) примет вид:
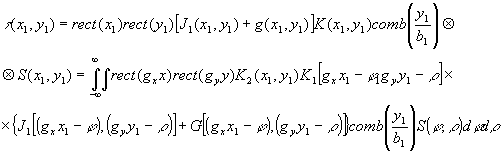 (48) (48)
где 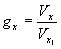 и и 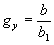 масштабные коэффициенты. масштабные коэффициенты.
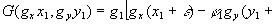 
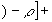
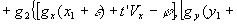 
 (49) (49)
- шумы, приведенные ко входу, а
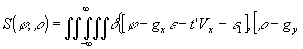 
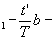  
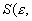 
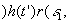  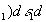  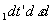  (50) (50)
- 272 -
s(j
,r
) - апертурная характеристика системы передачи изображения.
Современные голографические системы передачи изображения использует в качестве основы телевизионную или фототелеграфную системы, что требует пересъемки изображения переданной голограммы либо с экрана кинескопа, либо с фототелеграфного бланка. В этом случае необходимо учитывать, помимо апертурной характеристики системы передачи, апертурную характеристику оптики, разрешающую способность фотопленки и ее шумы. Однако это не приведет к принципиальным изменениям выражения (48), а только еще более усложнит его.
Получив выражение (48), описывающее влияние системы передачи на голограмму, перейдем к анализу воздействия системы передачи на восстановленное с этой голограммы изображение.
3. Влияние системы передачи на восстановленное изображение
Рассмотрим процесс восстановления изображения с переданной голограммы с учетом влияния некоторых параметров системы передачи, а именно: импульсного отклика всей системы передачи изображения s(j
,r
) размеров переданной голограммы, которые определяются размерами растра dx1 и dy1 промежутка между строками b1. В свете вышесказанного уравнение (48) перепишем в виде
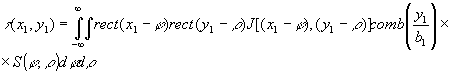 (51) (51)
Так как распределение интенсивности в плоскости регистрации j(x1,y1) различно для каждой схемы голографирования, то будем рассматривать процесс восстановления изображения с каждого типа голограмм отдельно.
а) Восстановление изображения о голограммы Фурье
Уравнение переданной голограммы Фурье получаем путем подстановки (8) в (51):
- 273 -
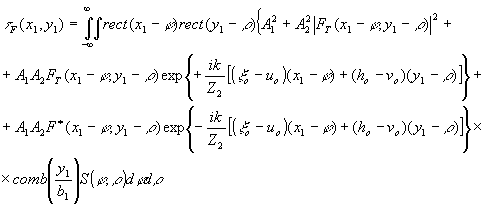 (52) (52)
Если голограмма находится в плоскости регистрации (см. рис. 8) и освещена светом, излучаемым точечным источником, расположенным в точке (ub,vb,z3), то с учетом распределения амплитуды и фазы восстанавливающей волны в плоскости голограммы, определяемым выражением (5), уравнение распределения амплитуды и фазы волны за голограммой будет
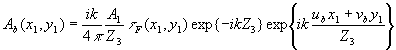 (53) (53)
Так как t
f(x 1,y 1) представляет из себя сумму четырех слагаемых, то можно сказать, что за голограммой присутствуют четыре волны света, появившиеся в результате дифракции восстанавливающей волны на структуре голограммы. Первая из волн сохраняет направление распространения восстанавливающей волны, а направление распространения остальных волн определяется изменением фазы восстанавливающей волны комплексными составляющими каждого из остальных трех слагаемых.
Рассмотрим изображения, формируемые этими волнами в некоторой плоскости Р4, параллельной плоскости голограммы и удаленной от нее на расстояние z4. Распределение амплитуд и фаз в плоскости изображения можно определить с помощью интеграла Кирхгофа:
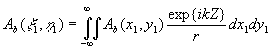 (54) (54)
- 274 -
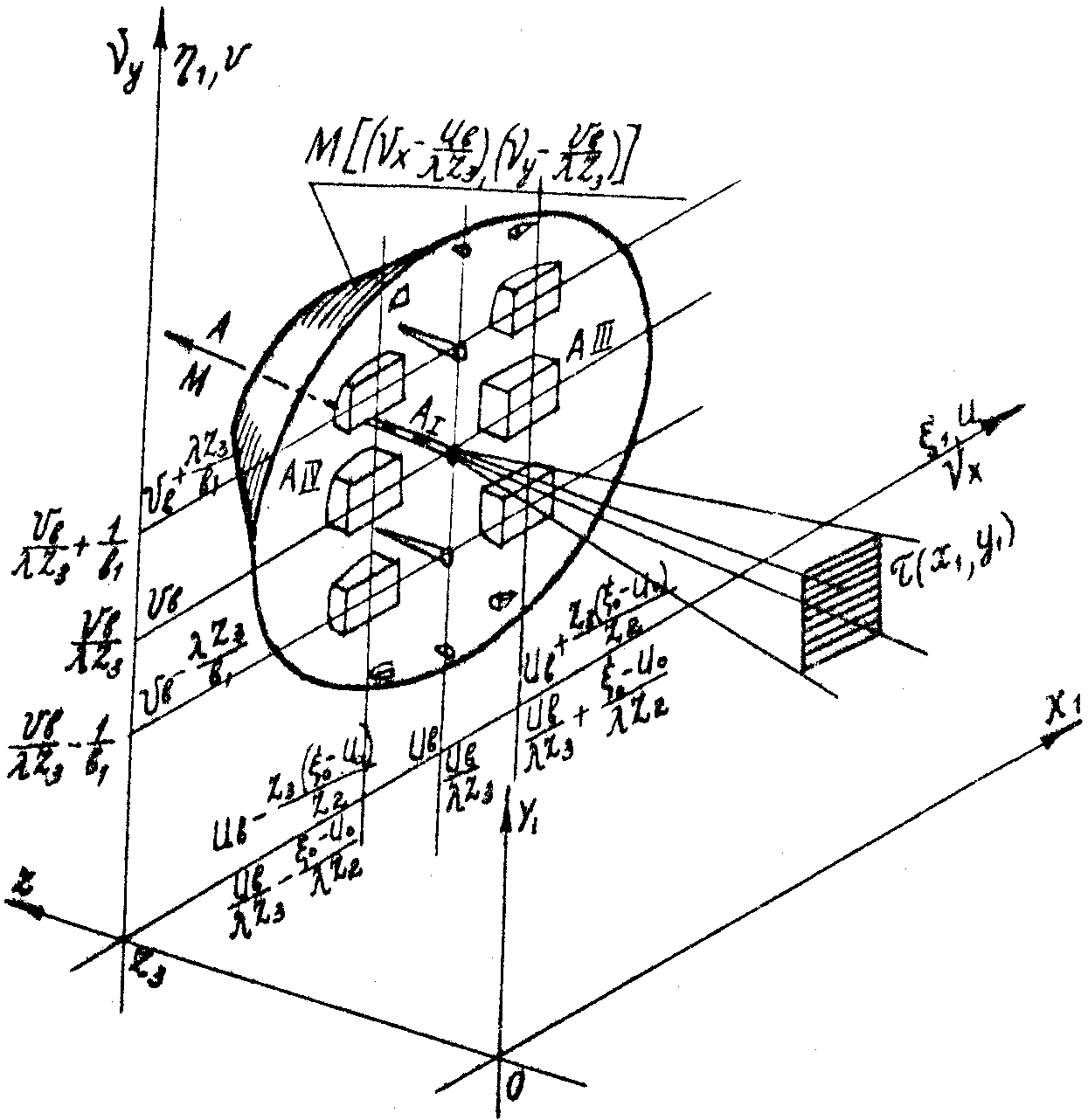
Рио.8. Изображение, восстановленное с переданной голограммы Фурье (при h
-vo=0).
- 275 -
Представляя r через координаты голограммы (х1,у1) и координаты восстановленного изображения (x
1,h
1). получаем с учетом того, что 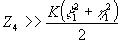 . .
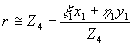 (55) (55)
После подстановки (53) и (55) в (54) и проведения необходимых преобразований получаем:
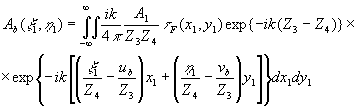 (56) (56)
Для изображения, создаваемого первой восстановленной волной, распределение амплитуд и фаз будет
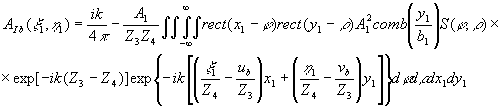 (57) (57)
Это выражение представляет собой преобразование Фурье от свертки двух функций, и, следовательно, используя прямую и обратную теоремы о свертке, перепишем (57), опуская постоянные, коэффициенты,
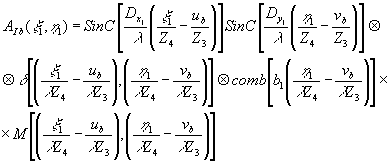 (58) (58)
- 276 -
где
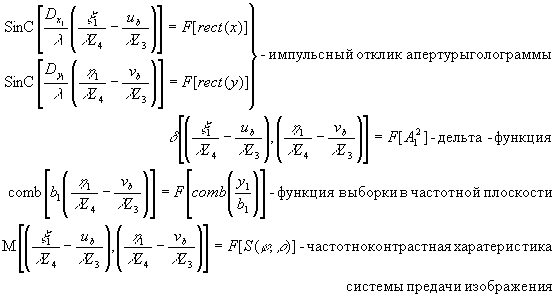
Из свойств дельта-функции следует, что
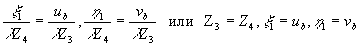 (59) (59)
и при этом получается сфокусированное изображение точечного источника, координаты которого в плоскости восстановленного изображения совпадают с координатами точечного источника восстанавливающей волны. Тогда (58) примет вид;
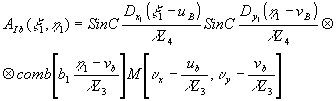 (60) (60)
Изображение, формируемое первой восстановленной волной, представляет собой ряд изображений точечного опорного источника, расположенных по обе стороны от точки (ub,vb) вдоль направления h
1 с периодом 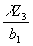 , что обусловлено строчной структурой голограммы. Каждое изображение точечного источника описывается функцией , что обусловлено строчной структурой голограммы. Каждое изображение точечного источника описывается функцией 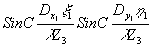 , амплитуда которой ограничивается частотноконтрастной характеристикой системы передачи с началом отсчета в точке (ub,vb) плоскости восстановленного изображения или в точке , амплитуда которой ограничивается частотноконтрастной характеристикой системы передачи с началом отсчета в точке (ub,vb) плоскости восстановленного изображения или в точке 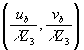 плоскости пространственных плоскости пространственных
- 277 -
частот голограммы.
Аналогичным способом получаем распределение амплитуд в изображении, формируемом второй волной:
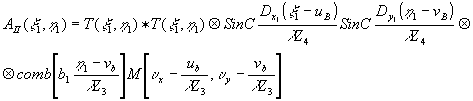 (61) (61)
где t(x
1,h
1)*t(x
1,h
1)=f[|
f(x1,y1)|
2] - функция автокорреляции функции пропускания объекта.
Таким образом, вторая волна формирует ряд изображений функции автокорреляции, совпадающий с предыдущим рядом изображений, причем, яркость этих изображений по мере удаления от точки (ub,vb) уменьшается пропорционально спаду частотноконтрастной характеристики системы передачи, а разрешение в этих изображениях определяется импульсным откликом апертуры голограммы.
Для третьей и четвертой восстановленных волн, которые несут информацию об объекте, получаем следующие распределения амплитуд и фаз в плоскости восстановленного изображения:
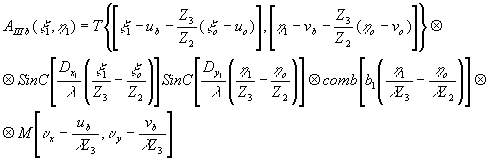 (62) (62)
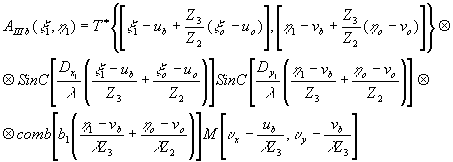 (63) (63)
- 278 -
где
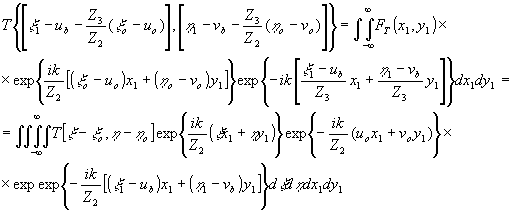 (63) (63)
Условия фокусировки вытекают из равенства показателей экспонент прямого и обратного преобразований Фурье, т.е.
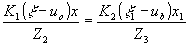
Следовательно, если k1=k2, что выполняется, когда запись и восстановление производится при одной длине волны, то
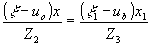
Если х=х1 или 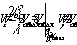 , т.е. голограмма не претерпела масштабных изменений в процессе передачи, то , т.е. голограмма не претерпела масштабных изменений в процессе передачи, то
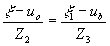
из чего следует, что при восстановлении изображения с голограммы Фурье угловой размер восстановленного изображения, остается постоянным и равным угловому размеру голографируемого объекта, если масштаб голограммы в процессе передачи не изменялся.
Если же 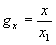 , то , то 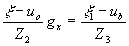
что означает, что угловой размер изображения, восстановленного с голограммы Фурье, претерпевшей изменение масштаба, изменяется обратно пропорционально изменению масштаба.
Третья и четвертая волны формируют пару сопряженных изображений объекта:
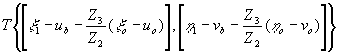
- 279 -
и 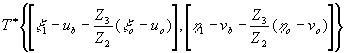
симметричных относительно точки (ub,vb). Наличие в голограмме строчной структуры приводит к тому, что восстановление изображения мультиплицируются, образуя ряд из обращений вдоль направления h
1. Разрешение в восстановленном изображении определяется шириной импульсного отклика апертуры голограммы, а поле зрения, определяющее максимальный размер восстановленного изображения, ограничивается шириной частотно-контрастной характеристики системы передачи, при этом яркость восстановленного изображения спадает по мере удаления координат от изображая точечного опорного источника.
б) Восстановление изображения с голограммы Френеля.
Уравнение голограммы Френеля, переданной по телевизионному тракту, получаем путем подстановки (7) в (51):
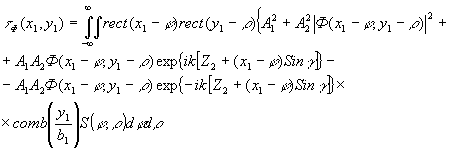 (65) (65)
При освещении этой голограммы волной света, подобной опорной волне, применявшейся при голографировании , получаем за голограммой, как и в предыдущем случае, четыре волны света, из которых только две последних несут полезную информацию об объекте.
Выявить воздействие системы передачи на восстановленное изображение в случае френелевской голограммы сложнее, чем в случае Фурье-голограммы, ибо плоскость пространственных частот голограммы, а, следовательно, и плоскость непосредственного воздействия частотноконтрастной характеристики системы и импульсного отклика апертуры голограммы не совпадает с плоскостью восстановленного изображения. Тем не менее, это возможно.
Рассмотрим распределение амплитуд и фаз в некоторой плоскости, параллельной плоскости голограммы и удаленной от нее на
- 280 -
расстояние, создаваемое каждой из восстановленных волн.
Для первой восстановленной волны с помощью интеграла Кирхгофа получаем;
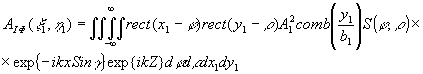 (66) (66)
Используя френелевское приближение, выразим r через координаты голограммы и изображения:
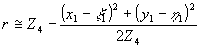 (67) (67)
Подставив (67) в (66) и изменив порядок интегрирования, имеем
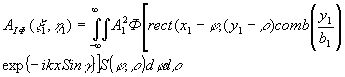 (68) (68)
т.е. в плоскости восстановленного изображения первая волна создает френелевский образ растра переданной голограммы, разрешение в котором определяется разрешающей способностью системы передачи изображения.
Аналогично для второй волны получаем
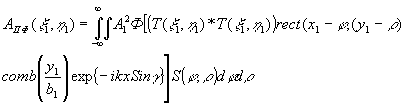 (69) (69)
где 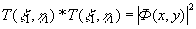
что дает в плоскости изображения френелевский образ функции автокорреляции функций пропускания объекта с наложенным на нее расфокусированным изображением растра. Разрешение по этому изображению также определяется разрешающей способностью системы передачи изображения
Рассмотрим распределения амплитуд, создаваемые двумя последними волнами в плоскости изображения. Перепишем третье слагаемое
- 281 -
уравнения голограммы из выражения (65), применив к подынтегральному выражению прямую и обратную теоремы о свертке:
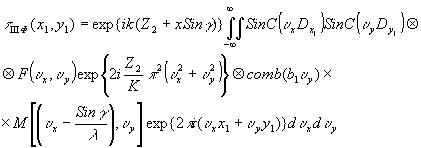 (70) (70)
где 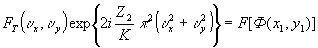
Распределение амплитуды и фазы волны, обусловленной этим слагаемым, в плоскости изображения определяется с помощью интеграла Кирхгофа для случая френелевского приближения:
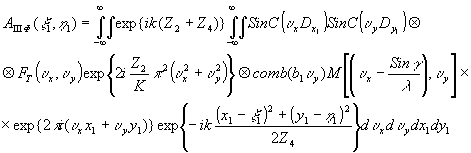 (71) (71)
После интегрирования но dx1 и dy1 получаем
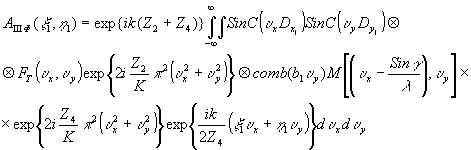 (72) (72)
Из равенства нулю показателей экспонент , содержащих z2 и z4, следует условие фокусировки: +z2=-z4, т.е. изображение объекта восстанавливается на том же самом месте по отношению к голограмме, где помещался голографируемый объект. С учетом этого уравнение (72) принимает вид;
- 282 -
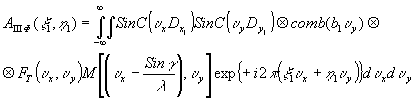 (73) (73)
или после интегрирования
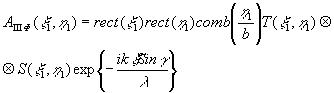 (74) (74)
Из двух форм записи амплитудного распределения (73) и (74) видно, что размеры восстановленного изображения ограничиваются размерами переданной голограммы, разрешение по изображению определяется Частотноконтрастной характеристикой системы передачи, начало отсчета которой сдвинуто относительно нулевой частоты спектра пространственных частот объекта на величину несущей пространственной частоты голограммы, пропорциональную синусу угла падения опорной волны. При этом оказывается, что разрешение вдоль оси u
х оказывается меньше на величину 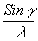 , чем разрешение вдоль оси u
у или чем разрешение, обеспечиваемое системой передачи изображения. , чем разрешение вдоль оси u
у или чем разрешение, обеспечиваемое системой передачи изображения.
Строчная структура переданной голограммы приводит к тому, что на восстановленное изображение как бы накладывается расфокусированное изображение растра. Это равносильно, наблюдению восстановленного изображения через растровую структуру, расположенную в плоскость голограммы. Все это схематически изображено на рис.9.
Для амплитудного распределения в плоскости изображения, формируемого четвертой волной, получаем
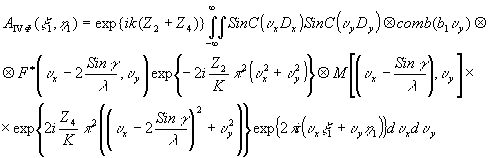 (75) (75)
- 285 -
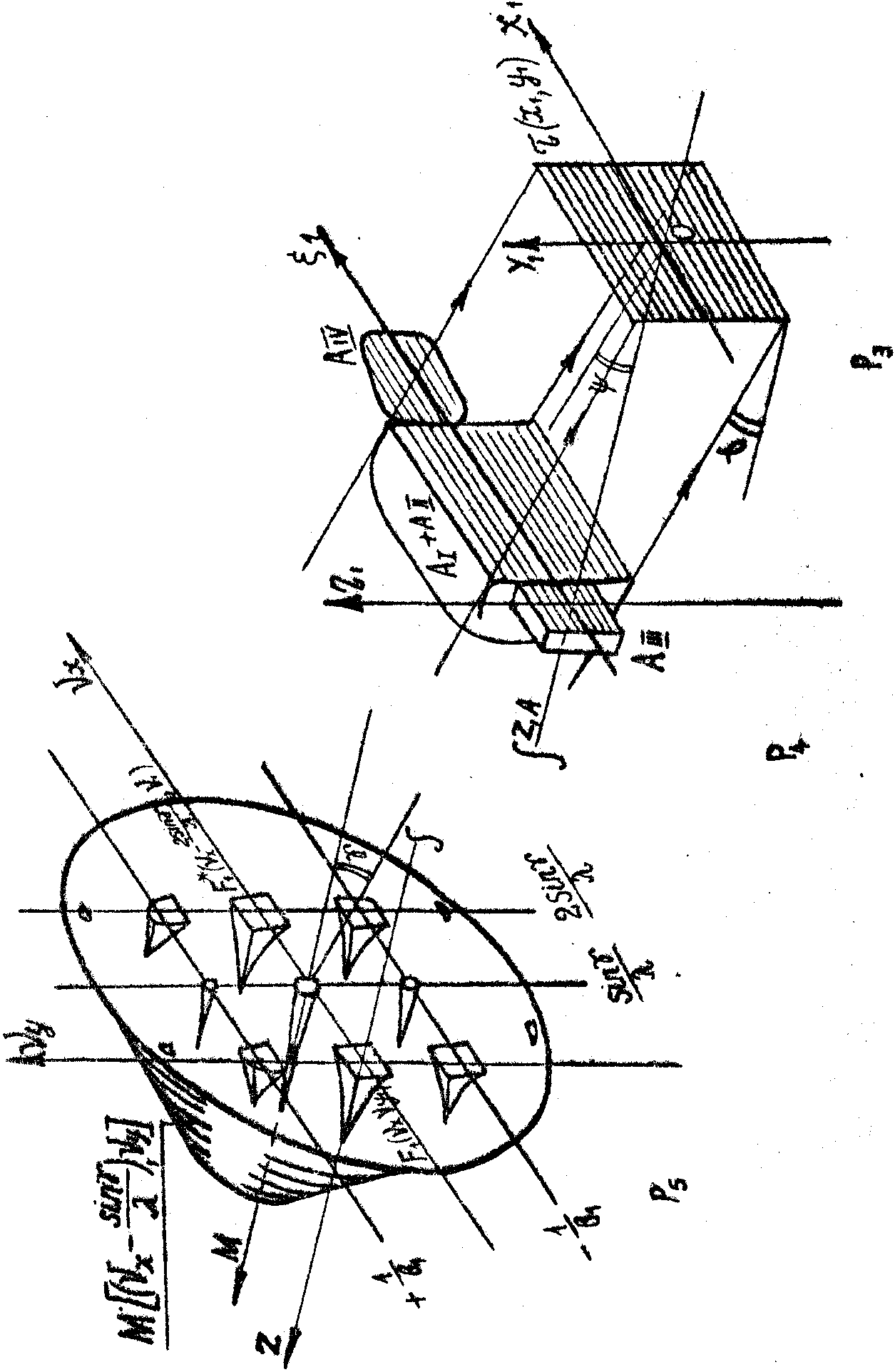
Рис.9. Изображение, восстановленное с переданной френелевской голограммы.
- 284 -
Это выражение показывает, что четвертая волна дает в плоскость мнимого восстановленного изображения, сформированного третьей волной, расфокусированное и искаженное изображение.
Для того, чтобы сформировать это изображение, необходимо освещать голограмму плоской волной сопряженной опорной. Тогда за голограммой перед наблюдателем сформируется неискаженное действительное изображение объекта с теми же ограничениями, накладываемыми системой передачи, что и для случая мнимого изображения.
В заключение отметим, что параметры схемы голографирования (взаимное расположение точечного опорного источника, объекта и плоскости регистрации) определяют вид кодирования информации регистрирующей голограммой, ширину спектра пространственных частот голограммы в характер воздействия системы передачи на изображение, восстановленное с переданной голограммы.
- 285 -
Литература
1. e.n.leith, i.upatnieks, b.b.hildebrand, k.a.haines. j.smpte, 74, № 10, 893-096, 1966. Перевод "Зарубежная радиоэлектроника", № 5, 3-11, 1966.
2. l.h.enloe, j.a.murphy, c.b.rubinstein. the bell system techn.j., v.45, n 2, 335-339, 1966.
Перевод "Зарубежная радиоэлектроника", № 11 , 31-33, 1966.
3. И.С.Клименко, Г.И.Рукман. ЖТФ, т.37, 18, 1532-1534, 1967.
4. С.Б.Гуревич, Г.А.Гаврилов, А.Б.Константинов, В.Б.Константинов, Ю.И.Островский, Д.Ф.Черных. ЖТФ, Т.38, № 3, 513-529, 1968.
5. j.g.vienot, g.perrin. computer rendus, v.267, n 21, b1137-b1140, 1968.
6. Б.П.Константинов, С.Б.Гуревич и др. ЖТФ, т.39, № 2, 347-358, 1969.
7. a.larsen. the bell system techn.j., v.48, 2507-2527, 1969.
Перевод "Зарубежная радиоэлектроника", & q, 24-37, 1970.
8. П.В.Шмаков, Б.Г.Жебель и др. Техника кино и телевидения., № 10, 42-47, 1969.
9. Дж.Гудмен. Введение в Фурье-оптику , Изд-во "Мир", 285, 1970.
10. А.Папулис. Теория систем и преобразований в оптике. Изд-во "Мир", 41, 1971.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

