|
|
 |
 |

|
| |
ГОЛОГРАФИЧЕСКИЕ МЕТОДЫ АМПЛИТУДНО-ФАЗОВЫХ ПРЕОБРАЗОВАНИЙ ЛАЗЕРНЫХ ПУЧКОВ
М.С.Соскин
Описан голографический способ управления волновым Фронтом лазерного излучения. Рассмотрены теоретические соотношения, описывающие преобразование поперечных мод в гауссов пучок с плоским волновым фронтом, которые находятся в хорошем согласии с результатами для гелий-неонового лазера. Анализируется возможность динамической коррекции лазерных фронтов с помощью фототропных растворов и нелинейных кристаллов.
1. В большинстве случаев научного и практического использования лазеров к пространственно-угловой структуре лазерных пучков предъявляются разнообразные и довольно жесткие требования. Так, для целей передачи энергии, связи, локации, фокусировки пучков в малую область необходимы гауссовы пучки с плоским фронтом. В ряде физических и технологических применений лазеров, в том числе в голографии, необходимы пучки с максимально однородным амплитудным распределением в заданном сечении. Для целей оптической обработки информации надо уметь получать систему гауссовых пучков в т.д.
Излучение лазеров, как правило, не отвечает этим требованиям в силу многомодовости генерации и отступления волновых фронтов отдельных мод от идеальной формы, особенно для твердотельных и жидкостных лазеров. Поэтому актуальна задача разработки методов коррекции и преобразования когерентных пучков с произвольным волновым фронтом к заданному амплитудно-фазовому распределению.
Использование линз , телескопов и других оптических систем для этой цели неэффективно, так как они могут лишь менять общую
- 232 -
кривизну либо пространственно-угловой масштаб волнового фронта, не устраняя его нерегулярностей. Не годится и применение различных селектирующих систем, действующих путем разложения исходного пучка, так как при этом неизбежны значительные потери. Очевидно, что необходима разработка методов преобразования пучков, в принципе, без потерь. Следствием этого должно быть существенное увеличение соевой яркости излучения реальных лазеров.
Ранее нами был предложен метод преобразования пучков с произвольным фронтом, основанный на принципах голографии /1,2/ Пусть I и II - два когерентных пучка с распределением А×
еij
и B×
еiy
в плоскости голограммы. Тогда на ней записывается интерференционная картина
|
А×
еij
+B ×
еij
|
2 = |
А2+B 2|
+ А×
B×
еi(j
-y
)+ А×
B×
еi(y
-j
) (1)
Если теперь голограмму обработать, установить на прежнее место и направить на нее один из исходных пучков, например I, то непосредственно за голограммой возникнет поле:
А(А 2+B 2)e ij
+ А2B ×
еi(2j
-y
)+ А2B ×
еiy
(2)
Здесь первый, второй и третий члены описывают, соответственно, нулевой, (-1)-й и (+1)-й порядки дифракции. Главный интерес представляет (-1)-й порядок. Как видно, он описывает преобразование
А×
е ij
®
А А2B ×
еiy
(3)
т.е. полную смену фазового фронта пучка I, независимо от его сложности и нерегулярности. Из этого результата и вытекает предложенная схема голографического преобразования пучков. Из части исходного пучка (I) путем отщепления и оптических преобразований создается пучок с заданным фронтом (II) (ср./3/). Картина интерференции записывается на голограмме, убираются элементы для формирования вспомогательного пучка а на голограмму, установленную на прежнее место, направляется пучок I, который в (-1)-м порядке преобразуется, согласно (3). Окончательно необходимое распределение получают с помощью Фурье-преобразования (для дальней
- 233 -
зоны) либо обратного Фурье-преобразования (для ближней зоны).
В зависимости от задачи преобразование фронта можно осуществлять как в ближней, так и в дальней зонах. Преобразование в ближней зоне (рис.1) применяют , когда необходимо получение пучков с максимальной осевой яркостью. Линза Л переносит в плоскость Р1 голограммы Г распределение исходного пучка в ближней зоне. Делительное устройство К отцепляет часть пучка I, которая трансформируется в заданный пучок II с помощью оптической системы Т (телескоп с диафрагмой в случае получения гауссова пучка). Выходная линза Л телескопа переносит в Р1 ближнюю зону пучка II.
На рис.1б показана схема второго этапа преобразования. Голограмма для удобства помещена непосредственно в плоскость ближней зоны Р. Порядок (-1), совпадающий по направлению с пучком II, обладает нужным фазовым фронтом. На рис.1в в качестве примера показано преобразование дальней зоны моды ТЕМ04, в результате которого основная доля энергии сосредоточена в центральном максимуме.
Пру необходимости преобразования распределения пучка в ближней зоне на голограмме записывается интерференция с II дальней зоны пучка I (рис.2а). Исправленную ближнюю зону получают с помощью обратного Фурье-преобразования (рис.26). На рис.2в показано преобразование ближней зоны моды ТЕМ11.
Любопытными , практически важными свойствами обладает и дифракционный порядок (+1). Согласно (2), он имеет фазовый фронт (2j
-y
). Ясно, что для сложного волнового фронта в этом порядке нерегулярности будут удваиваться. Однако при использовании резонаторов со сферическими зеркалами фазовые неоднородности малы даже для твердотельных лазеров (см., например./4/). В этом случае главный вклад в расходимость дают регулярные скачки фазы на p
между модовыми пятнами. Но тогда удвоение фазы ведет к устранению этих скачков. Поэтому расходимость порядка (+1) оказывается такой же, как и (-1)-го, если исключить общую кривизну поля, задаваемую зеркалами и одинаковую для всех мод.
Указанная особенность (+1)-го порядка реализуется не только в голографических, схемах, но и при нелинейном преобразовании с четным умножением частоты излучения. Это было экспериментально показано при генерации второй гармоники излучения гелий-неонового
- 234 -
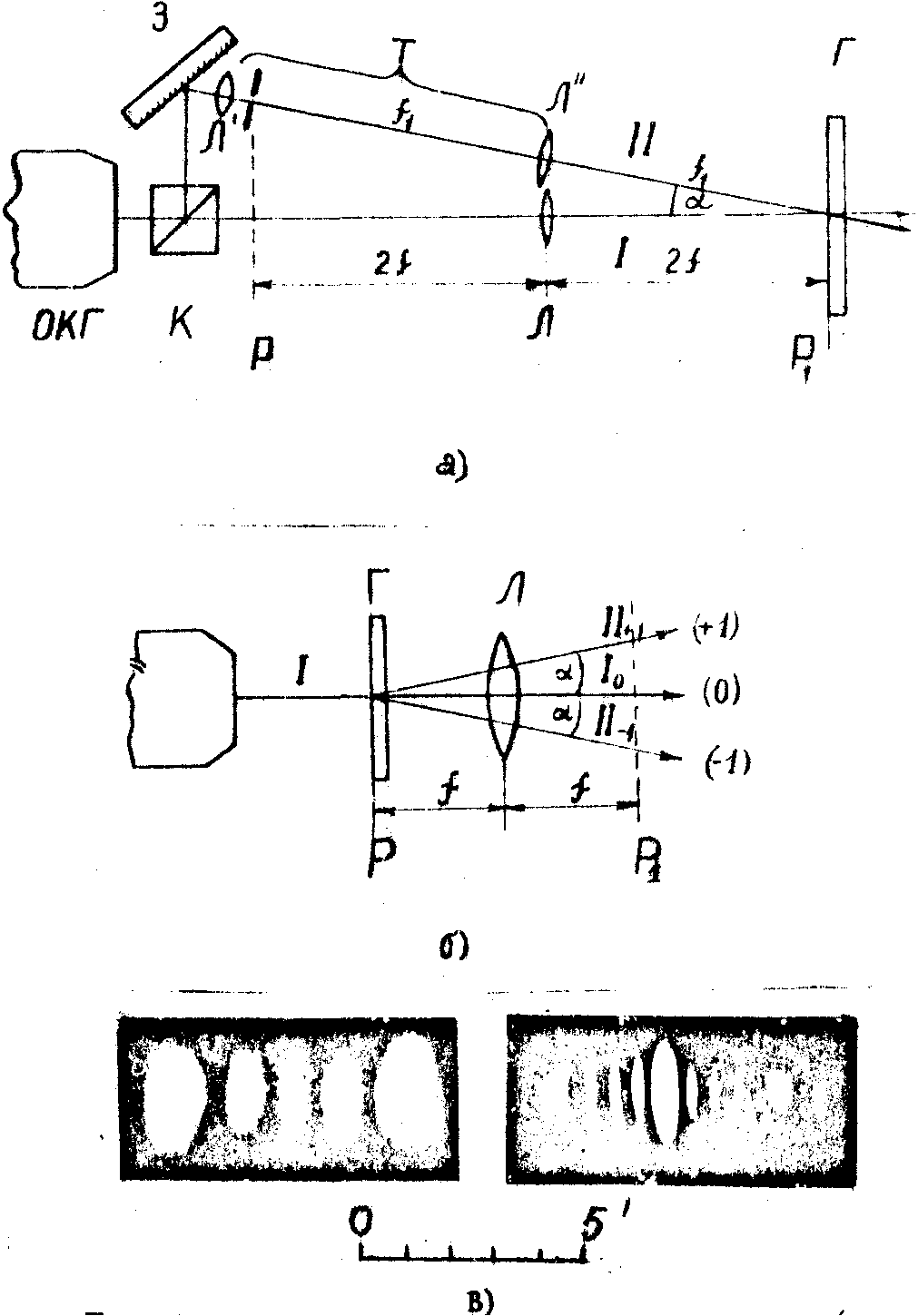
Рис.1 . Преобразование углового распределения (дальней зоны) волнового фронта.
а) схема получения голограммы-корректора; ¦
и ¦
1 - фокусные расстояния линз Л и Л"; З - поворотное зеркало; a
- угол между пучками I и II;
б) схема преобразования пучка; ¦
- фокусное расстояние линзы Л; Р 1 - плоскость дальней зоны; (+1),(0),(-1) - порядки интерференции.
в) дальняя зона моды ТЕМ 04 до (слева) и после (справа) преобразования.
- 235 -
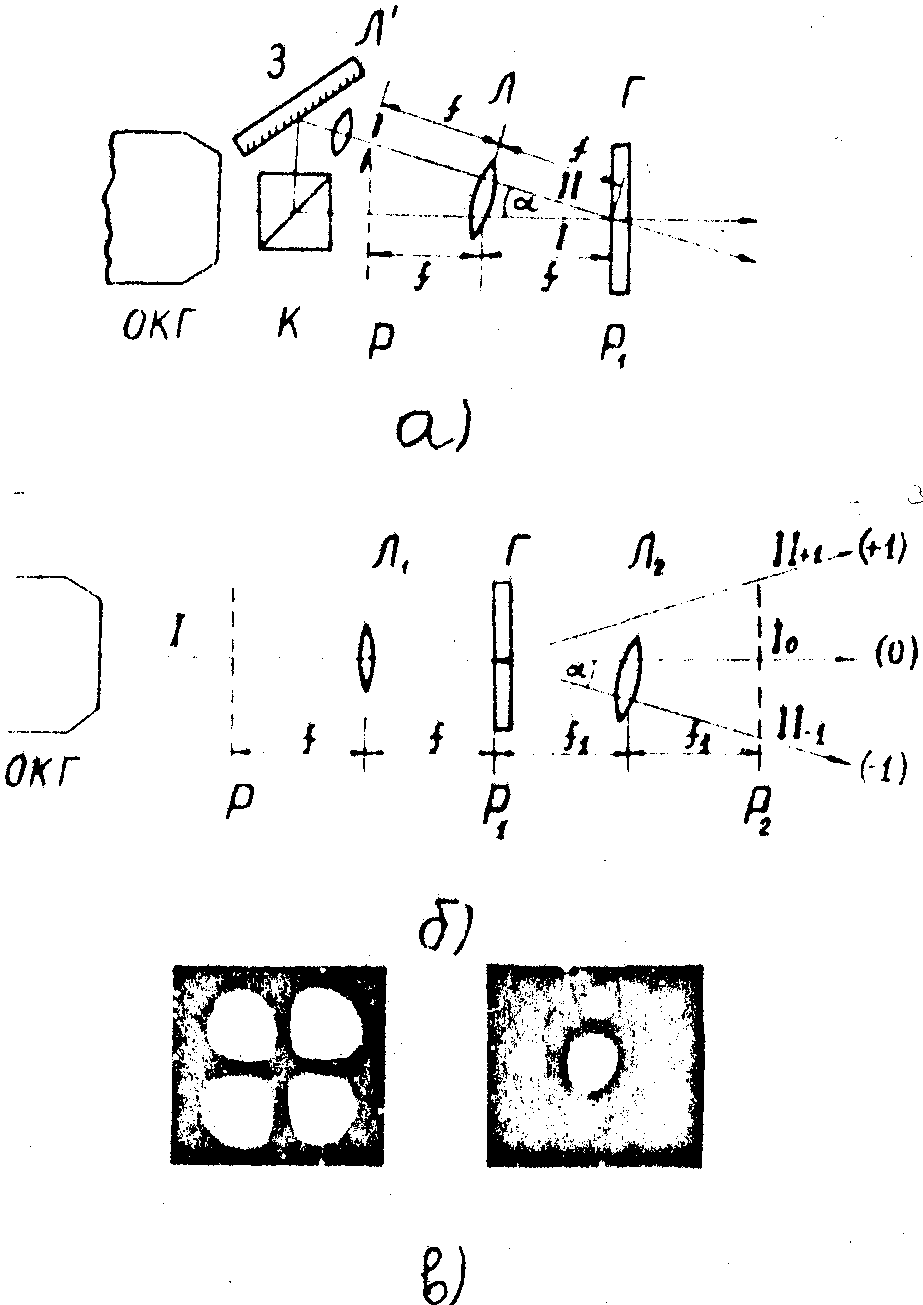
Рис.2. Преобразование пространственного (ближняя зона) распределения волнового фронта.
а) схема получения голограммы-корректора; ¦
- фокусное расстояние линзы Л; З - поворотное зеркало; Г - голограмма; Т - телескоп; a
- угол между пучками I и II;
б) схема преобразования пучка; ¦
и ¦
1 фокусные расстояния линз Л1 и Л2; Р и Р2 плоскости ближней зоны; (+1),(0),(-1) - порядки интерференции;
в) ближняя зона моды ТЕМ 11 до (слева) и после (справа) преобразования.
- 236 -
лазера с l
=1.15 мкм в кристалле КДР /5/.
Нулевой порядок сохраняет исходный волновой фронт, его наличие лишь снижает эффективность преобразования. Для подавления нулевого порядка можно либо использовать объемную голограмму при соблюдении угла Брэгга /6/ либо применять решетку-эшелетту с несимметричным профилем штриха,
В заключение общего анализа отметим, что голограмма-корректор может выполнять одновременно и обычные оптические операции с преобразованным пучком (фокусировку и др.). если сформировать соответствующий фронт у пучка II при получении голограммы.
2. В качестве типичного примера преобразования лазерных пучков рассмотрим задачу трансформации мод высоких поперечных индексов конфокального резонатора в гауссов пучок с плоским фазовым фронтом. Начнем с теоретического анализа. Распределение амплитуды и фазы поля в ближней зоне одномерного конфокального резонатора с точностью до общей кривизны волнового фронта описывается функциями Эрмита /7/:
um(t) = Hm(t)exp(-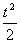 ) (4) ) (4)
где 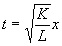 , , 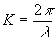 - волновой вектор, L - радиус кривизны зеркал, Hm(t) - полиномы Эрмита. Предполагается, что размеры зеркал существенно больше области локализации поля. - волновой вектор, L - радиус кривизны зеркал, Hm(t) - полиномы Эрмита. Предполагается, что размеры зеркал существенно больше области локализации поля.
Если фазовый фронт пучка II плоский, то в ближней зоне преобразованное поле (-1)-го порядка становится синфазным, а распределение амплитуды в предположении линейности записи голограммы оказывается пропорциональным квадрату амплитуды исходного пучка в соответствии с (3).
Для нахождения углового распределения преобразованного излучения удобно поле в ближней зоне представить суммой гауссовых функций /8/:
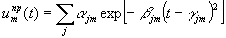 (5) (5)
Здесь a
jm, b
-1jm и g
jm- амплитуды, дисперсии и положения максимумов гауссовых функций.
Тогда поле в дальней зоне определяется Фурье-преобразованием
- 237 -
функций (5):
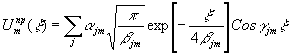 (6) (6)
где 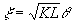 . Проще всего все указанные операции um®
uпрm® . Проще всего все указанные операции um®
uпрm®
U прm, особенно для сложных распределений, делать графически.
Распределение поля в дальней зоне после преобразования для первых пяти типов колебаний показано на рис.3. Как видно, независимо от исходной структуры моды, в частности, для нечетных мод с минимумом поля вдоль оси резонатора, волновой фронт после коррекции имеет сходное распределение. Главный максимум автокорреляционной функции направлен вдоль оси резонатора. (Как было показано на
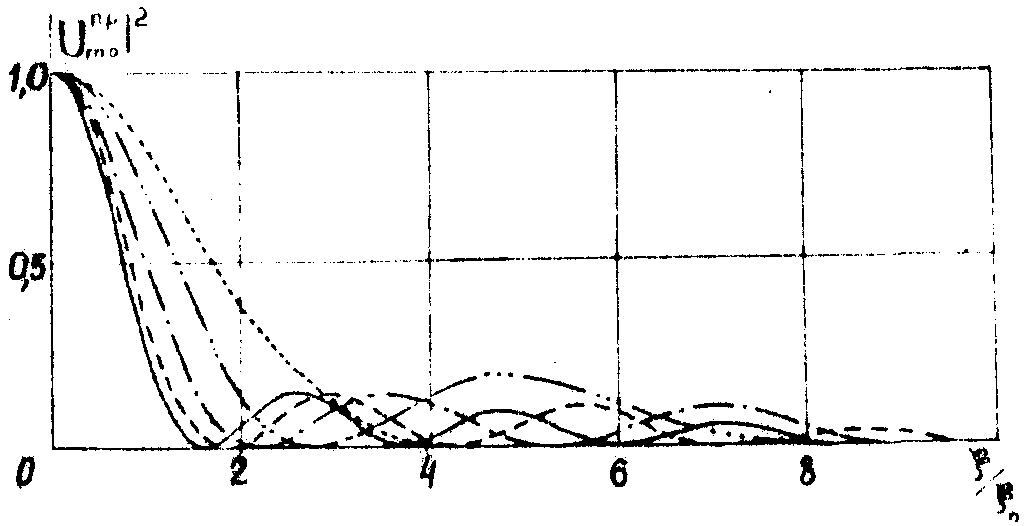
Рис.3. Теоретически рассчитанное угловое распределение энергии для мод TEM0m.
··· m=0, —···- m=1, —·— m=2, - - — m=3, — m=4.
примере моды TEM02 /9/, в нем сосредоточено до 80% всей энергии). Кроме того, имеются на порядок более слабые побочные максимумы, число которых равно удвоенному поперечному индексу. Их устранение приводит к окончательному преобразованию излучения в гауссов пучок не только в дальней, но и в ближней зоне /9/.
Рассмотрим соотношения, которые описывают изменение осевой яркости при голографической коррекции. Количественной характеристикой
- 238 -
осевой яркости пучка с заданным угловым распределением энергии W(q
) служит угловая зависимость доли энергии, излучаемой в заданный телесный угол 2q
: 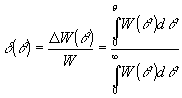 . Поскольку гауссово распределение поля получают, работая в режиме моды TEM00, разумно в качестве меры повышения осевой яркости излучения моды TEMmn взять величину . Поскольку гауссово распределение поля получают, работая в режиме моды TEM00, разумно в качестве меры повышения осевой яркости излучения моды TEMmn взять величину
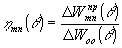 (7) (7)
которую в дальнейшем будем называть яркостным коэффициентом преобразования. Здесь D
Wпрmn( q
) относится к моде TEMmn после преобразования.
Преобразуем (7) к величинам, определяемым свойствами генерации и голограммы. Пусть дифракционная эффективность голограммы
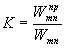 (8) (8)
Тогда легко показать, что если
Wmn = xmn·Woo (9)
то
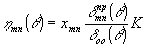 (10) (10)
Проанализируем полученное выражение для рассматриваемого случая конфокального резонатора. У нижайших поперечных мод дифракционные потери много меньше потерь на излучение. Поэтому можно считать, что изменение выходной мощности связано главным образом с изменением объема генерации. Как известно /10/, шейка каустики моды возрастает примерно как 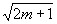 . Аналогичную или близкую зависимость должна иметь и выходная мощность генерации. . Аналогичную или близкую зависимость должна иметь и выходная мощность генерации.
Ход 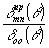 легко найти из кривых рис.3. Видно, что ширина главного максимума, быстро насыщается с ростом индекса моды m. Следовательно, легко найти из кривых рис.3. Видно, что ширина главного максимума, быстро насыщается с ростом индекса моды m. Следовательно, 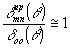 Эта зависимость имеет простое физическое объяснение, будем рассматривать ближнюю зону как поле в плоскости квази еской решетки. Тогда угловая Эта зависимость имеет простое физическое объяснение, будем рассматривать ближнюю зону как поле в плоскости квази еской решетки. Тогда угловая
- 239 -
ширина главного максимума интенсивности определяется направлением на первый дифракционный минимум 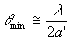 , где 2а' - область генерации. Отсюда ясно, что с ростом поперечных индексов моды расходимость центрального максимума медленно растет, стремясь к , где 2а' - область генерации. Отсюда ясно, что с ростом поперечных индексов моды расходимость центрального максимума медленно растет, стремясь к 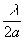 , где 2а - ширина зеркал. , где 2а - ширина зеркал.
Итак, для конфокального резонатора осевая яркость преобразованного пучка растет с индексом моду как
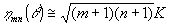 (11) (11)
Можно полагать, что этот результат имеет более широкую область применимости, так как и в других типах резонаторов без специальной селекции угловых мод их пороги генерации близки.
Из (II) следует, что голографическое преобразование становится энергетически выгодным уже при K³
[(m+1)(n+1)]-1. Для моды TEM44 это дает K³
20%, что довольно легко реализуется на эксперименте /9/.
3. Экспериментальное осуществление коррекции проводилось по схеме рис.1, которая собиралась на оптической скамье OСK-3. Использовался гелий-неоновый лазер ЛГ-75 (l
=6328Å). Устойчивая генерация на изолированных поперечных модах достигалась с помощью малых разъюстировок резонатора. Для создания опорного пучка II применялись частично отражающее зеркало и телескоп с диафрагмой, которая вырезала одно из модовых пятен. Увеличение телескопа подбиралось таким, чтобы расширенный пучок II на голограмме полностью покрывал исходный пучок I.
Угол интерференции a
=2¸
5°, что позволяло использовать фотоматериалы с разрешающей способностью до 300 штр/мм. Фотопленка обрабатывалась стандартным проявителем Д-19 и кислым фиксажем. Для повышения дифракционной эффективности преобразования голограмма отбеливалась 1.5-процентным раствором красной кровяной соли. Восстановление положения голограммы на стадии реконструкции обеспечивалось специальным держателем.
Типичные картины поля при коррекции в ближней и дальней зонах показаны на рис.4. Для количественного сопоставления с теорией определялось распределение энергии излучения в дальней зоне после коррекции в ближней зоне для поперечных мод TEM0m при m=1¸
4
- 240 -
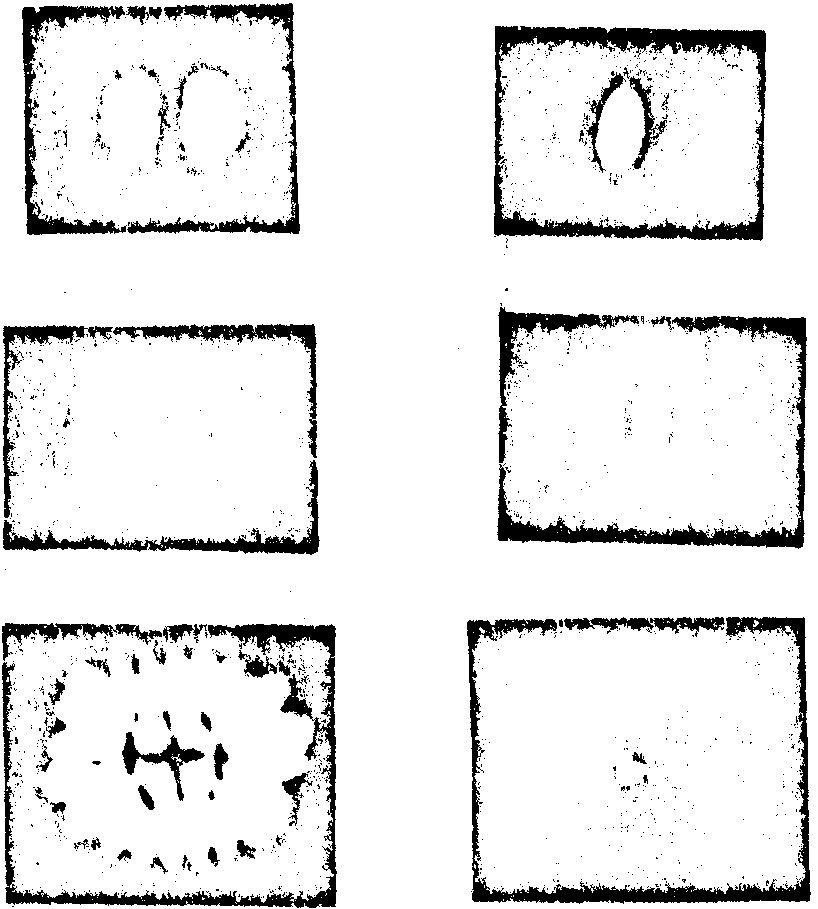
Рио.4. Дальние зоны мод TEM01, TEM02 и сложной поперечной моды высоких индексов до (слева) и после (справа) коррекции формы волнового фронта.
(рис.5), сопоставление рис.3 и 5 показывает полное соответствие экспериментально подученных кривых с рассчитанными. Некоторая асимметрия в относительной высоте и ширине побочных максимумов может быть связана с различной дифракционной эффективностью участков голограммы, относящихся к разный пятнам моды.
В соответствии с теорией доля энергии, идущей в центральный максимум, мало зависит от индекса моды и составляет 70-80% общей анергии преобразованного пучка. При К=1 это и будет пределом полной эффективности преобразования, если гауссов пучок получать диафрагмированном побочных максимумов */.
*/ Потери, связанные с устранением побочных максимумов, не являются неизбежными. Близкое к гауссовому распределение можно получить при использовании в дальней зоне вместо диафрагмы специально подобранного фазового фильтра. Другой путь - задание амплитудного фронта пучка II на голограмме (см.(3)).
- 241 -
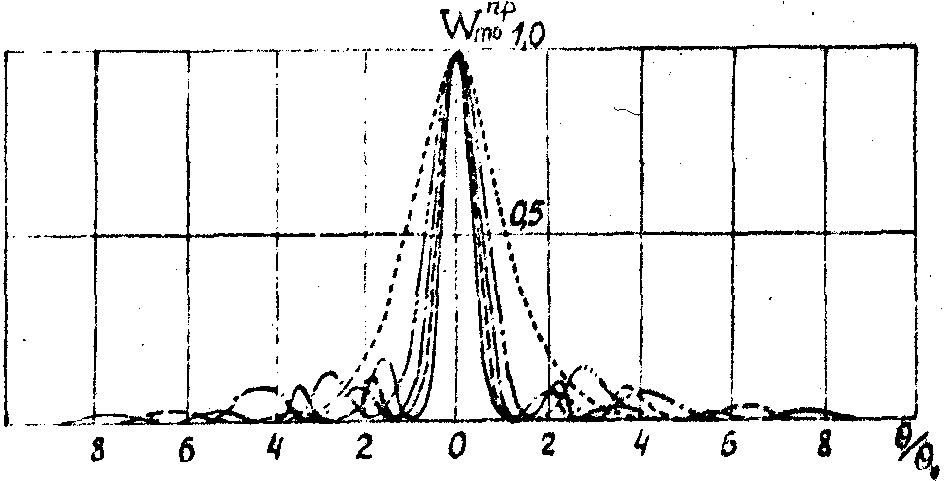
Рис.5. Экспериментально определенное угловое распределение анергии для мод TEM0m.
··· m=0, —···— m=1, —·— m=2, — — — m=3, — m=4.
Следует отметить, что в некоторых случаях наличие побочных максимумов в дальней зоне может оказаться полезным. В ряде физических и технических задач возникает необходимость получить не гауссово, а например, прямоугольное распределение амплитуды поля. Это легко осуществить с помощью комбинированных амплитудно-фазовых фильтров в дальней зоне, параметра которых лучше всего вычислить с помощью ЭВМ .
Экспериментально проверялась и зависимость выходной мощности от индекса поперечной моды. В согласии с теорией для m=1,2,3,4 в результате большого числа циклов измерений были получены следующие средние значения x0m: 1.65; 2.2; 2.6 и 3.2, соответственно.
Полученная экспериментальная зависимость яркостного коэффициента преобразования h
0m показана на рис.6. Как видно, для заданной моды h
слабо зависит от угла, достигая минимума при q
=q
о расходимости моды TEM00. С ростом m увеличивается h
(q
о) примерно как 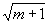 (ср. (11)). (ср. (11)).
Таким образом, теория хорошо описывает все характеристики преобразованного лазерного излучения для случая газового лазера и чистых поперечных мод при использовании фазовых голограмм на отбеленных фотоматериалах. Следующая актуальная задача - использование
- 242 -
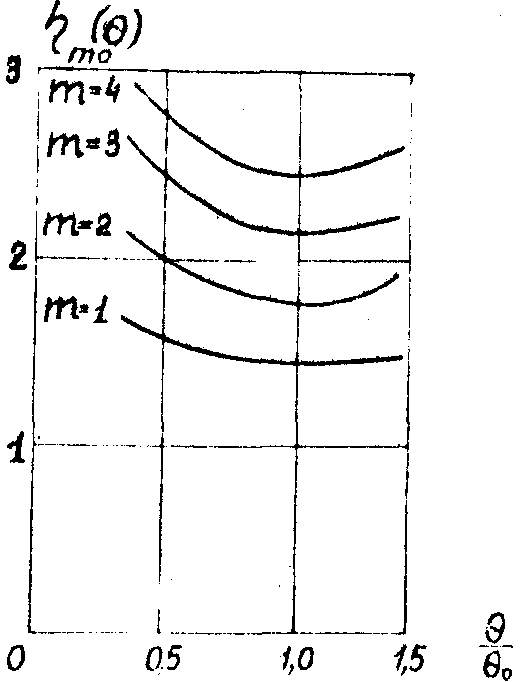
Рис.6. Угловая зависимость яркостного коэффициента преобразования.
процессов динамической голографии на различных нелинейных средах для коррекции излучения импульсных лазеров в процессе генерации.
4. Общая идея создания динамической голограммы на нефотографических средах достаточно проста. Необходимо, чтобы поле, несущее информацию, вызывало достаточно быстрое локальное изменение оптических свойств среды, зависящее от интенсивности поля. Тогда будет образовываться решетка, повторяющая структуру интерференционного поля. Изменение коэффициента поглощения создает амплитудную решетку, показателя преломления - фазовую. Если период решетки мал по сравнению с ее толщиной (более строгий критерий смотри в /6/), то решетка будет обладать объемными свойствами, т.е. при соблюдении угла Вульфа-Брэгга остается лишь (-1)-й порядок дифракции.
Теоретический анализ /6/ показывает, что максимальная эффективность амплитудной объемной решетки не может превысить 3.7% при работе на пропускание и 7.2% при работе на отражение. Этого явно недостаточно для целей эффективного исправления волнового фронта.
- 243 -
Фазовая объемная решетка позволяет осуществить 100%-ное преобразование пучков при работе под углом Вульфа-Брэгга */. Поэтому нас будут интересовать процессы, приводящие в конечном итоге к локальному изменению показателя преломления. Как было показано ранее, пространственные частоты, необходимые для исправления пучков, невелики, что позволяет ограничиться периодами решетки порядка нескольких микрометров. Это обстоятельство является благоприятным, так как на практике эффективность преобразования обычно падает при малых периодах решетки.
Требуемый диапазон времени образования и стирания динамических решеток чрезвычайно широк. Так, для лазеров непрерывного действия - это секунды и минуты, для лазеров с большой частотой повторения вспышек – 10-2 сек, импульсных лазеров в режиме свободной генерации – 10-6 сек, в режиме модуляции добротности – 10-9 сек.
Один из наиболее изученных процессов образования динамической голограммы - изменение показателя преломления среды за счет тепловыделения при поглощении света /11-13/. Было показано, что при помещении в интерференционное поле линейно или нелинейно поглощающих сред образуется фазовая решетка, время жизни t
которой определяется теплофизическими свойствами среды /13/.
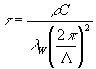 (12) (12)
Здесь r
- плотность среды, С - теплоемкость, l
W - коэффициент теплопроводности и L
- период решетки.
Были исследованы временные характеристики динамической решетки, образованной за счет тепловыделения в растворе криптоцианина в спирте (толщина слоя 0.2 мм, что при углах интерференции ~3° соответствовало условию объемной голограммы). Использовался рубиновый лазер в режиме свободной генерации на одном типе поперечных мод (средняя плотность мощности интерферирующих пучков ~103 вт/см). Начальная прозрачность кюветы на длине волны генерации составляла ~40%.
*/ Отметим, что это условие автоматически соблюдается в описанных выше схемах.
- 244 -
В соответствии с ( 12) при указанных условиях t
@
10-4 сек, т.е. решетка не должна существенно изменяться за интервал между пичками –10-5 сек и реагировать на среднюю мощность генерации. Опыт подтвердил расчет, причем, была достигнута дифракционная эффективность свыше 10%, что свидетельствует о фазовом характере решетки. Типичная картина временной зависимости эффективности преобразования показана на рис.7. Видно, что вначале эффективность дифракции нарастает в согласии с (12). Однако примерно через 150 мксек после начала генерации эффективность дифракции резко спадает до очень малой величины.
Наблюденный эффект очень напоминает изученный нами ранее эффект автосрыва генерации рубинового СКГ в пичковом режиме при внесении в резонатор прозрачных сред /14/. Можно полагать, что и в данном случае тепловыделение за короткое время отдельного пичка (10 -6 сек) приводит к возникновению звуковых волн и микроконвективных процессов, которые должны разрушать регулярную фазовую решетку. Это, по-видимому, ограничивает применение динамических голограмм временами, меньшими ~10-4 сек.
Интересные возможности открывает использование эффекта наведения локальных оптических неоднородностей под действием лазерных пучков в прозрачных нелинейных кристаллах /15/. Было показано, что он весьма перспективен для записи объемных голограмм. Так, при записи интерференционной картины с помощью аргонового лазера (l
=4880 Å) ñ плотностью мощности 1 вт/см2 в кристалле ниобата лития записывалась решетка с эффективностью ~40%, а изображение считывалось гелий-неоновым лазером (l
= 6328Å) малой мощности /16/.
Механизм явления еще не выяснен до конца, однако ясно, что возникновение изменений показателя преломления связано с наличием примесных или дефектных состояний решетки /17/. Пол действием света подходящей длины волны электроны из этих состояний забрасываются в зону проводимости, что приводит к возникновению эффективного поля. Под действием этого поля электроны уходят в менее освещенные области кристалла, где захватываются свободными примесными или дефектными состояниями. Возникшее поле приводит за счет электрооптического эффекта к изменению показателя преломления. Период
- 245 -

Рис. 7. Эволюция фазовой пространственной решетки (раствор криптоцианина в спирте).
1 - записывающий пучок рубинового лазера,
2 - дифрагированный пучок (+1) порядка.
решетки может быть менее 1 мкм /18/.
Были проведены предварительные исследования возможности использования описанного эффекта для преобразования лазерных пучков. Оказалось, что решетка может быть записана и при интерференции сфокусированных пучков гелий-неонового лазера ЛГ-36. Считывание производилось одним из интерферирующих пучков, что соответствовало условиям преобразования пучков. Решетка оказалась объемной, что проявилось в отсутствии всех дифракционных порядков, кроме (-1)-го. Эффективность преобразования составляла несколько процентов и сильно зависела от оптической однородности использованного участка образца и качества обработка его поверхности. Время образования решетки составляло десятки секунд. Можно полагать, что решетки на описанном механизме будут эффективными для лазеров непрерывного действия, а возможно и импульсных при создании соответствующих условий.
Резюмируя этот раздел, можно оказать, что в настоящее время актуально широкое исследование различных механизмов создания и использования динамических голограмм.
В заключение отметим, что голограмма-корректор может быть
- 246 -
использована и как элемент дисперсионного резонатора /19/, одновременно управляющий пространственно-угловыми и спектральными характеристиками генерации лазеров.
Литература
1. М.С.Соскин, М.Д.Бондаренко, А.В.Гнатовский. Укр.физ.журнал, 14, 2, 301 (1969).
2. М.Д.Бондаренко, А.В.Гнатовский, М.С.Соскин. ДАН СССР, 187, 3, 538 (1969).
3. Holography State of the Art Review. 1969. 0ptosonic Press P.96 (1969).
4. В.В.Хоробкин, А.М.Леонтович. ЖЭТФ, 49, 1, 10 (1965).
5. А.В.Гнатовский, М.С.Соскин. Укр.физ.жур., 17, 6, 985 (1972).
6. H.W.Kogelnik. Bell Syst.Techn.Journal, 48, 10, 2909 (1969).
7. Дж.Бойд, Дж.Гордон. Лазеры. М., ИЛ, стр.363, 1963.
8. М.Д.Бондаренко, А.В.Гнатовский, М.С.Соскин. Укр.физ.журнал, 16, 4, 529 (1971).
9. М.С.Соскин, М.Д.Бондаренко. А.В.Гнатовский. Письма ЖЭТФ, 14, 1, 27 (1971).
10. А.М.Леонтович, А.П.Ведута. ЖЭТФ, 46, 1, 71 (1964).
11. H.Eichler, B.Kluzowski. Zs.Angew.Physik, 27, 1, 4 (1969)
12. H.Eichler, P.Glozbach. B.Kluzowski. Zs.Anrew.Physik, 28, 6, 303 (1970).
13. H.Eichler, G.Enterlein, J.Munshau, H.Stahl. Zs.Angew.Physik, 31, 1, 1 (1971).
14. Е.Н.Салькова, М.С.Соскин, П.П.Погорецкий. Сб. "Квантовая электроника", вып.3, Киев, "Наукова думка", стр.3, 1969.
15., A.Ashkin, G.D.Boyd, J.M.Dziedzic, R.G.Smith, А,А.Ваllmann, J.J.Levenstein, K.Nassau. Appl.Phys.Lett., 9, 1, 72 (1966).
16. F.S.Cheu, J.T.La Machia, D.B.Fraser. Appl.Phys.Lett., 13, 7, 223 (1968)
17. W.D.Johnston. J.Appl.Phys., 41, 8, 3279 (1970).
18. R.L.Townsend, J.T.La Machia. J.Appl.Phys., 41, 13, 5188 (1970).
19. М.С.Соскин, В.И.Кравченко, О.Н.Погорелый, Н.Ф.Прокопюк. Укр.физ.журнал, 13, 1, 28 (1968).
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

