|
|
 |
 |

|
| |
ГЕОГРАФИЧЕСКАЯ СПЕКТРОСКОПИЯ
Б.Г.Турухано, Н.Турухано
Рассмотрены основные вопросы Фурье и Френелевской спектроскопии. Приведены конкретные примеры источников, спектральные распределения которых получены методом голографической спектроскопии. Даются критерии разрешающей способности голографических спектрометров.
Введение
Голографическая спектроскопия позволяет исследовать параметры источников излучения: спектральный состав, ширину спектральных линий и их относительную интенсивность в спектре источника. Применение голографического метода помогает упростить сам процесс исследования: получить без применения сложных расчетов на ЭВМ спектр источника, увеличить светосилу записи спектра и т.п.
Покажем, каким образом голограмма связывает спектральные характеристики источника излучения. Рассмотрим простейшую голограмму Френеля, выполненную в параллельных лучах. Пусть на фотопластинку падают симметрично две плоские световые волны с длиной волны l
под углом ±
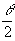 к нормали. В этом случае выражение для интенсивности световой волны, записываемой голограммой можно представить в виде к нормали. В этом случае выражение для интенсивности световой волны, записываемой голограммой можно представить в виде
I = I0{1+Cos[(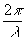 )2Sin( )2Sin(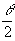 )x]} (1) )x]} (1)
т.е. на фотопластинке образуется дифракционная решетка с частотой
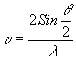 (2) (2)
- 198 -
Если выразить l
через частоту световой волны u
1 и обозначить 2Sin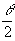 =а, получим =а, получим
u
= a×
u
1 (3)
т.е. пространственная частота голограммы однозначно определяется временной частотой волны, т.е. измеряя частоту полученной дифракционной решетки на голограмме Френеля , можно определить спектральные характеристика источника.
Если источник содержит ряд дискретных линий, то образуется соответствующее число дифракционных решеток различных пространственных частот. Если такую голограмму с набором решеток поместить в переднюй фокальную плоскость линзы и осветить коллимированным лазерным пучком , то в задней фокальной плоскости линзы получим ряд точек, отвечающих спектру источника. В этом случае линза будет производить Фурье-преобразование пространственных частот голограммы, давая непосредственно спектр источника. Этот метод получил название Фурье-спектроскопии и был предложен Строуком в работе /1/.
Для разрешения близких спектральных линий эффективнее использовать метод биений, образующихся от ближних пространственных частот голограммы Френеля. Метод биений позволяет производить интерференционное сравнение некогерентных спектральных линий и в ряде приложений позволяет увеличить разрешение по сравнению с методом Фурье-спектроскопии. Метод биений предложен в работе /2/.
Рассмотрим подробнее оба метода и их приложения к определению спектральной структуры источников излучения.
1. Голографическая спектроскопия Фурье
Метод Фурье-спектроскопии восходит к работам Майкельсона. В 50-х года он получает современную трактовку в работах /3-6/. Развитие Фурье-спектроскопии стало возможно в силу появления быстродействующих вычислительных машин, осуществляющих преобразование Фурье. Подробный анализ интерференционных методов, спектрального анализа с применением преобразования Фурье сделан в работе Паршина /7/.
Дальнейший прогресс Фурье-спектроскопия получила в работах
- 199 -
Строука /1,8,9/ , который применил метод голографии при записи интерферограммы. Для этой цели использовался интерферометр Майкельсона (рис.1). Одно из зеркал - 5 интерферометра наклонялось под углом в к оптической оси. Наклон зеркала на небольшой угол q
давал на фотопластинке полосы равной толщины с частотой 3О линий/мм. Исследовался источник - ртутная лампа. Диффузный рассеиватель - 2 создавал равномерное освещение.
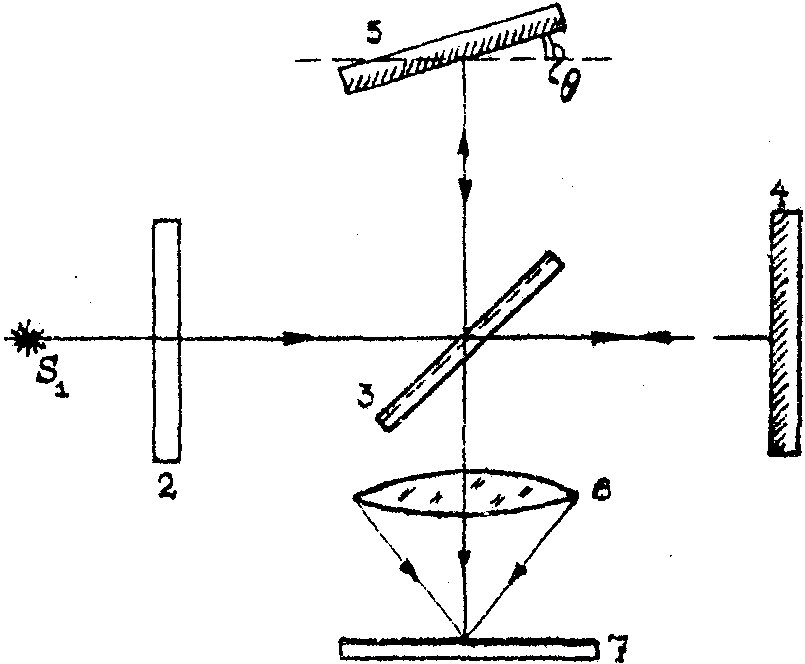
Рис.1. Схема интерферометра Майкельсона для записи Фурье-голограммы :
S1 – источник; 2 - диффузный рассеиватель; 3 - светоделитель; 4-5 - зеркала, 6 - линза; 7 - фотопластинка.
Вывод уравнения Фурье-голограммы делается следующим образом /9/ (см. обзор /10/) . Обозначим Е(x,у,z) электрический вектор плоской волны, наклоненный под углом 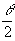 к оси интерферометра. Тогда поле в плоскости (x,у), перпендикулярной к оси Z, описывается следующим образом: к оси интерферометра. Тогда поле в плоскости (x,у), перпендикулярной к оси Z, описывается следующим образом:
- 200 -
Е( x,у) = E0exp[2p
iu
x×
Sin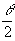 +w
t] (4) +w
t] (4)
где u
=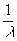 см-1 см-1, w
=2 p
сu
, с - скорость света. Вторая волна, идущая под углом 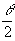 к оси, создает поле к оси, создает поле
Е( x,у) = E1exp[2p
iu
x×
Sin(-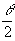 )+w
t+j
) (5) )+w
t+j
) (5)
где j
- разность фаз. Фотопластинка зарегистрирует интенсивность:
[I(x, у)]l
= 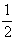 E2o+ E2o+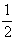 E21+ E1E0Cos[2p
u
x×
Sin E21+ E1E0Cos[2p
u
x×
Sin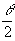 -j
] (6) -j
] (6)
Предположим, что интерферометр настроен таким образом, что j
=0, а также E2о=E21=I(u
), где I(u
) - интенсивность источника с волновым числом u
. Будем считать q
малым углом, тогда выражение (6) примет вид:
[I(x, у)]l
= I(u
)[1+Cos2p
u
q
x] (7)
В силу некогерентности между спектральными линиями источника голограмма, получаемая от источника со сложным спектром, будет выглядеть следующий образом:
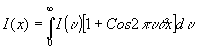 (8) (8)
При восстановлении голограммы излучается волна
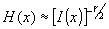 (9) (9)
где g
- коэффициент контрастности фотопластинки. При дискретном спектре и далеко отстоящих линиях I(u
) можно представить в виде
I(u
) = I1d
(u
-u
1)+I2d
(u
-u
2)+...+Ind
(u
-u
n) (10)
- 201 -
При подстановке (10) в (8) и (9) получим
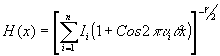 (11) (11)
Используя свойство голографической записи, интенсивность голограммы можно приближенно записать
I(x) @
1+e
(12)
тогда
Н( x} @
1-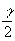 e
(13) e
(13)
а выражение (11) при g
<2 перепишется в виде
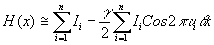 (14) (14)
Откуда следует, что переменные составляющие волны, исходящей от голограммы при восстановлении, пропорциональны интенсивностям отдельных линий спектра и коэффициенту контраста, голограммы g
. Пространственные частоты голограммы определятся выражением (2), а при малых q
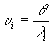 (15) (15)
При экспериментальной проверке метода использовалась ртутная лампа. На рис. 2 представлено восстановление спектральной Фурье-голограммы, выполненной в пучке гелий-неонового лазера. Было выделено пять линий ртути с разрешением 50 Å.
Метод голографической спектроскопии получил развитие в ряде последующих работ. Оригинальный метод безлинзовой голографической Фурье-спектроскопии предложен в работе /11/. Вначале изготавливается голограмма щели F1 и точечного источника S0, как показано на рис.3.
- 202 -
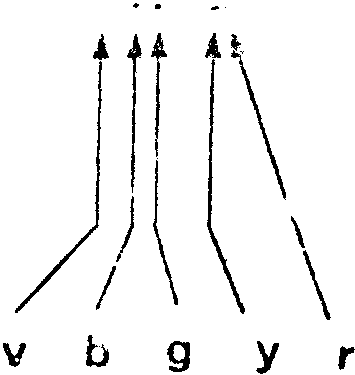
Рис. 2. Восстановленное изображение Фурье-голограммы ртутной лампы. Идентифицированные линия ртути:
v (3663 Å), b (4047 Å, 4078 Å), g (4358 Å),
y (5461 Å), r(5770 Å, 5790 Å)
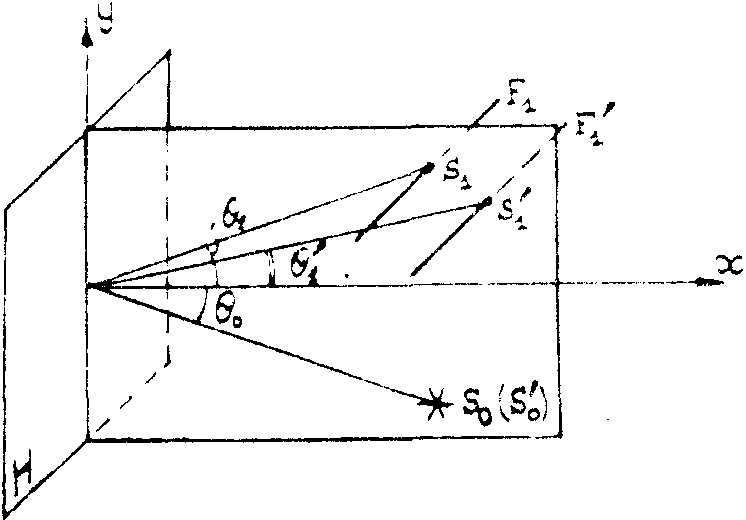
Рис.3. Схема записи голограммы Фурье.
F1 - щель; So - точечный источник; Н - голограмма; F1' - восстановленное изображение щели при замене источника So с длиной волны l
o на S1 с длиной волны l
1.
- 203 -
Для записи голограммы используется высококогерентный лазер. На втором этапе голограмма восстанавливается исследуемым источником So1. Голограмма будет восстанавливать ряд изображений щели F1', F1"... в соответствии со спектральным набором волн источника l
', l
"...
Авторы приводят выражение для дисперсии прибора:
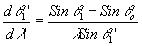 (16) (16)
Обозначения углов приведены на рис.3. Дисперсия растет с увеличением разности |
q
1- q
o|
. Удобно, что бы восстановленный спектр располагался вблизи оси X, для этого выбирается q
1=0. Дисперсия при этом будет
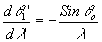 (17) (17)
Если при этом выбрать q
o = -45° и l
= 0.5 m
к, то 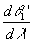 =1.4×
1O-4 рад/Å или около 0.5 мин/Å. =1.4×
1O-4 рад/Å или около 0.5 мин/Å.
Для экспериментального исследования метода была изготовлена голограмма площадью 25 мм. Источник So из соображений светосилы был заменен щелью. Полученная голограмма позволяла разрешать желтый дублет натрия (5890 и 5896 Å). Разрешающая способность прибора оценивается около – 1Å. Достоинство прибора - несомненная простота конструкции; недостаток - освещение голограммы расходящимся пучком, что приводит к ухудшении светосильности.
В работе /12/ используется метод голографической фурье-спектроскопии для исследования спектрального состава взрывающейся медной проволоки. При восстановлении голограммы были идентифицированы линии 4063, 4651, 5106 и 5782 Å.
При исследовании ртутной и кадмиевой ламп методом голографической Фурье-спектроскопии в работе /13/ было отмечено появление ложных линий в спектре. Объяснение этого явления дано в работе /14/. Автор интерпретирует это явление как появление "духов" с комбинированными пространственными частотами. Особенно это явление будет
- 204 -
проявляться, когда интенсивность спектра неравномерная, а фотоматериал для записи Фурье-голограммы выбирается с большим значением g
. Следствием этого является нелинейная запись голограммы. Нелинейная запись приводит к искажений синусоидальности записи пространственных частот голограммы и результатом служат высшие частоты при разложении голограммы. Второй причиной возникновения "духов" можно считать появление разностных частот и их комбинаций при восстановлении голограммы. Можно показать, что при линейной записи обратное Фурье-преобразование, которое происходят при восстановлении спектра, не дает ложных линий и только при нелинейной записи голограммы происходит необратимость преобразования и как следствие. возникновение "духов".
В работах /1,11-14/ рассматривалось применение голографической Фурье-спектроскопии к дискретным или линейчатым спектрам. Однако этот метод с успехом используется для исследования непрерывных спектров. В работе /15/ с помощью клиновидного Фурье-спектрометра исследовался спектр люминесценции родамина. В работе исследовалось влияние фотоматериала различной контрастности на характер восстановленного спектра. Результаты исследования представлены на рис.4. Анализируя кривые спектра при различных экспозициях, авторы приходят к выводу, что форма спектра малочувствительна к режиму получения голограмм, несмотря на большое различие в контрастности различных копий и отсутствие какого-либо контроля, обеспечивающего получение теоретически необходимого коэффициента контрастности g
=2. Практически слабая зависимость спектра первого порядка от условий получения голограммы спектра связана, по-видимому, с тем, что при сплошном спектре большая часть голограммы имеет малый контраст.
2. Разрешение спектральных линий с помощью голограмм Френеля
При исследований сложных спектров как дискретных, так и непрерывных, голографическая Фурье-спектроскопия позволяет получать неплохие результаты. Однако, для разрешения близких спектральных линий голографическая френелевская-спектроскопия имеет ряд преимуществ.
- 205 -
Рассмотрим принцип франелевской-спектроскопии с применением голографии /2/.
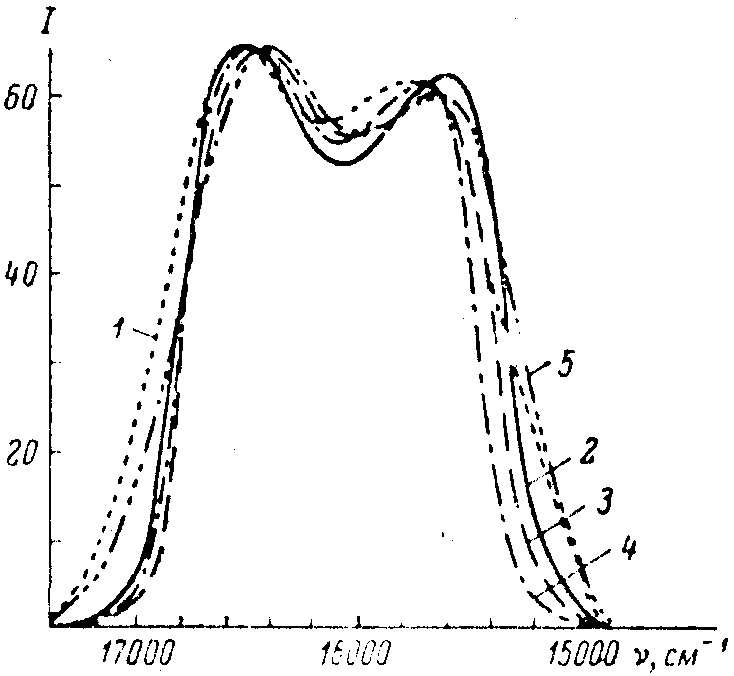
Рис.4. Спектры люминесценции родамина, измеренные на монохроматоре (1) и полученные методом голографической Фурье-спектроскопии с нормально экспонированной фотопленкой (2), недодержаной 13) и передержанной (4). 5 - спектр, полученный при обработке голограммы на ЭВМ.
Пусть источник имеет две близкие спектральные линии l
1 и l
2, тогда, если два коллимированных пучка сходятся на голограмме под углом q
, голограмма Френеля будет содержать два синусоидальных распределения с пространственными частотами
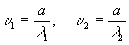 , ,
где a = 2Sin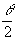 (18) (18)
При этом естественно предполагается, что излучение с длиной волны l
1 не интерферирует на голограмме с излучением с длиной волны l
2, а объемы когерентности излучений достаточны для записи голограммы.
Покажем, что по восстановленному изображению голограммы можно
- 206 -
определить расстояние между спектральными линиями D
l
=l
2-l
1. Для этого поместим голограмму в коллимированный пучок лазера с длиной волны l
о (рис.5). Лазерный свет будет дифрагировать на голограмме, создавая два пучка I1 и I2 -направленных под углами y
1 и y
2 в соответствии с пространственными частотами u
1 и u
2. Если D
l
<<l
1 и l
2, то в результате интерференции пучков I1 и I2 получим в плоскости X' широкие интерференционные полосы c частотой:
u
o = 2Sin(D
y
/2)/l
o »
D
y
/l
o (19)
т.к. величина D
y
=y
1-y
2 мала. Углы y
1 и y
2, определим из условия Брегга:
Siny
1 = l
ou
1, Siny
2 = l
ou
2 (20)
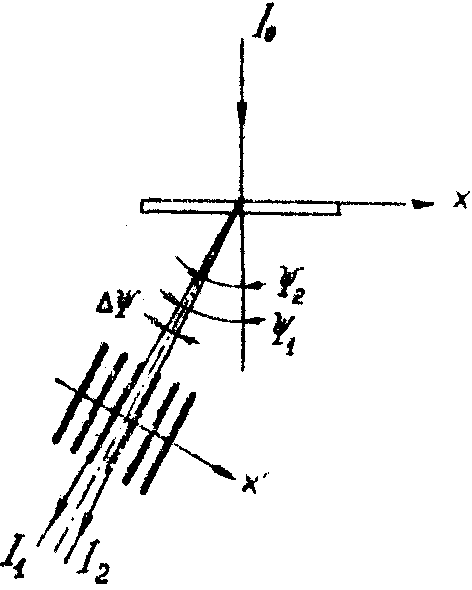
Рис. 5. Образование линий биений при восстановлении голограммы Френеля.
- 207 –
Подставим значения y
1 и y
2 из (19) в (20), получим
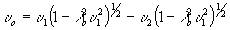 (21) (21)
При замене u
1 и u
2 через l
1 и l
2= l
1+ D
l
получим
 (22) (22)
Оставив члены первого порядка относительно D
l
, из выражения (22) найдем
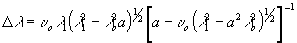 (23) (23)
Таким образом, голограмма Френеля позволяет определять расстояние между линиями дублета, в силу того, что при восстановлении голограммы Френеля возникают биения с частотой u
о, отвечающие двум линиям источника (l
1 и l
2), несмотря на полное отсутствие взаимной когерентности между ними.
Для экспериментальной проверки предлагаемого метода использованы три линии ртутной лампы: зеленая (l
3 = 5460,7 Å) è две близкие оранжевые (l
о1 = 5769,6 Å, l
о2 = 5790,6 Å). Голограмма Френеля была получена с помощью оптической, схемы, представленной на рис.6. Отличительной особенностью оптической схемы можно считать использование специального призменного двухлучевого интерферометра (9) /16/, который позволяет выравнивать разность хода для осевых пучков и производить совмещение соответствующих точек для всего поля. Настройка оптической системы производится микроскопом (11), с помощью которого выбирается зона максимального контраста интерференционных полос в плоскости голограммы /17/. Эффективные размеры голограммы для зеленой и оранжевой линий D равны D3 = 18,3 мм и D0 = 13,2 мм. Средняя частота интерференционных линий u
3 = 291 I/ мм, u
o = 275 I/ мм.
На рис.7а,б приведены изображения, восстановленные из голограмм
- 208 -
в коллимированном пучке гелий-неонового лазера. На рис.7в дана микроденситограмма восстановленного изображения.
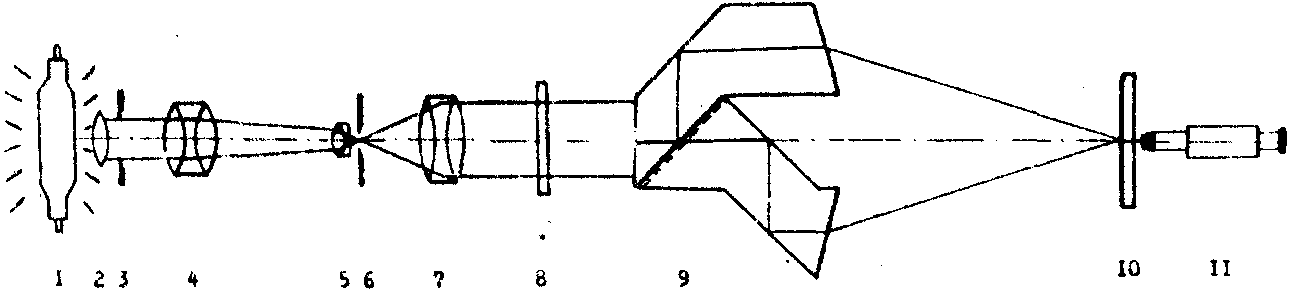
Рис.6. Оптическая схема установки, использованная для получения голограмм в квазикогерентном свете.
1 - ртутная лампа; 2,4,7 - коллимирующие объективы: 3 - полевая диафрагма; 5 - микроскопный объектив 20х; 6 - диафрагма Æ
0.3 мм; 8 - светофильтр, обрезающий коротковолновую компоненту, 9 - призменный двухлучевой интерферометр /3/; 10 - фотопластинка; 11 - микроскоп.
По биениям, соответствующим оранжевому дублету (низкочастотная огибающая рис.7в), найдена частота u
o, по которой рассчитывалось расстояние между линиями дублета. Найденный результат (20,1±
1,6) Å ñогласуется с данными, полученными другими методами. Высокочастотная модуляция (рис,7в) позволяет определить расстояние между зеленой и оранжевой линией (330±
10) Å.
Подъем денситометрической кривой в левой части рис.7в определяется расхождением пучков, дифрагированных на решетках, записанных на голограмме от зеленой и оранжевых линий источника. При увеличении расстояния от голограммы до плоскости восстановления пучки разделяются, кривая, отвечающая биениям оранжевого дублета, симметрируется, а высокочастотная модуляция, соответствующая биениям l
3 и l
o, исчезает.
Размер голограммы D позволяет определить эффективную длину
- 209 -
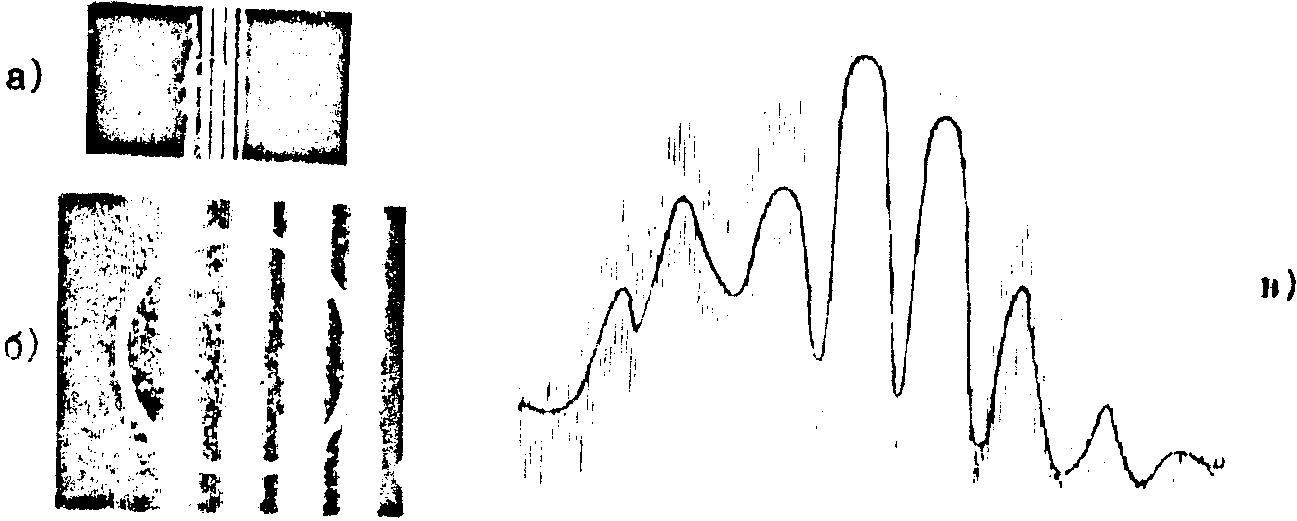
Рис. 7. а) восстановленное изображение голограммы;
б) микроструктура восстановленного изображения голограммы (8х ) в указанном кружком месте,
в) микроденситограмма восстановленного изображения.
Низкочастотная огибающая фотометрировалась с широкой щелью и соответствует биению оранжевого дублета. Высокочастотная составляющая ( ) отвечает биению зеленой и оранжевой линий ртутной лампы.
когерентности источника.
L = Dtg(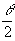 ) (24) ) (24)
где q
- угол схождения пучков на голограмму. Откуда длины когерентности для зеленой и оранжевой линий получаются: L3 = 1,45 мм, L0 = 1,04 мм. Длина когерентности связана с шириной линии источника D
l
как L=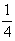 l
2/D
l
/18/, откуда D
l
3 l
2/D
l
/18/, откуда D
l
3 = 0,5 Å, D
l
o = 0.8 Å. Резюмируя изложенное, отметим, что
1) увеличение точности в голографической спектроскопии Френеля объясняется тем, что отдельные линии источника коррелированны при восстановлении голограммы, т.к. между исследуемыми линиями возникают биения, а в Фурье-спектроскопии отдельные линии разделяются;
- 210 -
2) в Фурье-спектроскопии разрешение связано с аберрациями Фурье-преобразующей оптической системы, что особенно важно при разделении близких линий;
3} голограмма Френеля позволяет легко определять такие параметры источника как эффективную длину когерентности источника и ширину спектральных линий;
4) голограмма Френеля позволяет производить интерференционное сравнение различных линий источника, либо независимые источники излучения.
Все голограммы были записаны на пластинках ВРЛ.
3. Разрешающая способность в голографической спектроскопии
Произведем оценку разрешающей способности в голографической спектроскопии. Строук предлагает оценивать разрешение следующим образом. Пусть голограмма Фурье записана при длине волны источника l
, с объективом, имеющим фокальную длину ¦
, а восстановление производится в лазерном свете с длиной волны l
L. При этих условиях голограмма произведет отклонение центрального луча на угол q
, определяемый формулой Брегга Sinq
=l
L/aL, а координата изображения в плоскости восстановления
x
= ¦
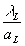 = ¦
l
Lu
L (25) = ¦
l
Lu
L (25)
где u
L - частота решетки, создаваемой интерференционными полосами на голограмме, обратно пропорциональна длине волны излучения при записи и u
L = c/ l
(где С - постоянная), тогда
D
x
= ¦
l
Lu
L = -c¦
l
L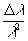 (26) (26)
С другой стороны, спектральный предел разрешения, согласно критерию Релея, можно записать в виде.
D
x
= ¦
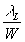 (27) (27)
где W - ширина голограммы.
Приравнивая правые части выражений (26) и (27) получим
- 211 -
разрешающую способность спектроскопической голограммы:
R.P. = 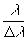 = Wu
L = N (28} = Wu
L = N (28}
где N - общее число интерференции иных линий записанных на голограмме. Таким образом, мы пришли к выражению, что, как и для обычной дифракционной решетки, разрешающая способность голограммы определяется полным числом интерференционных линий.
Приведем примеры разрешающей способности для конкретных экспериментов. В работе Stroke /1/ при исследовании спектра ртутной лампы получено разрешение 50 Å (îранжевый дублет 21 Å íе разрешается) в то же время, согласно выражению (28) разрешающая способность равна 9Å (ширина голограммы W = 20 мм, частота u
L = 30 мм-1}. В работе /2/ на аналогичном спектре получено разрешение 1,6Å при теоретическом 1.04Å (W = 18.3 мм, u
L = 291 мм-1, l
= 5460Å).
Увеличение разрешающей способности голограммы в работе /2/ получено за счет того, что удалось записать большее число линий. Уменьшение разницы в разрешающей способности теоретической и экспериментальной определяется тем, что при записи Фурье-голограмм экспериментатору приходится записывать большие перепады интенсивности, которые трудно уложить в линейный участок кривой почернения фотоматериала, в то время как при записи голограмм Френеля записывается синусоидальная кривая с главной модуляцией.
Литература
G.W.Stroke, A.Funkhouser. Phys. Letters, 16, 272 (1965).
B.G.Turukhano, N.Turukhano. Opt. Commun., 6, 177 (1972).
3. P.Fellgett. Thesis (Cambridge University), 1951.
4. P.Jacquinot. JOSA, 44, 761 (1958).
5. J.Strong. JOSA, 47, 354 (1957).
6. J.Connes. Rev.Opt., 40, 45 (1961); P.Connea.Rev.Opt., 35, 37 (1958).
7. П.Ф.Паршин. Материалы 1 шк. по голографии, Л., стр.134, 1971.
8. G.W.Stroke. An Introduction to Coherent Optics and Holography, N.Y., 1966.
9. G.W.Stroke. Physics Deel, 33, 255 (1967).
- 212 -
10. П.Ф.Паршин, А.А.Чумаченко, УФН, 103, 553 (1971).
11. B.Lefevre, C.Durou. C.r. Acad.Sci., 269 (9), В359 (1969).
12. T.Isuno, R.Takahashi. Time-resolved spectroscopy using holographic recording, 9 Int. congress on high-speed photography, Denver, Colorado, 1970.
13. K.Iosbihara, A.Kitade. Japan. J.Appl.Phys., 6, 116 (1967).
14. W.T.Plummer. Japan. J.Appl.Phys., 6, 1250 (1967).
15. Г.И.Косоуров. И.П.Петров. Опт. и спектр. 27, 337 (1969).
16. Б.Г.Турухано, Н.Турухано. Опт. и спектр. 25, 309 (1968).
17. Б.Г.Турухано, Н.Турухано. ЖТФ, 38, 757 (1968).
18. Ю.Н.Денисюк. ДАН СССР, 144, 1275 (1962).
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

