|
|
 |
 |

|
| |
ИССЛЕДОВАНИЕ ВОЗМОЖНОСТЕЙ ИЗУЧЕНИЯ РАСПРЕДЕЛЕНИЯ
ЛИНЕЙНЫХ ЭЛЕМЕНТОВ ИЗОБРАЖЕНИЯ С ПОМОЩЬЮ ОПТИЧЕСКОГО ФИЛЬТРА
В.А.Лихтерман, И.А.Черкасов
В статье исследуются особенности образования двумерных спектров от различных, статистически распределенных, линейных элементов изображения. Полученные выводы показывают, что изучение особенностей распределения линейных элементов при дешифрировании аэроснимков, геофизических и фотографических исследованиях не может быть достоверным при выполнении анализа только двумерных спектров. Этот анализ необходимо дополнять оптической фильтрацией изображения.
В конце 60-х годов за рубежом, а затем и у нас, в СССР, были поставлены первые опыты по автоматизации процесса дешифрирования аэроснимков и обработке карт линейных элементов, основанные на методе оптической фильтрации изображения с применением оптических квантовых генераторов (ОКГ).
За рубежом результаты этих опытов были опубликованы в ряде работ, посвященных, главным образом, описанию применения метода оптической фильтрации изображения в различных областях знания. К этим работам относятся публикация Пинкуса /1/ о применении указанного метода обработки информации в геологических исследованиях, публикации Фонтанеля и др. /2,3/ о решении ряда задач с помощью оптической фильтрации изображения в гидрологических, археологических. гляциологических и геологических изысканиях, публикация Шевалье и др. /4/ об аналогичных исследованиях в области гидрологии, археологии и городском строительстве и ряд других публикаций.
- 177 -
Основная заслуга приведенных работ состоит в том, что они способствовали популяризации и расширению границ применения метода оптической фильтрации изображения. Однако, вместе с тем для многих из них характерно наличие методических погрешностей и ошибочных рекомендаций, объясняемых механическим распространением анализа закономерностей образования дифракционных картин (двумерных спектров) от идеальных решеток на дифракционные картины от линейных элементов природных объектов, изображающихся на аэроснимках.
Как известно /5/ , распределение амплитуд света, дифрагированного идеальной решеткой, в ее двумерном спектре может быть охарактеризовано общей формулой:
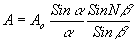 (1) (1)
где А 0 - амплитуда света, создаваемая одной щелью решетки по первоначальному направлению; 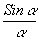 - ход распределения света, дифрагированного одной щелью решетки; Sinb
N - распределение света, дифрагированного решеткой, состоящей из N щелей. Величины a
и b
, входящие в формулу (1), зависят от длины волны l
используемого источника света, ширины b и периода d щелей исследуемой решетки и угла j
дифракции лучей света на решетке. - ход распределения света, дифрагированного одной щелью решетки; Sinb
N - распределение света, дифрагированного решеткой, состоящей из N щелей. Величины a
и b
, входящие в формулу (1), зависят от длины волны l
используемого источника света, ширины b и периода d щелей исследуемой решетки и угла j
дифракции лучей света на решетке.
Анализ формулы (1) на экстремальные значения позволяет получить также хорошо известную и применяемую в спектральном анализе зависимость между определяемой длиной волны l
исследуемого источника света, известным значением периода d дифракционной решетки и измеренной величиной К между максимумами света в спектре этой решетки:
d×
K = Fl
(2)
где F - фокусное, расстояние преобразующей линзы, с помощью которой строится двумерный спектр решетки.
При дешифрировании аэроснимков эта зависимость (2), в отличие от спектроскопии, используется для нахождения среднего значения периода d линейных элементов природного объекта по известному
- 178 -
значению длины волны l
, применяемого источника света, т.е. решается как бы обратная задача.
Изображения природных объектов на аэроснимках, даже обладающих заметной периодичностью, таких, например, как морские волны, отличаются от идеальных дифракционных решеток, поэтому объяснение закономерностей построения двумерных спектров преобразования Фурье от этих объектов в соответствии с зависимостями (1) и (2) требует дополнительного обоснования.
Такое обоснование для объяснения особенностей образования двумерных спектров от природных объектов, обладающих заметной периодичностью, было выполнено Ю.Д.Шариковым /6/, который распространил на эти объекты теорию несовершенных дифракционных решеток, разработанную Спарроу /7/.
Однако объекты с заметной периодичностью своих элементов встречаются в природе крайне редко. Большей частью периодические элементы природных объектов такие, как геологические и гляциологические трещины, гидрографическая сеть, различного рода изолиний, сейсмограммы и т.п., широкое изучение которых с помощью дифракционного метода наметилось в последние годы, не могут рассматриваться в качестве несовершенных дифракционных решеток, т.к. частота их распределения изменяется в широких пределах. В то же время выяснение закономерностей распределения этих объектов путем анализа их двумерных спектров, оптической фильтрации их изображения и фотоэлектронной регистрации количества света, пропускаемого ими, до сих пор производится на основании формулы (1), характеризующей распределение амплитуд света в двумерном спектре идеальной решетки.
Очевидно, что правомочность распространения особенностей такого частного случая на всевозможные виды изменения частот других линейных элементов может быть установлена только после проведения исследований, аналогичных тем, которые выполнил Спарроу для несовершенных дифракционных решеток.
Рассмотрим особенности образования двумерных спектров решеток, частота ,штрихов которых подчинена нормальному закону распределения, как наиболее близко отвечающего существующим закономерностям распределения элементов природных объектов.
- 179 -
Остановимся на двух случаях, когда в рамках одного и того же нормального закона распределения изменение частоты штрихов решетки происходит постепенно и когда это изменение частоты отвечает любой случайной последовательности. В обоих случаях ширину b всех щелей решеток будем считать величиной постоянной, а наименьший период d1 примем равным 2b.
В соответствии с теорией математической статистики /8/ построим решетку с нормальным законом распределения частот щелей, значения величин и нормированного количества периодов которой представлены в таблице 1.
Таблица 1
|
Величины периодов решетки di в долях наименьшего периода |
1.0 |
1.4 |
1.8 |
2.2 |
2.6 |
3.0 |
3,4 |
3.8 |
4.2 |
4.6 |
5.0 |
|
Нормированное количество периодов pi |
1 |
2 |
4 |
5 |
7 |
8 |
7 |
5 |
4 |
2 |
1 |
Для облегчения последующих выводов предположим, что мы имеем две нормально распределенные решетки типа, заданного таблицей 1, общей начальной щелью, но направленные от этой щели в разные стороны. Очевидно, что такое удвоение решетки не искажает нормального закона распределения ее частот, но в то же время упрощает задачу отыскания результирующего возмущения, дифрагированного всей решеткой света, т.к. позволяет представить его в виде линейной комбинации возмущений от ряда отдельных идеальных решеток, расположенных симметрично относительно общего центра - начала координат.
Выберем систему плоских прямоугольных координат так, чтобы ось абсцисс лежала в плоскости решетки и была направлена перпендикулярно к ее щелям, а ось ординат совпадала с направлением, противоположным направлений падающего на решетку параллельного пучка
-180 -
лучей света. За начало координат примем центр щели, соответствующей наименьшему периоду d (рис.1).
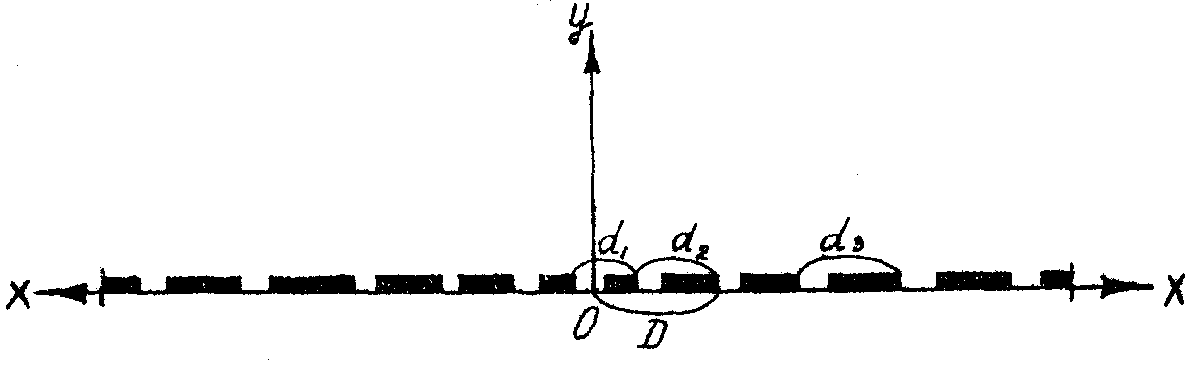
Рис.1. Иллюстрация выбора начала и направления осей координат при исследовании светового возмущения на нормально распределенной решетке.
Для отыскания светового возмущения оказываемого той или иной решеткой с периодом di и количеством щелей pi в направлении, определяемом углом дифракции j
с первоначальным направлением, необходимо найти сначала действия, оказываемые каждой щелью, и просуммировать их с учетом разности фаз волн света, зависящих от положения этих щелей на плоскости экрана.
Как известно /1/ , действие какой-либо щели в направлении может быть представлено в форме
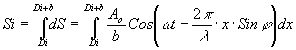 (3) (3)
где ао - амплитуда волны света, посылаемого щелью с шириной b в первоначальном направлении; Di - расстояние от начала координат до края щели; dx - ширина элементарного участка щели.
Используя эту зависимость (3) и учитывая из рис.1 значения расстояний Di, найдем результирующее возмущение от центральной решетки с периодом, равным d1, и количеством щелей p1=3:
- 181 -
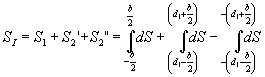 (4) (4)
Проинтегрировав выражение ( 3) и подставив значения пределов интегрирования из (4), после выполнения известных /9/ тригонометрических преобразований получим:
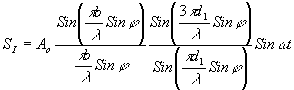 (5) (5)
Найдем возмущение, создаваемое второй решеткой с периодом d2=1.4d1 и состоящей из 4-х щелей, попарно расположенных симметрично относительно начала координат:
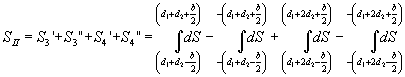 (6) (6)
Выполнив необходимые действия и произведя преобразования, получим:
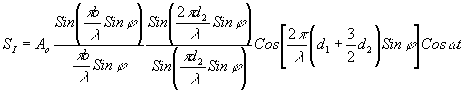 (7) (7)
Введя обозначение
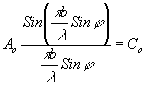
- 182 -
и применяя этот путь расчета возмущений от рассмотренных симметричных решеток к остальным решеткам, получим общую формулу :
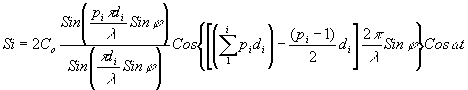 (9) (9)
где pi и di - количество и величина периодов штрихов решеток, заданные в таблице 1.
Анализ формулы (9) показывает, что световые возмущения от разных пар симметричных решеток приходят к плоскости преобразования Фурье в одной и той же фазе, но имеют разные значения амплитуд. Отсутствие сдвига по фазе позволяет поэтому определить амплитуду общего возмущения, создаваемого всей решеткой, как алгебраическую сумму амплитуд отдельных возмущений (9), т.е.
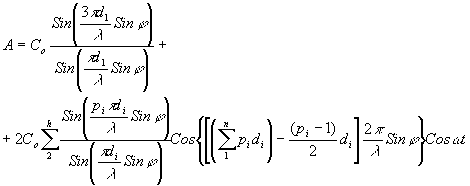 (9) (9)
На рис.2 представлены нормально распределенная решетка, построенная по данным таблицы 1, ее двумерный спектр и график распределения интенсивности света по главным максимумам этого спектре. Пунктирной линией на графике показан примерный ход распределения интенсивности света по главным максимумам двумерного спектра идеальной решетки с периодом штрихов, равным 3d, т.е. с таким значением величины периода, которая отвечает среднему значению периода нормально распределенной решетки.
Как следует из графика и изображения двумерного спектра на рис.2, при нормальном законе распределения штрихов решетки происходит перераспределение интенсивности света по максимумам спектра и изменяется само положение этих максимумов. Так, если для двумерного спектра идеальной решетки характерно постепенное уменьшение интенсивности света по мере возрастания порядковых номеров максимумов, то в соответствующем спектре нормально распределенной
- 183 -
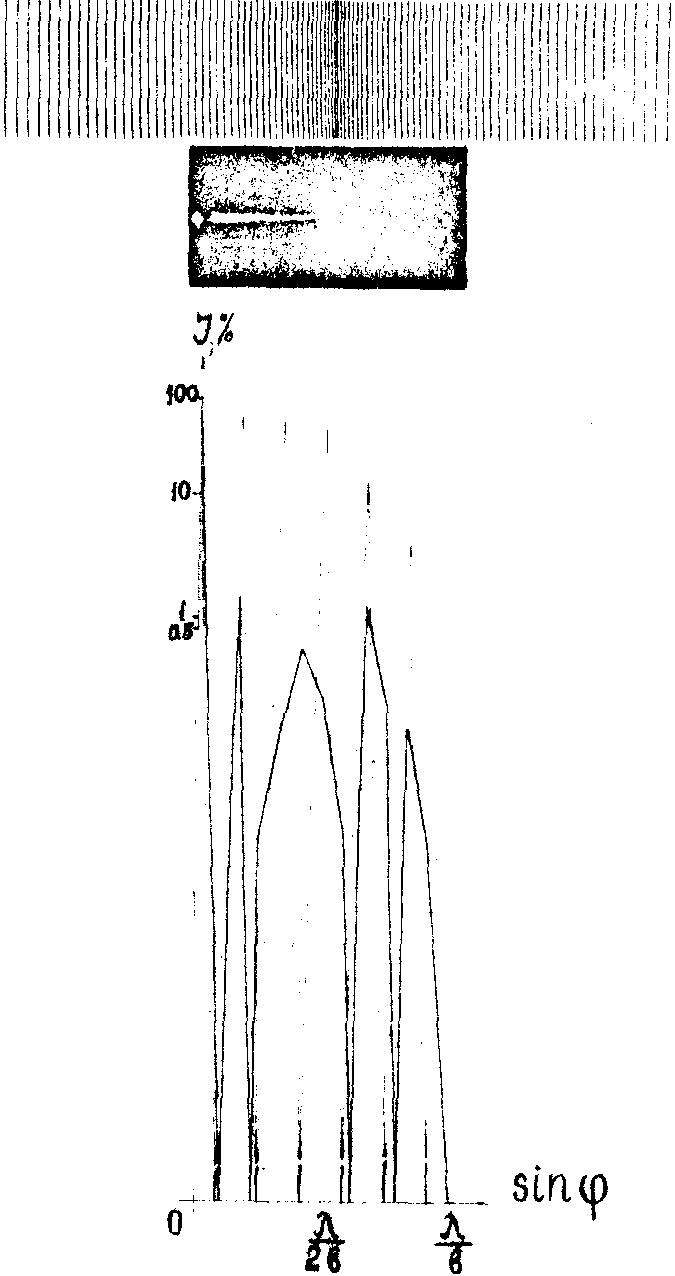
Рис.2. Нормально распределенная решетка с постоянным изменением частот штрихов, ее двумерный спектр и график распределения интенсивности света в спектре.
решетки интенсивность максимума света третьего порядка оказывается Дольше интенсивности максимума света второго порядка. Кроме того, положение максимума света в двумерном спектре равномерно распределенной решетки приходится на минимум света между максимумами второго и третьего порядков двумерного спектра идеальной решетах, т.е. при нормальном законе распределения штрихов решетки нарушается
- 184 -
правильность чередования максимумов света в двумерном спектре ее.
Последнее полученное обстоятельство поставило под сомнение возможность выполнения анализа двумерного спектра объекта, с целью определения средних величин частот его элементов, и поэтому потребовало более тщательного обоснования его. Дело в том, что график на рис.2 был построен по 12 точкам, для которых по формуле (10) были рассчитаны значения величины интенсивности света, т.е. точность построения графика могла не обеспечить правильности полученных по нему выводов. Для исключения ошибок построения были выполнены по формуле (10) трудоемкие расчеты значения величины интенсивности для 104 точек. Результаты этих вычислений нанесены на график, представленный на рис.3. На этом же графике пунктирной линией показано распределение интенсивности света в двумерной спектре идеальной решетки и сплошной жирной линией - в двумерном спектра нормально распределенной решетки, соответствующей значениям, приведенным на графике рис.2.
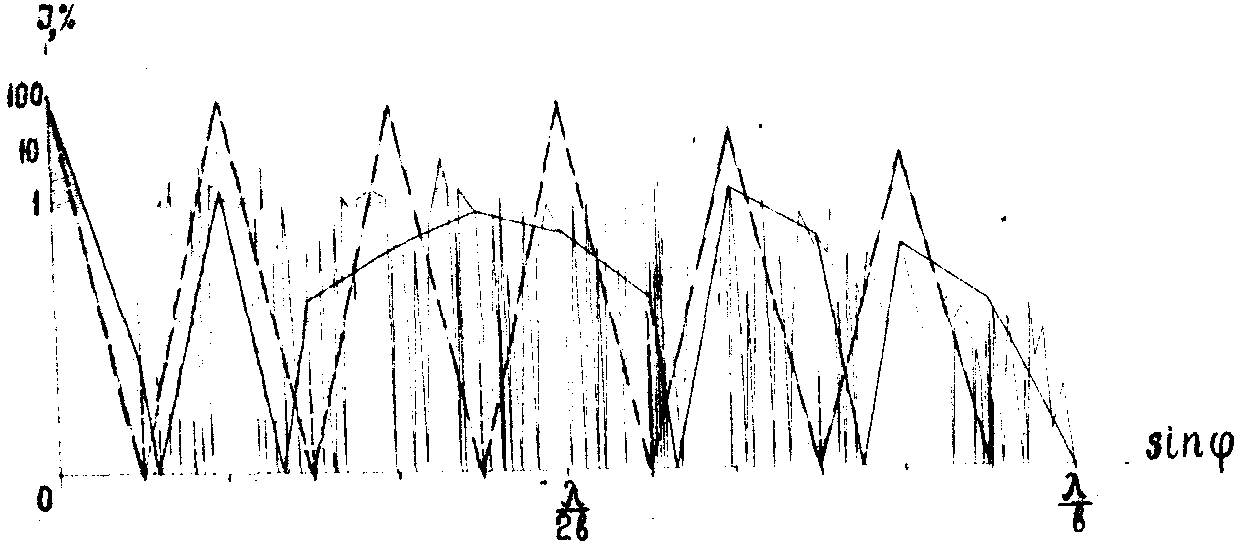
Рис.3. Уточненный график распределения интенсивности света в спектре от решетки, показанной на рис.2.
- 185 -
Сравнение графиков показывает, что хотя дополнительные вычисления и приводят к расчленению целых изображений прежних максимумов на сгруппированные совокупности изображений новых максимумов, общий ход распределения интенсивностей света по двумерному спектру нормально распределенной решетки остается тем же. Таким образом, полученные ранее выводы о изменении порядка чередования максимумов света в зависимости от закона распределения штрихов решетки получили дополнительное подтверждение.
Построенная нами решетка с нормально распределенными штрихами на рис.2 состоит из нескольких отдельных решеток, расположенных рядом друг с другом в правильном порядке по мере изменения величины их периодов. Однако, подчинение природного объекта закону нормального распределения вовсе не предполагает правильности последовательного чередования его элементов, поэтому необходимо выяснить, как изменение этой последовательности отражается на распределении интенсивности в двумерном спектре.
Для проверки этого положения из решеток с различными значениями величин периодов, заданных в таблице 1, был составлен произвольный ряд, представленный в таблице 2.
Таблица 2
|
Величины периодов решетки di |
1.0 |
3.8 |
2.6 |
3.0 |
4.6 |
3.4 |
5.0 |
5.2 |
4.2 |
1.4 |
1.8 |
|
Количество периодов pi |
1 |
5 |
7 |
8 |
2 |
7 |
1 |
5 |
4 |
2 |
4 |
Решетка, полученная в результате перестановки составляющих решеток, так же, как и ранее рассмотренная, подчинена нормальному закону распределения, т.к. выполненные перестановки не изменили нормированных значений чисел периодов ее штрихов.
На рис.4 показан вид этой решетки, ее двумерный спектр и график распределения интенсивностей по главным максимумам этого спектра, рассчитанный по формуле (1.46). Пунктирной кривой, как
- 186 -
и ранее, показан ход распределения интенсивности света по главным максимумам соответствующей идеальной решетки.
Анализ графика на рис.4 показывает, что как и в предыдущем случав на рис. 2 распределение интенсивности света по главным максимумам не соответствует правильному убыванию ее по мере возрастания порядкового номера максимума. Кроме того, как и ранее, наблюдается нарушение правильности чередования положения максимумов в двумерном спектре этой решетки.
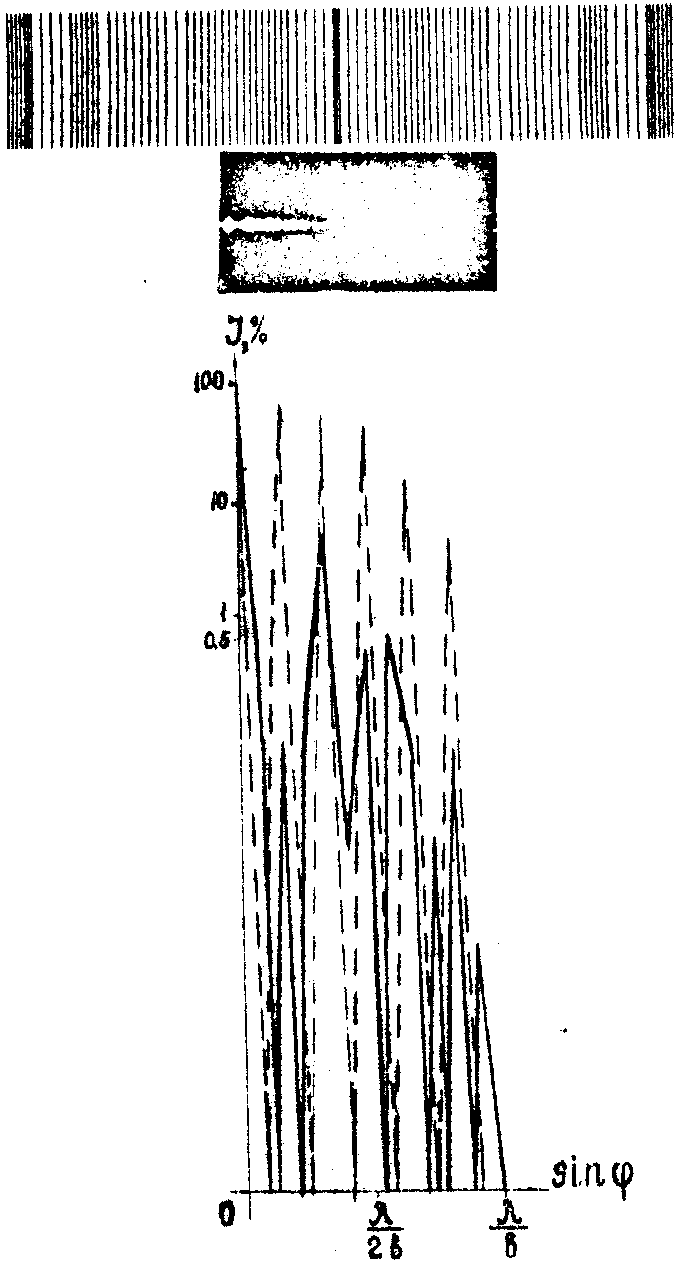
Рис.4. Нормально распределенная решетка со случайным изменением частот штрихов, ее двумерный спектр и график распределения интенсивности света в спектре.
- 187-
Сравнение графиков на рис.2 и 4 между собой позволяет сделать вывод о том, что распределение интенсивности света в двумерном спектре решетки зависит как от закона распределения ее штрихов, так и от различной последовательности штрихов и их числа в пределах одного закона. Это, в свою очередь, дает основание предположить, что нельзя только по двумерным спектрам природных объектов установить достоверно особенности распределения элементов этих объектов, т.к. любые изменения вида изображения, будь то различие в числе элементов его и различие в порядке их чередования, получают свое отражение в двумерном спектре. Поэтому при дешифрировании аэроснимков двумерные спектры целесообразно использовать для распознавания объекта по характеру и интенсивности изображения его спектра, путем его анализа и сравнения с полученным ранее эталонным материалом /10,11/. Для определения же закономерностей распределения элементов внутри каждого типа объектов необходимо выполнять и оптическую фильтрацию их изображения. Полученные выводы дают возможность рекомендовать проводить фотоэлектронную регистрацию не в плоскости Фурье, как рекомендуют некоторые авторы, а в плоскости изображения. Эти выводы целесообразно учесть при использовании метода в геофизических и фотографических исследованиях, где анализу двумерного спектра отводится основная роль.
Кроме этого, следует отметить, что природные объекты, изображающиеся на аэроснимках, как правило, относятся к классу двумерных решеток, поэтому при анализе дифракционных картин или при выполнении фильтрации изображения необходимо учитывать и особенности дифракции света на этих решетках.
- 188 -
Литература
1. H.J.Pincus. Geological applications of optical data processing. J.Geophysical Research, 71, 20, 4861, 1966.
2. A.Fontanel, G.Grau, J.Laurent et Montadert. Methode détude et depoulement des photographies aeriennes par difraction de la lumiere coherence issue dún laser. Societe Francaise de Photogrammetrie, Bulletin, 2, 111, 14, 1967.
3. A.Fontanel, Le filtrage optique en lumiere coherente. Kodak-Pathe Photogr. Aerienne, 23, 34, 1969.
4. R.Chevallier, A.Fontanel, G.Grau, M.Guy. Application du filtrage optique a l'euude des photographies aeriennes. Soc. Francaise de Photogrammetrie, YII.I, 1968.
5. Г.С.Ландсберг. Оптика. Гос.техн.теор.изд., М., стр.141-163, 1954.
6. Ю.Д.Шариков. Обработка одиночных аэроснимков дифракционный методом. В кн. Применение аэрометодов для исследования моря, гл.Y, стр.156-178. Изд. АН СССР, М.-Л., 1965.
7. С.М.Sparrow. Theory of imperfect gratings. The Astrophysical Journal, ХLIХ, 2, 65, march, 1919.
8. Н.В.Смирнов, И.В.Дунин-Барковский. Курс теории вероятностей и математической статистики. Изд. "Наука", Ь., стр.133-157, 1969.
9. В.И.Смирнов. Курс высшей математики” Гос.техн.теор.изд., М., 1, стр.407-409, 1954.
10. Г.Г.Лендарис, Г.Л.Стенли. Метод дискретизации дифракционных картин для автоматического распознавания образов. ТИИЭР, № 2, стр.22-40, 1970.
11. В.А.Лихтерман. Применение оптического фильтра с когерентным источником света для дешифрирования аэроснимков и обработки карт линейных элементов. Тезисы доклада на научно-технической конференции "Использование ОКГ в современной технике". Л., стр.27, 1971.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

