|
|
 |
 |

|
| |
МУЛЬТИПЛИКАЦИЯ ИЗОБРАЖЕНИЙ И ИХ ПРОСТРАНСТВЕННЫХ
ЧАСТОТНЫХ СПЕКТРОВ
Л.П.Карпов, А.С.Блок
В ряде задач, таких как построение оптико-электронных систем распознавания, производство интегральных схем и других, требуется получение определенного числа неискаженных изображений при подаче на вход мультиплицирующего устройства одного изображения.
В настоящей работе кратко рассматриваются методы: голографические, методы дифракционных решеток и метод оптического туннеля. Дается их математическое описание.
Введение
Сущность задачи мультипликации состоит в одновременном формировании группы непересекающихся, идентичных изображений или пространственных частотных спектров некоторого объекта.
В настоящее время развитие методов мультипликации стимулируется как необходимостью совершенствования технологии производства интегральных схем, так и проблемой создания многоканальных систем обработки информации с параллельным анализом. Основной при использовании методов мультипликации в микроэлектронике является проблема получения изображений с высоким качеством. Такие мультипликаторы должны обеспечивать высокую разрешающую способность и малые искажения изображений. При создании многоканальных систем обработки во многих случаях требования к качеству мультиплицированных изображений и их пространственных спектров по сравнению с требованиями в микроэлектронике могут быть значительно снижены, однако в этом случае мультипликатор не должен вносить больших потерь света, т.е. должен обладать высокой эффективностью.
- 137 -
Выбор конкретного метода мультипликации в системах обработки определяется решаемой задачей, а также видом используемых носителей информации (фотопленка, электронно-лучевая трубка и т.д.) и типом источника излучения (когерентный, некогерентный).
В настоящее время известен ряд методов мультипликации изображений и их пространственных спектров.
а) Матрица точечных отверстий /1/. Этот метод характеризуется низкой разрешающей способностью и большими потерями света.
б) Метод, использующий матрицу линз малого диаметра. Он дает лучшие результаты, чем /1/ , однако качество изображений также невысокое, поскольку простые линзы страдают от аберраций и искажений. Кроме этого, такой мультипликатор работает с сильным уменьшением изображения (мал размер поля мультиплицированных изображений), что не всегда удобно для построения многоканальных систем обработки.
в) Методы, основанные на явлении двойного лучепреломления /2,3/. Авторы не приводят данных, характеризующих качество получаемых в этих случаях изображений. Очевидно, что при необходимости получения большого числа изображений мультипликатора, основанные на этих методах, будут громоздкими, дорогостоящими, сложными в юстировке, а потери света будут велики.
г) Метод оптического туннеля и метод, использующий мозаику зеркал /4/. Оба метода основаны на отражении света от плоских зеркальных поверхностей. Если метод /4/ едва ли найдет широкое применение из-за сложности юстировки, низкого качества мультиплицированных изображений, а также того обстоятельства, что мультиплицированные изображения группируются не в одной плоскости, то метод, использующий оптический туннель, позволяет реализовать сравнительно простой и качественный мультипликатор изображений и их пространственных спектров, работающий как в когерентном, так и в некогерентном свете.
Недостатком мультипликатора на оптическом туннеле является неодинаковая яркость мультиплицированных изображений. Однако, сравнительно высокая эффективность туннельного мультипликатора позволяет использовать выравнивающую маску, если такая необходима,
д) Методы, использующие голограммы Фурье и Френеля, и сложные дифракционные решетки /5,6,7,8/. Эти методы представляются
- 138 -
перспективными при создании многоканальных устройств обработки информации. Преимущества этих методов состоят в одинаковой яркости мультиплицированных изображений, в возможности увеличения контраста за счет исключения постоянной составляющей в простоте реализации, причем метод /8/ не требует линз для мультипликации и дает возможность одновременно получать как мультиплицированные изображения, так и их пространственные спектры. Последнее обстоятельство обеспечивает возможность одновременного использования для обработки самих изображений и их пространственные спектры, что может оказаться важным преимуществом, в частности, при создании оптико-электронных распознающих систем. Недостатком этих методов является низкая дифракционная эффективность, а также наличие шумов, вносимых эмульсией. Наиболее перспективны, по-видимому, фазовые голограммы и дифракционные решетки,
е) Методы, использующие простые амплитудные и фазовые решетки /9,10/.
Из них в системах обработки предпочтительнее применение метода /10/ в сочетании с каскадным способом построения мультипликатора. В тех случаях, когда не требуется большого числа мультиплицированных изображений, количество каскадов будет небольшим, а мультипликатор - несложным. Фазовые решетки обладают сравнительно высокой эффективностью, и, как будет показано, при соблюдении определенных условий яркость мультиплицированных изображений может быть сделана одинаковой.
В дальнейшем рассмотрим подробнее те методы, которые, по мнению авторов, наиболее перспективны при создании многоканальных систем обработки и, в частности, для построения многоканальных оптических корреляторов /12,13/.
1. Голографические методы мультипликации
Все голографические методы мультипликации изображений (или их спектров) основаны на явлении дифракции световых волн, несущих информацию об единичном изображении на периодических структурах оптических масок, полученных путем регистрации голограмм точечных источников.
- 139 -
Эта общность голографических методов мультипликации позволяет дать их формальное описание с помощью линейных операторов m1[s] и m2[s]:
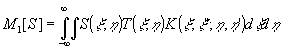 (1) (1)
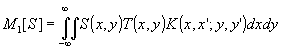 (2} (2}
где s(x,у) - мультиплицируемое изображение; s(x
,h
) - преобразование Фурье или Френеля изображения s(x,у); t(x,у) и t(x
,h
) - амплитудные коэффициенты пропускания мультиплицирующих голографических масок; k(х,x';у,y') и k(x
,x
';h
,h
') - импульсные реакции отображающих оптических систем.
Оператор m1[s] описывает способы формирования идентичных изображения, а оператор m2[s] - способы формирования идентичных спектров. Следует пояснить, что под идентичностью мультиплицированных изображений или их спектров понимается равенство модулей комплексных амплитуд. Это оправдано тем, что все реальные приемники оптического излучения чувствительны только к интенсивности света.
В зависимости от размещения Т( x,у) или Т(x
,h
) в сочетании с другими оптическими элементами можно получить как совокупность идентичных изображений, так и совокупность их пространственных частотных спектров. В таблице 1 приведены схемы получения мультиплицирующих голограмм Т(x,у), схемные реализации операторов m1[s] и m2[s].
Пользуясь рисунками таблицы 1, рассмотрим следующие методы мультипликации.
1. метод голограммы Фурье (метод d
-функций)
Этот метод, основанный на использовании фильтрующего свойства d
-функции *
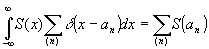 (3) (3)
* Одна переменная используется для сокращения записи.
- 140 -
Таблица 1
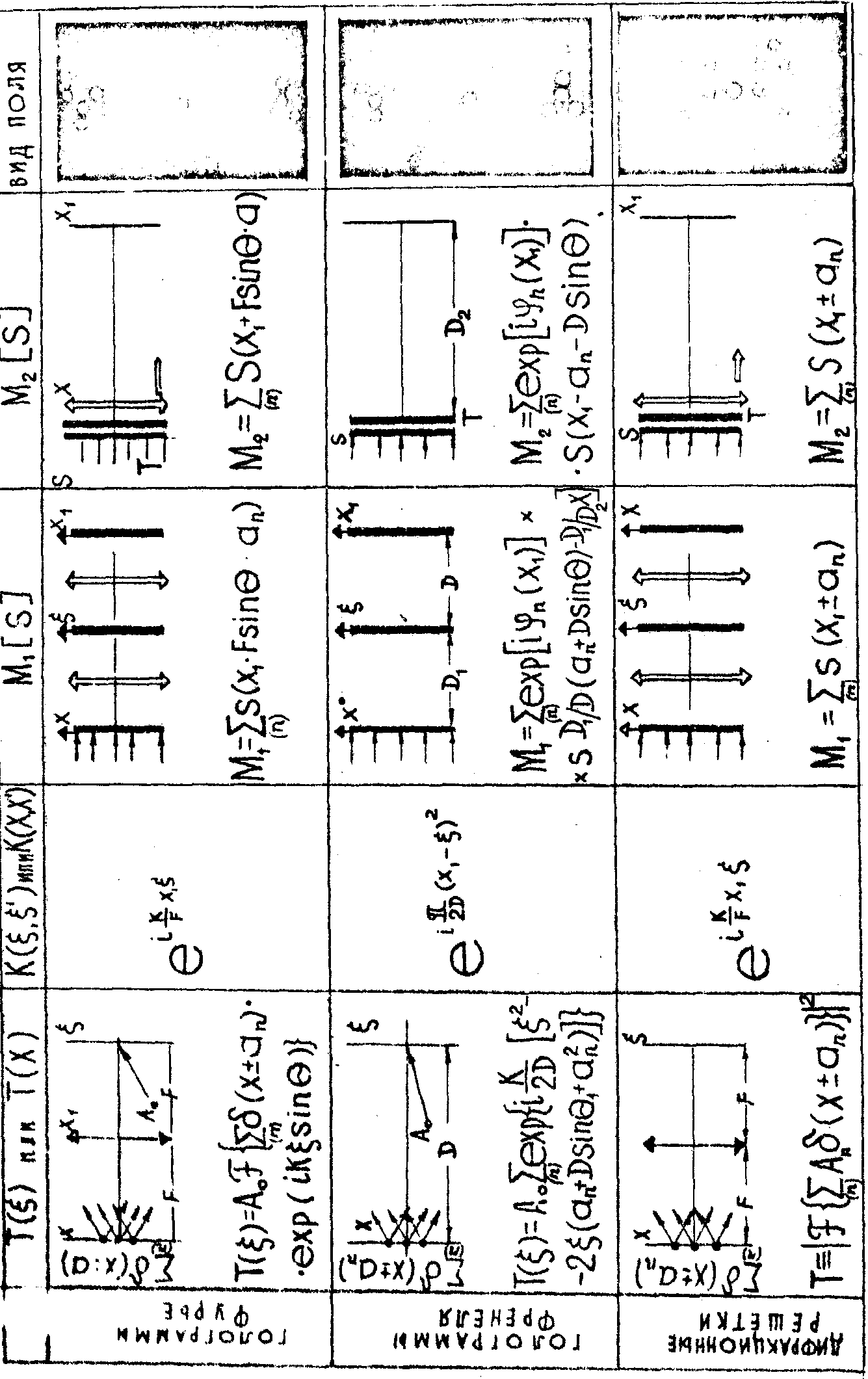
- 141 -
где an - определяется линейными размерами s(x), непосредственно по формуле (3) в когерентной оптической системе реализовать невозможно, поэтому практически мультипликация изображений осуществляется путем перехода к спектральному представлении функции s(x) и 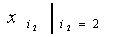 и комбинированию оптических элементов таким образом, чтобы реализовать оператор М1 или М2. и комбинированию оптических элементов таким образом, чтобы реализовать оператор М1 или М2.
Если считать, что в (1) s(x
)=f{s(x)}, a t(x
)=g*n(x
)=f*{gn} *, то при выборе k(x
,x
')=exp(i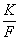 x1x
) легко формируется оптическая схема, в которой реализуется оператор М1 x1x
) легко формируется оптическая схема, в которой реализуется оператор М1[s] в виде
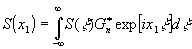 (4) (4)
Хорошо известно, что (3) и (6) эквивалентны, a g*n(x
) входит в одно из слагаемых в выражении для коэффициента пропускания голографической маски,
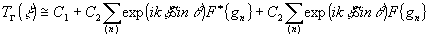 (5) (5)
где sinq
- угол наклона опорной волны, изготавливаемой в схеме, представленной в таблице 1 (квадрат 11) **.
а) Мультипликация изображений
В схеме (квадрат 13) используются 2 одинаковые тонкие линзы, а транспарант с записью s(x), голографическая маска ТГ(x
) и плоскость наблюдения расположены в фокальных плоскостях линз (условно показаны контурной стрелкой). Тогда распределение светового поля в плоскости (х1) при освещении s(x) плоской волной описывается выражением
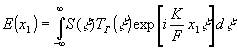 (6) (6)
При подстановке в (6) формулы (5) после несложных преобразований можно показать, что в плоскости (х1) формируются 2n идентичных изображений:
* f - символ преобразования Фурье.
** Набор d
-функций имитируется с помощью линз малого диаметра.
- 142 -
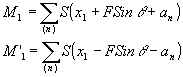 (7) (7)
симметрично смещенных относительно оптической оси системы на f×
sinq
(квадрат 14).
При условии, что центр изображения s(x) находится в точке (x=0) *, положения центров мультиплицированных изображений в плоскости (x1) определяются величинами
x1n = -an-f×
sinq
x'1n = a×
n+ f×
sinq
(8)
Для того, чтобы мультиплицированные изображения не перекрывались, должны выполняться условия
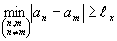
где ℓx - линейный размер изображения s(x).
б) Мультипликация спектров
Если в схеме (квадрат 14) контактно с s(x) установить голограмму ТГ в передней фокальной плоскости линзы, то легко показать, что при освещении s(x}×
ТГ параллельным пучком в плоскости наблюдения формируются две группы спектров;
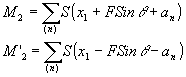 (9) (9)
рассеянных по пространству.
* В дальнейшем считаем, что данное условие выполняется.
- 143 -
Учитывая параметры оптики, размеры входного изображения, максимальную пространственную частоту в изображении, можно определить условия, при которых мультиплицированные спектры не перекрываются.
При другом размещении s(x}×
ТГ в схеме (вплотную к линзе или после нее) формируются спектры вида
 (10) (10)
которые отличаются от (9) квадратичным фазовым множителем y
n(x 1) .
2. Метод голограммы Френеля
Этот метод, подробно рассмотренный в /8/, отличается от метода /7/ использованием плоской опорной волны при изготовлении голограммы, что и обеспечило ему отмеченные ранее преимущества.
При использован оптической схемы квадрата 21 изготавливается голограмма Френеля *:
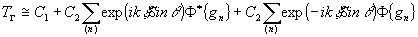 (11) (11)
которая применяется в схемах мультипликации в качестве мультиплицирующего элемента. Таким образом, голограмма Френеля точечных источников представляет собой наложение зонных пластинок Френеля. Она как бы имитирует систему перекрывающихся положительных линз, каждая из которых действует независимо. С помощью реальных линз создать аналог подобной голограммы невозможно.
а) Мультипликация изображений
Рассмотрим схему, показанную в квадрате 25 таблица 1. Если транспарант s(x) освещается параллельным пучком, распространяющимся вдоль оптической оси z , а в плоскости (x
) на расстоянии d1 от s(x) установлена маска ТГ, то тогда распределение комплексной амплитуды света на расстоянии d2 от ТГ в плоскости наблюдения (x1) запишется в виде **
* - F
символ преобразования Френеля.
** Символ свертки.
- 144 -
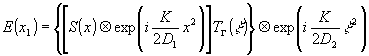 (12) (12)
где 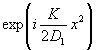 и и 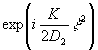 - импульсные реакции свободного пространства. - импульсные реакции свободного пространства.
Рассмотрим случай, когда в схеме выполняется равенство *
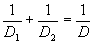 (13) (13)
Тогда при подстановке (11) в (12) и после соответствующих преобразований /8/ распределение для комплексной амплитуды светового поля, определяемой первой суммой из (11), запишется в виде
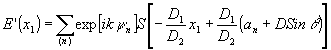 (14) (14)
где 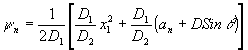 - фазовый множитель. Это означает, что в схеме реализуется оператор (5), причем - фазовый множитель. Это означает, что в схеме реализуется оператор (5), причем
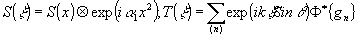
и 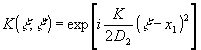
Из (14) видно, что распределение амплитуды светового поля в плоскости (x1) при выполнении условия (13) представляет собой совокупность смещенных распределений, подобных s(x) и отличающихся от него масштабом, зависящим от отношения d1/d2, и фазовыми множителями y
n.
Положение центров мультиплицированных изображений вдоль оси (x1) определяется величинами x1n=d2/d(an+dsinq
).
Это равенство эквивалентно формуле линзы и соответствует условию переноса изображения из плоскости ( x) в плоскость (x1).
- 145 -
Для того, чтобы мультиплицированные изображения не перекрывались, достаточно выполнить условие
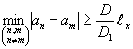
Если подобным образом проанализировать вторую сумму из выражения (12), то можно убедиться в том, что кроме n действительных изображений, фокусирующихся вдоль оси (x1), имеют место n мнимых изображений, которые можно перенести с помощью линзы в удобную для регистрации плоскость.
б) Мультипликация спектров
Вернемся к выражении (12) и положим d2=d (схема квадрата 24). (При этом d, может быть произвольным; в приведенной схеме d1=0). Тогда после преобразований будем иметь
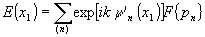 (15) (15)
где
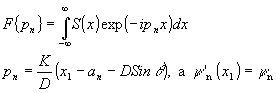
Выражение (15) представляет собой совокупность пространственных частотных спектров Фурье изображения s(x), умноженных на фазовые функции и смещенных относительно оси z. Отметим что при d1=d фазовые функции содержат только линейные члены.
Из (15) следует, что спектры изображений центрируются в точках с координатами
x1 = a×
n+ d×
sinq
а их масштаб определяется величиной k/d.
Условия непересечения спектров выполняются, если
- 146 -
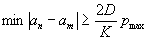
где pmax - высшая пространственная частота в спектре.
Анализ показывает, что если допустимо наличие квадратичных фазовых набегов у спектров Фурье , то, выбирая d1>d, можно получить схему, в которой одновременно формируются как мультиплицированные изображения, так и спектры Фурье - у них будут только различные плоскости фокусировки (для изображений d2=d×
d1/(d1-d), а для спектров d2=d). Иногда удобнее освещать транспарант плоской волной, падающей наклонно, причем угол падения должен быть обратным относительно угла падения волны при записи. Это позволяет исключить сдвиг изображений или спектров, равный f×
sinq
.
3. Метод дифракционных решеток
Сложная двумерная решетка изготавливается в схеме квадрата 31 путем записи на фотоматериале интерференционной картины от n точечных источников. В этом случае оптическая маска с амплитудным коэффициентом пропускания
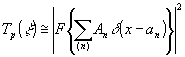 (16) (16)
используется для реализации операторов М, и Л . а) Мультипликация изображений
Если в схеме квадрата 33 транспарант s(x) осветить плоским пучком света (оптические маски s(x), tp и плоскость наблюдения расположены в фокальных плоскостях линз), то на выходе формируются мультиплицированные изображения
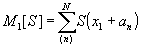 (17) (17)
где 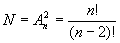 - число изображений. - число изображений.
При изготовлении решеток (16) необходимо предварительно анализировать взаимное расположение линз в матрице, чтобы мультиплицированные изображения в плоскости регистрации не перекрывались.
- 147 -
Их расположение можно определить с помощью графического построения.
Предположим, что для регистрации дифракционной решетки используется матрица из четырех линз, расположенных так, как показано на рис.1а. Определим расположение изображений в плоскости регистрации, воспользовавшись вспомогательным рис.1б.
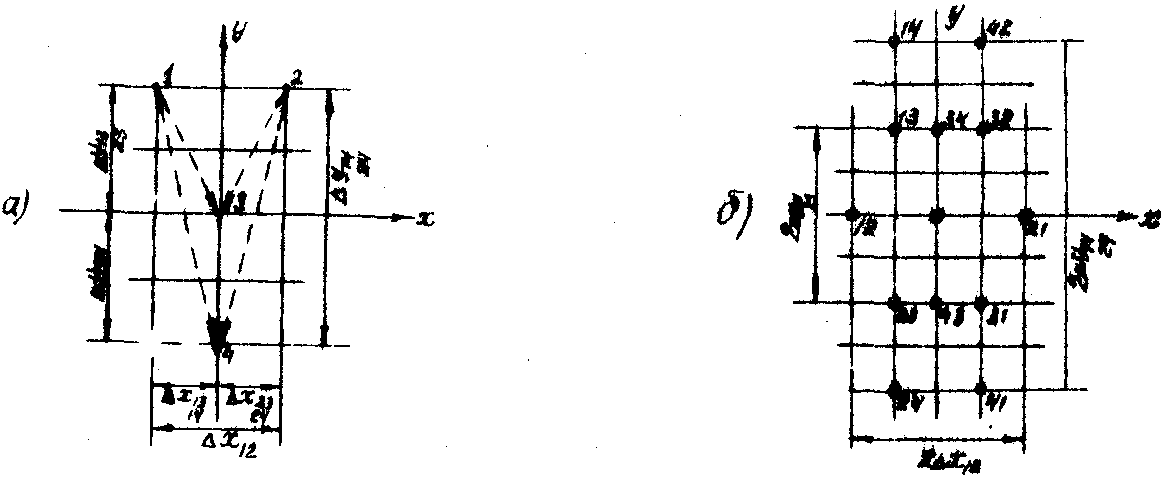
Рис.1. Графическое определение расположения центров мультиплицированных изображений.
Для каждой пары точечных источников (1-2, 1-3, 1-4, 2-3, 2-4, 3-4) определяем численные значения D
x12, D
x13, D
x14, D
x23, D
x24, D
x34 и D
y12, D
y13, D
y14, D
y23, D
y24, D
y34, равные расстояниям между проекциями точечных источников на оси x и y, соответственно. Полученные значения D
x и D
y откладываются по обе стороны относительно нуля по осям Х и y и параллельно им проводятся прямые. В точках пересечения параллельных прямых от одной пары источников будут располагаться "оптические центры тяжести" мультиплицируемых изображений. Так как точек пересечения прямых от одной пары источников (например, 2D
x12, и 2D
y12) четыре, то на выбор двух нужных указывает направление вектора, соединяющего источники. В случае увеличении количества точечных источников определение расположения изображений производится аналогично. Для того, чтобы мультиплицированные изображения не перекрывались, должны выполняться
- 148 -
условия D
xkℓ-D
xkm³
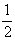 ℓx, а все мультиплицированные изображения находились в плоскости (x1) необходимо выполнение условий D
xkℓmax<dL
(dL
- диаметр преобразующих линз). ℓx, а все мультиплицированные изображения находились в плоскости (x1) необходимо выполнение условий D
xkℓmax<dL
(dL
- диаметр преобразующих линз).
б) Мультипликация спектров
С помощью tp в схеме квадрата 34 легко формируется совокупность идентичных спектров m1=s(x1+an}. Если маска s(x)×
tp расположена не в фокальной плоскости преобразующей линзы, то появляются дополнительные фазовые множители, которые при необходимости могут быть определены.
Поскольку в литературе данных по таким решеткам не приводилось, то нам представлялось интересным оценить зависимость дифракционной эффективности от времени экспозиции (Но ) и числа точечных источников (n).
На рис.2 приведены эти зависимости, полученные расчетным путем по методике /11/ для фотопластинок crwolp-1.
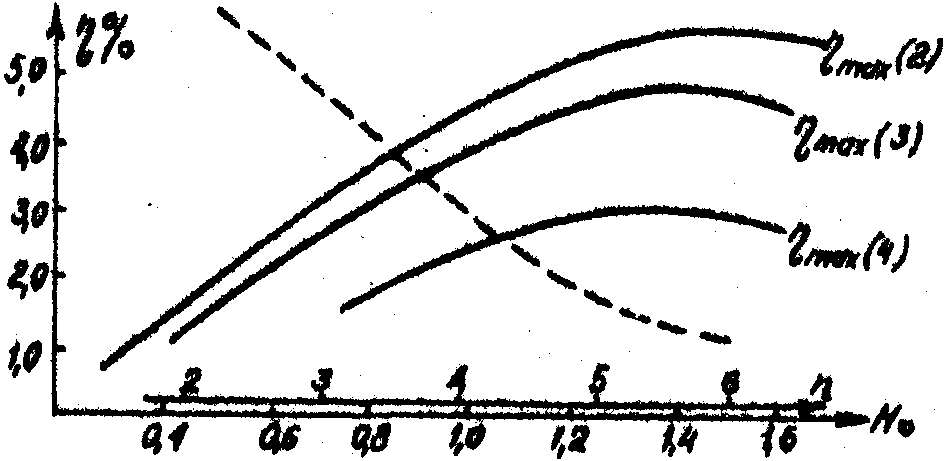
Рис.2. Зависимость дифракционной эффективности решеток от времени экспозиции и числа точечных источников.
Из рис.2 видно, что при фиксированных n дифракционная эффективность h
в широком интервале изменения Но меняется незначительно, но сильно зависит от числа точечных источников в интервале от 2 до 6, а затем изменяется слабо (при фиксированной Но).
- 149 -
ii. Мультипликация изображений с помощью простых фазовых решеток
Профиль такой решетки показан на рис.3а, где D
- глубина травления, d - период решетки, q
- угол дифракции в плоскости Х, n - показатель преломления.
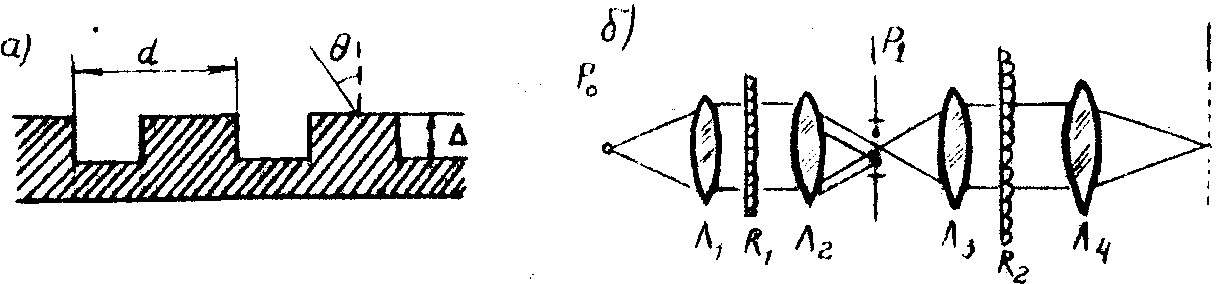
Рис.3. а) профиль дифракционной решетки,
б) двухкаскадная схема мультипликатора.
Используя теорию простых фазовых решеток, приведенную в /10/, можно показать, что отношение интенсивности мультиплицированного изображения в дифракционном порядке (К,ℓ) к полной интенсивности света, падающего на решетку i0, будет
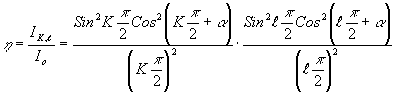 (18) (18)
Отсюда видно, что в плоскости мультиплицированных изображений не содержится изображений четных порядков, а интенсивность счетных порядков существенно меньше интенсивности изображений порядков 0,0; 0,1; 1,1.
На рис.4 показаны кривые для h
о,o; h
о,1; h
1,1. При значении a
=1,004 h
о,o; h
оo= h
о1=h
11 простая фазовая решетка прямоугольного
- 150-
профиля мультиплицирует девять изображений одинаковой интенсивности.
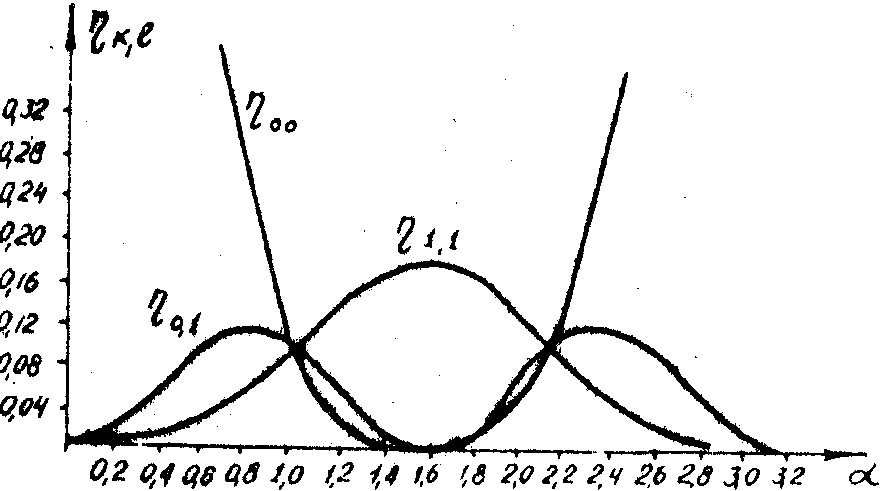
Рис.4. Зависимость эффективности фазовой решетки от параметра a
.
Схема оптической системы мультипликации показана на рис.5б. Изображение или его пространственный спектр проектируется на опаловое отекло. В плоскости Р 1 формируются 9 изображений одинаковой яркости, идентичных входному. В этой плоскости для отсечки слабых изображений более высоких порядков ставится диафрагма. Картина в плоскости Р1 служит входным изображением для следующего каскада. Таким образом, на выходе второго каскада в плоскости мы получим 81 изображение одинаковой яркости, идентичных изображению в плоскости Р0. В принципе можно увеличивать число каскадов, однако интенсивность мультиплицированных изображений быстро падает. Однако, выбирая различные значения параметра a
, т.е. различную глубину травления, мы можем добиться перераспределения энергии в различных порядках. Например, если мы ходим в двухкаскадной схеме получить не 81, а 16 изображений, но с максимально возможной эффективностью, то нам следует выбрать a
»
1,6. В этом случае используются только изображения порядка 1,1.
Недостатком такого метода мультипликации является искажение
-151 -
изображений. Рассмотрим их качественно. На рис.5 показан один каскад мультипликатора.
Для точки изображения, отстоящей на расстоянии r от оптической оси системы, условия образования главных максимумов запишутся
sinq
-sinj
=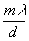 (19)
а для осевой точки
sinq
=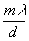 (20)
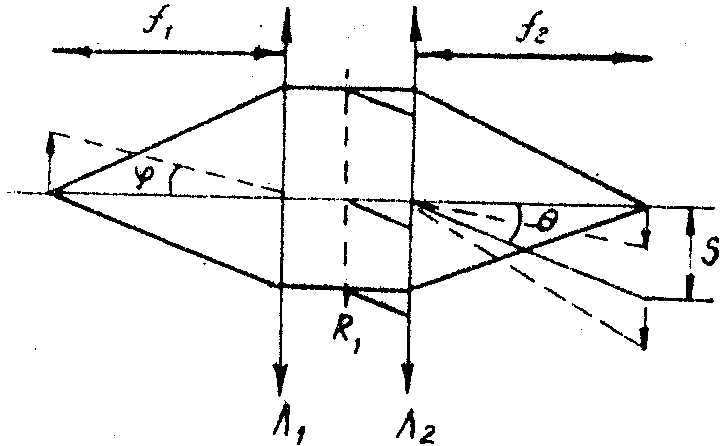
Рис.5. Рисунок, поясняющий характер искажений, вносимых дифракционной решеткой.
Расстояние между центрами мультиплицированных изображений в плоскости Р 1 будет
s = ¦
2tgq
(21)
причем q
здесь определяется из условия (20). В то же время расстояния между краями мультиплицированных изображений, как это следует из (19), будет отличаться от величины s. Это говорит о том, что изображения в первых порядках будут искажены. Причем, эти искажения будут тем больше, чем больше угол q
. В /10/
- 152 -
показано, что для малых искажений необходимо выбирать решетки, у которых q
=6¸
8°, а это ограничивает величину периода решетки, поскольку в этом случае d>(l
/0.1). С другой стороны, величина периода решетки ограничена требуемым размером мультиплицированных изображений, так как для больших изображений расстояние между ними должно быть не меньше чем их размер, а увеличение расстояния s требует увеличения угла q
и, следовательно, уменьшения a
.
iii. Мультипликация изображений с помощью оптического туннеля
Оптический туннель, представляющий собой полый параллелепипед, внутренние грани которого являются зеркально отражающими поверхностями, позволяет реализовать простой мультипликатор изображений и их пространственных спектров, работающий как в когерентном, так и в некогерентном свете /12,13/.
Процесс мультипликации изображения основан на том, что световые лучи, исходящие из отдельных точек изображения, претерпевают последовательные отражения в системе из четырех зеркал. Это приводит к образованию ряда мнимых изображений, которые переносятся объективом в плоскость изображений.
Ход лучей в оптическом туннеле определяется углами q
и j
(рис.6). Будем называть изображением порядка k,ℓ мнимое изображение точечного источника, которое образуется лучами, претерпевшими k отражений от горизонтальных и ℓ отражений вертикальных граней туннеля.
Рассматривая ход лучей в оптическом туннеле, можно показать, что отношение интенсивности мнимого изображения порядка k,ℓ к интенсивности входного изображения будет
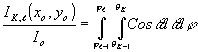 (22) (22)
где
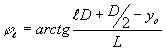 (23) (23)
- 153 -
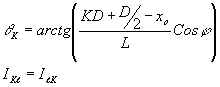 (23) (23)
d - ширина оптического туннеля, l - длина оптического туннеля, x0 и y0 - координаты светящейся точки в плоскости апертуры туннеля.
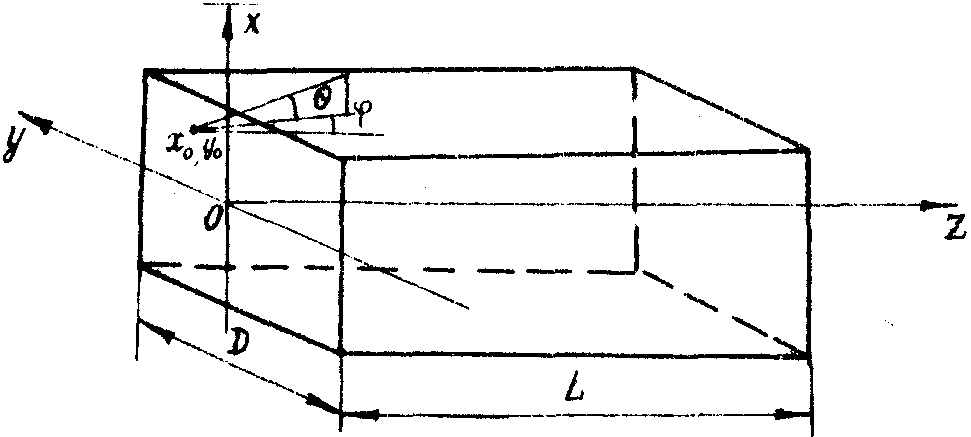
Рис. 6. Оптический туннель.
По формуле (22) (при x0=0, y0=0) были получены графики зависимости ik,ℓ/i0 от параметра оптического туннеля a=d/l, показанные на рис.7.
При расчете ik,ℓ/i0 параметр а варьировался от 0 до 1, поскольку оптические туннели при а>1 не имеют практического значения. Существенные отличия в яркости изображений различных порядков при значениях а>0.25 приводят к тому, что оптические туннели с такими значениями а становятся малопригодными для построения многоканальных устройств обработки изображений с большим числом каналов.
Поэтому для построения мультипликаторов изображений наиболее приемлемыми являются туннели, у которых параметр а находится в пределах 0.05 < а < 0.25. В этом случае отличия в яркости изображений различных порядков значительно меньше, чем для
- 154 -
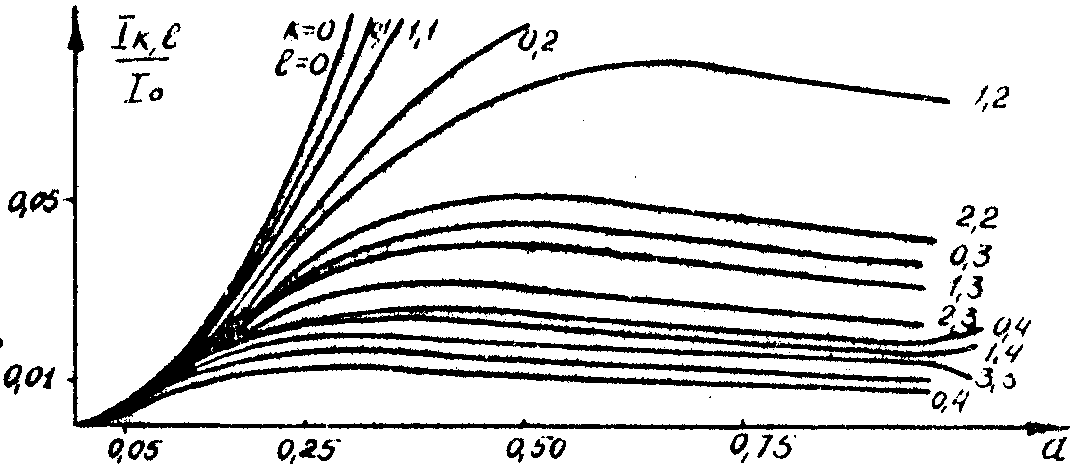
Рис.7. Зависимости энергетических показателей оптического туннеля от параметра а .
случая а > 0,25. Существенно, что при малых а сравнительно просто получить изображения одинаковой яркости. Для этого можно использовать выравнивающую маску, представляющую собой фотопластинку, проэкспонированную на линейном участке характеристической кривой фотоносителя.
Из рис.7 видно, что для 81 изображения (это предполагает использование изображений до четвертого порядка включительно) интенсивность слабейшего из них при и а = 0.1 достигает 1% от интенсивности входного изображения. Помимо неодинаковой яркости мультиплицированных изображений, другим недостатком туннельного мультипликатора является зависимость ik,ℓ от координат точки x0, y0 во входной плоскости. Это, вообще говоря, приводит к искажению функции яркости В(x,у) мультиплицированных изображений. Однако, анализ показывает, что при малых a (больших l) функция яркости изображения передается оптическим туннелем практически без искажений.
Максимально достижимое число изображений в мультипликаторе, схема которого приведена в /13/, зависит от угла зрения объектива. Чтобы уменьшить искажения изображений в различных порядках из-за виньетирования наклонных пучков, необходимо применять специальные объективы и использовать оптические туннели с малым
- 155 -
значением а.
Заключение
Проведенное рассмотрение методов мультипликации не является исчерпывающим. Целью этого доклада явилось изложение некоторых свойств оптических мультиплицирующих элементов, важных с точки зрения их использования в многоканальных устройствах обработки изображений.
Литература
1. p.a.newman, v.e.rible. appl.optics, v.5, p.1225,1966.
2. w.i.tabor. appl.optics, v.6, p.1275, 1967.
3. r.s.eng. appl.optics, v.8, р.2117, 1969.
4. a.i.carswell. appl.optics, v.8, p.712, 1969.
5. Лу-Сунь, ТИИЭР т.56, стр.132. 1968.
6. h.w.hemstreet et. al. iosa, v.59, p.1544a, 1969.
7. g.groh. appl.optics, v.7, p.1643, 1968.
8. А.С.Блок и др. "Оптика и спектроскопия", т.xxxiii, вып.1, стр.149, i972.
9. s.c.som. iosa, v.6o, p.1628. 1970.
10. l.p.boivin. appl.optics, v.11, n 8, 1972.
11 . Э.И.Крупицкий, И.С.Барбанель. "Оптика и спектроскопия", т.xxxiii, вып.6, 1972.
12. А.С.Блок, Л.П.Карпов. Труды НТК ЛЭИС, вып.1, 1970.
13 . Э.И.Крупицкий, Л.П.Карпов и др. А.с.№ 307411, бюлл.изобр.№ 20, 1971.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

