|
|
 |
 |

|
| |
ИНТЕРФЕРОМЕТРЫ ИНТЕНСИВНОСТИ В ГОЛОГРАФИИ
П.Г.Власов
Интерференционные эффекты, наблюдаемые визуально в оптическом диапазоне, являются проявлением корреляции волнового поля по амплитуде. Анализ последних работ по когерентной оптике и голографии показывает однако, что могут наблюдаться интерференционные эффекты, соответствующие корреляции более высокого порядка-корреляции по интенсивности.
Прежде чем приступить к их непосредственному описанию, рассмотрим кратко основные свойства излучения, которые, следуя ряду работ зарубежных авторов, целесообразно охарактеризовать, как диффузно-когерентное .
В классической интерферометрии применяются тепловые источники, при описании которых комплексная амплитуда оптического волнового поля рассматривается как реализация стационарного случайного процесса, зависящего от времени /1/. Однако, в системах когерентной оптики и голографии используется когерентное лазерное излучение и временная зависимость может не учитываться /2/, т.к. разность фаз между колебаниями в двух произвольно взятых точках наблюдения во времени не изменяется. С другой стороны, исследование диффузно-отражающих или рассеивающих объектов, освещенных когерентным излучением, а также применение диффузных рассеивателей, становящихся сейчас фактически новым оптическим элементом в когерентной оптике и голографии приводит к тому, что комплексная амплитуда становится случайной функцией не времени, а координат. Действительно, микроструктура поверхности диффузного рассеивателя описывается как реализация стационарного случайного процесса, зависящего от пространственных координат и обладающего свойством эргодичности, математическое ожидание которого постоянно, а для рассеивателя с плоской поверхностью эта постоянная равна нулю.
- 125 -
При освещении диффузного рассеивателя когерентным излучением, информация о поверхностной микроструктуре, размеры которой превышают длину волны, переносится на прошедшее или отраженное излучение /3/. Таким образом, случайные свойства диффузного рассеивателя переносятся на освещающее его излучение, а затем и на изображение объекта, созданное оптической системой или голограммой. Подробное рассмотрение статистических свойств изображения объекта при диффузно-когерентном освещении можно найти в работах /4,5/. Случайная зависимость волнового поля от пространственных координат проявляется, в частности, в образовании зернистой (гранулярной) структуры как в плоскости изображения, так и в любой промежуточной плоскости оптической системы. Образование зернистой структуры можно наблюдать визуально в простом демонстрационном эксперименте (рис.1а). Нерасширенный луч лазера проходит через диффузный рассеиватель - матовое стекло и на расстоянии около метра от него на экране наблюдения отчетливо видна дифракционная картина, состоящая из отдельных зерен (гранул), образованная в результате интерференции излучения, прошедшего через различные рассеивающие центры матового стекла. Обычно принимается следующая модель освещенного диффузного рассеивателя /6/: считается, что он состоит из точечных источников, излучающих с равной амплитудой и случайной фазой, изменяющейся от источника к источнику в интервале от -p
до +p
. В плоскости наблюдения суммарная амплитуда также изменяется случайным образом (рис.1б по работе /7/), что и приводит к образованию зернистой структуры, средний размер зерен которой пропорционален расстоянию от диффузного рассеивателя и обратно пропорционален размеру его освещенного участка. Средний размер зерен в плоскости изображения оптической системы определяется ее разрешением и равен 1,2l
f/d, где d - действующий диаметр объектива. Этот результат легко может быть понят в терминах радиотехники при прохождении белого шума (излучения после диффузного рассеивателя) через линейный фильтр (оптическая система или свободное пространство), функция корреляции на выходе совпадает с импульсным откликом фильтра /9-10/.
Зернистая структура образована излучением, прошедшим или отразившимся от диффузно рассеивающей поверхности и, следовательно,
- 126 -
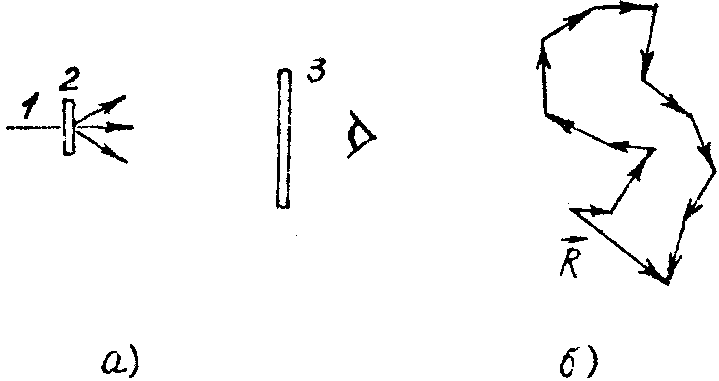
Рис.1. Демонстрационный эксперимент по наблюдению зернистой структуры диффузно-когерентного излучения:
а) схема эксперимента: 1 - луч лазера, 2 - диффузный рассеиватель, 3 - экран наблюдения, 4 - глаз наблюдателя;
б) пример возможной диаграммы образования суммарной амплитуды в одной из точек плоскости наблюдения. Интенсивность равна 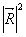 . .
она несет информацию как о волновом фронте и когерентности освещающего излучения, так и о форме, микроструктуре и размере освещенного участка объекта /11/. Определение размеров микроструктуры на основе этого эффекта описано в /12/, a в /13,14/ предложен и экспериментально подтвержден способ определения длины когерентности лазерного излучения по контрасту зернистой структуры. Не разбирая эти работы, ограничимся в дальнейшей основным применением - интерференционными измерениями.
Первые эксперименты по наблюдению интерференционной картины, образованной наложением двух зернистых структур, опубликованы в начале 1968 г. /15/. Расширенный луч лазера проходил через диффузный рассеиватель, на расстоянии одного см, от которого помещалась
- 127 -
фотопластинка. Фотопластинка многократно экспонировалась, смещаясь между экспозициями на заданную величину микрометрическим винтом. После фотообработки и преобразования Фурье набора случайных дифракционных картин, зафиксированных на фотопластинке, в фокальной плоскости линзы, производящей преобразование Фурье, наблюдалась отчетливая интерференционная картина. Рассмотрим подробнее механизм ее образования для случая двойной экспозиции. Амплитудное пропускание Т ( x,у) проявленной фотопластинки равно:
t(x,y) = 1-a
t{j(x,y)+j(x+D
x,y)} (1)
где a
- постоянная для малых экспозиций, t - время экспозиции, j(x,у) и j(x+D
x,y)- интенсивность, падающая на фотопластинку во время первой и второй экспозиции, соответственно. Найдем распределение амплитуд в фокальной плоскости линзы, производящей преобразование Фурье, пользуясь известными свойствами этого преобразования:
f[t(x,y)] = d
(w
)-a
t(1+eiw
D
x)f[j(x,y)] (2)
В (2) f[] - символическое обозначение преобразования Фурье, d
(w
) - дельта функция, w
=2p
x¦
/l
- пространственная частота, x¦
- координаты в плоскости частот (фокальной плоскости линзы). d
(w
) - описывает светящуюся точку в фокальной плоскости линзы, образованную излучением, прошедшим фотопластинку без рассеяния. Считывая далее только второй член в (2) и имея в виду, что преобразование Фурье от квадрата модуля функции |
u(x,y)|
2=j(x,y), где u(x,у) - комплексная амплитуда равно автокорреляции ее Фурье-образа, получим
f[t(x,y)] = g(w
)(1+eiw
D
x) (3)
В (3) g(w
) - взаимный энергетический спектр. Глаз наблюдателя или любой квадратичный детектор, помещенный в фокальную плоскость, зарегистрирует интенсивность
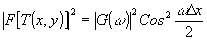 (4) (4)
- 128 -
Таким образом, измеряя контраст интерференционных полос, можно найти значение нормированного квадрата модуля взаимного энергетического спектра. Описание экспериментов по наблюдению интерференционной картины от наложения зернистых структур можно найти также в /16/.
Проанализируем теперь работу /15/ с иной точки зрения, сделав несколько неожиданное, на первый взгляд, сравнение описанного в /15/ устройства с интерферометром интенсивности Х.Брауна-Твисса /17/, в котором излучение теплового источника принимается вначале двумя квадратичными детекторами, разнесенными в пространстве. Выходы обоих приемников после низкочастотного фильтра подаются на коррелятор, где производится перемножение сигналов и усреднение по времени в интегрирующей цепочке. В описанном выше эксперименте случайная дифракционная картина записывалась на фотопластинке, также являющейся квадратичным детектором. Двум детекторам, разнесенным в пространстве, соответствует двойная экспозиция со смещением фотопластинки между экспозициями. Для устранения влияния зернистой структуры, составляющей микроструктуру интерференционной полосы, контраст последней измеряется, как интегральная величина /18/, усреднением по пространственной координате вдоль полосы. Для получения полной зависимости |
g(w
)|
2 от величины смещения необходимо замерить контраст полос в серии измерений с различными смещениями, что соответствует изменению расстояния между квадратичными детекторами в интерферометре Х.Брауна-Твисса. Отметим два основных, но не принципиальных отличия описанного интерферометра интенсивности от своего классического аналога. Первое вызвано тем, что диффузно-когерентное излучение является случайной функцией не времени, а координат, поэтому усреднение по времени заменяется усреднением по пространству, второе - измерением непосредственно |
g(w
)|
2, a не нормированного коэффициента корреляции по амплитуде. Как будет показано ниже, второе отличие в ряде случаев полностью исчезает.
Как и в любом интерферометре, в описанном интерферометре интенсивности по контрасту интерференционных полос исследуются корреляционные свойства излучения, а по форме полос изменения происшедшие с объектом. Исследования корреляционных свойств диффузно-когерентного излучения на основе этого метода пока только начинаются /19/,
- 129 -
а большинство работ посвящено исследованию деформаций, вибраций и малых смещений диффузно-отражающих объектов. Все точки объекта вносят вклад в зафиксированную на фотопластинке интенсивность дифракционной картины, поэтому по ее изменению можно определить только интегральную величину изменения, происшедшего с объектом. Для определения локальных изменений необходимо сфокусировать на фотопластинку изображение объекта /20,21/ (рис.2). По схеме на рис.2 поверхность исследуемого объекта освещается симметрично
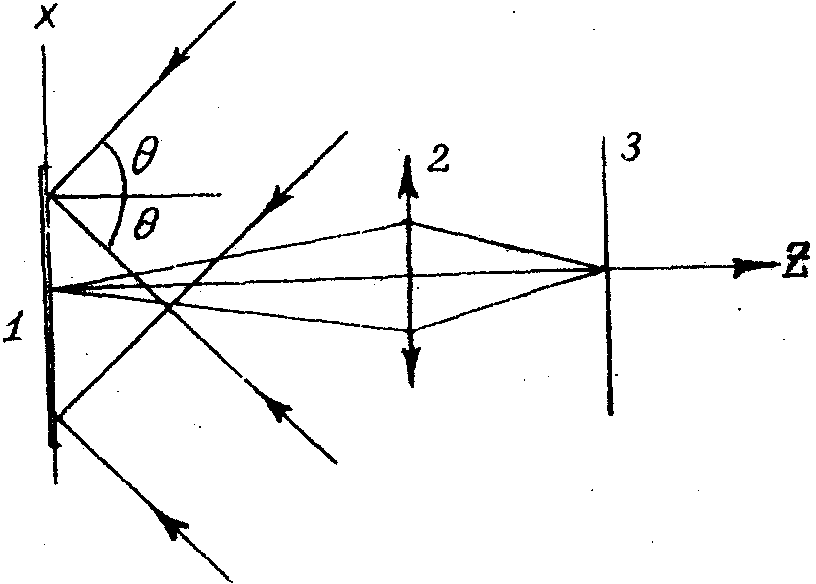
Рис. 2. Схема получения интерферограммы интенсивности при двухстороннем освещении объекта.
1 - объект, 2 - линза, 3 - фотопластинка.
двумя когерентными пучками лазерного излучения. Пучки расположены под углами q
и -q
к оси z и перпендикулярны к оси y. Поверхность фотографируется, проявленная фотопластинка возвращается на прежнее место, после чего объект подвергается деформации или вибрации. Из рис.2 видно, что смещение поверхности по z или y направлениям не изменяет зернистой структуры в плоскости изображения. Как показано в /20,21/, смещение поверхности по направлению x на величину dx приводит к появлении в функции, описывающей пропускание фотопластинки, интерференционного члена, пропорционального 1+cosd
, где d
- разность фаз, равная 4p
sinq
/l
. Таким образом, фотопластинка покрывается интерференционными полосами,
- 130 -
образующими контуры равных сечений по оси Х . Если поверхность освещена с одной стороны под углами q
1 и q
2, метод становится чувствителен и к смещению по оси z, т.к. в этом случае 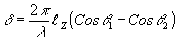 , где ℓz - смещение по оси z. Метод двойной экспозиции, в том числе с однопучковым освещением поверхности, обсужден в /8/. , где ℓz - смещение по оси z. Метод двойной экспозиции, в том числе с однопучковым освещением поверхности, обсужден в /8/.
Интерферометр другого типа, изображенный па рис.3, напоминает модифицированный интерферометр Майкельсона, в котором отражающие зеркала заменены диффузно-отражающими поверхностями /20-22/. Линза, помещенная после полупрозрачного зеркала, образует совмещенные изображения поверхностей на фотопластинке, возвращенной после фотообработки на прежнее место. Одна из поверхностей неподвижна и является опорной. Интерференционные полосы, образующиеся при изменении другой поверхности, наблюдаются при помощи линзы, позволяющей видеть сразу все плоскости изображения. В этом интерферометре чувствительность к смещению по осям Х и y на порядок меньше, чем к смещений по оси z.
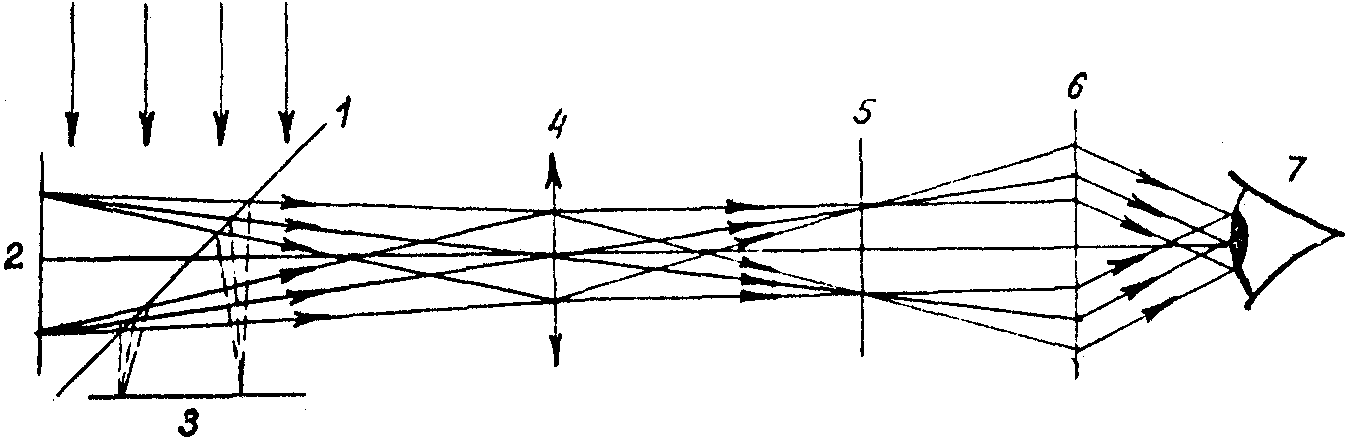
Рис.3. Схема интерферометра с эталонной диффузно-отражающей поверхностью. 1 - делитель пучка, 2,3 - диффузно-отражающие поверхности, 4-6 - линзы, 5 - фотопластинка, 7 - глаз наблюдателя.
Как и в голографической интерферометрии, возможно исследование методом усреднения по времени, однако в отличие от голографической
- 131 -
интерферометрии усреднение приводит не к появлению интерференционной картины, а к размытию зернистой структуры, которая сохраняется только в местах узлов вибраций /23,24/. Для ее визуального наблюдения размеры зерен в плоскости изображения могут быть сделаны достаточно большими за счет малой апертуры оптической системы, создающей изображение объекта. Различные конструкции таких интерферометров, их возможности и методические вопросы обсуждаются в /25,26/. Интерференционные полосы можно получить, применяя стробоскопирование /7,27/.
Сравним описанные методы исследования диффузно-отражающих объемов с методами голографической интерферометрии. Регулируемый размер зерен зернистой структуры позволяет использовать для регистрации обычные фототехнические эмульсии. Можно обойтись вообще без фотопроцесса, устанавливая при помощи апертуры средний размер зерен в плоскости изображения таким, чтобы он был разрешен обычным промышленным видиконом /7,2/, передающим изображение из 350х 170 точек. Интерференционная картина, соответствующая измененным состоянием объекта, наблюдается тогда в реальном масштабе времени на экране телевизора. Снижаются требования и к виброзащите установок. По сравнению с голографической интерферометрией, наряду с перечисленными преимуществами, существует ограничение класса исследуемых объектов. Так как в процессе измерения участвуют линзы, метод применим только к объектам с плоской поверхностью. Для объектов с криволинейной поверхностью может быть измерена только интегральная величина деформаций, смещений, вибраций и других изменений, приводящих к отклонению поверхности объекта от первоначального положения.
В заключение отметим, что изложенные выше применения интерферометров интенсивностей в диффузно-когерентном излучении, вероятно, далеко не исчерпывают всех их возможностей, которые пока полностью не исследованы.
- 132 -
Литература
1. М.Борн, Э.Вольф. Основы оптики. М., "Наука", i970.
2. Л.Сороко. М., УФН, 90, № 1, 7. 1967.
5. d.gabor. progress in optics, 1, 109, 1961.
6. .c.dainty. opt.acta, 17, 11, 761, 1970.
5. s.lowenthal, h.arsenault. josa, 60, 11, 1970,
6. l.i.goldfisher. josa, 55, 3, 247, 1965.
7. j.n.butters, j.a.lenderts. opt. and laser techn., 26-30, 1970.
8. e.archbold, j.m.burch, a.e.ennos. opt.acta, 17, 12, 883, 1970.
9. В.И.Тихонов. Статистическая радиотехника. М., "Сов.радио", 1966.
10. Б.Р.Левин. Теоретические основы статистический радиотехники. М., "Сов.радио", 1965.
11. g.groh.. "engineering uses of holography 1968", p. 483, 1970.
12. r.b.grane. josa, 60, 12, 1658, 1970.
13. f.m.motier, r.dandliker. opt. commun., 3, 5, 366, 1971.
14. r.dandliker, f.m.motier. z. and. math. und phys., 22, 5, 369, 1971.
15. j.m.burch, j.u.tokarski. j.optica acta, 15, 2, 101, 1968.
16. s.debrus at all, opt. instrum. and techn., 1969, p.37, 1970.
17. В.И.Слыш. УФН, 87, № 3, 47i-489, 1965.
18. l.h.tanner. j.sci.instrum., s2, 1, 517, 1968.
19. s.debrus, c.p.grover. opt. commun., 3, 5, 340, 1971.
20. j.a.lenderts. opt. instrum. and techn., 1969, р.256, 1970.
21. j.a.lenderts. j.sci.instrum., 3, 214, 1971.
22. t.nakajima. jap.j.appl.phys., 10, 3, 394, 1971.
23. e.archbold, j.m.burch, p.a.taylor, a.e.ennos. nature, 222, 263, 1969.
- 133 -
24. e.archbold, a.e.ennos, p.a.taylor. opt.instrum. and techn., p.41, 1970.
25. k.a.stetson. opt. and laser techn., 2, 4, 179. 1970.
26. b.elliason, f.m.motier. j0sa, 61, 5, 559, 1971.
27. j.a.lenderts. phys.bull., 22, 393, 1973.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

