ТЕ0РЕТИЧЕСКИЕ ОСНОВЫ ГОЛОГРАФИИ НЕСТАЦИОНАРНЫХ ПРОЦЕССОВ
В.А.Зубов
В работе рассматривается метод голографической регистрации, основанный на использовании специально сформированной опорной волны. Запись сигнала
e0(t)=e
(t)exp[-iw
t] осуществляется с опорной волной с линейный изменением частоты по сечению. Пропускание полученной голограммы содержит информацию о временном Фурье-образе исследуемого сигнала. Временная картина сигнала может быть восстановлена при использовании волны с теми же характеристиками, что и опорная. Спектральная картина сигнала получается при исключении мешающих составляющих из зарегистрированного на голограмме спектра. Оптическая обработка информации, содержащейся на голограмме, позволяет подучить фазовые характеристики исследуемого сигнала.
Большинство известных в настоящее время способов регистрации нестационарных процессов основано на быстрой регистрации последовательности статических голограмм и восстановлении неподвижных образов /1/. Эффект движения достигается за счет последовательного воспроизведения дискретного набора статических образов
/2/. Другой подход состоит в регистрации голограмм в специальных условиях, при которых перемещения объекта не ухудшают четкости статического восстановленного изображения. Это достигается перестройкой частоты опорного излучения в соответствии с изменением из-за аффекта Доплера частоты излучения, рассеянного о6ьектои; перестройка достигается за счет движения отражателя опорного пучка синхронно с движением объекта /3/. Использование быстродействующих затворов, управляемых системой, следящих за
- 111 -
качеством голограммы, позволяет регистрацию голограммы производить в то время, когда она имеет высокий контраст; в те же моменты времени, когда картина размывается, регистрация не производится. Эта система динамической голографии удобна в случае движения объекта к голограмме или от нее /4/.
Третий вариант основан на компенсации дополнительной разности хода, возникающей при движении объекта, за счет смещения опорного светового пучка по плоскости голограммы, причем, требуется знание скорости и траектории движения объекта. Опорная волна и волна, рассеянная объектом, направляются на регистрирующую фотопластинку под близкими углами, смещения объекта должны быть не очень велики /5/. Третий подход состоит в учете эффекта изменения интенсивности излучения, образующего голограмму, за счет фазовой модуляции сигнального пучка. Это сводится к уменьшению контраста голограммы в зависимости от смещения объекта /6/. Все указанные системы позволяют регистрировать только объекты, двигающиеся поступательно и не изменяющие относительного расположения отдельных частей. При восстановлении изображения все эти системы дают статическую, не изменяющуюся во времени, картину. Однако, можно стремиться не к исключению перемещения, а к тому, чтобы с помощью голографии записать сам процесс изменения во времени, и настоящей работе на основе /7,8/ рассматривается способ голографической регистрации нестационарных процессов: способ основан на использовании специально сформированного опорного пучка, причем, запись проводится в непрерывном режиме, а не отдельными кадрами.
Все существующие способы исследования оптических сигналов, как правило, регистрируют какое-либо один вид информации о сигнала. Регистрация спектрального составе осуществляется спектроскопическими методами. Регистрация временной картины основана на принципах механической или электронной развертки. Регистрация информации о фазах сигнала основана на явлении интерференции. Однако, в случае света сложного спектрального состава классические методы не годятся. Главная отличительная особенность рассматриваемого способа записи в том, что регистрируется полная информация о сигнале: информация о временной картине сигнала и информация
- 112 -
о спектральной картине сигнала с одной стороны, информация о распределении амплитуд сигнала и информация о распределении фаз сигнала. В работе будут рассмотрены способы извлечения информации того или иного типа из зарегистрированной картину сигнала.
i.
Запись сигнала
Регистрация временной картины нестационарного процесса выполняется следующим образом (рис.1). Исследуемое излучение
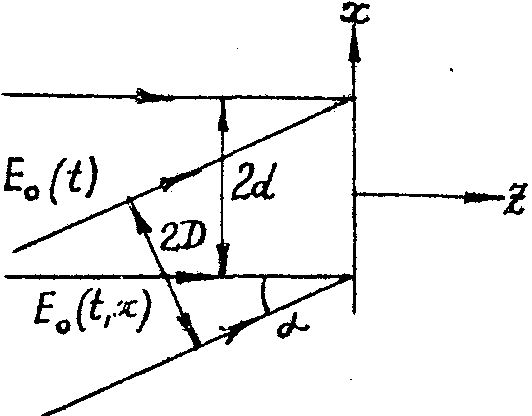
Рис.1. Схема записи голограммы нестационарного процесса.
(сигнал)
e0(t) = e
(t)exp[-iw
t]
направляется на фотопластинку перпендикулярно ее плоскости. Комплексная функция e
(t) характеризует нестационарность процесса, описывая изменение амплитуды и фазы сигнала во времени. Вспомогательное излучение (опорный пучок) подается под некоторым углом к плоскости пластинки, В отличие от обычной голографии опорный пучок не является монохроматическим, частота излучения в нем линейно меняется по сечению пучка. Опорный пучок требуемого характера в плоскости голограммы имеет вид:
ea(t,x) = e
a×
exp[-iw
t +i×
a×
x×
t×
cosa
+i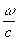 x×
sina
]
x×
sina
]
где
a характеризует скорость изменения частоты по сечению пучка. Существенно, чтобы полное изменение частота по сечению опорного пучка охватывало необходимый спектр частот исследуемого сигнала с тем, чтобы на голограмме были зарегистрированы все нужные
- 113 -
спектральные компоненты исследуемого излучения с их амплитудами и фазами, полное изменение частоты
2ad, где 2d ширина пучка, определяет временное разрешение tразр~½ad
Совместное действие исследуемого сигнала
e0(t) и опорного пучка ea(t,x) дает на регистрирующем элементе интенсивность, которая в процессе регистрации будет просуммирована за полное время регистрации tполн. Можно принять, что время регистрации от -¥
до +¥
, т.к. экспонирование производится только во время действия сигнала.
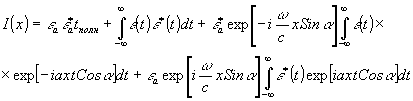
В результате экспонирования на пластинке образуется почернение, которое определяет прозрачность проявленной пластинки для поля. при отсутствии или при компенсации дополнительных фазовых искажений, даваемых пластинкой, будем иметь
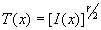 . Если принять, как это обычно делается в голографии, что амплитуда поля опорного пучка значительно больше амплитуды сигнала e
a
. Если принять, как это обычно делается в голографии, что амплитуда поля опорного пучка значительно больше амплитуды сигнала e
a>>
|
e
(t)
|
, то для амплитудной прозрачности пластинки можно воспользоваться.
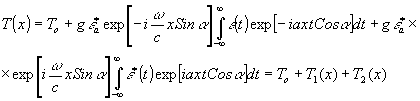
То описывает несущественную в данном случае постоянную прозрачность,
g - постоянный коэффициент, зависящий от коэффициента контрастности, Т1(x)
и Т2(x)
введены для сокращения записи. Таким образом, амплитудное пропускание фотопластинки содержит информацию о Фурье-образе исследуемого сигнала
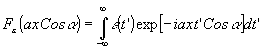
- 114 -
Подчеркнем, что в отличие от обычных схем голографии здесь регистрируются временные, а не пространственные Фурье-компоненты.
2.
Воспроизведение сигнала
Рассмотрим метод извлечения информации о временной картине сигнала /8/. В этом случае при воспроизведении сигнала выполняется обратное преобразование Фурье. На фотопластинку направляется восстанавливающий световой пучок
eb(t,x) = e
b×
exp[-iw
t +i×
b×
x×
t×
cosa
+i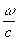 x×
sina
]
x×
sina
]
который формируется по такому же принципу, что и опорный, но, возможно, при другой скорости
b изменения частоты по сечению пучка. Кроме того, принято, что восстанавливающий пучок падает на голограмму под углом a
, так же как и опорный. Структура восстановленного поля на выходе на расстоянии r
от голограммы определяется формулой Кирхгофа, справедливой для немонохроматических полей /9/
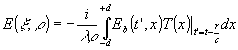
для составляющей поля, обусловленной прозрачностью голограммы, описываемой
Т1(x)
, имеем
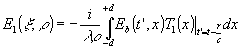
Ограничимся приближением Френеля, для точки наблюдения с координатами x
,r
имеем 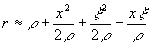 . В этом случае
. В этом случае
exp[-i×
b×
x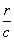 cosa
] »
exp[-i×
b×
x
cosa
] »
exp[-i×
b×
x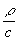 cosa
]
cosa
]
Вклад членов, пропорциональных
exp[i×
x2], будет несуществен при наблюдении в дальней зоне, когда r
>>x, или при использовании линзы, помещенной вблизи плоскости голограммы. Соответствующий выбор линзы позволяет скомпенсировать фазовые сдвиги 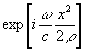 при условии ¦
=r
.
при условии ¦
=r
.
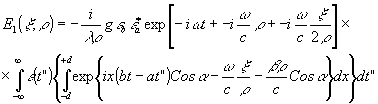
- 115 -
Вычисление интеграла по
x дает
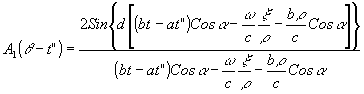
Для
e1(x
,r
) получаем свертку сигнала e
(t") с аппаратной функцией a1(q
-t"), определяющей временное разрешение системы. Оценка разрешения дает
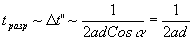
Это разрешение обусловлено конечным диапазоном зарегистрированных при записи голограммы частот исследуемого сигнала. Ограничиваясь таким временным разрешением, получаем
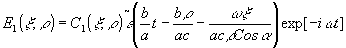 -
-
- сигнал, амплитуда которого меняется с временным масштабом
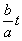 . Слагаемое
. Слагаемое 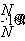 - временная задержка при распространении сигнала на расстояние r
. Слагаемое
- временная задержка при распространении сигнала на расстояние r
. Слагаемое 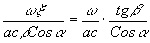 описывает угловое распределение сигнала.
описывает угловое распределение сигнала.
Схематическое изображение картины восстановленного сигнала
для начального момента этапа восстановления дано на рис.2, момент времени t=0 соответствует координате 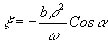 или
или 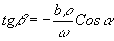 . Увеличение времени соответствует росту координаты x
или угла b
в отрицательную область, в процессе этапа восстановления полученная картина поворачивается в сторону положительных углов b
.
. Увеличение времени соответствует росту координаты x
или угла b
в отрицательную область, в процессе этапа восстановления полученная картина поворачивается в сторону положительных углов b
.
Следует отметить, что возможно восстановление сигнала стационарным световым пучком
(b=0). В этом случае имеем
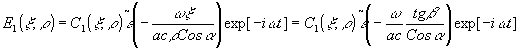
Время меняется в направлении отрицательных координат
e
или углов b
. Временная картина сигнала переводится в координатную с линейным
- 116 -
масштабом по координате.
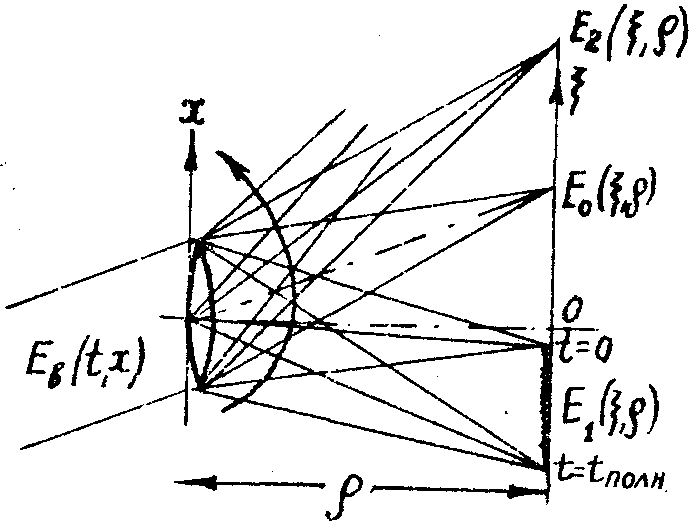
Рис.2. Схема восстановления временной картины сигнала для начального момента этапа восстановления в процессе восстановления картина поворачивается в направлении, указанном сплошной стрелкой.
Аналогичным образом рассмотрим составляющую поля, обусловленную прозрачностью голограммы, описываемой
t2(x).
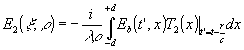
Ограничиваясь приближением Френеля и учитывая действие линзы с ¦
=r
, получаем
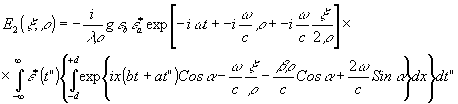
т.е. свертку сигнала
e
*(t") с аппаратной функцией А2(
q
-t")
. с учетом временного разрешения будем иметь
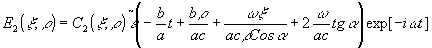
Для этой составлявшее характерно обратное течение времени при восстановлении.
Схематическое изображение картины приведено на рис.2 для
- 117 -
начального момента этапа восстановления. Момент времени
t=0 соответствует координате 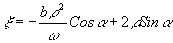 или
или 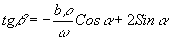 . Для малых углов a
этот угол приблизительно на 2a
отличается от угла, соответствующего полю e1(x
,r
). Увеличение времени соответствует росту координаты или угла в положительном направлении. В процессе этапа восстановления полученная картина поворачивается в сторону положительных углов.
. Для малых углов a
этот угол приблизительно на 2a
отличается от угла, соответствующего полю e1(x
,r
). Увеличение времени соответствует росту координаты или угла в положительном направлении. В процессе этапа восстановления полученная картина поворачивается в сторону положительных углов.
При восстановлении в статическом случае
(b=0) получаем
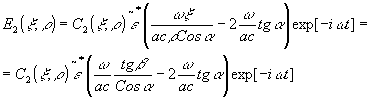
Время меняется в направлении положительных координат или углов b
. Временная картина сигнала переводится в координатную с линейным масштабом.
Наконец, рассмотрим составляющую поля, обусловленную постоянной прозрачностью голограммы То
. В рамках сделанных приближения с учетом временного разрешения получаем
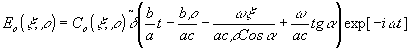
Для начального момента этапа восстановления схематическое изображение дано на рис.2. Момент времени
t=0 соответствует координате 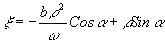 или
или 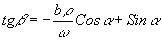 , т.е. соответствует приблизительно начальному направлению восстанавливающего пучка. В процессе этапа восстановления это направление поворачивается в сторону положительных углов b
. Для статического случая (b=0) имеем
, т.е. соответствует приблизительно начальному направлению восстанавливающего пучка. В процессе этапа восстановления это направление поворачивается в сторону положительных углов b
. Для статического случая (b=0) имеем
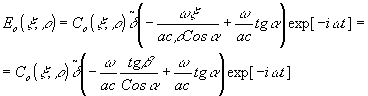
Таким образом, осуществляется восстановление временной картины сигнала с заданным временным масштабом
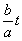 и с временным
и с временным
- 118 -
разрешением
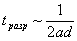 . Все составляющие восстановленного поля разделены в пространстве и не мешают на этапе реконструкции сигнала.
. Все составляющие восстановленного поля разделены в пространстве и не мешают на этапе реконструкции сигнала.
3.
Спектр сигнала
Запись голограммы содержит Фурье-образ исследуемого временного распределения, т.е. зарегистрированная величина содержит именно спектр сигнала. Однако, эта запись содержит и другие составляющие. Таким образом, задача состоит в преобразовании полученной картины с целью освобождения ее от мешающих составляющих.
При использовании стационарного восстанавливающего пучка, падающего на голограмму под углом a
, получим восстановленное поле вида
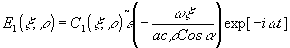
Имеем стационарное распределение поля по координате
x
. Другие составляющие поля могут бить убраны диафрагмой, поскольку имеет место пространственное разделение составляющих восстановленного сигнала. Для получения спектра сигнала можно использовать линзу, расположенную на расстоянии r
от голограммы /10/. Эта линза дает фазовый сдвиг 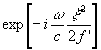 . Поле на расстоянии r
' от линзы будет
. Поле на расстоянии r
' от линзы будет
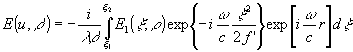
где
x
1 и x
2 границы области, в которой содержится полезный сигнал. Учитывая приближенна Френеля и принимая во внимание, что линза изображает голограмму в плоскости наблюдения 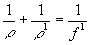 , получаем
, получаем
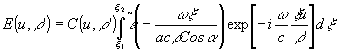
Ограничения накладываются апертурой пучка восстановленного сигнала
e1(x
,r
). Эта апертура ограничена в рассматриваемом случае диапазоном для t=0 и для t= tполн, т.е. имеем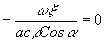 ,
, 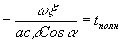 и x
o
и x
o=0,
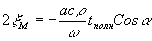 . Итак, в выражении для поля следует принять x
1
. Итак, в выражении для поля следует принять x
1=0
и 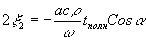 ;
;
- 119 -
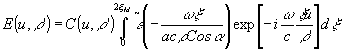
Перейдем к спектральному представлению исследуемого сигнала
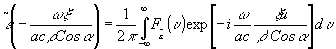
Меняем порядок интегрирования
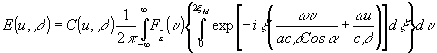
Для интеграла по Х получаем
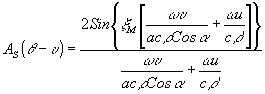
Таким образом, имеем свертку спектра сигнала с аппаратной функцией. Спектральное разрешение с учетом критерия Релея будет d
u
=2p
/tполн. Спектральное разрешение определяется полным временем регистрации сигнала. С учетом спектрального разрешения
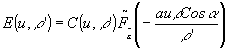
т.е. имеем спектр исследуемого сигнала. Мешающие компоненты исключены. Ограничение временного разрешения в данном случав дает зарегистрированный спектральный интервал или область дисперсии
D
u
= a×
d×
cosa
~ 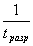
Схема получения спектрального состава зарегистрированного сигнала представлена на рис.
5.
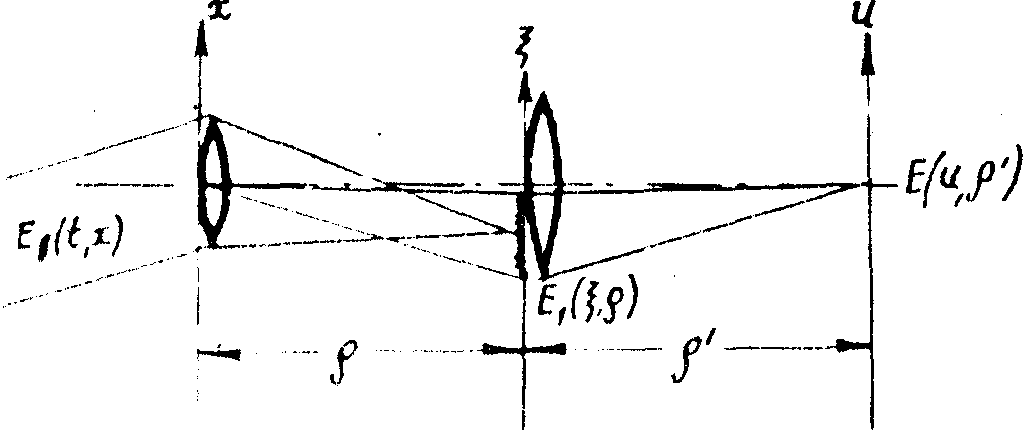
Рис.5. Схема получения спектра зарегистрированного сигнала.
- 120 -
4. Фаза сигнала.
Пусть исследуемой сигнал имеет вид:
e0(t) = e
(t)exp[-iw
t] = e(t)exp[ij
(t)]exp[-iw
t]
e(t)
и j
(t) действительные функции, описывающие изменение амплитуды и фазы во времени, задача заключается в ток, чтобы из зарегистрированного сигнала извлечь информацию о фазе j
(t). Решение этой задачи может быть выполнено по методу, аналогичному методу извлечения информации с фазах для статического фазового объекта /11/.
Интересующая нас прозрачность голограммы описывается выражением
t1(x) = ge
*a×
exp[-i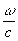 x×
sina
]f2(a×
x×
cosa
)
x×
sina
]f2(a×
x×
cosa
)
Для исследуемого сигнала следует выполнить операцию дифференцирования. Для этого достаточно поместить в плоскости голограммы транспарант с амплитудной прозрачностью
a×
x×
cosa
/a×
d×
cosa
, т.е. прозрачность его линейно меняется в рабочий области от 0 до 1. В статическом варианте восстановления (b=0) восстановленное поле на расстоянии r
от голограммы будет
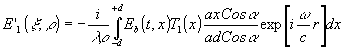
В приближении Френеля и при использовании линзы с
¦
=r
, помещенной рядом с голограммой и дающей фазовый сдвиг, 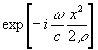
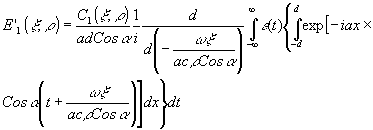
Интеграл по Х описывает аппаратную функцию
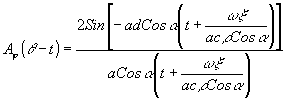
- 121 -
Окончательно получаем производную от свертки сигнала о аппаратной функцией
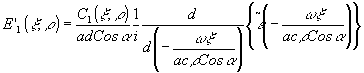
Для выделения информации о фазе сигнала в эту же плоскость направляется сигнал, восстановленный обычным образом в статическом варианте
e1(x
,r
) = c1(x
,r
)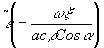
Один из вариантов реализации оптической схемы совмещения таких сигналов приведен на рис.4. Для разделения светового пучка на два
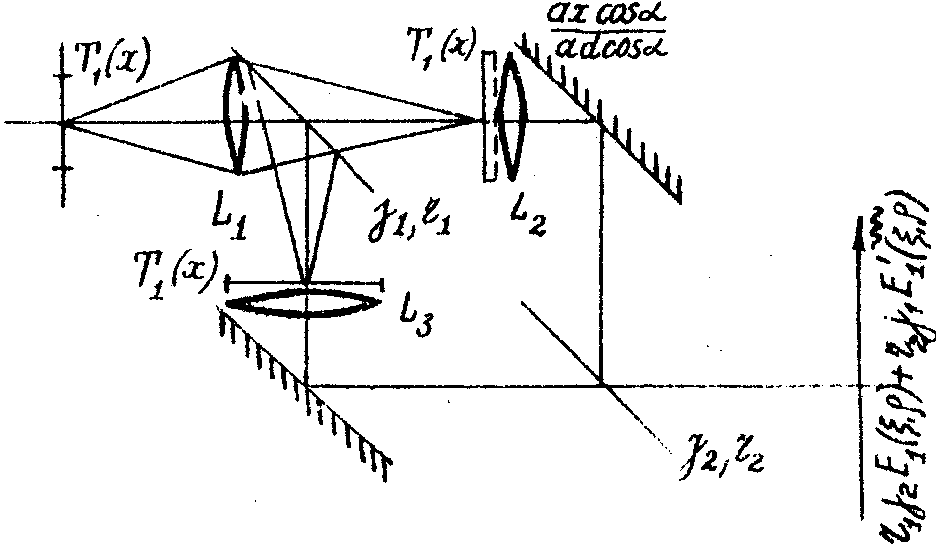
Рис.4.Схема получения информации о фазах зарегистрированного сигнала.
канала используется система с промежуточным изображением голограммы (линза
l1) и с двумя делительными пластинками, имеющими прозрачность для поля g
1 и g
2 и отражение r1 и r2. Таким образом, в плоскости наблюдения получается из первого канала поле g
1r
2e'
1(
x
,
r
)
и из второго канала поле g
2r
1e
1(
x
,
r
).
Линзы l2 и l3 используются для коррекции фаз. В плоскости x
,r
регистрируется интенсивность
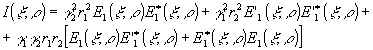
- 122 -
Делительные пластинки можно выбрать таким образом, что g
1r
2<<
g
2r
1. В этом случае вкладом члена 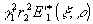 можно пренебречь. Подставим в полученное соотношение выражения для амплитуды исследуемого поля e
(t)=e(t)exp[ij
(t)] и
можно пренебречь. Подставим в полученное соотношение выражения для амплитуды исследуемого поля e
(t)=e(t)exp[ij
(t)] и 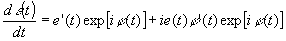 . Тогда
. Тогда
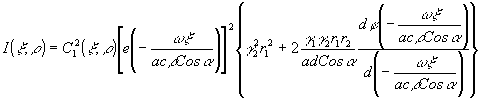
Для извлечения информации о фазе, т.е.
dj
(t)/d×
t, следует выполнить операцию деления. Транспарант, на котором зарегистрирована интенсивность i(x
,r
), при соответствующих условиях проявления и при устранении фазовых искажений, создаваемых эмульсией, будет обладать прозрачностью для поля, разной i(x
,r
). Для деления требуется транспарант, на которой зарегистрирована величина 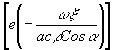 этот транспарант
этот транспарант
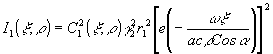
может быть изготовлен в той же оптической системе (рис.4) при использовании только второго канала.
После выполнения операции деления, на которой здесь останавливаться не будем (см., например, /10/), получаем требуемую информацию в виде производной фазы по времени или частоты в данный момент времени, наложенной на постоянный фон,
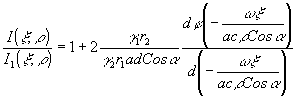
В случае необходимости может быть выполнена операция интегрирования для получения величины
j
(t) /10/.
Таким образом, на основании рассмотренного метода голографической
- 123 -
регистрации записывается полная информация об оптическом сигнале. Способы оптической обработки полученной информации позволяют извлечь временные и спектральные характеристики сигнала.
Литература
1.
А.Н.Зайдель. Г.В.Островская, Ю.И.Островский. Т.Я.Челидзе. ЖТФ. 36, 2208. 1966.
a.kakos, g.ostrovskaya, yu.0strovsky, a.zaidel. phys. lett., 23, 81, 1966.
2. И.П.Налимов. Применение голографии. Приложение 2 в книге Дж.Строук "Введение в когерентную оптику и голографию". Изд. "Мир", Москва, 1967.
3. f.m.mottier. appl.phys.lett., 15, 44, 1969.
h.j.saulfield. appl.phys.lett., 16, 234, 1970.
4. Ю.Н.Денисюк, Д.И.Стаселько. ДАН СССР, 176, 1274, 1967.
5. Ю.Н.Денисюк, Д.И.Стаселько, В.П.Минина. Опт.-мех. пром-ть, № 11. 73, 1968.
В.А.Косниковский, В.П.Минина, Д.И.Стаселько. "Голография и ее использование в оптике", часть i, Ленинградский дом научно-технической пропаганды, Л., стр. 34, 1970.
6. j.w.goodman. appl.opt., 6, 857, 1967.
7. В.А.Зубов, А.В.Крайский, Т.И.Кузнецова. Письма ЖЭТФ, 13, 443. 1971.
8. В.А.Зубов, А.В.Крайский, Т.И.Кузнецова. Авторское свидетельство №3
03618.
В.А.Зубов, А.В.Крайский, Т.И.Кузнецова. Аннотации докладов, представленных на 5-ую Всесоюзную конференцию по нелинейной оптике. Изд. Московского Университета, №15, стр.
155, 1970.
9.
А.Н.Тихонов, А.А.Самарский. Уравнения математической физики. Гос. изд-во техн.-теор.лит, Москва, 1953.
10. l.j.cutrona. e.n.leith, c.j.porcello. tre transactions on information, it-6, n 3, 386,. 1960.
(Перевод: Зарубежная радиоэлектроника, №
10, 3, 1962).
11.
Дж.Де Велис, Дж.Рейнольдс. Голография. Сокращенный перевод с английского. Воениздат, Москва, 1970.

