|
|
 |
 |

|
| |
СТАТИСТИЧЕСКАЯ ОПТИКА
В.А.Зверев
Преобразование изображений оптической системой может быть описано с помощью частотно-контрастных характеристик (ЧКХ). Форма ЧКХ оптической системы зависит как от параметров самой системы (характеристик объектива, геометрического расположения частей установки), так и от статистических параметров излучения, формирующего входное изображение. В данной работе выясняется зависимость вида ЧКХ оптической системы как от ее параметров, так и от статистических свойств источника излучения. Рассмотрены ЧКХ для двух моделей некогерентного освещения, в одной из которых задается распределение интенсивности света на входной плоскости, а в другой задается форма углового спектра мощности. Показано, что этих моделей преобразования изображений оптической системой может быть описано посредством операций, аналогичных линейной фильтрации, в которых совпадающие по форме ЧКХ получаются для различных настроек оптической системы и для различных сигналов. Проведено сравнение пространственной фильтрации изображений, осуществляемой оптической системой при когерентной и некогерентном освещении. Показано, что процесс пространственной фильтрации изображений при когерентном освещении описывается принципиально другой эквивалентной схемой. Приведены радиотехнические аналогии процессам фильтрации оптических изображений в когерентном и некогерентном свете и показаны отличия оптических фильтров от их радиотехнических аналогов.
- 95 -
1. Преобразование комплексных амплитуд поля оптической системой
Оптической системой мы называем среду, состоящую из двух участков свободного пространства, между которыми помещен оптический объектив.
С целью предельного упрощения и сокращения математических расчетов введем следующие идеализации. Поля будем считать квазимонохроматическими и зависящими только от одной пространственной координаты x и не будем учитывать эффектов, связанных с поляризацией волн. Эти упрощения не скажутся на общности полученных физических результатов. Зависимость полей от пространственной координаты x описывается с помощью комплексной функции p(x), модуль которой совпадает с амплитудой поля, а аргумент - с фазой волны /1/.
Если обозначить комплексную амплитуду на входе оптической системы через p(x), а на выходе через p(x), то связь между ними можно получить в следующем виде /2/:
 (1) (1)
где функция Г( x,x') зависит от параметров оптической системы.
Для того, чтобы написать выражение для функции Г( x,x') дадим математическое определение операции, совершаемой объективом оптической системы. Под объективом мы будем понимать модулятор поля, изменяющий амплитуду и фазу падающего на него излучения по закону l(x), где модуль комплексной функции l(x) определяет закон изменения амплитуды поля, а аргумент - закон изменения фазы. Функцию l(x) запишем в виде
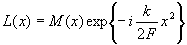 (2) (2)
Здесь f - фокусное расстояние объектива, 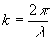 , l
- длина волны, М(x) - комплексный множитель. , l
- длина волны, М(x) - комплексный множитель.
На основании соотношения (2) дадим ряд определений. Оптическую систему, содержащую объектив, имеющий m(x)=1
- 96 -
для всех Х , назовем идеальной. Хотя физически такую идеальную оптическую систему невозможно реализовать, она играет большую роль в теоретических расчетах. Оптическая система с объективом, имеющим М(x)=1 на конечном участке изменения Х, вне которого модуль М(x) обращается в нуль, может быть физически реализована. Такую оптическую систему будем называть безаберрационной. Величину участка, где |
m(x)|
¹
0, назовем апертурой. В общем случае множитель m(х) учитывает отличия оптической системы от идеальной, вызванные как конечностью апертуры, так и наличием аберраций.
Для функции Г( x,x'), входящей в (1), можно получить следующее выражение:
 (3) (3)
где а - расстояние от плоскости, где задано поле p(x), до объектива; b - расстояние от объектива до плоскости, где определяется поле p(x).
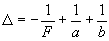 (4) (4)
D
- параметр оптической системы, который назовем настройкой оптической системы.
Интеграл, входящий в (3), легко вычисляется для идеальной оптической счетами, когда М(x)=1, а для реальных систем в следующих двух случаях, когда
D
= 0 (5)
и когда
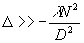 (6) (6)
где d - величина апертуры объектива, n - число степеней свободы
- 97 -
функции m(x), т.е. произведение ширины ее спектра на длительность. Для безаберрационной системы n=1.
В случае настройки оптической системы, определяемой (5), интеграл в (3) переходит в интеграл Фурье. Это случай реализуется при наблюдении поля в оптически сопряженной плоскости
При выполнении соотношения (6) выражение (1) может быть приближенно записано в виде
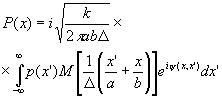 (7) (7)
где
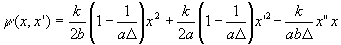 (8) (8)
2. Преобразование поля, обусловленное отклонениями параметров реальной оптической системы от идеальных.
Полученное выражение (7) Для преобразования полей является довольно сложным для использования в дальнейших расчетах. Преобразуем его к белее удобному виду. С этой целью введем вспомогательное преобразование поля, осуществляемое идеальной оптической системой с той же настройкой. Для идеальной оптической системы из соотношений (1) и (3) получаем
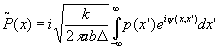 (9) (9)
где значение y
(x,x') определяется соотношением (8)
Из соотношения (9) можно найти функцию p(x) и результат подставить в (7). Проделав эту операцию, получаем связь между преобразованиями полей в идеальной и реальной оптических системах в виде
- 98 -
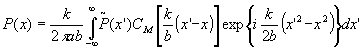 (10) (10)
Здесь функция cm(u) является спектром функции М(x), определяемой соотношением
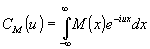 (11) (11)
Для оптической системы, имеющей достаточно большую апертуру при некотором ограничении рассматриваемого участка Х , когда справедливо условие
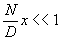 (12) (12)
экспоненциальный множитель под знаком интеграла в (10) можно опустить, после чего (10) приобретает следующий простой вид;
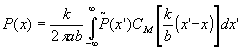 (13) (13)
Соотношению (13) можно дать следующее толкование. Преобразование сигнала оптической системой можно представить в виде двух операций, совершаемых последовательно. Сначала совершается операция (9) преобразования сигнала идеальной оптической системой. Это преобразование отражает, в основном зависимость формы сигнала на выходе от настройки оптической системы.
Следующая операция, выражаемая соотношением (13), представляет собой линейную фильтрацию выхода идеальной оптической системы. Она описывает те искажения, которые возникают из-за отличия реальной системы от идеальной.
Из соотношения (13) следует, что частотной характеристикой эквивалентного фильтра является функция М(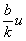 ). Здесь u - пространственная частота, а функция М(x) характеризует аберрации объектива оптической системы. ). Здесь u - пространственная частота, а функция М(x) характеризует аберрации объектива оптической системы.
Такое представление выхода оптической системы в виде
- 99 -
последовательности двух операций удобно для решения тех статистических задач, о которых пойдет речь ниже.
Выражений (10) сохраняет свой вид и при настройке оптической системы, удовлетворяющей соотношению (5).
Оптические приборы реагируют на среднюю интенсивность света, которая, согласно определение, равна среднему от квадрата модуля комплексной амплитуды. Зависимость среднего квадрата модуля от координаты Х, наблюдаемую в выходной плоскости, т.е. на расстоянии b от объектива, назовем изображением.
Используя соотношение (10) для изображения на выхода оптической системы, получим
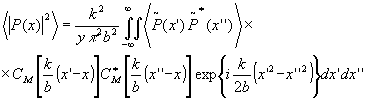 (14) (14)
Из соотношения (14) следует весьма важный вывод. Для того, чтобы вычислить изображение, необходимо знать корреляционную функцию комплексных амплитуд на выходе идеальной оптической системы Вид корреляционной функции, входящей в (14), зависит от настройки оптической системы и от статистических свойств источника света. Благодаря этому изображение на выхода оптической системы будет зависеть не только от настройки оптической системы, но и от статистических свойств источника излучения. Рассмотрим некоторые характерные случаи задания статистических параметров излучения.
2. Различные виды входных корреляционных функций
Задание пространственной корреляционной функции волнового поля на некоторой плоскости определяет как распределение энергии излучения по самой плоскости где задана функции, так и распределение энергии излучения по углам. Распределение энергии излучения вдоль плоскости и угловое ее распределение по углам могут варьироваться независимо, т.е. всегда найдется подходящая форма корреляционной
- 100-
функции, которая опишет излучение с требуемыми характеристиками вдоль плоскости и по углам. Для нас будут представлять интерес два крайних случая:
а) энергия излучения равномерно распределена по углам, а на плоскости представляет собой некоторую заданную функций координаты;
б) энергия излучения равномерно распределена по плоскости, а распределение по углам представляет собой заданную функцию угла наблюдения .
Путем суммировании корреляционных функций, соответствующих этим двум крайностям, можно получить общий случай.
Случай (а) реализуется, когда имеется самосветящийся экран с заданным распределением энергии излучения по экрану. Случай (б) реализуется при равномерном освещении поверхности параллельным световым пучком, неодинаково отражающей или рассеивающей свет под разными углами. В некоторых случаях сам "параллельный" пучок может описываться с помощью модели (б). Подберем для этих моделей описывающие их корреляционные функции.
Модель (а) описывается корреляционной функцией вида
<p(x’)p*(x")> = a2(x')d
(x'-x") (15)
где a2(x) - распределение интенсивности излучения по плоскости, d
(x) - d
-функция.
Для получения равномерного излучения по углам совсем необязательно, чтобы корреляционная функция (15) имела бы, как функция разности точек, вид d
-функции, вполне достаточно чтобы интервал корреляции был бы меньше или сравним с длиной волны. Во всех вычислениях корреляционная функция такой конечной ширины вела бы себя как d
-функция. На этом оснований она и фигурирует в формуле (15).
Модель (б) описывается корреляционной функцией вида
<p(x’)p*(x")> = В(x'-x") (16)
Вид функции В( x) определяется требуемым видом угловой зависимости
- 101- -
излучения. Распределение энергии излучения по углам или угловой спектр излучения определяется спектром Функции b(x) /3/.
Кроме этих двух, рассмотрим еще одну модель корреляционной функции, с помощью которой будем описывать когерентный свет. Если свет когерентен, то это означает, что функции p(x) становятся регулярными (по крайней мере, на рассматриваемом интервале значений координат и времени). При этом предположении получаем модель (в), описываемую корреляционной функцией вида
<p(x’)p*(x")> = p(x’)p*(x") (17)
4. Преобразование корреляционных функций идеальной оптической системой
Рассмотрим преобразование корреляционных функций идеальной оптической системой для двух случаев, когда наблюдение производится в оптически сопряженной плоскости и в фокальной плоскости.
В случае оптического сопряжения (D
=0) из формулы (9) следует, что распределения комплексных амплитуд во входной и выходной плоскостях находятся в однозначном соответствии. Из этого сразу следует, что если входная корреляционная функций содержит d
-функцию координат, то и выходная корреляционная функция будет также содержать d
-функцию координат.
Для модели (а) в этом случае получаем
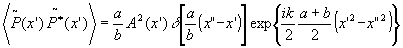 (18) (18)
В случае наблюдений в фокальной плоскости объектива, т.е. при b=f из формулы (9) следует, что распределение в выходной плоскости находится в однозначном соответствии со спектром входного сигнала. Для корреляционной функции на выходе идеальной оптической системы получаем соотношение:
- 102 -
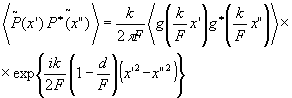 (19) (19)
где g(u) представляет собой Фурье-образ входной функции p(x).
5. Частотно-контрастная характеристика оптической системы для некогерентного света с заданным законом распределения интенсивности на плоскости
Рассмотрим теперь изображение на выходе оптической системы для модели (а), когда входная корреляционная функция описывается соотношением (15).
Пусть будет выполнено, кроме того, условие оптического сопряжения, когда корреляционная функция на выходе идеальной оптической системы дается соотношением (18). Подставляя (18) в (14), имеем:
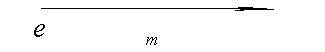 (20) (20)
Мы получили соотношение между распределениями интенсивности на входе и выходе оптической системы (реальной) при условии, что имеет место оптическое сопряжение.
Полученное соотношение по своей структуре, так же как и (13), напоминает преобразование сигналов линейным фильтром /4/. Импульсной переходной функцией в (20) является функция 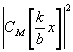 . Частотной характеристикой четырехполюсника будет, как известно /4/, ее спектр, т.е. функция вида . Частотной характеристикой четырехполюсника будет, как известно /4/, ее спектр, т.е. функция вида
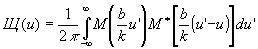 (21) (21)
Функция Щ (u) называется частотно-контрастной характеристикой
- 105 -
оптической системы, поскольку она определяет передачу пространственных частот в распределении интенсивности света /5/. Заметим, что функция Щ(u) является комплексной функцией, но такой, что справедливо - в силу (21) - соотношение
Щ *(u) = Щ(-u) (22)
при любом виде функции m(x).
Благодаря соотношению (22) на выходе фильтра обязательно будет действительный сигнал. В этом отношении частотно-контрастная характеристика аналогична комплексной частотной характеристике для электрических цепей /4/. Между ними имеется существенное различие /5/. Частотная характеристика для любой электрической цепи должна, кроме соотношения вида (22), обязательно удовлетворять так называемым условиям физической реализуемости, вытекающим из принципа причинности /4/. Частотно-контрастная характеристика аналогичным условиям удовлетворять не должна /5/.
Теперь изменим настройку оптической системы. Пусть теперь
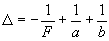 (23) (23)
Этот случай легко свести к уже рассмотренному посредством изменения вида функции М( x). Исходное выражение (10) справедливо при любой функции m(x). Поэтому выражение (2) мы можем записать в виде, формально всегда обеспечивающим условие оптического сопряжения:
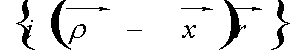 (24) (24)
Введем теперь новое 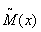
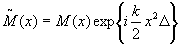 (25) (25)
Если подставить (25) в (24), то мы получим оптическую систему, всегда удовлетворяющую условиям оптического сопряжения, но с функцией 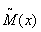 , определяемой (25). Появляется так называемая ошибка , определяемой (25). Появляется так называемая ошибка
- 104 -
фокусировки. Для частотно-контрастной характеристики остается справедливым выражение (21). Подставляя в (21) значение 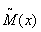 из (25), мы получим выражение для частотно-контрастной характеристики, справедливое для любой настройки оптической системы: из (25), мы получим выражение для частотно-контрастной характеристики, справедливое для любой настройки оптической системы:
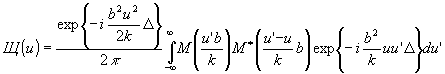 (26) (26)
которое можно также записать в виде
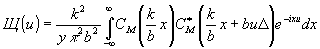 (27) (27)
Интересно отметить, что при достаточно больших D
, таких что
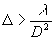 (28) (28)
ЧКХ, описываемые формулами (21) (для оптического сопряжения) и (26), ведут себя по-разному при увеличении апертуры d оптической системы. Ширина ЧКХ, описываемая формулой (21), для безаберрационного объектива апертуры d будет
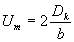 (29) (29)
так как в силу (21) она определяется взаимным перекрытием функции m(x).
В силу (27) ширина ЧКХ определяется перекрытием функций Сm(u) , т.е. спектров М(x), и будет следующим образом зависеть от апертуры:
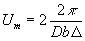 (30) (30)
Когда неравенство (28) превращается в равенство (29) и (30), результаты совпадают. При уменьшении D
следует пользоваться
- 105 -
соотношением (29), а при увеличении - соотношением (30). Как следует из (30), чем больше апертура, тем меньше становится ширина ЧКХ. Из условия (28) можно вывести требования к точности фокусировки оптической системы, при которой еще сохраняется ширина ЧКХ, определяемая соотношением (29).
Рассмотрим важный частный случай. Пусть мы ведем наблюдение изображения в фокальной плоскости объектива, т.е. когда D
=1/а . Из формулы (30) для ширины ЧКХ в этом случае мы получаем (учитывая, что b=f)
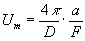 (31) (31)
Пусть а не превышает 2 f (случай большого d®
¥
мы не рассматриваем ввиду того, что при этом D
®
0, и мы должны пользоваться другой формулой для ширины ЧКХ). В этом случае для ширины ЧКХ мы получаем соотношение
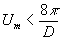 (32) (32)
При этом наименьший воспроизводимый пространственный период оказывается порядка величины апертуры d, т.е. идеальный безразмерный объектив работает при такой настройке как камера-обскурра с дыркой размером с апертуру объектива. Если апертура достаточно велика по сравнению с полем зрения, то можно сделать вывод, что информация о распределении интенсивности света вдоль входной плоскости почти не передается в фокальную плоскость.
6. Частотно-контрастная характеристика оптической системы для некогерентного света с заданными угловыми характеристиками рассеяния
Рассмотрение этого случая мы начнем с наблюдения в фокальной плоскости. Для корреляционной функции, входящей в выражение (10), в этой случае выполняется соотношение (19). В случав модели (б) (16) имеет место известное соотношение для корреляционных функций спектральных амплитуд:
- 106 -
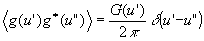 (33) (33)
где g(u) - угловой спектр мощности излучения.
Подставляя (33) в (19), а полученный результат в (10), имеем:
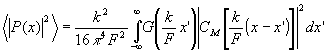 (34) (34)
Выражение (34) по своей структуре напоминает (20). Его также можно трактовать как отклик некоторого четырехполюсника, имеющего частотную характеристику вида (21). Изменился только входной сигнал. Теперь входным сигналом является распределение интенсивности излучения по углу. Изменилась и настройка оптической системы; теперь мы ведем наблюдение в фокальной плоскости объектива.
Изменение формы ЧКХ, которое будет при отклонении плоскости наблюдения от фокальной плоскости легко получить с помощью того же приема, который был продемонстрирован выше. Можно считать, что наблюдение происходит всегда в фокальной плоскости, а все изменения отнести за счет функций М( x).
В результате наблюдения в другой плоскости мы получим выражение для частотно-контрастной характеристики вида (26) и (27) и поэтому мы его не выписываем.
В частности, в случае модели (б) и наблюдении в оптически сопряжённой плоскости мы практически не получаем информации об угловом распределении излучения.
ли излучения практически можно разделить путем подходящего выбора настройки оптическое системы. При наблюдении в фокальной плоскости объектива мы можем получить необходимые параметры модели (б), а при наблюдение в оптически сопряженной плоскости можем получить параметры модели (а).
- 107 -
7. К вопросу об определении частотно-контрастной характеристики оптической системы для когерентного света
В случае когерентного света на вход оптическое системы подается регулярный сигнал, описываемый корреляционной функцией вида (17). Регулярным будет также и выход оптической системы, так как мы не учитываем флуктуации внутри самой системы. Следовательно, для корреляционной функции, входящей в (10), мы будем иметь
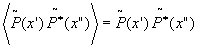 (35) (35)
Кроме того, будем считать выполненным условие (12), т.е. ограничим наблюдаемое поле зрения. В этом случав, принимая во внимание (13), получаем
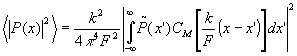 (36) (36)
Соотношение (36) справедливо при любой настройке оптической системы. Здесь частотная характеристика фильтра будет всегда 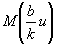 . Понятия частотно-контрастной характеристики сопоставимого с ЧКХ для некогерентного освещения, ввести нельзя. . Понятия частотно-контрастной характеристики сопоставимого с ЧКХ для некогерентного освещения, ввести нельзя.
8. Принципиальные отличия частотно-контрастных характеристик для некогерентного света от пространственной фильтрации сигналов при когерентном освещении
Полученное соотношение (36), описывающее изображение в когерентном свете, принципиально отличается от соотношений вида (20) и (34), полученных для различных моделей некогерентного освещения. Отличие здесь состоит не в форме самой ЧКХ, а лежит более глубоко, отличаются не параметры схемы, а сама блок-схема, описывавшая соответствующее преобразование. В случав некогерентного освещения фильтрации подвергается изображение, формируемое идеальной оптической
- 108 -
системой. При изменении настройки системы входной сигнал по своему виду не изменяется, а изменяются только характеристики фильтра.
В случае когерентного освещения фильтрация подвергается не изображение, формируемое идеальной оптической системой, а само поле, т.е. распределение комплексных амплитуд. При изменении настройки системы изменяется только входной сигнал, в то время как характеристики фильтра остаются практически неизменными (деформируются так же, как входные сигналы при некогерентном освещении).
Следующим отличием блок-схем является то обстоятельство, что результат фильтрации при некогерентном освещении непосредственно наблюдаем и не подвергается в дальнейшем при наблюдении никаким преобразованиям. При когерентном освещении результат фильтрации поля непосредственно не наблюдаем, а можно видеть лишь квадрат его модуля, т.е. только результат детектирования. Процессам пространственной фильтрации изображений в случае когерентного и некогерентного освещения можно сопоставить следующие радиотехнические аналоги. Случай, когда сигнал фильтруется фильтром, настроенным на высокую частоту, а мы наблюдаем результат детектирования выхода этого фильтра, аналогичен случаю когерентного освещения.
Фильтрация. сигнала на видеочастоте или звуковой частоте, когда мы наблюдаем или слышим результат фильтрации без дополнительного детектирования, соответствует схеме некогерентного освещения. Однако приведенная радиотехническая аналогия касается только самого построения блок-схемы и не идет достаточно далеко. Имеются принципиальные отличия в форме частотных характеристик фильтров.
ЧКХ любой оптической системы при некогерентном освещении определяются соотношением свертки вида (21), что приводит к сильным ограничениям на возможные формы ЧКХ. Соотношение вида (21) определяет положительно определенную функцию, одним из свойств которой является наличие абсолютного максимума в нуле. Таким образом, форма ЧКХ для некогерентного освещения всегда такова, что предпочтение отдается низким пространственным частотам. В этих условиях включение двух систем последовательно всегда приводит к сужению суммарной ЧКХ. Из этого следует, что в фотографии, снятой объективом с узкой ЧКХ, нельзя ничего исправить путем перефотографирования ее уже в условиях некогерентного освещения, применив
- 109 -
сколь угодно хороший объектив. Любой объектив в некогерентном свете способен только сузить суммарную ЧКХ. Этим свойством ЧКХ существенно отличается от радиотехнического фильтра видео или звуковых частот, а также от фильтров, осуществляющих фильтрацию полей в когерентном свете.
В когерентном свете фильтром для комплексной амплитуды является множитель m(x) (Этот множитель теперь не может быть произвольным. Для того, чтобы можно было изображение в когерентном свете представить в виде (36), должно быть выполнено условие (12). В это условие входит величина n - число степеней свободы функции М(x) в пределах апертуры d оптической системы. Чем меньше n, тем шире пространственная область применимости формулы (36). Поэтому в функцию М(x) для когерентного освещения нецелесообразно включать ошибку фокусировки, как это мы делали для некогерентного освещения). В когерентном свете можно производить фильтрацию полей не только в окрестности нулевой пространственной частоты, а и в области высоких частот путем простого сдвига функции m(x) вправо или влево от оптической оси объектива. В наблюдаемом сигнале мы вновь увидим низкие пространственные частоты, которые будут образовываться путем детектирования высоких пространственных частот. Подробно эти вопросы разобраны в радиотехнической литературе /6/.
Литература
1. Дж.Гудмен. Введение в Фурье оптику. Изд. "Мир", М., 1969.
2. М.Борн, Э.Вольф. Основы оптики. "Наука", 1970.
5. С.М.Рытов. Введение в статистическую радиофизику. "Наука", 1966.
4. Э.О'Нейл. Введение в статистическую оптику. Изд. "Мир", 1966.
5. И.С.Гоноровский. Радиотехнические цепи и сигналы. Часть i. Сигналы. Линейные системы с постоянными и переменными параметрами. Изд. "Советское радио", М., 1967.
6. И.С.Гоноровский. Радиотехнические цепи и сигналы. Часть ii. Нелинейные системы. Преобразование случайных процессов в линейных и нелинейных системах. Борьба с помехами. Изд. "Советское радио". М., 1967.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

