Основная идея регистрации поляризационных характеристик оптического излучения в голографии состоит в одновременной записи интерференционной картины, создаваемой в плоскости голограммы двумя ортогональными компонентами поля рассеянного объектом, и референтного поля. При этому должна быть предусмотрена возможность пространственной селекции картин, создаваемых рассеянием на голограмме каждой из поляризационных компонент в процессе восстановления. Нетрудно заметить что при этом должны выполняться два условия: 1) поляризационные компоненты референтной волны должны содержать различные пространственные частоты, т.е. практически создаваться разными источниками; 2) поляризация излучения этих источников должна быть такой, чтобы с помощью каждого опорного поля фиксировался только один поляризационный компонент объектной волны.

Для практического осуществления этой идеи в работе /1/ было предложено использовать две референтные волны с линейными ортогональными поляризациями, создающими излучение, описываемое в плоскости голограммы векторами /2/

где - единичный вектор направления поляризации соответствующей компоненты ; и - ее амплитуда и волновой вектор (начальные фазы каждой составляющей для простоты приняты равными нулю. j _i=0). Разложим проекцию поля , рассеянного объектом, на плоскость голограммы по компонентам Е⁽¹⁾ и .

Интенсивность суммарного поля в плоскости голограммы, очевидно, определяется выражением (см. рис.1):

Считая, что почернение фотопластинки определяется выражением Т=Т₀-k× i, получим уравнение векторной голограммы. При восстановлении теперь имеется возможность получить раздельную информацию о составляющих записанного на голограмме поля. Более того, если использовать два восстанавливающих источника с той же геометрией, что и при записи, волна будет иметь поляризацию, совпадающую с исходной.

1. Действительное x₁ - изображение:

где интегрирование проводится по плоскости голограммы. Это изображение формируется в направлении, определяемом множителем

2. Мнимое x₁ - изображение:

направление на которой определяется множителем

Знак минус в экспоненте, как обычно, показывает, что мнимое изображение создается расходящейся волной. Аналогичным образом записываются изображения, восстанавливаемые второй интерференционной решеткой, соответственно, в направлениях, определяемых множителями

Анализ полученных выражений показывает, что определенный выбор , и позволяет осуществить пространственную селекцию изображений, т.е. получить информацию об отдельных поляризационных компонентах рассеянной волны. При использовании двух восстанавливающих источников, расположенных в направлениях К₁ и с поляризациями, тождественными записывающим, непосредственно получаем полную картину поляризационной структуры поля.

проделывать с восстановленным изображением любые известные скалярные и векторные операции, что имеет большое значение, например, при изучении кратковременных процессов двойного лучепреломления. Использование подобного метода записи волны в оптической согласованной фильтрации позволяет осуществлять одновременную обработку сигналов по амплитудным, фазовым и поляризационным характеристикам объекта /5/. Однако, осуществление данных методов связано с целым рядом экспериментальных трудностей. Одна из них состоит в том, что правильное восстановление поляризации требует не только строгого сохранения амплитуд двух референтных пучков, но и соотношения фаз между ними. Действительно, записывая вектор Джонса, соответствующий полю, в виде

где , g =j ₀₂-j ₀₁, видим, что состояние поляризации зависит от отношения амплитуд компонент и их разности фаз. Ввиду этого практические схемы, выполненные по такой методике, предусматривают возможность обработки голограмм на месте экспонирования и компенсации усадки эмульсии фотопластинок /6/.

Подобный голографический метод выделений определенной поляризационной компоненты объектного луча нашел применение в фотоупругости /9/. В работах /10/ подробно описано получение голографических картин изоклинных, изохроматических и изопахических полос /11/. Путем добавления к стандартной голографической установке определенных поляризаторов был легко воспроизведен аналог требуемой поляризационно-оптической схемы. Например, для получения только изохроматических полос в опорный и объектный пуки вводились четвертьволновые пластинки, дающие круговую поляризацию. Однако надо отметить, что при строгом рассмотрении в выражение для интенсивности восстановленного с голограммы изображения изохром входит угол между интерферирующими пучками. Это приводит к понижению контраста полос и к их незначительному сдвигу /12/. Сдвига изохроматических полос можно избежать используя метод двух экспозиций. Для этого при одном и том же состоянии нагрузки модели на фотопластинку записываются две голограммы, причем в первой экспозиции используются одинаково линейно поляризованные опорная и объектная волны, во второй - поляризация пучков изменяется на ортогональную. В этом случае при восстановлении наблюдается только изменение контраста изохром. Об идентичности такого метода двух экспозиций с одноэкспозиционным, использующим циркулярно поляризованные волны, упоминается также в работе /13/. Однако, как будет показано ниже, это утверждение не совсем правильно и выполняется только при определенных условиях.

в голографий, т.е. превращения пространственной фазовой модуляции в пространственную модуляцию интенсивности /14/. Ввиду этого будем называть методом поляризационного контраста превращение изменений состояний поляризации по объекту в изменение интенсивности изображении, восстановленного с голограммы.

Теоретический анализ метода поляризационного контраста в голографии удобно проводить с помощью векторов Джонса e ₁ и e ₂ объектной и опорной волн /15/

Верхний индекс обозначает номер волны, нижний - соответствующую компоненту напряженности поля. Волна, рассеянная объектом, может быть представлена в виде следующего операторного равенства: e ₁=l× e _о, где e _о - вектор Джонса падающей волны; l - 2х2 матрица, описывающая преобразование объектом проекции напряженности электрического поля на плоскость голограммы.

где и i_b - амплитуда и интенсивность поля восстанавливающей волны, соответственно; j₁₂ и j₂₁ - матрицы взаимной корреляции, элементами которых являются корреляционные функции компонент объектной и опорной волн g_ij(x_kx_ℓ)=<e_k⁽ⁱ⁾e_ℓ^(j)*> i,j,k,ℓ=1,2.

Значок *) обозначает прямое Кронекеровское произведение матриц, а sp× a - сумму диагональных элементов оператора А. Угловые скобки обозначают усреднение по времени.

В случае, когда средние оптические пути объектного и опорного лучей выравниваются - интерферирующие поля полностью когерентны, тогда двувременные корреляционные функции, входящие в

(10), становятся одновременными. Ввиду чего усреднение по времени экспозиции позволяет упростить выражение (9),

Последнее соотношение совпадает с выражением, описывающим интенсивность волны, представленной матрицей когерентности j₁₁, прошедшей через анализатор, ориентированный вдоль направления вектора опорной волны /15/. Выражение (11) содержит полную информацию об объекте, поскольку в интенсивность мнимого изображения в явном виде входит оператор объекта l(i=l× j_00× l⁺), зависящий, в свою очередь, не только от амплитудных и фазовых, но и поляризационных характеристик объекта. Заметим, что для достаточно сложных объектов определение l из (11) связано со значительными трудностями математического характера. Однако эта задача может быть упрощена, если использовать в эксперименте различные состояния поляризации. Практический анализ объектов по этой методике сводится в конечной счете к вычислению проекций состояния поляризации объектной волны на состояния с линейными и циркулярными поляризациями. Поскольку оператор l содержит в общем случае 4 независимых элемента, ясно, что полное определение характеристик объекта требует выполнения четырех голографических экспериментов подобного типа. Однако во многих случаях число независимых переменных оператора l оказывается меньше четырех, так что необходимо знание только распределения определенного состояния поляризации по объекту. В качестве примера подобной ситуации рассмотрим объект, представляющий собой анизотропную фазовую пластинку с переменной толщиной, оператор l которой в собственной системе координат имеет вид;

где относительная фазовая задержка обыкновенного и необыкновенного лучей d (x,y) - произвольная функция координат. Подставляя (12) в (11) и используя для получения голограмм волны с произвольными состояниями поляризации, описываемые векторами Джонса

получим i_m = i_b¦ (r₀,r₂,v) = i_b[1+cos2(r₀+r₂)+

+sin2(r₀)× sin2r₂+sin2r_0× sin2r_2× cos(d (x,y)+g ₂-g ₀) (14)

где v=d (x,y)+g ₂-g ₀. Предполагая, что d (x,y) - малая величина, разложим функцию ¦ (r₀,r₂,v) в ряд вблизи значения v=v'=g ₂-g ₀ ограничиваясь двумя членами разложения, получим

Первый член представляет собой постоянный фон в изображении, а второй - переменную часть, которая несет информации об относительной фазовой задержи d (х,у). Для получения изображения с максимальным изменением интенсивности в соответствии с функцией необходимо выполнение соотношения

Нетрудно показать, что из (15) вытекают следующие условия:

Требования (16) накладывают ограничения на состояния поляризации опорной и падающей на объект волн. Условие для r предполагает такой выбор поляризации, для которых проекции вектора напряженности электрического поля на оси собственной системы координат кристалла равны между собой. Условие для g означает, что состояния поляризации волн должны быть различными, но вполне определенными. Например, волна, падающая на объект, циркулярно поляризована r₀=45^o, g _o=p /2. Тогда для получения максимального изменения интенсивности восстановленного изображения в соответствии с d (х,у) необходимо при записи голограммы использовать линейно

m_мдэ = i_b× sp(j₁₁j₂₂+j₃₃j₄₄+e^ij j₁₃j₄₂+e^-ij j₃₁j₂₄) (17)

где индексы 3, 4 соответствуют индексам 1, 2, но для второй экспозиции; множители exp[± ij ] возникают в результате относительного изменения оптических длин при первой и второй экспозиции. Первые два члена описывают изображение объекта при разных экспозициях, два последних - их интерференцию при восстановлении. Пусть далее объект задается оператором;

а референтная и освещающая объект волны линейны и ортогональны. Тогда из (17) следует

m_мдэ = i_b× [| ℓ_11| ²+| ℓ_22| ²+2re(ℓ₁₁ℓ^*₁₂e^ij )] (19)

m_М = i_b{| ℓ₁₁+ℓ_22| ²+| ℓ₁₂-ℓ_21| ²} (19)

Из сравнения (20) и (19) видно, что метод двух экспозиций эквивалентен одноэкспозиционному методу с циркулярной поляризацией полей только в случае выполнения следующего равенства:

2re[ℓ₁₁ℓ^*₂₂(1-e^ij )]+| ℓ₁₂-ℓ_21| ² (20)

Другими словами, оба метода дают одинаковые результаты лишь при определенных условиях (ℓ₁₂=ℓ₂₁ и j =0), накладываемых на поляризационные объекты и методику эксперимента. Класс таких объектов

довольно широк, поскольку в собственной системе координат оператор l имеет только диагональные элементы /16/. Однако, можно указать даже простейшие объекты, для которых ℓ_12¹ ℓ₂₁ /17/. Эксперимент должен проводиться без внесения фазовой задержки между экспозициями.

1 – he-ne лазер; 2 – пластинка; 3 - п.п. зеркало; 4 - 100% зеркало; 5 - поляризатор; 6 - микрообъектив; 7 - рассеиватель; 8 - объект; 9- голограмма; 10 - фотокамера.

ВР-Л. В качества объекта, хорошо иллюстрирующего приведенные выше соотношения 4, в то же время достаточно простого для получения количественных характеристик, был выбран клинообразный кристалл кварца, вырезанный параллельно оптической оси и описываемый оператором

d (x) = d (x₀)+(n_e+n₀)x× tgy (23)

x - текущая координата вдоль широкого катета сечения клина; d (х₀)=d (х)| _х=0=17p - начальная разность фаз между необыкновенной и обыкновенной волнами в точке х₀; y (1,5°) - угол клина; n_e, n₀ - показатели преломления кварца для необыкновенного и обыкновенного лучей. Волна e ₀ с произвольным состоянием поляризации /13/ после прохождения через данный объект принимает вид:

Выражение (24) определяет состояния поляризации волны, записываемой на фотопластинку. Необходимо отметить, что геометрическим местом точек на объекте, обладающих одинаковым видом поляризации, являются прямые линии, параллельные ребру клина. Для получения вполне определенной картины распределения поляризаций по объекту нами была выбрана волна e ₀ с линейной поляризацией под углом 45° к оси r₀=45°, g ₀=0. Тогда из выражений (23) и (24) следует, что для точек на выходной грани кристалла с координатами:

где i₁=0,1,2,3; ;l - длина волны. Объектная волна e ₁, соответственно, линейно поляризована под утлом 135° к оси Х (r₁=45^o, g ₁=0), циркулярно поляризована с левым вращением (r₁=45^o, g ₁=p ), линейно поляризована под углом 45° к оси x (r₁=45^o, g ₁=p ) циркулярно поляризована с правым вращением (r₁=45^o, g ₁=p ). Если для записи такой волны использовать опорный луч с произвольным состоянием поляризации e ₂, то интенсивность мнимого изображения восстановленного с голограммы, запишется, согласно /11/ в виде

i_m = 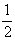i_b[1+sin2r_2× cos[d (x)+g ₂]] (26)

Были экспериментально получены голограммы данного объекта при различных поляризациях опорного пучка. Угол между интерферирующими лучами составлял 15°, так что изменением состояния поляризации опорной волны, возникающим при проектировании на плоскость

а) волна e ₂ линейно поляризована под углом 45° к оси Х (r₂=45^o, g ₂=0) (рис.3а); выражение (26) приникает вид;

i_m = 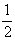i_b[1+cosd (x)] (27)

б) волна e ₂ циркулярно поляризована с правым вращением (r₂=45^o, g ₂=p /2) (рис.3б), тогда

i_m = 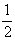i_b[1-sind (x)] (28)

в) волна e ₂ линейно поляризована под углом 135° к оси Х (r₂=45^o, g ₂=p ) (рис.3в):

i_m = 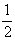i_b[1-cosd (x)] (29)

г) волна e ₂ циркулярно поляризована с левым вращением (r₂=45^o, g ₂=-p /2) (рис.3г):

i_m = 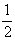i_b[1+sind (x)] (30)

Нетрудно показать, что выражения (26-29) описывают решетку интенсивностей с периодом Т_Х=2,7 мм, для которой i_mmin=0. Экспериментально положение полос решетки вычислялось относительно визира, установленного на выходной грани кристалла в точке с координатой » 5,4 мм. Как видно из фотографии, для случая (а) один из максимумов интенсивности восстановленного изображения совпадает с визиром, для случаев (б, в, г) максимумы смещены, соответственно, на , т.е. находятся в точках с координатами » 6,8 мм; » 7,4 мм. Аналогичным образом определялись положения i_mmin. Экспериментально вычисленные значения Х для максимумов и минимумов интенсивности совпадают со значениями, найденными из формуя (26-29). Анализируя подученные результаты и сравнивая их с (25), нетрудно заметить, что положение полос решетки зависит от состояния поляризации опорного пучка и от распределения поляризации по объекту. Другими словами, состояние поляризации опорного луча является

а) волна e ₂ линейно поляризована под углом 45^о;

б) волна e ₂ циркулярно поляризована с правым вращением;

в) волна e ₂ линейно поляризована под углом 135^о к оси;

г) волна e ₂ циркулярно поляризована с левых вращением.

Рассмотрим случай, когда в опорном и освещающем объем пучках используются круговые поляризации с одинаковым вращением. Например, r₀=r₂=45^o, g ₀=g ₂=p /2 (рис.4а). Подставляя эти значения в (11) и учитывая (22), получаем выражение, полностью совпадающее с выражением для интенсивности мнимого изображения, когда волны e ₀ и e ₂ линейно поляризованы под углом 45° (27). Сравним полученный результат с методом двойной экспозиции для того же объекта. Используя соотношение /19/, имеем

i_мдэ = 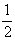i_b[1+cosd (x)+¦ ] (31)

Оператор l из (22) удовлетворяет равенство (21), поэтому при данных условиях картины, описываемые (27) и (31), совпадают. На рис.4б приведено мнимое изображение объекта, полученное по методу

двойной экспозиции при ¦ ¹ 0. Фазовая задержка вводилась клинообразностью поляризатора и образовывала периодическую решетку на диффузном рассеивателе. В результате на объекте наблюдается смешение полос и изменение периода решетки. Последнее следует из выражения (31) при подстановке и , где q _x - период решетки, образованной поляризатором, ¦ - постоянная фазовая задержка.

Рис.4. а - восстановленное мнимое изображение объекта, когда при записи голограммы используются круговые поляризации с одинаковым вращением;

б - восстановленное мнимое изображение объекта, полученное по методу двойной экспозиции при j ¹ 0.

2. А.А.Коростелев, А.С.Касаткин. Вопросы радиоэлектроники, сер. общетехническая, 22, 84, 1969.

5. А.А.Коростелев, А.С.Касаткин. Вопросы радиоэлектроники, сер. общетехническая, 23, 26, 1969.

9. hovanessian, brcic, powell. exper. mechanics, 8, 362, 1968. А.Н.Зайдель, В.С.Листовец и Ю.И.Островский, ЖТФ, 39, 12, 2225, 1969.

10. Г.Л.Хесин, В.Н.Сахаров, И.В.Жаворонок. Энергетическое строительство, 7, 50, 1969.

Г.Л.Хесин, В.Н.Сахаров, И.В.Жаворонок. Моделирование задач динамики термоупругости и статики поляризационно-оптическим методом, сб. трудов, №73, М., 118, 1970.

11. А.Дюрелли, У.Райли. Введение в фотомеханику. Изд. "Мир", М., 1970.

14. Л.М.Сороко. Основы голографии и когерентной оптики. Изд. "Наука", М., 1971.

15. И.А.Дерюгин, В.Н.Курашов, Д.В.Поданчук, Ю.В.Хорошков, УФН, 108, 4, 1972.

16. В.Я.Молчанов, Г.В.Скроцкий. Квантовая электроника. Сб. статей, изд. "Советское радио", М., 4, 3, 1971.

17. У.Шерклифф. Поляризованный свет. Изд. "Мир", М., 1965.