|
|
 |
 |

|
| |
нелинейные эффекты в голографии
Г.В.Островская
В работе рассмотрено влияние нелинейности зависимости амплитудного пропускания голограммы от экспозиции на восстанавливаемые голограммой волновые фронты. Исследованы вызванные нелинейностью записи искажения изображений 1-го порядка и вид изображений высших порядков. Рассмотрено влияние нелинейности на дифракционную эффективность голограмм. Обсуждаются возможности использования нелинейных эффектов для повышения чувствительности голографической интерферометрии, для получении дисперсионных голограмм, для пространственной фильтрации и некоторые другие применения нелинейных эффектов. В работе рассмотрены также эффекты, к которым приводит учёт нелинейности зависимости пропускания голограммы от экспозиции. Будет показано, как нелинейность сказывается на восстановленных голограммой волновых фронтах и изображениях, в каких случаях нелинейные эффекты несущественны и когда их следует учитывать. Во второй части работы рассмотрены некоторые возможные применения нелинейных эффектов.
Линейная регистрация голограммы. Прежде чей рассматривать нелинейные эффекты, напомним кратко, что понимается под линейной записью в голографии. Пусть на поверхность фотопластинки (рис.1а) (или любой другой светочувствительной среды) падают две волны: предметная u=a(x,y)exp[ij
(x,y)] и опорная u0=a0exp[ij
0]. Здесь x,y - координаты в плоскости голограммы, А и А0 - амплитуды и j
и j
0 - фазы волн. Амплитуду опорной волны будем считать постоянной, а фазу j
0 положим равной нулю, что соответствует плоской опорной волне, нормальной к поверхности голограммы. Тогда распределение
- 52 -
освещенности в плоскости голограммы примет вид:
e = |
u+u0|
2 = a02+a2+a0a[eij
+e-ij
] = a02+a2+2a0a×
cosj
(1)
Предположим, что амплитудное пропускание фотопластинки является линейной функцией экспозиции
t(x,y) = t0+t1×
h(x,y) (2)
Здесь экспозиция h=e×
t, t – время экспозиции. Подставляя в (2) значение Е из (1) получим
t = t0+t1(a02+a2)t+t1×
a0a×
t[eij
+e-ij
] (3)
Если мы теперь осветим эту пластинку (голограмму) волной, которая являлась опорной при записи голограммы (рис.1б), то на выходе из голограммы получим
v= t×
a0 = [t0+t1(a02+a2)t]a0+t1×
a02t×
a×
eij
+t1×
a02t×
a×
e-ij
=
= [t0+t1(a02+a2)t]u0+a02t×
t1u+a02×
t1×
u* (4)
первый член в правой части этого равенства соответствует волне нулевого порядка, распространяющейся в том же направлении, что и пучок, освещающий голограмму в процессе восстановления. Второй член только постоянным множителем a02t×
t1 отличается от предметной волны и представляет восстановленную волну 1-го порядка, дающую мнимое изображение предмета в том месте, где он находился
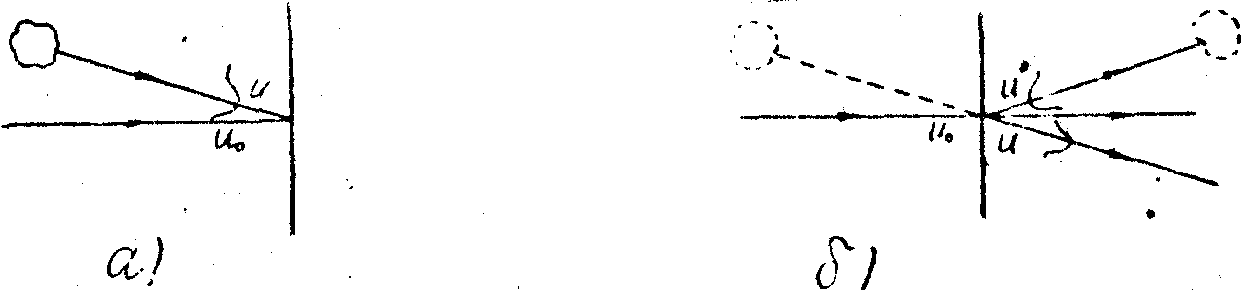
Рис.1. Схема получения голограммы (а) и восстановления волнового фронта (б).
- 53 -
при получении голограммы. Третий член соответствует волне 1-го порядка и дает сопряженное (действительное) изображение предмета.
Итак, при линейной записи голограмма позволяет восстановить волну, являющуюся копией записанной предметной волны., что является достаточным условием для получения изображения предмета, вне зависимости от использовавшейся схемы голографирования.
Реальная фотопластинка. Пропускание реальной фотопластинки связано с экспозицией зависимостью, существенно отличающейся от даваемой соотношением (2). Прежде всего, пропускание является комплексной функцией экспозиции
t(h) = t
(h)eiq
(h) (5)
Наличие фазового множителя связано с тем, что толщина и показатель преломления проявленной эмульсии зависят от ее почернения. Именно этим множителем обусловлены нелинейные эффекты, наблюдаемые для фазовых (отбеленных) голограмм /1/.
Амплитудное пропускание является, вообще говоря, нелинейной функцией освещенности. В фотографической фотометрии принято характеризовать фотопластинку с помощью характеристической кривой (рис.2а) – зависимости оптической плотности s (или почернения)
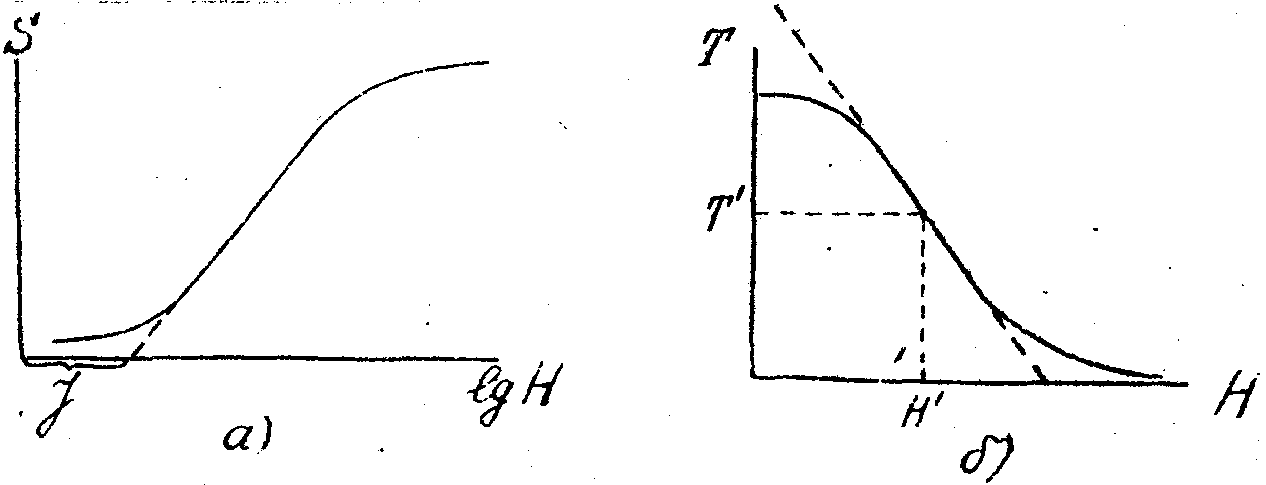
Рис.2. Характеристическая кривая фотопластинки (а) и зависимость амплитудного пропускания от экспозиции (б).
- 54 –
от логарифма экспозиции Н. Для линейного участка характеристической кривой имеем
s = j+g
×
ℓgh (6)
Где j – инерция пластинки и g
- ее контрастность. Оптическая плотность пластинки связана с ее амплитудным пропусканием соотношением s=ℓg(1/t2), откуда
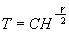 (7) (7)
Здесь С – постоянная связанная с j соотношением j=-2ℓgc. Из (7) видно, что запись является линейной для g
=-2. Отрицательное значение g
соответствует позитивной записи голограммы.
Обычно голограмму записывают на негативном фотоматериале, зависимость амплитудного пропускания которого от экспозиции дается кривой, изображенной на рис.2б. Некоторый участок этой кривой вблизи точки (h'1t') можно аппроксимировать прямой вида (2), однако коэффициент Т1 в этом случае отрицателен, что приводит к изменению фазы восстановленной волны на p
.
Если А<<А0, т.е. опорная волна намного интенсивней предметной, то локальная освещенность пластинки мало отличается от среднего значения, близкого к А02, и выбором соответствующего времени экспозиции всегда можно обеспечить условие линейной записи голограммы. При этом следует заметить, что линейный участок кривой Т-Н не совпадает с линейным участком (областью нормальных почернений) характеристической кривой, а соответствует области недодержек.
Условие А<<А0 приводит к низкому контрасту интерференционной структуры на голограмме и, соответственно, низкой ее дифракционной эффективности. Контраст интерференционной структуры дается соотношением:
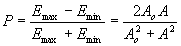 (8) (8)
Контраст и дифракционная эффективность голограммы максимальны при равенстве амплитуд предметной и опорной волн. Однако в этом
- 55 -
случае локальные изменения экспозиции не могут не выйти за пределы линейного участка кривой Т-Н.
Нелинейная запись голограммы. Как видно из формулы (1), освещенность голограммы является периодической функцией j
. Поскольку фаза предметной волны обычно меняется вдоль голограммы значительно быстрее, чем ее амплитуда, то освещенность, а следовательно, и экспозиция в плоскости голограммы меняются по косинусоидальному закону. При линейной записи пропускание голограммы также является косинусоидальной функцией координат. При выходе за линейную область кривой Т-Н пропускание голограммы остается периодической функцией j
, но вид этой функции может существенно отличаться от косинусоиды (см.рис.3). Эту периодическую функцию можно разложить в ряд Фурье по косинусам j
.
t = 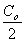 +c1cosj
+c2cos2j
+c3cos3j
+... = +c1cosj
+c2cos2j
+c3cos3j
+... =
= t
o+t
1(eij
+e-ij
)+t
2(e2ij
+e-2ij
)+t
3(e3ij
+e-3ij
) (9)
где коэффициенты Фурье С 0, С1, С2 и т.д. даются формулой
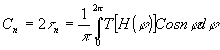 (10) (10)
В процессе восстановления световых волн с помощью голограмм, пропуская через нее плоскую монохроматическую волну, мы осуществляем Фурье-анализ ее пространственной структуры. При этом образуются дифрагированные волны не только 1-го, но и высших порядков. Углы, под которыми они распространяются, соответствуют гармоникам основной частоты пространственной структура голограммы, а их интенсивность пропорциональна коэффициентам t
n.
Для того, чтобы проанализировать влияние нелинейности регистрирующей среды на восстановленные голограммой волны, нужно представить зависимость пропускания от экспозиции в аналитическом виде. В литературе используются различные аппроксимации зависимости Т от Н . Так, в работе Козма /6/ функция t(Н) аппроксимируется интегралом вероятности. Фризем и Зеленка /7/ и Найт /8/ пользуются
- 56 -
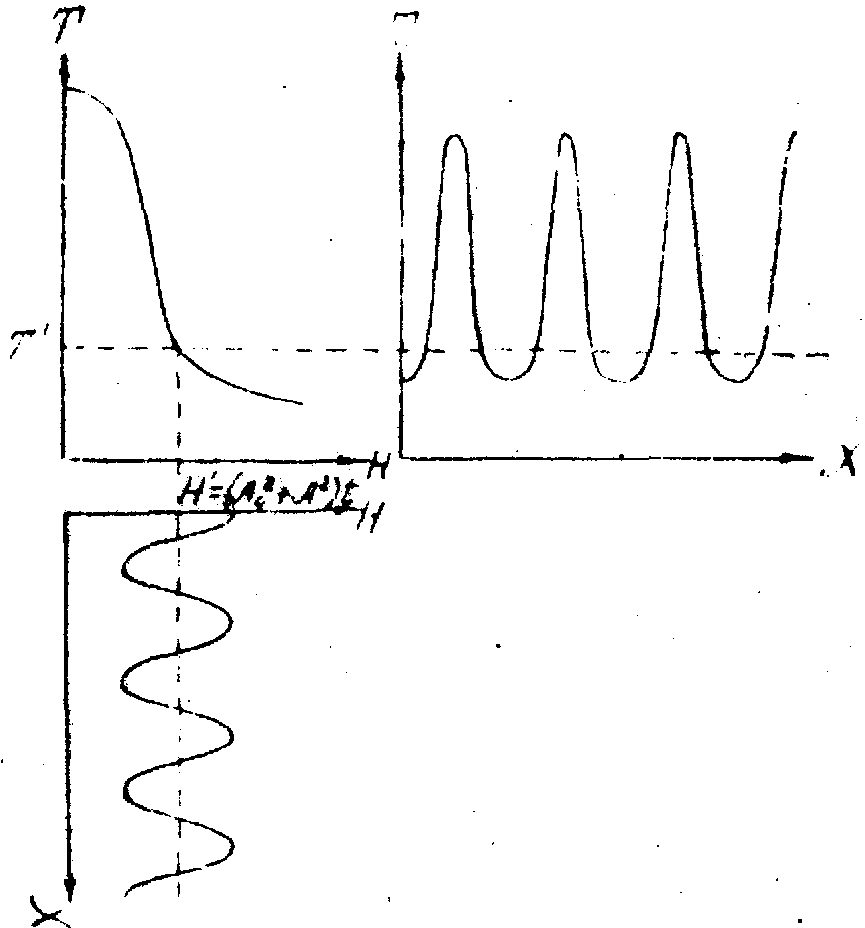
Рис.3. Искажение синусоидального распределения экспозиции из-за нелинейности кривой t=t(h).
зависимостью вида Т=к×
Нg
, Токарский /5/ и Денисюк и др. /9/ используют разложение Т(Н) в степенной ряд (по степеням 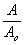 ), Упатникс и Леонард /10/ используют аппроксимацию вида t =exp[-k×
h2], а Вельцель /11/ представляет Т как exp[-k×
h], и, наконец, в работах /12-14/ используется модель резко контрастной пленки, для которой Т=Т0 при h<hпред. и Т=0 при h>hпред.. Здесь мы, следуя Гудмену и Найту /13/, Брингдалу и Ломану /15/ и Колье и др. /16/ воспользуемся разложением Т(Н) в ряд по степеням Н, причем, ограничимся членами со степенями Н меньше 3: ), Упатникс и Леонард /10/ используют аппроксимацию вида t =exp[-k×
h2], а Вельцель /11/ представляет Т как exp[-k×
h], и, наконец, в работах /12-14/ используется модель резко контрастной пленки, для которой Т=Т0 при h<hпред. и Т=0 при h>hпред.. Здесь мы, следуя Гудмену и Найту /13/, Брингдалу и Ломану /15/ и Колье и др. /16/ воспользуемся разложением Т(Н) в ряд по степеням Н, причем, ограничимся членами со степенями Н меньше 3:
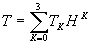 (11) (11)
Такая аппроксимация достаточно хорошо описывает, например, кривую Т(Н) для пластинок kodak 649 f (см./13,16/). Следует заметить, что вид нелинейной функции, используемой для описания зависимости Т от Н, приводит к изменению коэффициентов t
n в(10). Таким образом, от вида аппроксимации существенным образом зависит
- 57-
количественный вклад нелинейных членов в восстановленное изображение. Однако качественное объяснение большей части нелинейных эффектов может быть проведено с равным успехом при очень разных видах нелинейной зависимости t(h).
Подставляя в (11) вместо Н величину et, где Е дается формулой (1), после выполнения соответствующих алгебраических действий, получим
t = t
o+t
1(eij
+e-ij
)+t
2(e2ij
+e-2ij
)+t
3(e3ij
+e-3ij
) (12)
Здесь
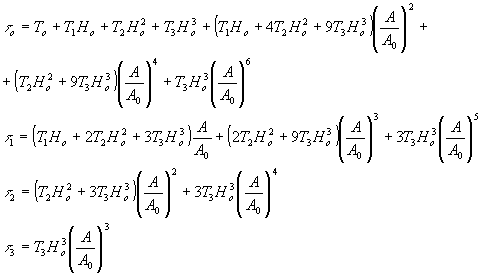 (13) (13)
где h0=a02t - экспозиция, создаваемая на голограмме одним опорным пучком.
Если в процессе восстановления используется плоская волна единичной амплитуда, падающая нормально к поверхности голограммы, то величина Т , даваемая выражением (12) представляет собой также и комплексную амплитуду восстановленной световой волны в плоскости голограммы. Член t
0 соответствует войне нулевого порядка, а члены с коэффициентами t
1, t
2 и t
3 ±
1-му, ±
2-му и ±
3-му порядкам дифракции, соответственно (рис.4).
Как видно из (12), фазы восстановленных волн в n раз больше, чем в первом порядке (n - порядок дифракции). Коэффициенты t
1, t
2 и t
3 в (12), соответствующие амплитудам восстановленных волн разных порядков, являются функциями экспозиции Н0,
- 58 -
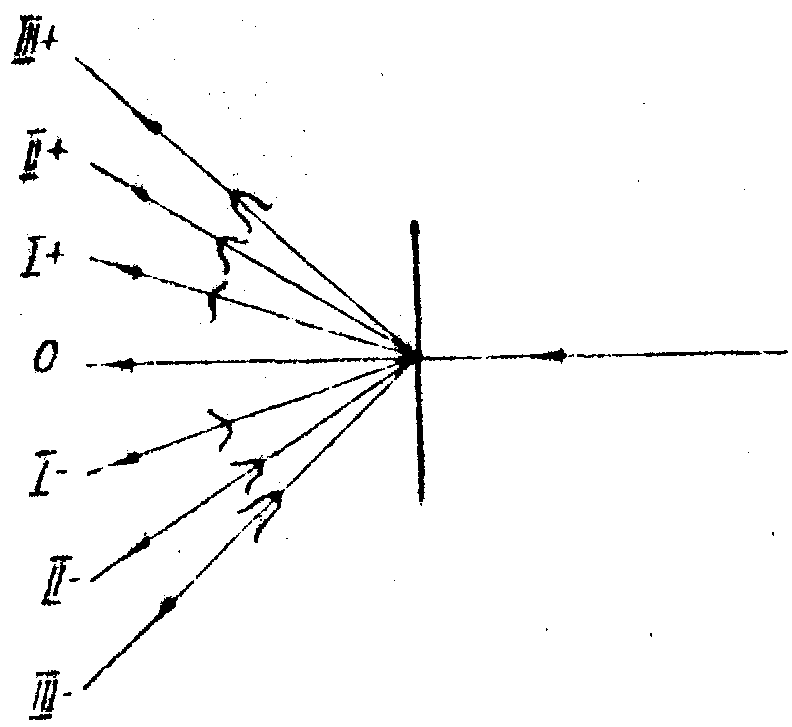
Рис.4. Восстановление волновых Фронтов с помощью нелинейной голограммы.
создаваемой опорным пучком, отношения амплитуд 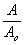 и величин Т0 и величин Т0, Т1, Т2 и Т3, характеризующих нелинейность фотоматериала. В результате этого амплитуды дифрагировавших волн не только высших, но и первых порядков не пропорциональны амплитуде, записанной на голограмме предметной волны. Только первое слагаемое в t
1 равное 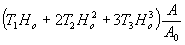 , пропорционально А и дает восстановленное изображение предмета. Наличие остальных слагаемых t
1, пропорциональных высшим степеням А, ведет к некоторым искажениям изображений первого порядка - появлению ложных изображений, фона и т.д. Что касается восстановленных волн высших порядков, то их амплитуда является функцией высших степеней А. Поэтому вид восстановленных "изображений" высших порядков существенно зависит от использованной при голографировании оптической схемы. В некоторых случаях эти "изображения" имеют очень мало сходства с голографируемым предметом. , пропорционально А и дает восстановленное изображение предмета. Наличие остальных слагаемых t
1, пропорциональных высшим степеням А, ведет к некоторым искажениям изображений первого порядка - появлению ложных изображений, фона и т.д. Что касается восстановленных волн высших порядков, то их амплитуда является функцией высших степеней А. Поэтому вид восстановленных "изображений" высших порядков существенно зависит от использованной при голографировании оптической схемы. В некоторых случаях эти "изображения" имеют очень мало сходства с голографируемым предметом.
Влияние нелинейности на изображения первого порядка. Рассмотрим член t
1еij
в уравнении (12), соответствующий восстановленной волне 1-го порядка. В соответствии с (13) его можно записать в виде
t
1eij
= a
1a×
eij
+a
2a3eij
+a
3a5eij
(14)
- 59 -
где
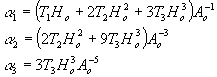 (15) (15)
Здесь коэффициенты a
1, a
2 и a
3 не зависят от координат х,у. Первым член в (14) с точностью до постоянного множителя совпадает с исходной предметной волной a×
eij
и, таким образом, образует мнимое изображение предмета. Второй член в (14) a
2А3еij
отличается от исходной предметной волны множителем a
2А2( х,у), пропорциональным экспозиции Нпр., создаваемой на голограмме одним предметным пучком
Нпр. = Епр.×
t = |
a(x,y)eij
(x,y)|
2t = a2(x,y)t (16)
Представим себе транспарант, пропускание которого является линейной функцией Нпр., т.е. Тпр.=b
А2(х,у). Волна, соответствующая члену a
2a 3e ij
, представляет собой предметную волну, прошедшую через такой транспарант. В соответствии с этим и восстановленное изображение, даваемое этим членом, будет иметь такой вид, как если бы мы смотрели на исходный предмет через пластинку с пропусканием Тпр(х,у). Вид искажений изображения при этом существенно зависит от характера Тпр(х,у). В частном случае, когда голографируемым предметом является точечный источник. расположенный на достаточно большом расстоянии от голограммы, создаваемая им освещенность в плоскости голограммы, а, следовательно, и пропускание Тпр(х,у) постоянны. При наблюдении изображения точечного источника через пластинку с постоянным пропусканием, изображение не искажается и наблюдается в том же месте, что и при линейной регистрации.
Картина существенно меняется, если предмет состоит из двух или нескольких точек. Пусть объектом голографирования является два точечных источника, расположенных в плоскости х,у, отстоящей от голограммы на расстоянии d (pис.5): r
1(х1=0, у1=b)
- 60 -
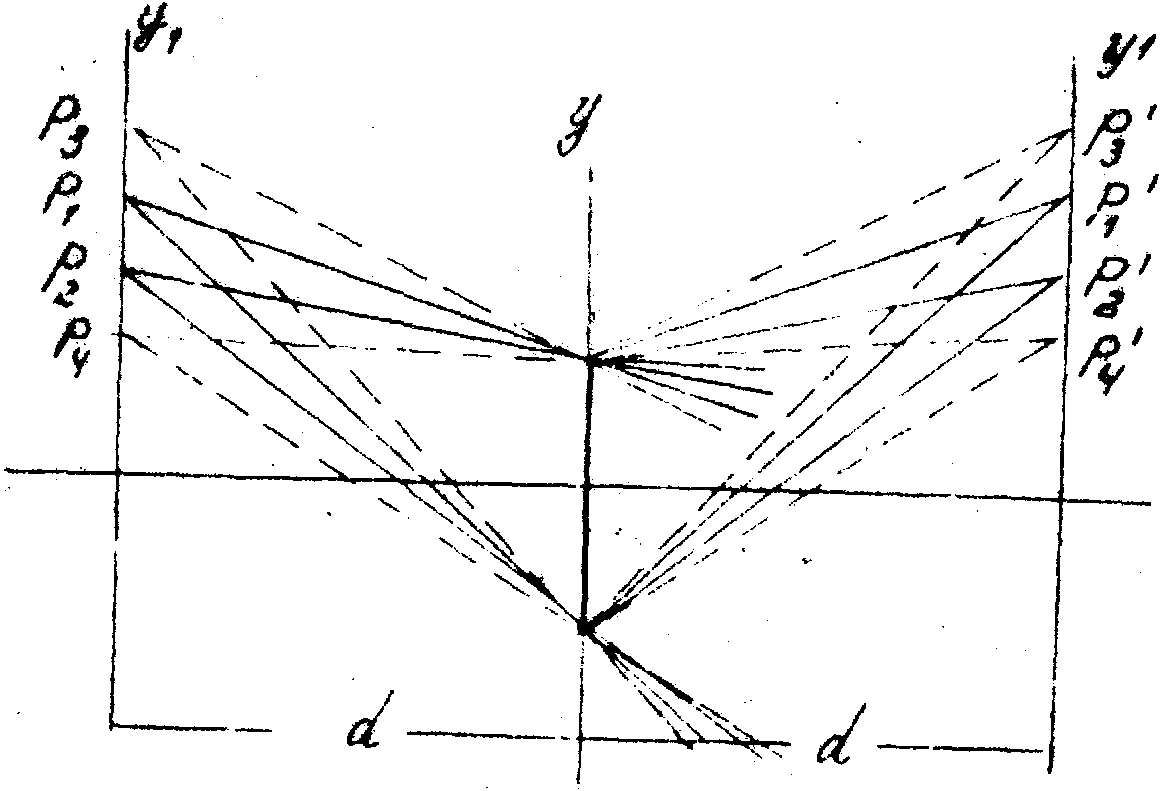
Рис.5. Появление ложных изображений в 1-ом порядке при восстановлении волновых фронтов с помощью нелинейной голограммы.
и Р 2(х1=0, у1=b-a). Волна исходящая из точки Р1, в плоскости голограммы имеет вид:
u1 = a1exp[ij
1] = a1exp[-i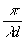 (x2+y2-2y×
b)] (x2+y2-2y×
b)] (17)
Если расстояние от Р 1 до голограммы много больше линейного размера голограммы, то А1 можно считать постоянным на поверхности голограммы. Аналогично, волну, приходящую на голограмму из точки Р2, можно представить в виде
u2 = a2exp[ij
2] = a2exp[-i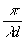 {x2+y2-2y(b-a)}] {x2+y2-2y(b-a)}] (17)
В этом случав предметная волна в плоскости голограммы имеет вид;
u = u1+u2 = a1exp[j
1]+a2exp[j
2] (19)
Восстановленная волна, соответствующая члену a
2А3e ij
, примет вид:
- 61 -
a
2 А3e ij
= a
2|
u |
2u =
= a
2(a13+2a1a22)exp[ij
1]+a
2(a23+2a1a2)exp[ij
2]+
+a
2a1a22)exp[i(2j
2-j
1)]+a
2a12a2exp[i(2j
1-j
2)] (20)
Первый и второй члены в (20) с точностью до постоянного множителя совпадают с исходными волнами (17) и (18) и дают восстановленные мнимые изображения точек Р1 и Р2. Третий и четвертый члены соответствуют ложным изображениям, расположенным по обе стороны от истинных. Действительно, фазы этих членов равны
2j
2-j
1 = -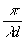 {x2+y2-2y(b-2a)} {x2+y2-2y(b-2a)}
2j
1-j
2 = -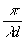 {x2+y2-2y(b+a)} {x2+y2-2y(b+a)}
и соответствуют сферическим волнам, исходящим из точек Р 3 (х1=0, у1=b+a) и Р4 (х1=0, у1=b-2a ). Таким образом, вместо двух точек, наблюдаемых при линейной записи, в случае нелинейной записи появляются четыре точки, расположенные на равных расстояниях друг от друга.
Появление ложных изображений можно объяснить также следующим образом. Как уже говорилось, изображение, даваемое членом a
2А3e ij
, имеет такой вид, как если бы мы наблюдали голографируемый объект через транспарант с пропусканием, пропорциональным освещенности А2(х,у), создаваемой в плоскости голограммы одним предметным пучком. В случае объекта, состоящего из двух точек, освещенность представляет собой периодическую структуру, возникающую при интерференции волн от двух источников. При рассматривании объекта. состоящего из двух точек, через транспарант с таким пропусканием, кроме основных точек, мы увидим добавочные точки, обусловленные дифракцией волн на периодической структуре транспаранта.
Фальшивые изображения точек, обусловленные нелинейностью голографической регистрации, впервые наблюдались Фриземом и Зеленкой /7/.
- 62 -
Помимо появления фальшивых изображений, нелинейность записи может приводить к существенному искажению относительных интенсивностей в восстановленном изображении объекта, состоящего из точек различной интенсивности. Действительно, из (20) следует, что отношение интенсивностей точек Р1 и Р2 в восстановленном изображении равно
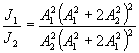 (21) (21)
Если a1>>А1, то j1/j2@
4(a1/a2)2, т.е. отношение яркостей в восстановленном изображении в 4 раза отличается от исходного. Следует отметить, что изображения точек Р1 и Р2, соответствующие нелинейному члену a
2А3e ij
в (14), накладываются на линейно восстановленные изображения точек с правильной передачей отношения интенсивностей. Таким образов, предельное искажение относительной интенсивности в 4 раза соответствует настолько сильной нелинейности, при которой вклад нелинейных членов существенно больше вклада линейного члена.
Если голографируемый объект имеет диффузно отражающую поверхность или представляет собой транспарант, перед которым помещен рассеиватель , то вид нелинейных искажений в изображении 1-го порядка можно представить себе, если, как и ранее, предположить, что линейно восстановленное изображение объекта наблюдается через транспарант с пропусканием Тпр=b
А2(х,у). Как известно, при освещении поверхности диффузно рассеянным лазерным излучением наблюдается характерная пятнистая структура. Транспарант с пропусканием, пропорциональным интенсивности этой структуры, действует как рассеиватель. При рассматривании предмета через такой транспарант контуры его размываются, появляются ореолы, сплошной фон. Таким образам, при голографировании диффузных объектов нелинейные эффекты сводятся к наложению на изображение более или менее однородного рассеянного света.
Более детальному теоретическому и экспериментального исследованию влияния нелинейности на восстановленные изображения первого порядка посвящены работы /5-8, 13, 17, 18/.
- 63 -
Влияние нелинейности на дифракционную эффективность голограммы . Исследованию влияния нелинейности на дифракционную эффективность голограмм посвящены работы Денисюка и др. /9/ и Вельцеля /11/.
Дифракционная эффективность нелинейной голограммы в n-ом порядке дифракции равна интенсивности дифрагированной волны данного порядка jn=(t
na0)2, отнесенной к интенсивности пучка используемого при восстановлении j0=a02:
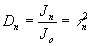 (22) (22)
где t
n определяется формулой (10) и зависит от вида функции Т[Н(j
)]. В работе /9/ были произведены расчеты t
n для случая работы в пределах линейного участка характеристической кривой, т.е. когда зависимость пропускания от экспозиции имеет вид (7). Воспользовавшись выражениями (1) и (8), экспозицию, создаваемую на голограмме опорным и предметным пучками, можно записать в виде
h = Е×
t = (А02+ А2)t(1+p ×
cos j
) (23)
Подставляя (23) в (7), получим
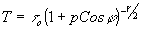 (24) (24)
где 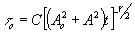 - среднее пропускание голограммы. Выражение (24) было использовано для расчетов коэффициентов t
n по формулам (10). - среднее пропускание голограммы. Выражение (24) было использовано для расчетов коэффициентов t
n по формулам (10).
Для случая линейной регистрации, когда p<<1, выражение для пропускания (24) можно разложить в степенной ряд и ограничиться членами разложения с p в первой степени:
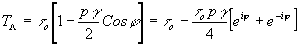 (25) (25)
Таким образом, в этом случае величина 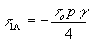 . Дифракционная эффективность линейно зарегистрированной голограммы . Дифракционная эффективность линейно зарегистрированной голограммы
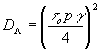 (26) (26)
- 64 -
Дифракционную эффективность нелинейной голограммы в первом порядке d1 можно записать в виде
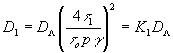 (27) (27)
где 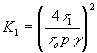 - коэффициент, характеризующий влияние нелинейности на дифракционную эффективность. Результаты расчетов К1 - коэффициент, характеризующий влияние нелинейности на дифракционную эффективность. Результаты расчетов К1, выполненных в работе /9/, приведены на рис.6-а, где величина К1,
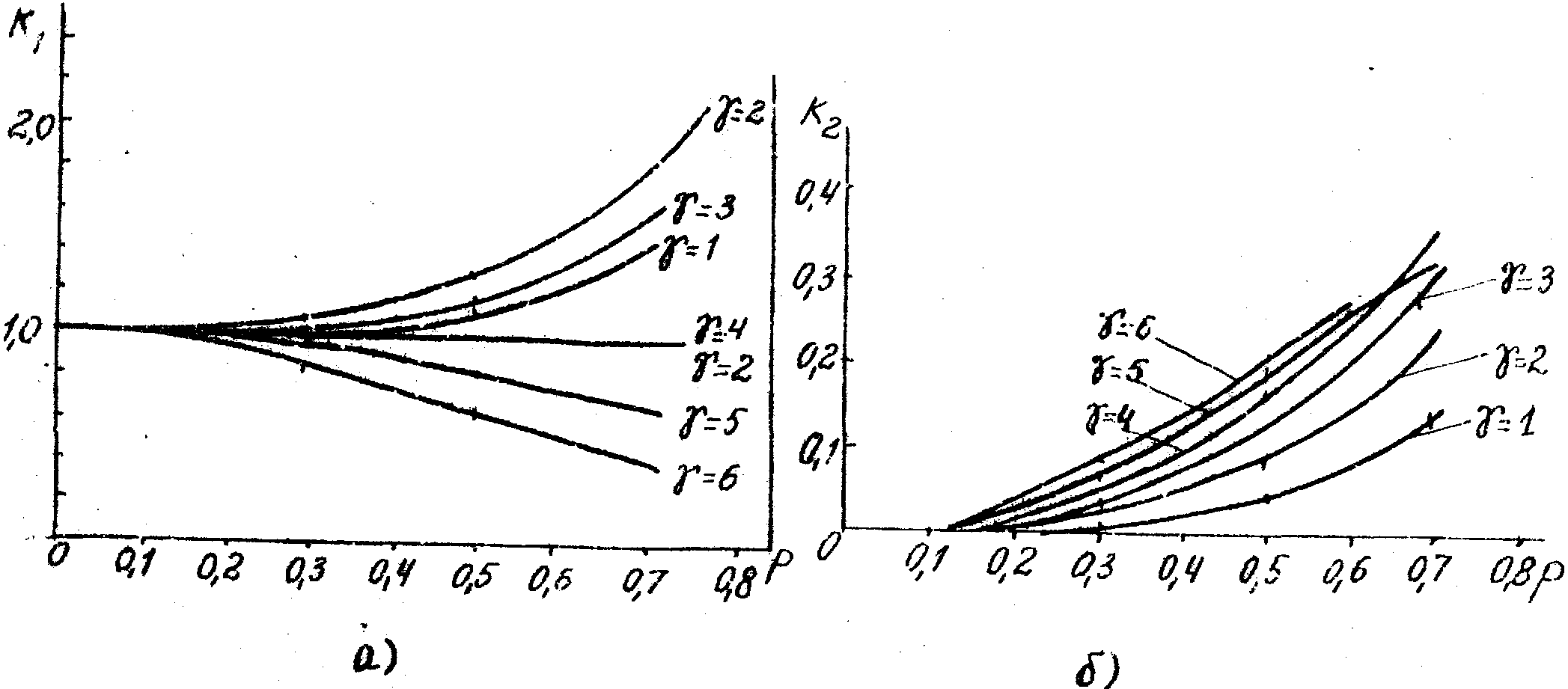
Рис.6. Влияние нелинейности на дифракционную эффективность голограммы в 1-ом (а) и во 2-ом (б) порядках.
- 65 -
представлена как функция контраста интерференционной картины p при разных коэффициентах контрастности фотоматериала g
.
По аналогии с (27) дифракционную эффективность голограммы в высших порядках можно записать в виде
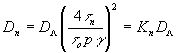 (27) (27)
Результаты расчетов К 2 как функции p при g
разных даны на рис.6б. Как и следовало ожидать, при p<<1 К2=0 , что соответствует нулевой дифракционной эффективности голограммы в высших порядках.
Следует отметить, что определению формулой (22) дифракционная эффективность соответствует полной интенсивности волны, дифрагированной в 1-ый порядок, однако, как отмечалось ранее, в восстановлении изображения участвует только часть t
1, пропорциональная А (см. формулу (14)). Остальные члены в t
1 приводят к появлению ложных изображений и рассеянного излучения, снижая контраст в истинном восстановленном изображении. Расчеты вклада этих членов в общую интенсивность излучения, дифрагированного в направлении первого порядка, приведены в работах /11, 18/.
Изображения высших порядков. В плоскости голограммы восстановленные волны 2-го и 3-го порядков описываются членами с коэффициентами t
2 и t
3, (см. формулы (12) и (13)). Фаза этих волн, соответственно в 2 и 3 раза больше, чем у исходной волны, а амплитуды их пропорциональны 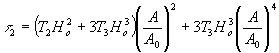 и и 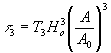 , т.е. являются нелинейными функциями амплитуды исходной волны. Таким образом, восстановленные волны высших порядков существенно отличаются от зарегистрированной на голограмме предметной волны. В соответствии с этим в общем виде трудно сказать, что представляет собой "изображение" высшего порядка, образуемое этой волной. Степень сходства этого изображения с голографируемым предметом зависит от голографической схемы в вида предмета. , т.е. являются нелинейными функциями амплитуды исходной волны. Таким образом, восстановленные волны высших порядков существенно отличаются от зарегистрированной на голограмме предметной волны. В соответствии с этим в общем виде трудно сказать, что представляет собой "изображение" высшего порядка, образуемое этой волной. Степень сходства этого изображения с голографируемым предметом зависит от голографической схемы в вида предмета.
Предметная волна u=a(x,y)eij
(x,y) может быть зарегистрирована в плоскости изображения объекта (голограмма сфокусированного изображения) во фраунгоферовой плоскости (такая схема
- 66 -
осуществляется, когда предмет находится на бесконечности или в фокусе линзы и каждая его точка посылает на голограмму параллельный световой пучок) и, наконец, в любой промежуточной плоскости. В этом случае волна u(x,y) в плоскости голограммы представляет собой френелевскую дифракционную картину.
Наиболее простым является, очевидно, случай голограммы сфокусированного изображения. При этом функция предметной волны u(x,y) представляет собой распределение амплитуды и фазы не только в плоскости голограммы, но и в плоскости изображения объекта. Восстановленная волна второго порядка имеет вид:
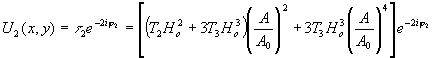 (29) (29)
Восстановленное изображение второго(и высших) порядка локализовано в плоскости голограммы и описывается функцией u2(х,у) Как видно, распределение амплитуд в изображении высших порядков существенно отличается от соответствующего распределения на поверхности предмета. Тем не менее, поскольку имеется однозначная связь между t
2 и А, то изображение имеет полное сходство с объектом. (Искажения аналогичны тем, которые имеют место при фотографическом получении изображения предмета. В этом случае яркость предмета и изображения всегда связаны нелинейной зависимостью).
Если объект чисто фазовый, т.е. амплитуда a(x,y)=const, то величина t
2 также не зависит от координат и восстановленная волна отличается от исходной только постоянным коэффициентом и удвоением фазового сдвига.
Для случая, когда голограмма зарегистрирована во фраунгоферовой плоскости, предметная волна u(х,у) в плоскости голограммы представляет собой преобразование Фурье функции y
(х,у ), соответствующей распределению амплитуды и фазы в непосредственной близости к голографируемому предмету
u(x,y) = ò
ò
¦
(x1,y1)exp[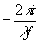 (x1x+y1y]dx1dy1 (x1x+y1y]dx1dy1 (30)
- 67 -
Процесс восстановления изображения с помощью фраунгоферовой голограммы также представляет собой преобразование Фурье амплитудного пропускания голограммы
f(x1,y1) = ò
ò
t(x,y)exp[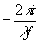 (xx1+yy1]dxdy (xx1+yy1]dxdy (31)
Здесь f(x1,y1) - восстановленная волна в плоскости изображения. При линейной регистрации, когда один из членов амплитудного пропускания пропорционален u(x,y), в результате такого дважды повторенного преобразования Фурье для части t(х,у) пропорциональной u(x,y), получается функция f1(x1,y1), с точностью до постоянного множителя совпадающая с исходной функцией в плоскости объекта ¦
(x1,y1), что и соответствует восстановлению изображения предмета.
При нелинейной регистрации связь амплитудного пропускания о амплитудой и фазой предметной волны u(x,y)=a(x,y)exp[ij
] дается формулами (12,13). Члены пропускания, соответствующие высшим порядкам дифракции, пропорциональны u2(х,у), u3(х,у) и другим функциям типа (uu*)u2, (uu*)u*2 и т.д. В частности, член пропускания
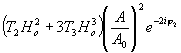
определяющий главную часть восстановленной волны 2-го порядка, пропорционален u2(х,у). Таким образом, восстановленное изображение 2-го порядка f2(x,y) будет теперь описываться выражением (31), в котором вместо Т(х,у) подставлена величина c'u2(x,y), где c'=const, a u(x,y) связано с ¦
(x1,y1) преобразованием Фурье (30). Можно показать, что f2(x1,y1) в этом случае пропорционально автосвертке функций ¦
(x1,y1)
f2(x1,y1)~ò
ò
¦
(x,y)¦
(x1-x,y1-y)dxdy (32)
Для случая диффузно отражающего объекта или при съемке голограммы с рассеивателем, фаза волны ¦
(x1,y1) беспорядочно меняется от точки к точке и автосвертка имеет мало общего с исходной
- 66 -
волной ¦
(x1,y1).
Рассмотрим теперь наиболее часто встречающийся случай , когда объект помещен на некотором расстоянии d от голограммы. Тогда предметная волна в плоскости голограммы u(х,у) является френелевским преобразованием волны ¦
(x1,y1):
u(x,y)=ò
ò
¦
(x1,y1)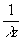 exp[ exp[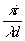 {(x1-x)2+(y1-y)2}]dx1dy1 {(x1-x)2+(y1-y)2}]dx1dy1 (33)
а восстановленная волна в плоскости мнимого изображения f2(x1',y1') (x1' и y1' - координаты в плоскости, отстоящей от голограммы на расстоянии z) также связана с амплитудным пропусканием голограммы преобразованием Френеля:
f2(x1',y1')=ò
ò
t(x,y)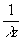 exp[ exp[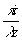 {(x1'-x)2+(y1'-y)2}]dxdy {(x1'-x)2+(y1'-y)2}]dxdy (34)
Можно показать, что наиболее простая связь между функцией "изображения" 2-го порядка f2(x1',y1') и функцией предмета ¦
(x1,y1), будет в том случае, когда "изображение" получается в плоскости 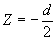 . В этом случае . В этом случае
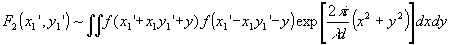 (35) (35)
В качестве примера рассмотрим случай, когда предметом является точечный источник, помещенный в плоскости z=-d в т. p1(x1=0, y1=b, z=-d). Тогда в плоскости голограммы предметная волна имеет вид (18):
u(x,y) = a×
exp[ij
1] = a×
exp[-i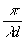 {x2+y2-2y×
b}] {x2+y2-2y×
b}] (36)
а функция u2 равна
u2(x,y) = a2exp[-i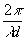 {x2+y2-2y×
b}] {x2+y2-2y×
b}] (37)
- 69 -
т.е. представляет собой тоже сферическую волну, но исходящую из точки Р 2(x 1'=0, у1'=b, z=- 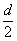 ) (см. рис.7). Эта волна и будет восстановлена во втором дифракционном порядке. Аналогичным образом в 3-ем порядке восстановится волна
u3(x,y) = a3exp[-i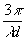 {x2+y2-2y×
b}] {x2+y2-2y×
b}] (37)
и восстановленное в 3-ем порядке изображение точечного источника будет находиться в точке Р 3(x 1'=0, у1'=b, z=- 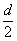 ).
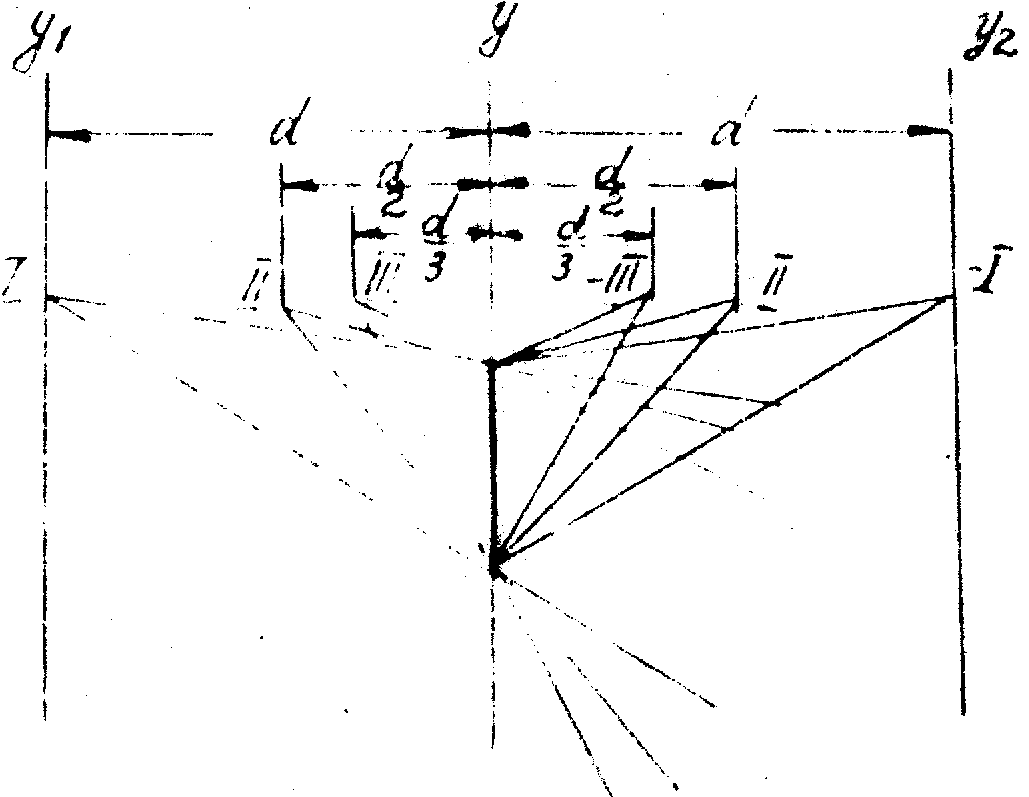
Рис. 7. Образование изображении точечного источника в высших дифракционных порядках.
Детальному теоретическому и экспериментальному исследованию изображений высших порядков посвящена работа Брингдала и Ломанна /15/, в которой показано, что в тех случаях, когда голографируемым объектом является транспарант (изображение яркой буквы на темном фоне) , расположенный на сравнительно небольшом расстоянии d от голограммы (l
d меньше размеров объекта), и голограмма получается без рассеивателя, изображения высших порядков практически не отличаются от изображения первого порядка. Картина резко меняется, когда перед транспарантом помещен рассеиватель. В этом случае "изображения" высших порядков весьма отдаленно напоминают исходный предмет.
Использование нелинейных эффектов для увеличения чувствительности голографической интерферометрии. Увеличение фазы восстановленной волны в высших порядках в n раз (n - номер порядка) по
- 70 -
сравнению с фазой волны в первом порядке позволяет использовать восстановленные волны высших порядков для увеличения чувствительности голографической интерферометрии /19-21/.
При голографировании фазового объекта, вносящего в проходящую через него плоскую волну небольшие фазовые искажения, амплитуда объектного пучка сравнительно слабо меняется на поверхности голограммы и коэффициента t
о, t
1, t
2, и t
3 (см. формулу (13)) можно считать постоянными. Фазу предметной волны можно представить в виде двух слагаемых:
j
= 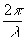 y×
sina
+d
(x,y) y×
sina
+d
(x,y) (39)
где 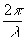 y×
sina
- фаза плоской, просвечивающей фазовый объект волны, падающей на голограмму под утлой a
, и d
(х,у) - фазовые искажения, вносимые в волну исследуемым объектом. Если осветить голограмму, с пропусканием, oпиcывaeмым уравнением (12), двумя плоскими волнами единичной амплитуды, одна из которых ¦
1 падает нормально к поверхности голограммы, а другая y×
sina
- фаза плоской, просвечивающей фазовый объект волны, падающей на голограмму под утлой a
, и d
(х,у) - фазовые искажения, вносимые в волну исследуемым объектом. Если осветить голограмму, с пропусканием, oпиcывaeмым уравнением (12), двумя плоскими волнами единичной амплитуды, одна из которых ¦
1 падает нормально к поверхности голограммы, а другая
¦
2 = exp[ij
2] = exp[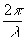 y×
sinb
] y×
sinb
]
под углом b
=-arcsin(k×
sina
), то в направлении нормали к голограмме будут распространяться две волны - нулевого порядка для ¦
1 и k-го порядка для
¦
2(¦
2'=t
k×
exp[i×
kj
+ij
k]=t
k×
ei×
kd
(см. рис.8а). В результате интерференции этих волн возникнут полосы, смещение которых пропорционально Кd
, т.е. в К раз больше, чем на обычной интерферограмме.
Если на голограмму направить две волны под углами b
1,2= ±
arcsin(k ×
sin a
), то в направлении нормали будут распространяться волна k-го порядка для одной из этих волн а +k-го - для другой (см. рис.8б). В результате их интерференции получатся полосы, соответствующие разности фаз 2Кd
.
В работе /21/ описанным способом было достигнуто 14-кратное увеличение чувствительности голографической интерферометрии.
Следует отметить, что при данном методе увеличения чувствительности усиливаются не только искажения волнового фронта, вносимые
- 71 -.
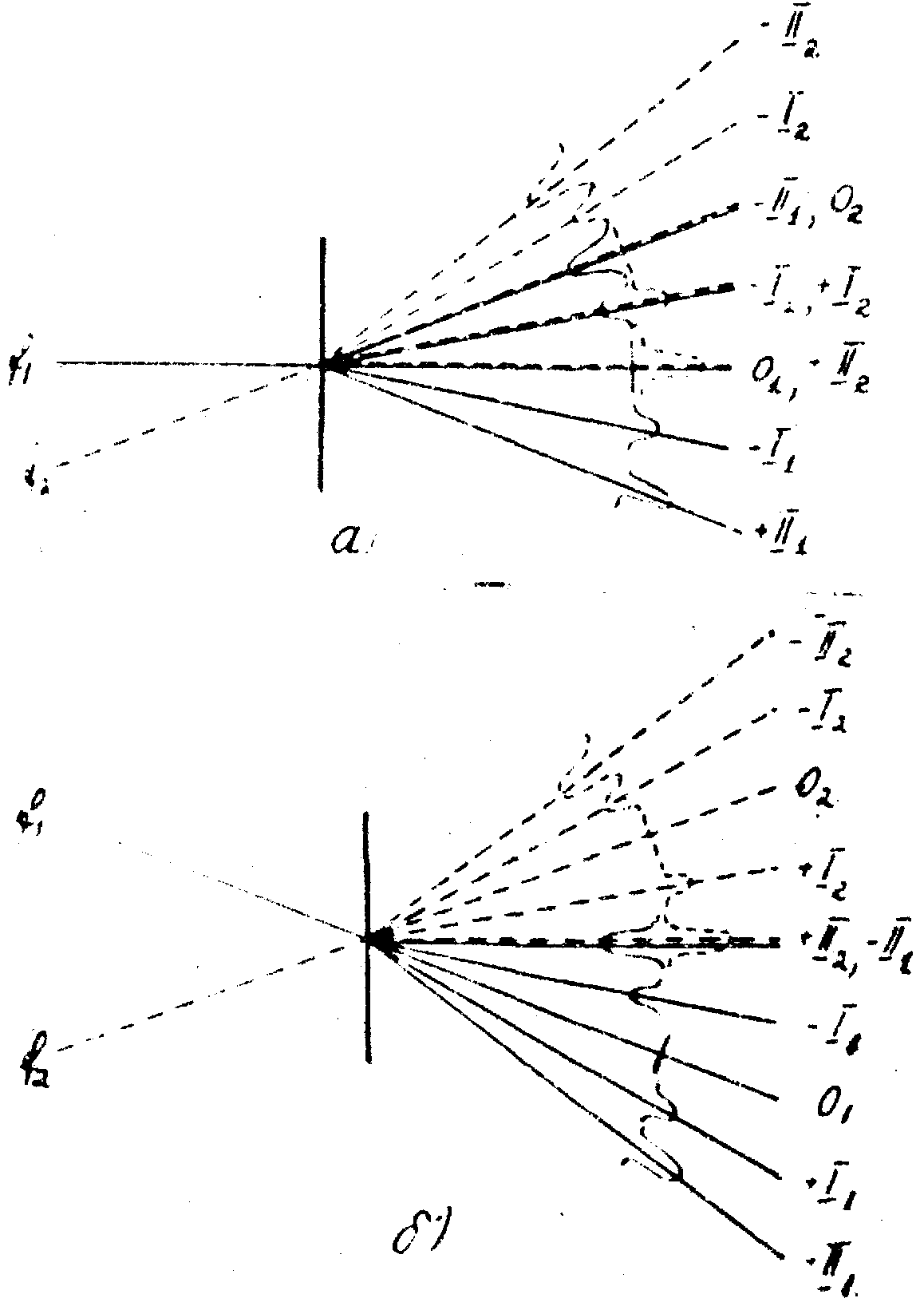
Рис.8. Схемы увеличения чувствительности голографической интерферометрии: а - при интерференции волн 0-го и k-го порядков, б - при интерференции волн +К -го и -k-го порядков.
исследуемым объектом, но и любые искажения , обусловленные несовершенством оптических элементов голографической установки. Поэтому голографические схемы, предназначенные для увеличения, чувствительности обычно создаются на базе интерферометров. Кроме того, следует помнить, что изображения высших порядков в схемах с использованием рассеивателя имеют мало общего с объектом. Поэтому голограмма должна быть либо зарегистрирована в плоскости изображения (голограмма сфокусированного изображения), либо в схеме без
- 72 -
рассеивателя.
Как известно, голографические интерферограммы, полученные методом двух экспозиций, нечувствительны к качеству оптических деталей голографической установки. Однако использование этого метода при восстановлении интерферограммы в высших порядках связано с рядом трудностей, обусловленных тем. что в направлении волновых фронтов k-го порядка для двух волн, зарегистрированных при двух последовательных экспозициях, распространяются также волны с фазами ℓj
1+m j
2, где m+ℓ=k, а j
1 и j
2 – фазы волн при двух экспозициях. Наложение этих волн существенно искажает наблюдаемую интерференционную структуру. На возможные пути преодоления этих трудностей указывается в работе /22/, где методом двухэкспозиционной голографической интерферометрии с восстановлением интерферограмм в высших порядках достигнуто 4-кратное увеличение чувствительности измерений распределения плотности газа внутри сосуда с неоднородными стенками.
Дисперсионная двухдлинноволновая голографическая интерферометрия. Другой вариант голографической интерферометрии с использованием высших (2-ых) порядков дифракции описан в работах /23-24/, где предложен метод получения интерферограмм, форма полос на которых определяется только различием показателей преломления среды для излучений с двумя длинами волн, т.е. дисперсией исследуемого объекта.
Метод состоит в следующем: голограмму получают в свете излучения с двумя длинами волн, отличающимися ровно в два раза (l
1=2l
2), причем, утлы падения опорных и предметных пучков на голограмму для обеих длин волн одинаковы (рис.9а). Голограмму регистрируют на нелинейном фотоматериале. Тогда при восстановлении световых волн с помощью такой голограммы для каждой из присутствующих в излучении длин волн восстановятся волны ±
1-го, ±
2-го, ±
3-го и т.д. порядков (рис.9б). При этом волна 2-го порядка для голограммы, полученной в свете l
1, будет распространяться под тем же углом, что и волна 1-го порядка, соответствующая голограмме, полученной в свете l
2.
Фазовые искажения, вносимые в волну исследуемым объектом, для l
2 в 1-ом дифракционном порядке равна 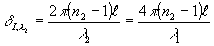
- 75 -
а фазовые искажения для l
1 во 2-ом порядке
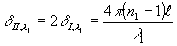
Здесь ℓ - толщина объекта, n1 и n2 - его показатель преломления для излучений с длинами волн l
1 и l
2. При условия, что n1=n2, равны и сдвиги фаз 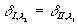
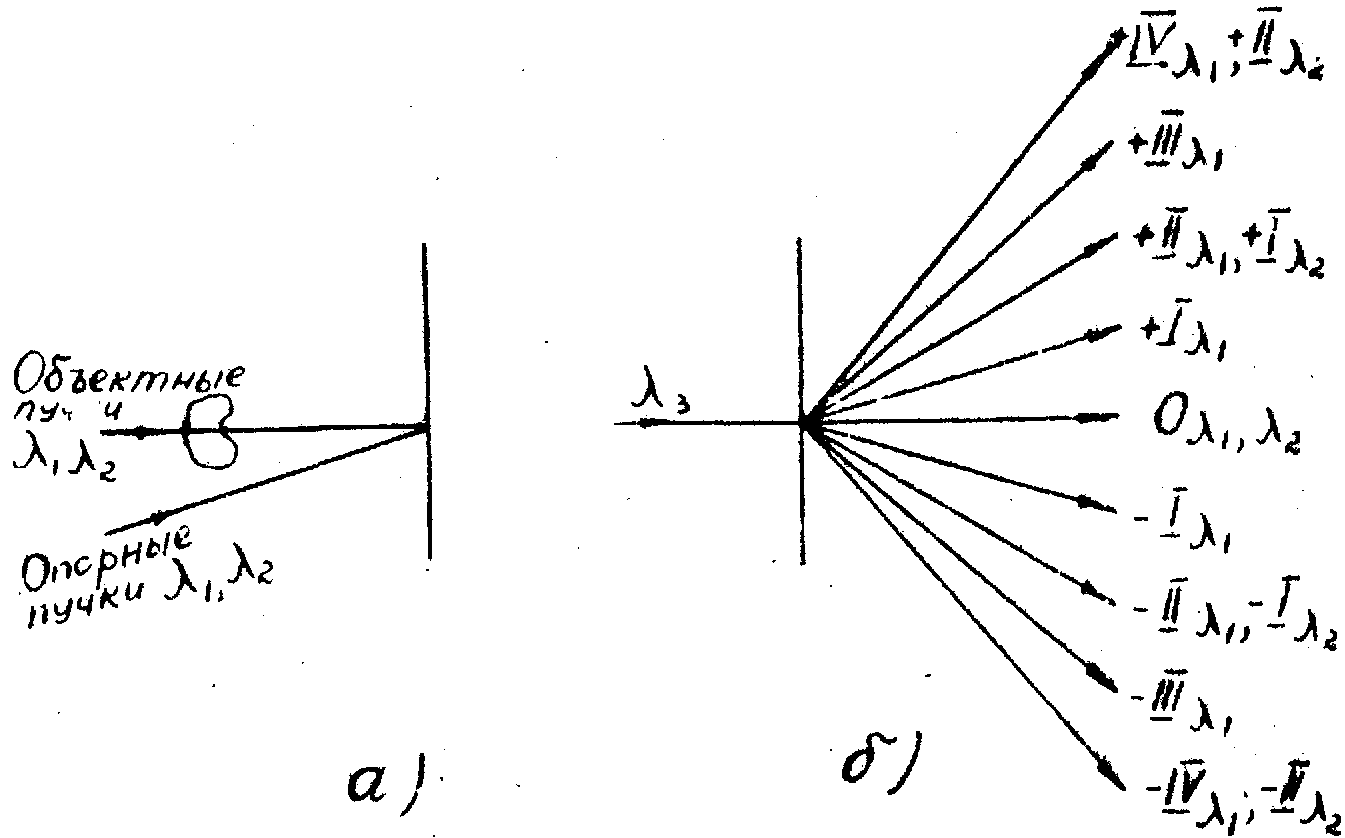
Рис.9. Схема получения двухдлинноволновой голограммы (l
1=2l
2) (а) и дифракция световой волны на двухдлинноволновой нелинейной голограмме в процессе восстановления (б).
Различие фазовых искажений, а следовательно, и пространственная частота интерференционных полос, будет, таким образом, определяться только различием показателя преломления среды для излучений с длинами волн l
1 и l
2, т.е. дисперсией среды
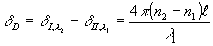 (40) (40)
Особый интерес представляет использование этого метода для
- 74 -
диагностики плазмы. Если пренебречь слабой зависимостью поляризуемости атомов от длины волны вдали от линии поглощения, то можно считать, что дисперсия плазмы определяется только плотностью электронного газа:
n2-n1 = 4,5×
10-14(l
12-l
22)ne (41)
Дисперсионный метод позволяет по одной голографической интерферограмме определить величину n2-n1, непосредственно связанную с концентрацией электронов в плазме. В то же время метод полностью нечувствителен к фазовым искажениям, обусловленным перераспределением тяжелых частиц в зоне плазмы, поскольку показатель преломления в этом случае практически не зависит от длины волны.
Некоторые другие возможные применения нелинейных аспектов. Как было показано ранее (см. формулы (14) и (15)), член в пропускании голограммы, соответствующий восстановленной волне 1-го порядка t
1e ij
является нелинейной функцией амплитуды предметной волны
t
1eij
= [d1+a
2a2+a
3a4]a×
eij
Таким образом, если амплитуда предметной волны значительно меняется на поверхности голограммы , то степень нелинейных искажений, вносимых в волновой фронт разным участками голограммы различна.
Если голограмма расположена в фурье-плоскости (т.е. в фокальной плоскости линзы с фокусом ¦
), то предметная волна u(x,y) представляет собой спектр пространственных частот объекта. Как правило, высокочастотной составляющей соответствуют малые амплитуды, для которых экспозиции не выходят за линейную часть кривой Т(Н) и поэтому они передаются без искажений. Подбирая величину Но (экспозицию опорного пучка) и максимальную освещенность, создаваемую предметной волной в плоскости голограммы, можно добиться значительного подавления низкочастотной части пространственного спектра объекта. Это свойство нелинейно зарегистрированной голограммы может быть использовано для пространственной фильтрации /25,26/
В работе Геритсена /27/ обсуждается возможность использования нелинейных эффектов для получения топографическим методом увеличенных изображений с правильным соотношением продольного и
- 75 -
поперечного размеров.
В заключение укажем также на работу Шнидера и Бурова /28/ , где нелинейная запись голограммы используется для получения изофот (кривых равной яркости), а также на работы Мацумото /29,30/ и Брингдала /31/, в которых волны высших порядков, восстановленные нелинейной голограммой, использовались для получения многолучевых голографических интерферограмм.
Литература
1. А.П.Комар, М.В.Стабников, Б.Г.Турухано. ДАН, 169, 1052, 1966.
2. c.clausen, h.dammann. opt.commun., 2, 263, 1970.
3. c.s.vikram, r.s.sirohi. opt.commun., 2, 444, 1970.
4. r.s.sirohi, c.s.vikram, opt.commun., 3, 122, 1971.
5. j.m.j.tokarski. appl.opt., 7, 989, 1968; 8, 1510, 1969.
6. a.kozma. journ.opt.soc.am., 56, 428, 1966.
7. a.a.friesem. j.s.zelenka. appl.opt., 6, 1755. 1967.
8. g.r.knight. appl.opt., 7, 205, 1968.
9. Ю.Н.Денисюк, Г.Б.Семенов, Н.А.Савостьяненко. Опт. и спектр. 29, 994, 1970.
10. j.upatnieks, c.d.leonard, appl.opt., 10, 2365, 1971.
11. c.h.f.velzel. opt.commun., 3, 133, 1971.
12. Дж.Гудмен. Введение в фурье-оптику. Изд. "Мир", М., 1970.
13. j.w.goodman, g.r.knight. journ.opt.soc.am., 58, 1276, 1968.
14. j.schwider. r.burov. exp.tech.physic, 18, 255, 1970.
15. o.bryngdal, a.lohmann, journ.opt.soc.am., 58, 1325, 1968.
16. r.j.collier, c.b.burckhardt, l.h.lin. optical holography, n.y. -london, 1971.
17. j.c.wyant, m.p.givens. appl.opt., 9, 810, 1970.
18. a.kozma, g.v.jull, k.o.hill. appl.opt., 9, 721, 1970.
19. o.bryngdal, a.w.lohmann. journ.opt.soc.am., 58, 141, 1968/
20. К.С.Мустафин, В.А.Селезнев. Е.И.Штырков. Опт. и спектр, 28, 1186. 197.
21. k.matsumoto, m.takashima. journ.opt.soc.am., 60, 30, 1970.
22. c.h.f.velzel. opt.commun., 2, 289, 1970.
23. Г.В.Островская, Ю.И.Островский. ЖТФ, 40, 2419, 1970.
- 76 -
24. А.Б.Игнатов, И.И.Комиссарова, Г.В.Островская, Л.Л.Шапиро ЖТФ, 41, 417, 1971.
25. В.Н.Славянская. Опт. и спектр. 31, 986, 1971.
26. a.vander lugt, f.b.rotz. appl.opt., 9, 215, 1970.
27. h.j.gerritsen, appl.pnys.lett., 10, 239, 1967.
28. j.schwider, r.burov. journ.opt.soc.am., 60, 1421, 1970,
29. k.matsumoto, journ.opt.soc.am., 59, 777, 1969
30. k.matsumoto, journ.opt.soc.am., 61, 176, 1971
31. o.bryngdal. journ.opt.soc.am., 59, 1171, 1969.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

