|
|
 |
 |

|
| |
дифраКЦИЯ когЕрЕНтного сВЕтА В срЕдЕ с прострАНстВЕНно-ПЕРИОдИЧЕСКИМ РАСПРЕДЕЛЕНИЕМ ПОКАЗАтЕЛЯ ПРЕЛОМЛЕНИЯ
Н.М.Померанцев
Рассмотрена дифракция света в толстом прозрачном слое с периодическим распределением показателя преломлении.
Установлена зависимость дифракционной эффективности такой фазовой синусоидальной решётки от её пространственной частоты. Кривые этой зависимости, названные диаграммами направленности, рассчитаны для ряда практически важных случаев.
Введение
Практическое значение дифракции света в последние годы значительно возросло благодаря развитию и совершенствованию методов голографии. Что же касается самой голографии, то ее практическое значение в сильной степени зависит от того, какая часть световой энергий в реальной голограмме падает на долю изображения при восстановлении. Это качество голограмм характеризуется ее дифракционной. эффективностью /1/, которая определяется как отношение интенсивности излучения в первом порядке дифракции к полной интенсивности излучения, падающего на голограмму */. Предполагается, что голограмма представляет собой дифракционную решетку, полученную с помощь интерференции двух плоских волн.
Дифракционная эффективность зависит от применяемого для регистрации голограмм материала и изменяется при изменении углов, под которыми плоские волны падают при записи на голограмму. Другими словами, дифракционная эффективность является функцией пространственной частоты решетки.
* Ниже мы увидим, что это определение нуждается в небольшом уточнении .
- 23 -
Здесь мы рассмотрим зависимость дифракционной эффективности только от свойств самой голограммы, не касаясь влияния фотоматериала.
Голограммы, как известно, могут быть разделены с одной стороны на амплитудные и фазовые, а с другой - на тонкослойные и толстослойные. С точки зрения дифракционной эффективности наибольший интерес представляют толстослойные фазовые голограммы, которые в основном и будут здесь рассмотрены. Критерий, по которому удобно производить разделение голограмм на толстослойные и тонкослойные, будет рассмотрен особо.
Конечной целью рассмотренного ниже исследования дифракции света в толстых слоях является установление зависимости дифракционной эффективности голограммы от пространственной частоты голографируемого предмета.
Для такого исследования удобно представить толстослойную голограмму как линейную систему, преобразующую по определенному закону поступающие на нее сигналы. Рассматривается одна составляющая ряда (или интеграла) Фурье исходного сигнала и исследуется зависимость интенсивности этой составляющей на выходе системы от пространственной частоты. В результате какого исследования мы получим частотную характеристику дифракционной эффективности толстослойной голограммы. Так как разложение по пространственным частотам является в одно и то же время разложением по плоским волнам, распространяющимся в пространстве под разными углами, то такую характеристику можно назвать диаграммой направленности толстослойной голограммы. Заметим, что для тонкослойных голограмм направления всех плоских волн, на которые можно разложить сложную волну, исходящую от предмета, равноправны, если не учитывать влияния материала, и в диаграмме направленности нет необходимости.
Таким образом, мы должны рассмотреть дифракцию на толстослойной фазовой дифракционной решетке, записанной с помощью двух плоских волн: опорной и предметной. При воспроизведении используется одна плоская волна, падающая, как правило, под тем же углом, что и опорная при записи. Мы будем варьировать угол, под которым падает на решётку предметная волна, и искать зависимость дифракционной эффективности от величины этого угла. Это и будет
- 24 -
искомая нами частотная характеристика дифракционной эффективности или диаграмма направленности толстослойной голограммы.
Необходимо отметить, что дифракционная эффективность не является полной характеристикой голограммы. Зависимость дифракционной эффективности от пространственной частоты не включает фазовых соотношений между компонентами спектра пространственных частот. Однако при суммировании отдельных компонент в изображении фазовые соотношения между ними играют существенную роль. Поэтому в дополнение к частотной зависимости дифракционной эффективности необходимо рассматривать еще зависимость фазы плоской волны от пространственной частоты.
1. Параметры фазовой дифракционной решетки, полученной с помощью интерференции двух плоских волн
Рассмотрим пространственную (трехмерную) интерференционную картину, полученную в результате сложения двух плоских волн: опорной j1=a×
exp[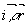 ] и предметной j2=b×
exp[ ] и предметной j2=b×
exp[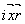 ], где А и В -амплитуды волн, ], где А и В -амплитуды волн, 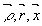 - векторы, - векторы,
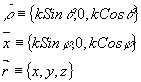
Направления распространения волн и углы q
и j
представлены на рис.1.
Интенсивность i=(j1+j2)(j*1+j*2) суммарной волны может быть представлена следующим образом:
i = a2+b2+2×
a×
b×
cos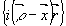 . .
Первое слагаемое в этом выражении является квадратом амплитуды спорной волны и не зависит от угла q
.
Второе слагаемое является квадратом амплитуды предметной волны, в качестве которой мы взяли только одну Фурье -составляющую излучения, исходящего от предмета. Так как разные Фурье-составляющие имеют разную величину в зависимости от угла j
, то
- 25 -
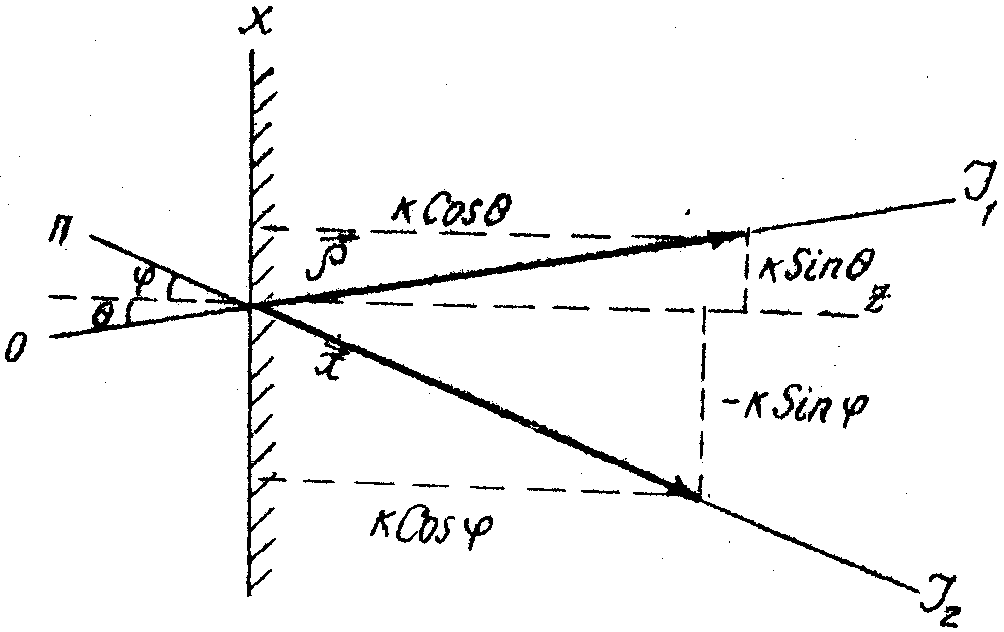
Рис.1. Волновые векторы предметной и опорной волны, координаты векторов и углы падения воли на светочувствительный слой.
величина В 2 будет функцией угла У Низкочастотная составляющая этой функции В2=b 2( j
) в случае фазовых голограмм, накладываясь на изображение при восстановлении, создает блики вокруг изображения, уменьшающие его контраст. Это - существенный недостаток фазовых голограмм. Однако имеются методы уменьшения помех такого рода. Рассмотрение этих методов не относится к теме лекции. Отметим однако, что одним из условий получения приемлемой величины отношения сигнал/шум является условие малости величины В2 по сравнению с А2, т.е. должно соблюдаться условие А2>> В2, которое мы в дальнейшем используем.
Не рассматривая конкретных свойств фоторегистрирующего материала, предположим, что в результате освещения голограммы двумя пучками лучей и последующей обработки произойдут изменения диэлектрической проницаемости, пропорциональные интенсивности света, попавшего в, ту или иную точку фотоматериала. Поэтому можно принять, что диэлектрическая проницаемость фотоматериала после записи на нем дифракционной решетив будет зависеть от координат следующим образом:
e
= e
о+D
e
cos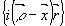
- 26 -
Если принять во внимание приведенное выше неравенство (А 2>> В2), из которого следует, что D
e
/e
о<<1, то для константы распространения 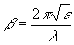 получим выражение; получим выражение;
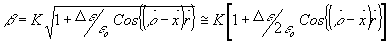
где 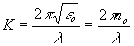
Таким образом, характеристики фазовой дифракционной решетки определяются тремя параметрами: углом падения опорного луча q
, углом падения предметного луча j
и максимальной величиной относительного изменения диэлектрической проницаемости D
e
/e
о. При такой форме зависимости диэлектрической проницаемости от координат можно учесть также и поглощение в голографическом слое, если заменить величины e
о и D
e
соответствующими комплексными величинами. Мы, однако, будем считать e
о и D
e
, действительными.
В некоторых случаях угол падения пучка лучей света на решетку при дифракции (при воспроизведении голограммы) отличается от угла падения опорного пучка лучей при записи. Тогда появляется четвертый параметр v угол падения света на решетку при дифракции.
2. Методы решения задачи
Теория дифракции света в толстых слоях развивалась несколькими почти независимыми путями. Существует, по крайней мере, четыре метода решения задачи о дифракции света в толстых слоях с периодическим законом распределения показателя преломления к коэффициента поглощения.
1. Кинематическая теория. В ее основу положен принцип Гюйгенса и предположение о малости амплитуды дифрагировавших волн по сравнению с падающим на дифракционную решетку излучением. Задача решается методом возмущений.
2. Динамическая теория. В этой теории решаются уравнения Максвелла для распространения электромагнитных волн в толстых средах. Теория имеет также приближенный характер, так как окончательное
- 27 -
решение получено только в двухволновом приближении.
Как кинетическая, так и динамическая теории были разработаны при изучении дифракции рентгеновских лучей в кристаллах.
3. Теория связанных волн. Она также основана на решении уравнений Максвелла, но применение специального вида разложения в ряд Фурье приводит к системе уравнений, подобной системе, описывающей колебания связанных резонаторов. Задача решена для двух предельных случаев, охватывающих две области дифракции. Эта теория была разработана для объяснения дифракции света на ультразвуковых волнах.
4. Решение с помощью ЭВМ. Получены точные решения уравнений Максвелла для ряда частных случаев.
Мы остановим свое внимание на теории связанных волн /2/. Эта тория позволяет выявить зависимость характера дифракции от толщины слоя и проследить за перераспределением интенсивности света по порядкам дифракции при его распространении внутри среда в процесса дифракции.
Переходим к рассмотрении теории.
Стационарные уравнения Максвелла для изотропной немагнитной среды имеют вид:
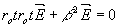
Приняв во внимание установленную выше зависимость диэлектрической проницаемости от координат, постоянную распространения b
можно в нашем случае представить следующим образом:
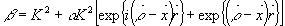
где 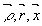 - векторы, определенные выше, - векторы, определенные выше,
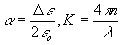
Применяя метод связанных волн, будем искать решение приведенных выше уравнений в виде следующего ряда Фурье:
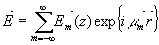
- 28-
Векторы 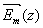 - подлежащие определению функции, предполагаются зависящие только от переменной z, так как имеется в виду, что зависимость - подлежащие определению функции, предполагаются зависящие только от переменной z, так как имеется в виду, что зависимость 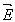 от x чисто периодическая, вследствие периодичности структуры и неограниченности размеров дифракционной решетки в направлении оси x. от x чисто периодическая, вследствие периодичности структуры и неограниченности размеров дифракционной решетки в направлении оси x.
Нетрудно убедиться, что с помощью такого ряда Фурье из уравнений Максвелла можно получить систему уравнений с постоянными коэффициентами. Для этого надо определить векторы и. следующим образом :
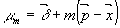
где 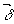 - волновой вектор падающей на решетку исходной волны, - волновой вектор падающей на решетку исходной волны,
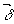
º
{к×
sinu
;0;к×
cosu
}
u
- угол падения исходной волны на решетку. Если восстанавливающая волна падает на решетку в том же направлении, что и опорная при записи, то 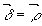 и u
=q
. и u
=q
.
При значениях 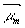 , определенных выше, решение примет вид: , определенных выше, решение примет вид:
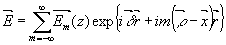
Физический смысл этого решения заключен в том, что внутри среды (т.е. после прохождения волной границы раздела), кроме волны, совпадающей по направлению с исходной, 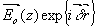 , возникает бесконечный ряд дифрагировавших волн, , возникает бесконечный ряд дифрагировавших волн,
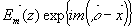
расположенных веером по обе стороны от исходной.
Амплитуды и фазы дифрагировавших волн зависят от z , так как волны при распространении внутри среды взаимодействуют друг с другом. Это взаимодействие возникает вследствие того, что волны при прохождении слоистой структуры периодически испытывают отражение и преломление. Благодаря периодичности отражений и преломлений, а также интерференции, распространение света в среде происходит
- 29 -
только по определенным направлениям, т.е. энергия "канализуется" , так что переходы энергии из одного канала в другой, обусловленные отражением и преломлением, возможны только между соседними каналами. Расположение каналов показано на рис.2. На нем изображены волновые векторы нескольких первых порядков, причем, показан случай, когда направление волны, падающей на решетку при восстановлении, совпадают с направлением опорной волны при записи.
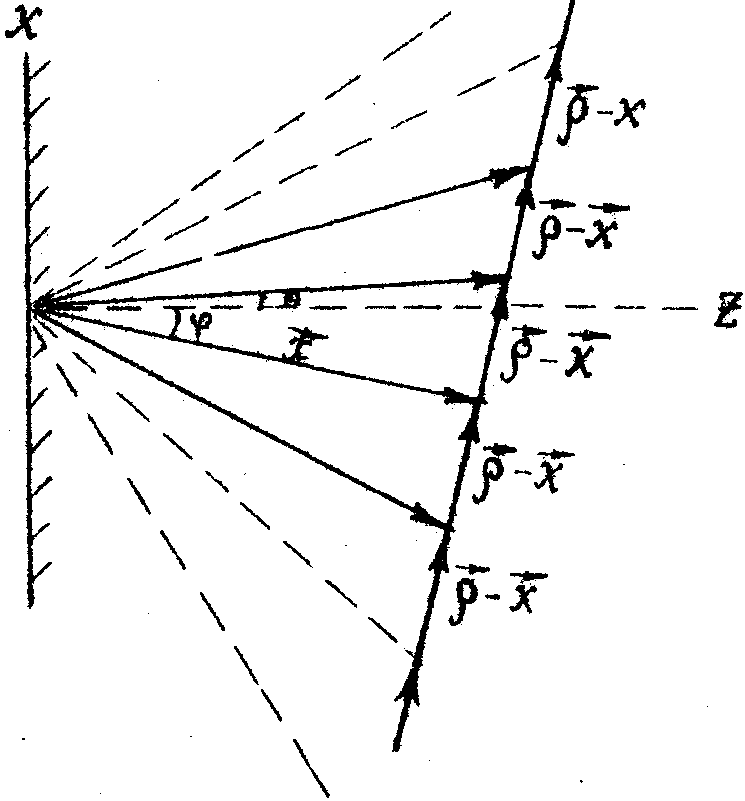
Рис.2. Направления распространения дифрагировавших волн внутри среды.
Для того, чтобы получить систему уравнений, имеющую удобный для решения вид, сделаем одно предположение, на ограничивающее общности решения. Предположим, что в процессе дифракции поляризация волн не меняется. Такое предположение вполне законно для изотропных сред. Тогда можно принять
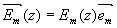
где em(z) - скалярная функция, 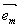 - единичный вектор, не - единичный вектор, не
- 30 -
зависящий от z, лежащий в плоскости поляризации и перпендикулярный направлению распространения волны. Благодаря этому для векторов 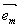 действительны соотношения: действительны соотношения:
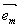 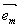
= 1; 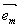 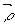 = 0 = 0
В результате подстановки ряда Фурье в уравнения Максвелла с учетом всех приведенных соотношений получим для em(z) систему однородных уравнений с постоянными коэффициентами:
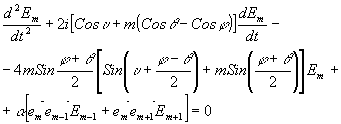
где введена новая переменная t = к×
z
Величина скалярного произведения 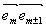 зависит от ориентации вектора исходной волны зависит от ориентации вектора исходной волны 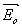 . Если этот вектор перпендикулярен плоскости падения (т.е. параллелен оси Оy) то, как легко видеть, все векторы . Если этот вектор перпендикулярен плоскости падения (т.е. параллелен оси Оy) то, как легко видеть, все векторы 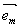 параллельны друг другу, и мы имеем параллельны друг другу, и мы имеем 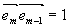 . .
Если же направление вектора 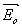 не составляет прямого угла с плоскостью падения, то не составляет прямого угла с плоскостью падения, то 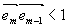 . Таким образом, поворот вектора . Таким образом, поворот вектора 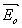 от положения, параллельного оси oy, приводит к уменьшению вклада от слагаемого, ответственного за связь между волнами. Мы будем рассматривать только практически наиболее важный случай максимальной связи и положим от положения, параллельного оси oy, приводит к уменьшению вклада от слагаемого, ответственного за связь между волнами. Мы будем рассматривать только практически наиболее важный случай максимальной связи и положим 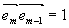 . .
Коэффициенты системы уравнений принимают более простой вид, когда направление исходной (восстанавливающей) волны, т.е. волны, падающей на решетку при дифракции, точно совпадает с направлением опорной волны при записи. Уравнения тогда будут:
- 31 -
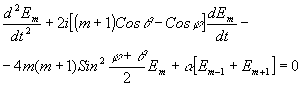
3. Исследование системы. Точное решение.
Независимо от направления исходной волны систему уравнений, описывающую дифракцию, можно представить в виде
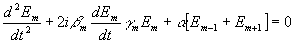
Вид этой системы таков, что ее можно интерпретировать как систему уравнений, описывающую колебательные процессы в системе связанных резонаторов. Назовем их квазирезонаторами.
Кроме этой системы, можно написать также и систему для сопряженных величин:
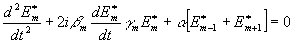
Граничные условия для решения задача должны быть выбраны, исходя из предположения, что при отсутствии связи (a
=0) никакой дифракции не будет, амплитуда колебаний всех квазирезонаторов, кроме Е0, а их производные равны нулю, а для Е0 имеется только постоянная составляющая. Амплитуда этой постоянной составляющей равна амплитуде исходной волны (мы принимаем ее равной единице). Таким образом, имеем
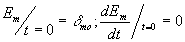
где
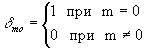
Дифрагировавшие волны возникают только благодаря связи волн
- 32 -
между собой. Поэтому граничный условия при a
¹
0 не должны отличаться от только что указанных.
Рассмотрим законы сохранения. Система уравнений для связанных волн em. имеет два интеграла, которые можно получить следующим образом. Умножим системы для em и e*m, на сопряженные величины, просуммируем по всем m и вычтем одну сумму из другой. Получим
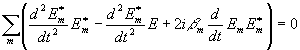
Вследствие того, что решением системы уравнений с постоянными коэффициентами является экспоненциальная функция , первые два члена полученного соотношения взаимно компенсируют друг друга и мы имеем
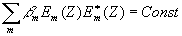
это первый закон сохранения в системе связанных квазирезонаторов.
Полученное выражение, как нетрудно видеть, представляет собой поток энергии, проходящий через поверхность, перпендикулярную оси z, расположенную в произвольном месте внутри среды. Сохраняется при дифракции, таким образом, не величина энергии вообще, а ее поток в направлении оси z и возможно "расплывание" энергии в направлении оси x, т.е. переход ее в высшие порядки дифракции.
В соответствии с этим законом дифракционную эффективность толстослойной голограммы нужно определять как отношение потока энергии в первом порядке дифракции к потоку энергии, падающему на поверхность решетки.
Из граничных условий следует, что
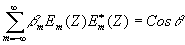
Для того, чтобы получить другой интеграл системы уравнений, умножим систему для e*m на 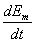 и, соответственно, систему для em на и, соответственно, систему для em на 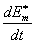 . После суммирования и сложения двух систем, аналогично предыдущему, получим . После суммирования и сложения двух систем, аналогично предыдущему, получим
- 33 -
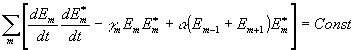
Это второй закон сохранения энергии в системе связанных квазирезонаторов. Первое слагаемое в выражении для второго закона 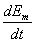 × ×
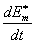 можно интерпретировать как кинетическую энергию, а слагаемое - g
m× можно интерпретировать как кинетическую энергию, а слагаемое - g
m×
e m×
e *m - как потенциальную энергию, а слагаемое a
(em-1+em+1)×
e*m – как энергию связи.
Свойства рассматриваемой системы квазирезонаторов, как видим, существенно отличаются от свойств системы обычных резонаторов. В системе квазирезонаторов, которым подобны связанные дифрагирующие волны, имеется два вида потенциальной энергии
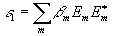
и 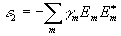
Из граничных условий следует, что
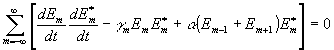
Отсюда можно сделать вывод, что скорость перехода энергия в различные порядки дифракции зависит от коэффициента связи a
и константы g
m.
Сходимость рядов, выражающих первый и второй законы сохранения, следует из теоремы существования и единственности решения системы дифференциальных уравнений. Из сходимости этих рядов следует, что em®
0 при m®
±
¥
. Таким образом, главную роль при дифракции играет волны нулевого и первых порядков. Нетрудно видеть, однако, что при совпадении восстанавливающего и опорного пучков кучей имеем g
о=g
-1=0 и энергия e
2 для этих порядков не существует. Поэтому потенциальная энергия e
2, накапливаясь в высших порядках, играет в системе роль сдерживающего фактора, затрудняя переход энергии к высшим порядкам дифракции.
Переход энергии в процессе дифракция осуществляется от волны нулевого порядка Е0 (которая одна только и существует в среде непосредственно после пересечения светом границы раздела), к волнам
- 34 -
высших порядков. В системе связанных резонаторов способность передачи энергии от одного резонатора к другому зависит от синхронизма колебаний на парциальных частотах, т.е. частотах, которые совершает одиночные резонатору, разделяющиеся при отсутствии связи на отдельные парциальные системы.
Найдем парциальные частоты. Положив коэффициент связи a
равным нулю, получим систему уравнении :
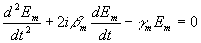
описывающую колебания не связанных друг с другом квазирезонаторов.
Каждый квази-резонатор, описываемый одним из уравнений системы, имеет (в отличие от обычных резонаторов) две различные по величине парциальные частоты:
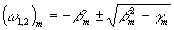
Колебания соответствующей квази-резонатору парциальной системы не будут гармоническими, так как отношение двух парциальных частот (w
1/w
2)m не является рациональным числом.
Выпишем значения парциальных частот для нескольких квазирезонаторов, близких к Е 0 (при совпадении восстанавливающего луча с опорным)
|
e2 |

|
|
e1 |
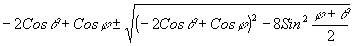
|
|
e0 |
0 ; cosq
|
|
e-1 |
0 ; cosj
|
|
e-2 |
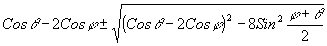
|
- 35 -
Рассмотрение величин парциальных частот показывает, что наиболее благоприятны условия для обмена энергией между нулевым и минус первым квазирезонаторами. Однако, если углы q
и j
малы, то парциальные частоты всех квазирезонаторов близки к нулю и, следовательно, с уменьшением углов q
и j
условия для распределения энергии по волнам различных порядков улучшаются. Наоборот, если углы q
и j
увеличивать, то энергия будет переходить, в основном, от волны кулевого порядка к волне минус первого порядка. Именно это условие и необходимо для получения большого значения дифракционной эффективности. Таким образом, одним из условий получения большого значения дифракционной эффективности является достаточная величина углов q
и j
. Знание парциальных частот, однако, дает возможность получить только качественную картину распределения энергии по порядкам дифракции.
Перейдем к системе уравнений при Наличии связи
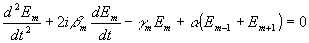
Ее собственные частота являются корнями характеристического уравнения
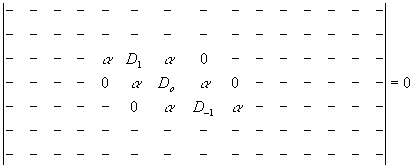
где dm =(w
2+2w
b
m+g
m), а общее решение имеет вид:
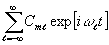
Коэффициенту cmℓ находятся из упомянутых выше граничных условий. Полное решение - сумма всех дифрагировавших волн – имеет теперь вид:
- 36 -
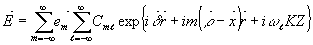
Как видно из этого решения, имеется два ряда дифрагировавших волн. Первый ряд представляет собой группу отдельных каналов, в каждом из которых распространяется также группа волн. Таким образом, каждая волна m-го порядка em(z) состоит, в свою очередь, из ряда (вообще говоря, бесконечного) близко расположенных волн. Эти вторые ряды волн представлены на рис.3. Для ясности рисунка углы между волнами сделаны много большими, чем это имеет место в действительности, а число волн ограничено четырьмя. Распространяясь почти в одном направлении, эти волны интерферируют, в результате чего интенсивность дифрагировавших волн при распространении их внутри среда изменяется по сложному закону.

Рис.3. Ряды волн распространяющихся в направлении одного дифракционного порядка.
- 37 -
Собственные частоты w
ℓ квазирезонаторов не являются кратными, и колебание всей системы не может быть разложено на ряд гармонических колебаний. Функции em(z) становятся суммами периодических функций с некратными периодами, т.е. представляют собой почти периодические функции переменной z, представленные обоими рядами Фурье. Теория таких функций и операций над ними хорошо разработана. Согласно этой теории, сумма колебании вида cmℓ×
exp[iw
ℓt] (которые по терминологии Г.Бора принято называть "чистыми") может быть объединена в ряд (ряд Фурье почти периодической функции). Сходимость ряда Фурье для функции em(z) следует из теоремы существования и единственности решения системы дифференциальных уравнений.
По теореме аппроксимации почти периодических функций функции em(z) могут быть аппроксимированы конечным рядом, составленным из чистых колебаний вида cmℓ×
exp[iw
ℓt] (в теории почти периодических функций доказывается сходимость рядов, расположенных по возрастающим величинам показателей w
ℓ).
Бесконечный характеристический детерминант, приведенный выше, может быть сделан абсолютно сходящемся с помощью деления каждой его строки на – (w
2+2w
b
m+g
m) Ограничиваясь числами mmax = m1, |
-mmax|
= m2, решая характеристическое уравнение, получим 2(m1+m2+1) собственных частот системы и представим таким образом, функции em(z) в виде 2(m1+m2+1) чистых колебаний. Таким путем можно получить решение системы уравнений для em(z) с любой заданной точностью.
В качестве примера приведем решение для следующих значений параметров: a
=0,1; u
=q
=j
=10°, волны порядка e0 и e-1 представлены в основном, двумя частота. Это дает основания для решения задачи в двухволновом приближении, что будет рассмотрено ниже.
На рис. 4 представлена зависимость интенсивностей |
em|
2 волн от переменной t = kz. Как видно из этого рисунка, интенсивность всех волн при распространении внутри среды испытывают сильные колебания. Интенсивности волн e0 и e-1 достигают максимума, близкого к единице, и уменьшаются до значений. близких к нулю. Максимальные значения интенсивностей других волн меньше. Из
- 38 -
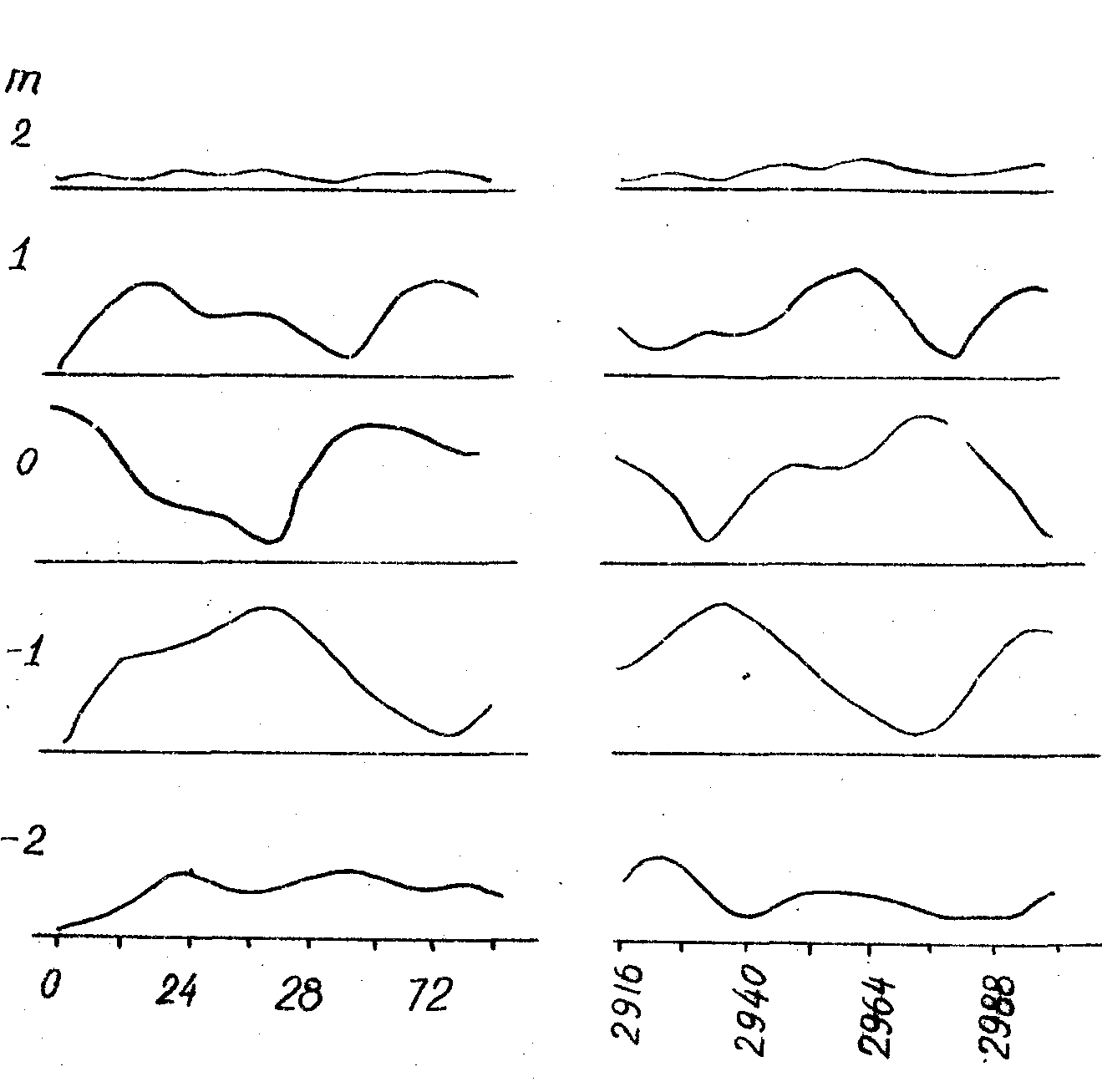
Рис .4. Колебания интенсивное света в порядках дифракции 2, 1, 0, -1, -2 при прохождении его через толщу среды для значений параметров
- 39 -
этого рисунка также видно, что волны с |
m|
³
3 не играют уже существенной роли и могут не приниматься во внимание.
Необходимо отметить, что в данной задаче не учтено отражение и преломление волн на границах с рады. Однако эти явления не имеют отношения к дифракции внутри среды, и не имеет смысла усложнять задачу, учитывая их. Необходимо лишь иметь в виду, что углы q
и j
- это углы, под которыми опорный и предметный пучки лучей распространяются внутри среды, но не вне ее.
4. Приближенные решения
С помощью ряда упрощающих предположений можно получить аналитические решения для двух предельных случаев дифракции, которые мы сейчас и рассмотрим. Предположим, что j
=q
(симметричное падение предметной и опорной волн на голограмму), и введем в уравнения малый параметр, для чего произведем замену переменной 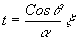 . Тогда система уравнений, описывавшая дифрагировавшие волны, будет . Тогда система уравнений, описывавшая дифрагировавшие волны, будет
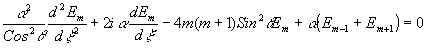
Если параметр 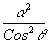 много меньше a
, то член со второй производной не будет играть заметной роли и его можно отбросить. Система уравнений значительно упрощается; много меньше a
, то член со второй производной не будет играть заметной роли и его можно отбросить. Система уравнений значительно упрощается;
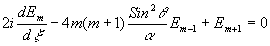
Дня исследования этой системы предположим вначале, что связь между волнами отсутствует (a
=0), и исследуем парциальные частоты. Получим систему уравнений:
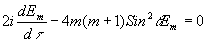
где
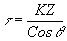
- 40 -
Эта система описывает колебания не связанных между собой квазирезонаторов (теперь уже гармонические). Каждый из резонаторов колеблется со своей парциальной частотой, кратной величине 4sin2q
.
Условием наилучшей передачи энергии от одного квазирезонатора к другому является, как известно, синхронизм колебаний парциальных систем, т.е. способность их колебаться в фазе длительное время. Будем считать, что колебания квазирезонаторов в достаточной степени синхронны, если на всем пути светового луча в среде фаза колебаний с частотой, равной парциальное, изменяется мало, т.е. величина набега фазы на толщине среды 4sin2q
×
t
/z=d, которую мы обозначим q, мала. При этом условии передача энергии от одного квазирезонатора к другому облегчена и интенсивности большого числа порядков дифракции (начиная с нулевого) будут мало отличаться друг от друга. Количественную оценку малости параметра q можно сделать на основе сравнения теории с экспериментом, такое сравнение, проводившееся многократно при изучении дифракции света на ультразвуке, показало, что возбуждение большого числа симметрично рассоложенных порядков дифракции наблюдается при значениях q порядка p
/12 и меньше. Отсюда имеем q£
p
/12 или, принимая во внимание, что q=4k×
d×
sinq
×
tgq
, получим
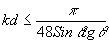
Область значений величины k×
d, удовлетворяющих этому неравенству, называется областью дифракции Рамана-Ната по имени исследователей, изучавших этот вид дифракции.
Если вернуться к упрощенной системе уравнений, описывающей колебания связанных квазирезонаторов,
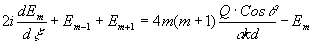
то, положив в ней, согласно сказанному, q=0, получим соотношение
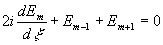
- 41 -
которому удовлетворяют функции Бесселя, если принять
em(x
) = im×
jm(x
)
Это и будет решением поставленной задачи в приближении Рамана-Ната.
Функции em(x
) удовлетворяют граничным условиям
em(0) = d
m0
в полном согласии с условиями постановки задачи.
Характер изменения амплитуд дифрагировавших волн указывает на то что в области дифракции Рамана-Ната происходит постепенная передача энергии от волны нулевого порядка симметрично ко всем волнам высших порядков при незначительном обратной возвращении к волне нулевого порядка. В результате такого процесса, если среда достаточно толстая, энергия в конце концов переходит к волнам высокого порядка и амплитуда волны нулевого порядка значительно уменьшится.
Такая картина однако является идеализированной и предполагает полный синхронизм колебаний парциальных систем. В действительности , с увеличением толщины среды (т.е. с увеличением d) синхронизм дифрагирующих волн все больше и больше нарушается, что затрудняет передачу энергии в высшие порядки дифракции.
Общим решением является сумма всех волн:
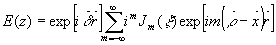
Ряд по функциям Бесселя легко суммируется, и мы получим волну
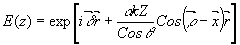
являющуюся исходной волной, модулирован ной по фазе.
Теперь легко видеть, что при дифракции в области Рамана-Ната происходит сдвиг только фазы исходной волны, пропорциональный распределению показателя преломления в среде.
Рассмотрим другой предельный случай, когда q велико. Синхронизма колебаний парциальных систем теперь не будет и передача энергии в высшие порядки дифракции, затруднится. Однако легко
- 42 -
видеть, что парциальные частоты квазирезонаторов Е0 и Е-1 равны нулю, в то время как парциальные частоты всех остальных квазирезонаторов теперь значительно отличаются от нуля. Это дает основания не рассматривать все уравнения системы, а ограничиться рассмотрением двух связанных квазирезонаторов, считая такую систему изолированной, т.е. предполагая, что энергия другим квазирезонаторам не передается.
Такая ситуация возникает в результате выполнения условия Брэгга ,
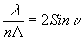
где L
- период дифракционной решетки, n - показатель преломления.
Период, решетки записанной с помощью двух плоских волн, как известно, равен
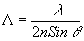
Если падавшая на решетку при дифракции волна точно совпадает с опорной, применявшейся при записи, то u
и условия Брэгга автоматически выполняются.
Мы имеем теперь систему уравнений в двухволновом приближении :
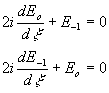
Эта система имеет не равные нулю собственные частоты 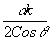 и и 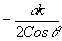 . Решением ее, при граничных условиях, приведенных раньше, будут гармонические колебания . Решением ее, при граничных условиях, приведенных раньше, будут гармонические колебания
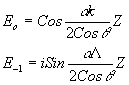
- 43 -
Интенсивности распространяющихся волн определятся выражениями
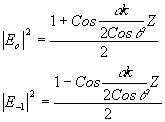
Необходимо выяснить, при каких величинах q можно считать две волны Е0 и Е-1 изолированными от других. Экспериментальные исследования показали, что это имеет место при q³
4p
или
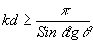
Область значений k×
d , удовлетворяющих этому неравенству, носит название области дифракции Брэгга. Область значений этого параметра, находящихся в пределах
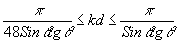
можно считать промежуточной областью.
Из выражений для интенсивностей дифрагирующих волн можно сделать вывод, что в области дифракции Брэгга происходит периодическая перекачка энергии из волны нулевого порядка в волну соседнего (минус первого) порядка и обратно. Процесс дифракции в этом случае аналогичен колебаниям системы двух связанных маятников, где при определенных начальных условиях энергия передается от одного маятника к другому подобным же образом.
Дифракцию в области Брэгга можно также рассматривать как результат "биений", получающихся при сложении двух волн, распространяющихся в каждом из двух каналов соответствующего порядка дифракции:
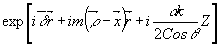
и
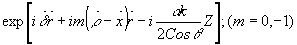
- 44 -
Из двух волн состоит как волна нулевого порядка Е0, так и волна минус первого порядка Е-1, так это представлено на рис.5. Сложение этих волн и приводит к биениям.
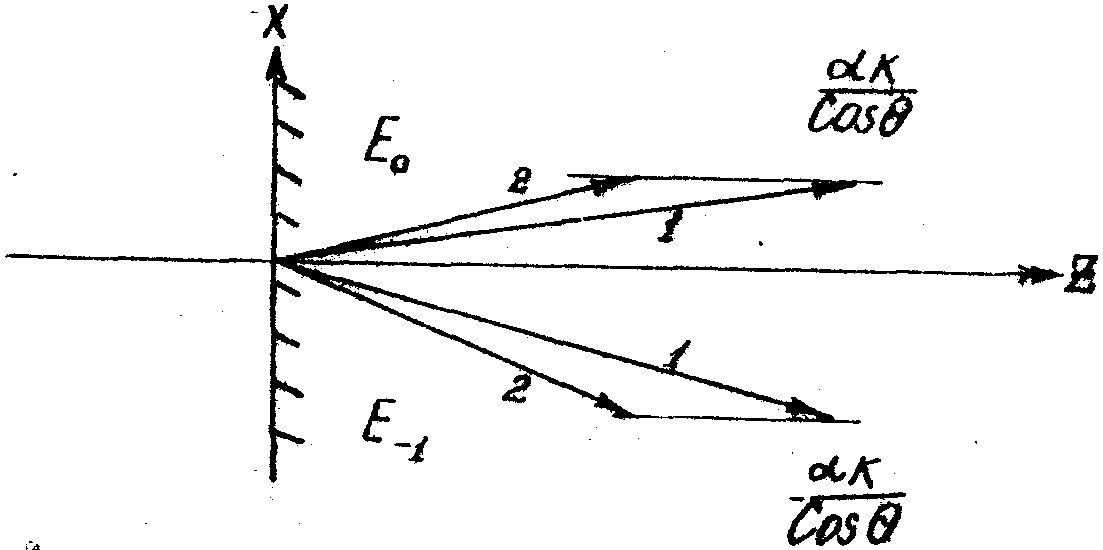
Рис.5. Пару волн, распространяющихся в нулевом и минус первом порядках при дифракции в области Брэгга.
Если условия Брэгга выполняются не точно (u
¹
0), то парциальная частота волны минус первого порядка несколько отличается от нуля, так что полного синхронизма волн нулевого и минус первого порядка не будет.
Колебания совокупности квазирезонаторов становятся негармоническими. Однако, при этом надо выделить случай, когда парциальная частота минус первого квазирезонатора гораздо ближе к нулю, чем парциальные частоты всех остальных. Тогда перекачка энергии осуществляется в основном опять между волнами нулевого и минус первого порядка. В этом случае очевидно, что u
и q
близки друг другу.
Приближения , которое мы здесь рассмотрели, дают правильную картину дифракции, только если коэффициент при второй производной a
2/cos 2q
много меньше коэффициента при первой производной a
, т.е. при соблюдении неравенства:
cos2q
>> a
- 45 -
Это неравенство всегда выполняется пря малых углах, и (так как a
не может быть больше 1/2). Однако при уменьшения угла q
величина q уменьшается и дифракция переходит из области Брэгга в промежуточную область. При больших углах q
рассмотренное приближение будет законно, только если a
очень мало.
Разделение дифракции в толстых слоях на три области иллюстрируется графиком рис.6, на котором представлена зависимость величины k×
d от угла q
. Как видно из этого рисунка, при изменении угла q
от 10 до 30 градусов толщина голограммы может быть уменьшена на порядок, но голограмма останется при этом толстослойной. Зависимостью свойств голограммы от угла q
можно объяснить возможность записи, на материале одной и той же толщины, голограмм, как со свойствами толстослойных, так и со свойствами тонкослойных, в зависимости от угла падения опорного пучка лучей.
При малых углах q
для получения толстослойных голограмм требуется весьма большая толщина слоя. При углах q
, близких к 90°, требуемая величина k×
d становится малой и в пределе (q
=90°) обращается в нуль. Это нетрудно понять из схемы падения лучей, представленной на рис.6. При падении луча на решетку под большим углом (как показано на рисунке пунктиром) путь света в среде значительно превышает толщину слоя, и поэтому размеры области, в которой происходит дифракция, значительно увеличиваются. Таким образом, одна толщина слоя еще недостаточна для характеристики голограмм. При разделении их на толстослойные и тонкослойные совершенно недостаточно сравнивать с длиной волны только толщину слоя, потому что на слое одной и той же толщины могут быть получены голограммы с различными свойствами.
Необходимо обратить внимание также и на то, что дифракция Брэгга не может быть практически наблюдаема при углах падения лучей, меньших 10°, и голограммы со свойствами толстослойных не могут быть при этом получены. Из рис.6 видно, что в области q
=8¸
10° кривая резко идет вверх так, что и при очень значительном увеличении толщины слоя для углов падения луча, например 10°, точка, изображающая величину k×
d, будет все время находиться в непосредственной близости от границы области Брэгга с промежуточной областью, где условия для возникновения этого вида дифракции неблагоприятны.
- 46 -
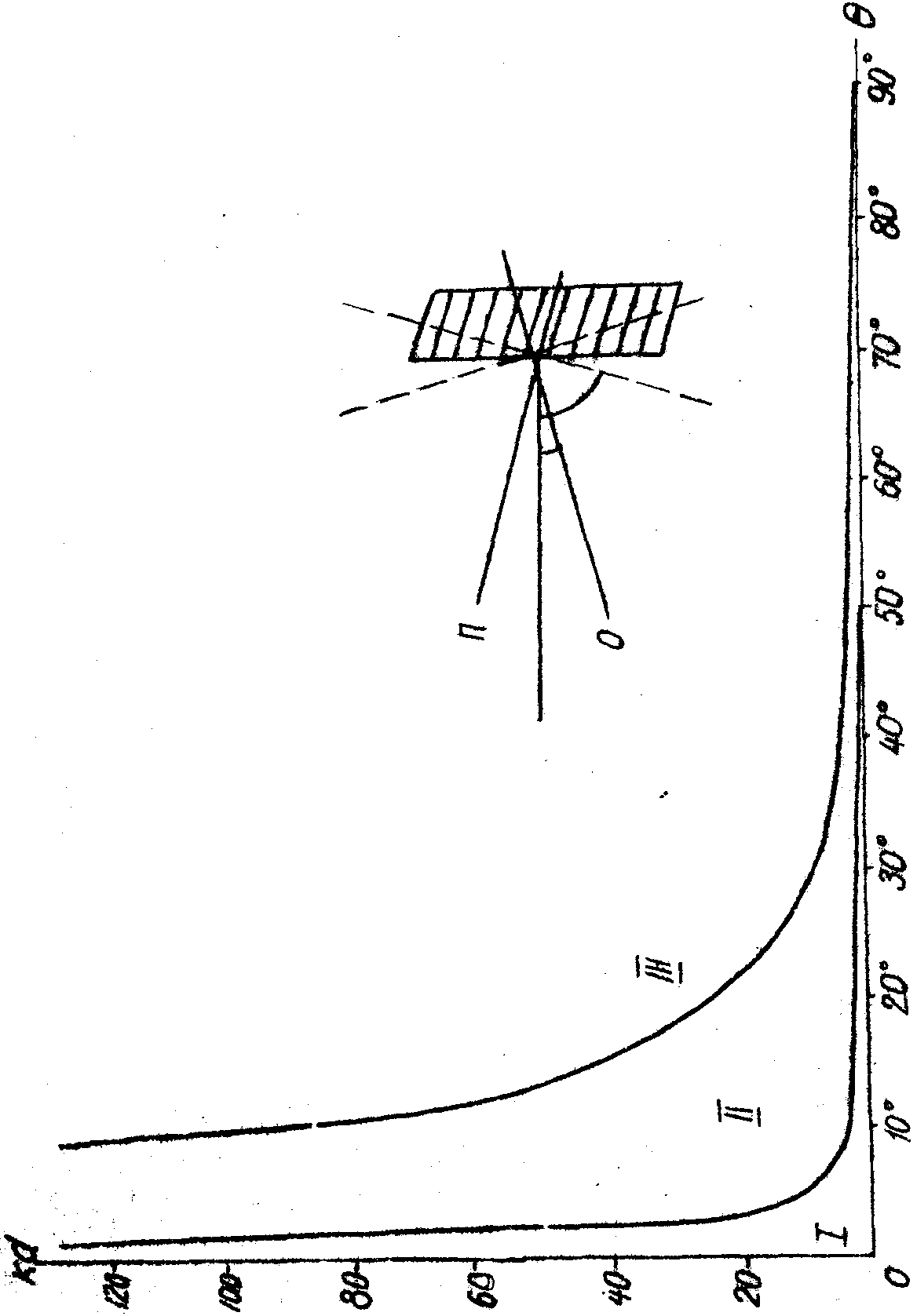
Рис.6. Области дифракции света в толстых слоях.
i – Область дифракции Рамана-Ната
ii – Промежуточная область.
iii – Область дифракции Брэгга.
- 47 -
То же демонстрируется графиками точного решения (рис.4), из которых видно, что при q
=10° возбуждаются соседние с нулевым и минус первым порядки даже для таких значений k×
d, для которых q, заведомо велико.
5. Диаграмма направленности толстослойной голограммы
Дифракционная решетка, рассмотренная выше, получена с помощью записи на голограмме одной составляющей разложения изображения голографируемого предмета по пространственным частотам. С ее помощью можно исследовать зависимость интенсивности излучения в любом порядке дифракции от угла падения на голограмму плоской волны, соответствующей заданной пространственной частоте /3/.
Проведя это исследование, мы получим зависимость дифракционной эффективности голограммы от пространственной частоты.
Дифракционная эффективность била выше определена как отношение энергии излучения в первом (минус первом) порядке дифракции к энергии излучения исходной волны. Из закона сохранения энергии, рассмотренного выше, было установлено, что сохраняющейся при дифракция величиной является поток энергии излучения через плоскость решетки, перпендикулярную оси z. Поэтому для определения дифракционной эффективности необходимо найти отношение соответствующих потоков энергии. В этом и состоит уточнение определения понятая "дифракционная эффективность" в случае толстослойных голограмм. С учетом того, что |
Е0|
2=1, будем иметь
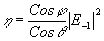
Предполагается, что восстанавливающая волна совпадает с опорной, т.е. u
=q
, и дифракция происходит в области Брэгга.
Для нахождения Е-1 при j
¹
q
нужно решить систему уравнений:
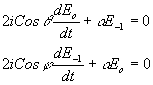
- 48 -
Собственными частотами этой системы будут 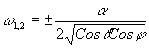 и решение при начальных условиях Е0 и решение при начальных условиях Е0(0)=1 , Е-1(0)=0 приводится к виду:
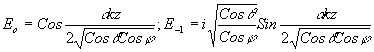
Дифракционная эффективность определится из приведенного выше выражения следующим образом:
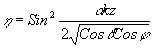
Дифракционная эффективность в рассматриваемом приближении будет, как то хорошо известно и как показывает порченное выражение, периодической функцией толщины слоя, изменяясь от 0 до 1. Период колебаний дифракционной эффективности зависит от величины связи a
и угла падения лучей на голограмму. При увеличении a
период колебаний дифракционной эффективности уменьшается так, что изменение a
в небольших пределах будет приводить к существенным изменениям дифракционной эффективности. С другой стороны, увеличение угла q
также приводит к уменьшению периода колебаний дифракционной эффективности и, следовательно, к тем же результатам.
Рассмотрение зависимости h
от угла j
дает возможность определить способность толстослойной голограммы к воспроизведению спектра пространственных частот. Толстослойные голограммы существенно отличаются этой способностью от тонкослойных. Для последних зависимости h
от угла j
нет.
Наглядно представить зависимость дифракционной эффективности от пространственной частоты можно, построив графики h
, как функции j
при различной величине z, которая теперь будет являться параметром. Набор величин z, для которых удобно строить графики, можно выбрать из условия, что при j
=q
для выбранной величины z должно быть h
=1. Этому условии удовлетворяют следующие значения аргумента: 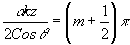 или или 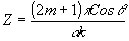 . .
- 49 -
где m=0,1,2... - число периодов "биений" двух волн, распространяющихся в одном канале.
Подставляя это значение z в выражение для h
, найдем
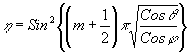
Из этого выражения следует, что наиболее выгодной величиной будет m=0.
На рис. 7 изображена диаграмма направленности в полярных координатах для m=0. Для построения графика принято значение в q
=30°. Если далее принять a
=0.01 и k=4×
104мм-1, то z будет иметь значения, соответственно, 1-6.5 мк, 2-65 мк, 3-270 мк.
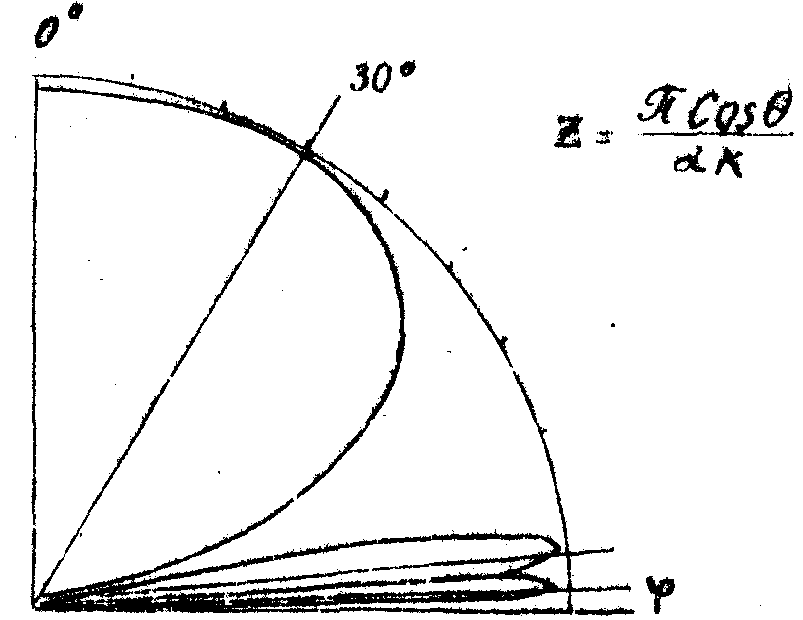
Рис. 7. Диаграмма направленности толстослойной голограммы в полярных координатах.
Увеличение толщины голограммы приводит к значительной неравномерности диаграммы направленности вследствие появления на ней "лепестков". Кроме того, при увеличении a
неравномерность диаграммы направленности появляется при все меньших и меньших толщинах слоя.
Как было уже сказано, зависимость дифракционной эффективности от пространственной частоты (диаграмма направленности ) не полностью характеризует толстослойную голограмму. Необходимо рассмотреть еще и фазовые соотношения между компонентами спектра пространственных частот. Однако легко видеть, что зависимости фазы от угла j
в нашем
- 50-
случае не будет. Выражение для Е-1 является чисто мнимым и, следовательно, фаза всех компонент спектра сдвинута на один и тот же угол.
В заключение отметим, что приведенные здесь графики диаграмм направленности являются идеализированными вследствие того, что мы использовали приближенные решения, законные лишь в случае a
<<cos2q
. Степень идеализации можно себе представить сравнивая в приближениями приведенные выше точные решения.
Литература
1. h.kogelnic. bell syst.tech.journ., 48, 9, 2909, 1969.
2. w.r.klein, b.d.cook. ieee. trans. on sonic and ultrasonic, v.su-14, 13, 123, 1967.
3. Н.М.Померанцев. В об. "Квантовая электроника" выл 5 (11) стр.118, 1972.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

