|
|
 |
 |

|
| |
ТРАНСФОРМАЦИОННЫЕ СВОЙСТВА ГОЛОГРАФИИ
А.Д.Гальперн
Проведено рассмотрение аберрационных искажений голограммы и описан метод построения гауссовского изображения.
Введение
Хорошо известно /1,2/, что изображение, создаваемое плоской голограммой, претерпевает различные трансформации вследствие перемещения реконструирующего источника, изменения масштаба голограммы и длины волны излучения, с помощью которого осуществляется восстановление. Под трансформациями изображения здесь понимается: его увеличение, изменение локализации в пространстве по сравнению о размерами и положением в пространстве объекта, а также аберрационные искажения изображения. Изучение вышеуказанных свойств голограммы представляет не только теоретический интерес, но крайне ваяно для таких, например, практических приложений голографии, как голографическая микроскопия и интроскопия в ультразвуковом или микроволновом диапазоне. Данная работа состоит из двух частей.
В первой части, освященной аберрациям голограммы, следуя работе /3/ будут получены выражения для направляющих косинусов лучей, идущих от голограммы в изображение. Затем будет дан метод расчета аберрационного рассеяния, основанный на использовании вышеуказанных выражений. После этого будут получены
- 6 -
формулы для лучевых аберраций изображения и установлена связь между лучевыми и волновыми аберрациями.
Во второй части работы будут выведены выражения для гауссовского изображения (т.е. изображения без учёта аберрационных искажений) и дан метод графического построения этого изображения.
1. Аберрационные искажения голографических изображений
Как известно /4/ голограмма представляет собой фотографическую запись интерференционной картины, создаваемой волновыми полями референтного источника и объекта:
y
r = arℓi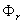
y
0 = a0ℓi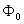
где y
r - волновая функция референтного источника, y
o - волновая функция объекта. На линейном участке характеристической кривой при коэффициенте контраста g
=-2 распределение амплитудного пропускания голограммы можно записать следующим образом:
t
= [|
y
o|
2+|
y
r|
2+y
oy
*r+y
o*y
r] (1)
При освещении проявленной голограммы восстанавливающей волной y
с=Асexp(iF
c) возникает поле, волновую функцию которого можно представить в следующем виде:
y
= y
с[|
y
o|
2+|
y
r|
2+y
oy
*r+y
o*y
r] (2)
Информацию об объекте содержат два последних члена выражения (2), из них третий соответствует истинному изображению, а четвёртый - сопряженному, и соответствии с (1) и (2) запишем выражения для фаз F
v и F
r истинного и сопряжённого изображений:
F
v = F
o+F
c-F
r
F
r = F
c-F
o+F
r (3)
- 7 -
при этом амплитуды ao, ar и ac мы считаем постоянными по всей поверхности голограммы. Для получения ощутимой амплитуды в какой-либо точке М пространства изображений необходимо, чтобы в этой точке пересекалось множество лучей, исходящих из какого-то конечного участка площади голограммы D
Х´
D
y. Найдём, каким условиям должны удовлетворять фазы в двух произвольных точках этого участка: m1(x,yo,0) и m2(x+D
x,yo,0) (рис.1). Длину луча mm1 обозначим через
rv(x,yo,0) , а длину луча mm2 - через rv(x+D
x,yo,0). Для того, чтобы колебания, попускаемые точками m1 и m2 складывались в точке М1, требуется выполнение следующего равенства:
F
v(x+D
x,yo,0)-F
v(x,yo,0) = 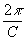 [rv(x+D
x,yo,0)- [rv(x+D
x,yo,0)-
-rv(x,yo,0)] (4)
Разделим обе части равенства (4) на D
Х и устремим m1 к m2; при этом D
x устремится к нуля и в пределе получим:
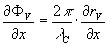 (5) (5)
где
rv = [(x-xv)2+(y-yv)2+zv2 (6)
xv,yv,zv - координаты точки изображения, x,y,0 - координаты произвольной точки голограммы.
Дифференцируя (6), получим, что 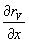 представляет собой направляющий косинус луча, идущего ив произвольной точки голограммы m в изображение: представляет собой направляющий косинус луча, идущего ив произвольной точки голограммы m в изображение:
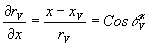 (7) (7)
Подставляя в (5) значении F
v из (3) и 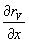 из (7), найдём: из (7), найдём:
- 8 -
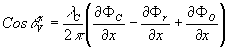 (8) (8)
В случае, когда объект, референтный и восстанавливающий источники являются точечными, выражения для F
c, F
r и F
v имеют следующий вид:
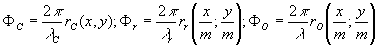 (9) (9)
где ro, rr, rc - расстояния от объекта референтного и восстанавливающего источников до точки с координатами, на голограмме; l
r и l
c - длина волны референтного и восстанавливающего источников; m - коэффициент масштабного преобразования голограммы. Подставляя (9) в (8), получим:
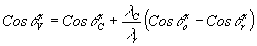 (10) (10)
где 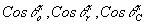 - косинусы углов, составленных осью x с лучами, идущими от объекта, референтного и восстанавливающего источников в данную точку голограммы. - косинусы углов, составленных осью x с лучами, идущими от объекта, референтного и восстанавливающего источников в данную точку голограммы.
Действуя аналогичным образом, найдём выражения для направляющих косинусов относительно оси y:
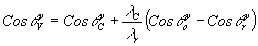 (11) (11)
Направляющий косинус относительно оси z легко найти из известного соотношения:
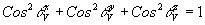 (12) (12)
- 9-
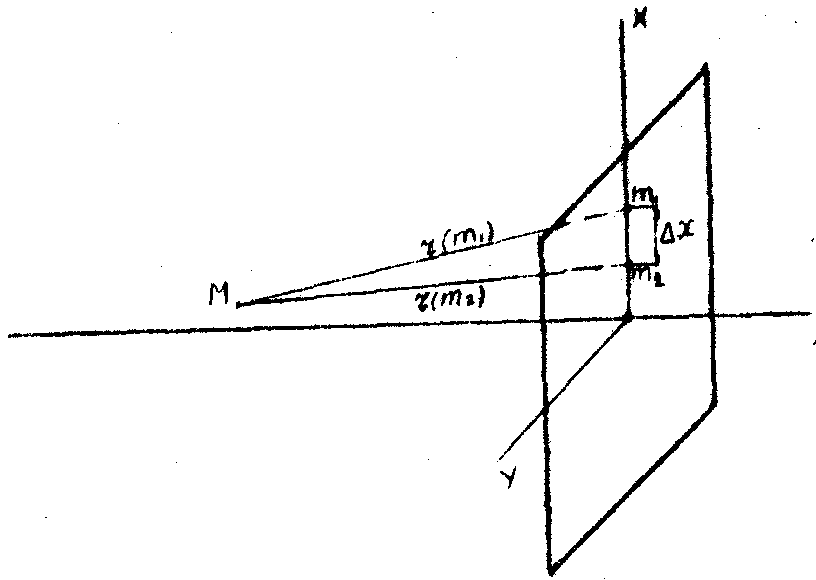
Рис.1.
Схема, поясняющая вывод формулы для направляющих косинусов лучей, идущих в изображение.
Для того, чтобы получить направляющие косинусы лучей, идущих в сопряжённое изображение, нужно изменить знак перед скобками в (10) и (11) на обратный *. Используя найденные выражения, можно определить величину аберрационного рассеяния в изображении. Для этого разобьём голограмму на n элементарных участков и будем считать, что каждый такой участок посылает в изображение только один луч. Определим плоскость наименьшей фигуры рассеяния, то есть плоскость, параллельную голограмме, в которой диаметр аберрационного кружка рассеяния минимален. Найдём координаты точек пересечения лучей, идущих от элементарных участков голограммы, с этой плоскостью. Диаметр круга, в котором будет укладываться порядка 90% всех точек пересечения, определим как меру аберрационного рассеяния голограммы.
Для определения плоскости наименьшего кружка рассеяния воспользуемся так называемой "функцией качества"; Эта функция может быть записана следующим образом:
* Выражения, аналогичные (10), (11), получены в работах /5,6/. В работе /5/ они выведены с помощью дифференциального интеграла Френеля-Кирхгофа и принципа стационарной фазы, а в работе /6/ на основе аналогии между голограммой и дифракционной решёткой.
- 10-
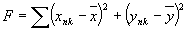 (13) (13)
Здесь
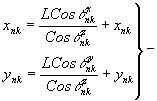 (14) (14)
координаты точки пересечения луча с произвольной плоскостью Н2, параллельной голограмме Н1 и находящегося на расстоянии l от неё (рис.2); xnk, ynk - координаты точки голограммы, находящейся внутри элементарного участка с номером n по оси x и с номером k по оси y, из которой исходит луч; 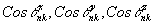 - направляющие косинусы этого луча; - направляющие косинусы этого луча; 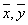 - координаты центра тяжести фигуры рассеяния в плоскости Н, они определяются следующим образом: - координаты центра тяжести фигуры рассеяния в плоскости Н, они определяются следующим образом:
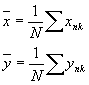 (15) (15)
Суммирование в (13) и (15) производится по всем элементарным участкам голограммы. Определим плоскость наименьшего кружка рассеяния Н как плоскость, параллельную голограмме, где функция f (13) принимает минимальное значение. Из этого определения следует, что для задания плоскости Н1 нам достаточно определить расстояние lu вдоль оси z, при котором функция f минимальна. Для нахождения lu необходимо решить относительно l следующее уравнение:
- 11 -
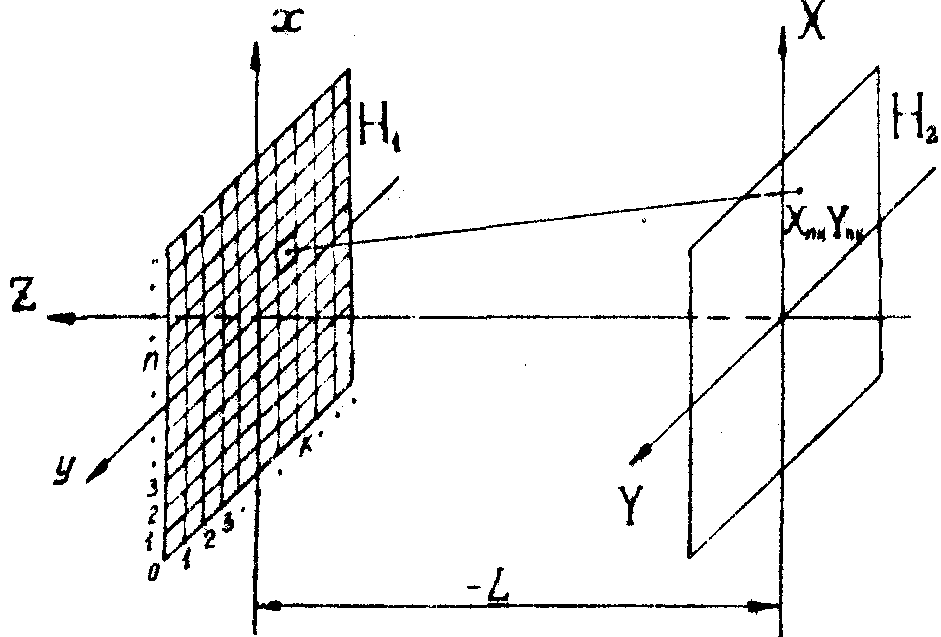
Рис. 2. Схема, поясняющая вывод уравнения плоскости наименьшего кружка рассеяния.
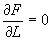 (16) (16)
а затем проверить минимально или максимально значение f при найденном l; если f - минимально, то найденное l= lu. Прежде чем решать (16), отметим, что если центр голограммы является началом координат, то справедливо следующее равенство:
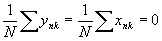 (17) (17)
Подставляя в (16) выражения (13)-(15) и учитывая (17), после довольно простых, но громоздких вычислений, решим (16) относительно l и тем самым найдём величину lu, при которой f экстремально:
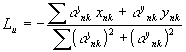 (18) (18)
- 12 -
где
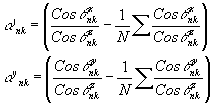
Нетрудно найти вторую производную от f по l, выражение для неё имеет вид:
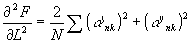 (19) (19)
Из (19) следует, что 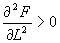 при любом l, следовательно, lu является значением l, при котором f минимально. Подставив lu в (14) и (15), найдём координаты точки пересечения лучей, идущих от голограммы, с плоскостью наименьшего кружка рассеяния. Зная координаты вышеуказанных точек, можно построить фигуру аберрационного рассеяния. Однако для большинства задач необходимо определить лишь диаметр фигуры. Этот диаметр может быть определён следующим образом: при любом l, следовательно, lu является значением l, при котором f минимально. Подставив lu в (14) и (15), найдём координаты точки пересечения лучей, идущих от голограммы, с плоскостью наименьшего кружка рассеяния. Зная координаты вышеуказанных точек, можно построить фигуру аберрационного рассеяния. Однако для большинства задач необходимо определить лишь диаметр фигуры. Этот диаметр может быть определён следующим образом:
r
£
r
t, 0 £
t £
m (20)
где
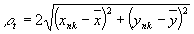 (21) (21)
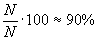 (22) (22)
Вышеописанная методика определения аберрационных искажений удобна при использовании электронно-вычислительных машин. Для оценок аберраций голограмм без использования счётно-решающей техники удобнее пользоваться аналитическими выражениями для волновых или лучевых аберраций через аберрационные коэффициенты.
- 13 -
Введём понятие лучевых аберраций.
Пусть Н1 и Н2 — плоскость голограммы и плоскость гауссовского изображения, соответственно (рис.3); Р1 - произвольная точка на голограмме с координатами Х,y; Р2 - точка пересечения луча, выходящего из Р1, с плоскостью гауссовского изображения - Н2. Если Рг - гауссовское изображение точки, восстановленное голограммой, то вектор 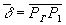 , согласно /7/, называется лучевой аберрацией. Найдём компоненты лучевой аберрации вдоль осей Х и y. Для этого необходимо определить координаты точки Р2 пересечения луча Р1Р2 с плоскостью Н2. Уравнение плоскости Н2 имеет вид: , согласно /7/, называется лучевой аберрацией. Найдём компоненты лучевой аберрации вдоль осей Х и y. Для этого необходимо определить координаты точки Р2 пересечения луча Р1Р2 с плоскостью Н2. Уравнение плоскости Н2 имеет вид:
z = -zG
(23)
где zG
- расстояние вдоль оси z между плоскостями Н1 и Н2. Уравнение прямой Р1Р2 запишем обычным образом:
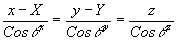 (24) (24)
Здесь Х ,y,z - текущие координаты прямой Р1Р2, а cosq
x, cosq
y, cosq
z - направляющие косинусы этой прямой.
Решая (23) и (24) совместно, находим координаты искомой точки пересечения Р2:
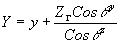 (25) (25)
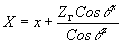 (25') (25')
Действуя аналогичным образом, нетрудно записать координаты гауссовского изображения xG
и yG
:
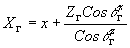 (26) (26)
- 14 -

Рис. 3. Схема, поясняющая вывод формуя для лучевой аберрации голограммы.
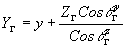 (26') (26')
Здесь 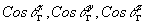 - направляющие косинусы прямой, идущей из точки Р1 голограммы в гауссовское изображение РG
. Используя (25) и (26), можно записать компоненты лучевой аберрации d
y и d
x следующим образом: - направляющие косинусы прямой, идущей из точки Р1 голограммы в гауссовское изображение РG
. Используя (25) и (26), можно записать компоненты лучевой аберрации d
y и d
x следующим образом:
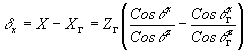 (27) (27)
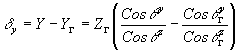 (27') (27')
Ясно, что лучевая аберрация 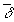 может быть выражена через d
x и d
y с помощью следующего выражения: может быть выражена через d
x и d
y с помощью следующего выражения:
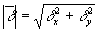 (28) (28)
- 15 -
Рассмотрим переход от лучевых аберраций к волновым. Согласно /7/, выражения (27) связаны с волновой аберрацией следующим соотношением:
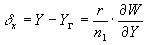 (29) (29)
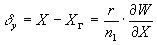 (29') (29')
Здесь r - модуль вектора Р1p 2, - показатель преломления среды, в которой происходит распространение лучей (в нашем случае n=1).
Из (29) и (29')следует, что выражение для волновой аберрации через лучевые имеет вид:
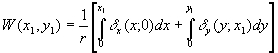 (30) (30)
Подставляя в (30) выражений (27), (27') и пользуясь тем, что
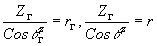
перепишем (30) следующим образом:
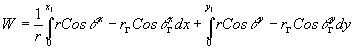 (31) (31)
Для большинства практических приложений r в выражении (31) может быть заменено на rГ. Используя это обстоятельство, а также выражения (5)-(10), получим, что волновая аберрация голограммы может быть записана в следующем виде:
w = F
С±
(F
о-F
r)-F
Г (32)
где F
Г - распределение фазы поля, распространяющегося от гауссовского изображения в плоскости голограммы.
Полученная нами формула (32) полностью совпадает с выражением для волновой аберрации, данный в работе /2/.
В данной работе нам хотелось показать связь лучевых и волновых аберраций, а также отметить, что точность, с которой волновая аберрация записывается с помощью (32), ограничивается предположением
- 16 -
положением о равенстве r и rГ в выражении (31). Мы не будем останавливаться здесь на аналитической записи волновой аберрации через аберрационные коэффициенты, так как это достаточно подробно и хорошо сделано в работах /2,8/.
2. Гауссовское изображение
В тех случаях, когда нас не интересуют аберрационные искажения изображения и необходимо определить лишь его локализацию и увеличение, достаточно рассматривать только гауссовское изображение. Законы, описывающие это изображение, довольно просты, так как при их выводе используется предположение о малости углов падения на голограмму лучей от объекта, референтного и восстанавливающего источников. Используя данное предположение, а также выражения (10), (11), найдём формулы, связывающие утлы падения на голограмму лучей, идущих от гауссовского изображения, с углами падения лучей, идущих от объекта, референтного и восстанавливающего источников. Для этого заменим в (10), (11) косинусы на синусы дополнительных углов. Выразим синусы через тангенсы. Так как дополнительные углы достаточно малы, оставим только первые степени тангенсов и в результате получим следующие выражения:
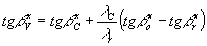 (34) (34)
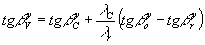 (34') (34')
где 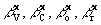 - углы, дополнительные - углы, дополнительные 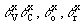 ; аналогичные обозначения введены для углов относительно оси y. В данном приближении тангенсы вышеуказанных углов равны тангенсам углов, составленных проекциями на плоскости xoz и yoz лучей, идущих от изображения, объекта, референтного и восстанавливающего источников к голограмме. Пользуясь формулами (34) и (34'), нетрудно определить координаты гауссовского изображения. ; аналогичные обозначения введены для углов относительно оси y. В данном приближении тангенсы вышеуказанных углов равны тангенсам углов, составленных проекциями на плоскости xoz и yoz лучей, идущих от изображения, объекта, референтного и восстанавливающего источников к голограмме. Пользуясь формулами (34) и (34'), нетрудно определить координаты гауссовского изображения.
- 17 -
Для этого выберем на голограмме две точки m1(x1;y;0) и m2(x1+D
x;y;0) и построим лучи, идущие из этих точек в гауссовское изображение. Уравнение проекций этих лучей па плоскость xoz можно записать в следующем виде:
x-x1 = tgb
xv×
z
x-(x1+D
x) = tgb
1v×
z (35)
Решая систему (35) и используя при атом (34), находим:
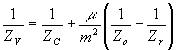 (36) (36)
Здесь zv, zo, zc, zr - координаты изображения, объекта, референтного и восстанавливающего источников вдоль оси z; m - коэффициент масштабного преобразования голограммы; 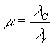 - отношение длин волн излучения. Пользуясь (35) и (36), можно определить xv координату гауссовского изображения вдоль оси x: - отношение длин волн излучения. Пользуясь (35) и (36), можно определить xv координату гауссовского изображения вдоль оси x:
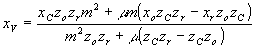 (37) (37)
Здесь x0, xr xc - координаты объекта, референтного и восстанавливающего источников вдоль оси x.
Координату гауссовского изображения yv относительно оси y можно определить, составляя систему уравнений, подобную (35), но уже в плоскости yoz, и пользуясь выражением (34'):
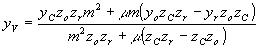 (37) (37)
Используя выражения (36) - (38), можно определить локализацию истинного гауссовского изображения; для определения локализации сопряжённого изображения достаточно поменять в (36) - (38) знак перед всеми скобками на обратный. Кроме того, следует отметить, что при помощи вышеуказанных выражений можно определить как продольное, так и поперечное увеличение изображения. Мы не будем останавливаться здесь на выводе формул для
- 18 -
вышеуказанных увеличении, так как их подробный вывод дан в работе /2/, отметим только, что как формулы (36)-(38), так и формулы для увеличения изображения достаточно громоздки и неудобны в обращении. В связи с этим остановимся на рассмотрении довольно простого графического метода построения гауссовского изображения, предложенного в работе /9/. Вначале проведём построение истинного изображения для случая, когда m
=m=1. Построим плоскость l, параллельную голограмме на произвольном расстоянии К от неё (рис.4). Лучи, проведённые из начала координат к объекту, изображению, референтному и восстанавливающему источникам, пересекаются с плоскостью l в точках, координаты которых обозначим через x'oy'o; x'vy'v; x'ry'r; x'cy'c; очевидно, что последние будут пропорциональны тангенсам углов 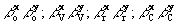 . .
Подставляя в (34) и (34*) значения тангенсов, выраженные через x'oy'o; x'vy'v; x'ry'r; x'cy'c, и затем сокращая правую и левую части полученных выражений на коэффициент пропорциональности, получим:
x'v = x'c+(x'o-x'r) (39)
y'v = y'c+(y'o-y'r) (39')
Перенося в левую часть формулы (39), (39') величины, относящиеся к записи голограммы, а в правую - к реконструкции, найдём:
x'o-x'r = x'v-x'c (40)
y'o-y'r = y'v-y'c (40')
Левая часть уравнений (40), (40') характеризует конфигурацию системы: референтный источник, объект так, как её видно из начала координат, правая - конфигурацию системы: восстановленное изображение, реконструирующий источник. Из (40), (40') следует, что введённая таким образом характеристика (которая геометрически представляется как система точек, в которых лучи, идущие из
- 19 -
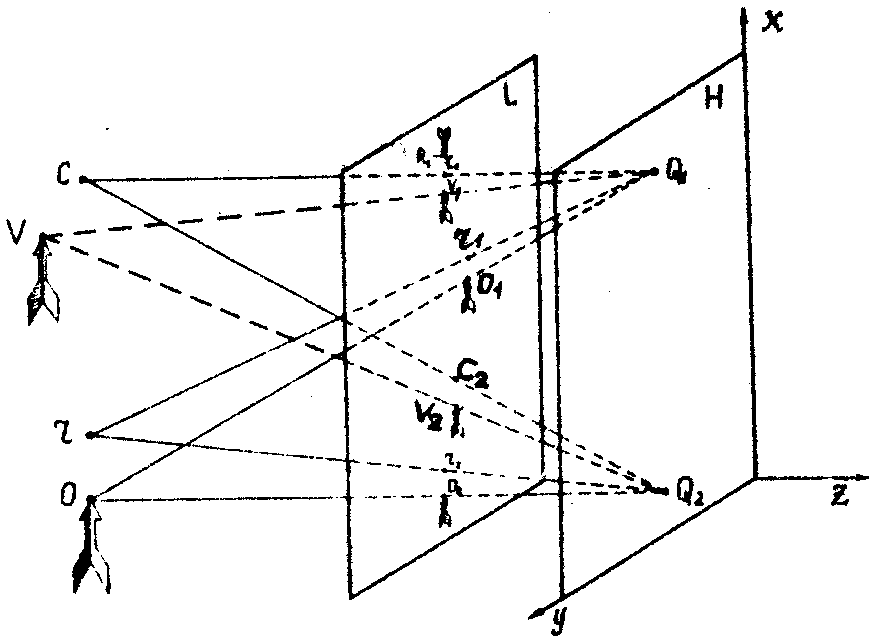
Рис.4. Схема построения изображения объекта:
О - объект, r - референтный источник, С - восстанавливающий источник, v - истинное изображение, Н - плоскость голограммы, q1, q2 - точки наблюдения на голограмме, l - вспомогательная плоскость.
данной точки голограммы в точки объекта, пересекают плоскость l) инвариантна при любых трансформациях восстановленного изображения, происходящего за счёт перемещения реконструирующего источника. Назовём эту характеристику "следом".
Поскольку начало координат было выбрано произвольно, след можно определить для любой точки голограммы. Из вышеизложенного непосредственно следует весьма простой способ графического построения восстановленного изображения. Проведём из двух произвольных точек голограммы q1 и q2 лучи к референтному источнику r и к интересующим нас точкам объекта (чтобы не загромождать чертёж, на рисунке выделена только одна точка объекта o). На пересечении этих лучей с плоскостью l получим две системы точек (r1o1 и r2o2 на рис.4), каждую из которых можно рассматривать как графическое представление следа объекта для данной точки голограммы. Перейдём к процессу восстановления.
- 20 -
Пусть реконструирующий источник находится в точке С . Лучи, соединяющие этот источник с точками q1 и q2, пересекут плоскость l в точках С1 и С2.
Из выражений (40), (41') следует, что точки пересечения лучей, идущих из q1 и q2 в точки изображения, с плоскостью (точки v1 и v2 на рис.4) располагаются относительно точек С1 и С2 так же, как точки О1 и О2 пересечения соответствующих лучей, идущих к объекту, располагаются относительно точек r1 и r2. Используя введённую ранее терминологию, можно сказать, что след смещается, не деформируясь, вместе с точкой пересечения луча, который соединяет источник излучения и данную точку голограммы.
Найдя таким образом новые положения следов, проведём через их идентичные точки v1 и v2 лучи q1v1 и q2v2. Точка пересечения этих лучей определит положение точки истинного изображения v.
Рассмотрим построение сопряжённого изображения. Для сопряжённого изображения все предыдущие рассуждения полностью аналогичны, необходимо только заменить в выражениях (39), (39') знак перед скобками на обратный, тогда можно записать следующие выражения:
x'o-x'r = -(x'r-x'c) (41)
y'o-y'r = -(y'r-y'c) (41')
Из (41), (41') следует, что точки r1 пересечения с плоскостью l лучей, идущих из q1 в точки сопряжённого изображения, располагаются центрально-симметрично относительно точки С1 к точкам пересечения лучей, проведённых в истинное изображение из точки q1; короче говоря, след сопряжённого изображения центрально-симметричен относительно точка С1 следу истинного изображения.
Кратко остановимся на случае построения истинного изображения, когда m
¹
m¹
1. Очевидно, что выражения (40), (40') примут при этом следующий вид:
x'o-x'r = 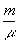 (x'r-x'c) (x'r-x'c) (42)
- 21 -
y'o-y'r = 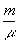 (y'r-y'c) (y'r-y'c) (42')
Из выражений (42), (42') следует, что в этом случае след объекта трансформируется с коэффициентом увеличения 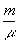 . Остальные построения как в этом случае, так и в случае сопряжённого изображения аналогично приведённым ранее. . Остальные построения как в этом случае, так и в случае сопряжённого изображения аналогично приведённым ранее.
В заключение отметим, что существуют и другие способы графического построения изображений, они рассмотрены в работах /3,10,11/.
Литература
1. e.n.leith, j.upatnieks, k.a.haines. josa, 55, 8, 981, 1965.
2. r.w.meier. josa, 55, 8, 987, 1965.
3. А.Д.Гальперн, Ю.Н.Денисюк. ОМП, № 10, стр. 29-32, 1969.
4. d.gabor. proc.roy.soc., a197, 454, 1949.
5. c.w.helstrom, josa, 56, 433, 1966.
6. a.offner. josa, 56, 1509, 1966.
7. М.Борн, Э.Вольф. Основы оптики, изд. "Наука", М., 1970.
8. e.b.champangne. josa, 57, n1, 860, 1967.
9. Ю.Н.Денисюк, А.Д.Гальперн. Жур. Оптика и спектроскопия, 27, стр.175, 1969.
10. А.В.Ковальский, В.К.Полянский, В.Б.Тимофеев. Квантовая электроника. Труды республиканского семинара, вып.5, "Наукова думка", Киев, стр.74, 1965.
11. А.Д.Гальперн, Ю.Н.Денисюк. Голография и её использование в оптике. Материалы семинара, ч.1. Лен. Дом научно-техн. пропаганды, Л., стр.24, 1970.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

