|
|
 |
 |

|
| |
РАЗРЕШАЮЩАЯ СПОСОБНОСТЬ И АБЕРРАЦИИ ГОЛОГРАММ
К.С.Мустафин
Рассмотрены факторы, определяющие пределы разрешения голограмм. Приведены расчётные и экспериментальные данные, удовлетворительно согласующиеся между собой.
Перспективы применения голографии в ряде областей (в микроскопии, в хранении информации, в технологии изготовления микросхем и др.) существенно зависят от разрешающей способности, которая может быть достигнута в изображениях, восстанавливаемых с помощью голограмм. Поэтому весьма важно знание факторов, ограничивающих разрешающую способность голограмм и умение свести их на практике до минимума. К таким факторам относятся: стационарность условий при голографировании, частотно-контрастная характеристика фотоматериала, степень когерентности источника излучения и аберрации голограмм.
Не имен возможности подробно останавливаться на всех указанных выше факторах, ограничимся на некоторых кратким упоминанием.
При записи голограмм весьма жесткие требования предъявляются к стационарности условий: отдельные элементы установки в течение времени экспонирования не должны смещаться друг относительно друга более чем λ/8. (где λ - длина волны при голографировании). Допустимые смещения объекта при голографировании в отражённом свете также не более λ/8 , а при голографировании в проходящем свете - не более d/8, где d- наименьший размер объекта, который требуется разрешить при восстановлении.
Влияние частотно-контрастной характеристики фотоматериала выражается в ограничении эффективной апертуры или высоких про-
странственных частот при голографировании. С целью уменьшения этого эффекта в голографии используют высокоразрешающие фотоматериалы.
Этими краткими сведениями ограничимся в отношении первых двух упомянутых выше факторов.
i. Влияние степени когерентности источника в голографии
а) Влияние временной когерентности
В общем случае временная когерентность определяет глубину голографируемой сцены, а пространственная когерентность - ширину её. Однако, даже при голографировании плоских объектов (транспарантов), ограниченная временная когерентность источника влияет на качество изображения. Оно выражается в ограничении эффективной апертуры голограммы и, следовательно, её разрешающей способности.
Связь между аффективным диаметром голограммы dэф и шириной линии излучения Δ λ μожно найти элементарным геометрическим рассмотрением задачи. При этом для случая голографирования по двухосевой схеме можно написать:
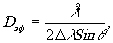 (1) (1)
где θ- угол голографирования. К такому же результату приводит и более строгое рассмотрение задачи /1/.
Для случая одноосевой (габоровской) голографии такое же простое геометрическое рассмотрение приводит к следующему выражению:
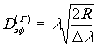 (2) (2)
где Я - расстояние от голографируемого объекта до голограммы. Анализ ( 1) и (2) показывает, что требование к временной когерентности в случае одноосевой (габоровской) голографии более умеренное, чем в случае двухосевой (лейтовской) голографии. На-
пример, при λ = 5·10-5 cм, θ = 30°, r = 10 см одноосевая голограмма, снятая при ΔλГ = 0,8 Å даёт такое же разрешение, что и двухосевая голограмма при Δλ= 0,1 Å. В данном случае выигрыш в длине когерентности в 8 раз.
б) Влияние пространственной когерентности /2/
Этот случай практически более интересен. Влияние пространственной когерентности источника излучения также выражается в ограничении эффективной апертуры голограммы и, следовательно, её разрешающей способности.
Пространственная когерентность поля излучения зависит от протяжённости источника и расстояния, т.е. определяется угловыми размерами источника и характеризуется функцией
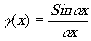 , (3) , (3)
где 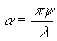 , ,
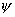 -
угловой размер источника, х- координата. -
угловой размер источника, х- координата.
Предположим, что методом Фурье-голографии производится голографирование точечного объекта с помощью протяжённого источника (рис.1).
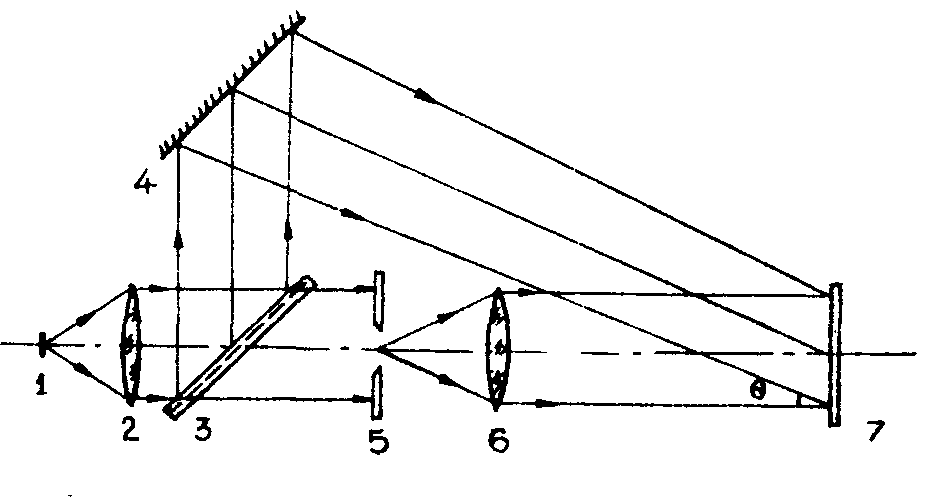
Рис.1 Схема получения Фурье-голограмм:
1 - протяжённый источник света; 2,6 - линзы, 3 - делительная тастинка; 4 - зеркало; 5 - диафрагма, 7 - голограмма.
Распределение интенсивности на голограмме 7 при единичной амплитуде будет:
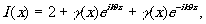
где θ - угол голографирования, 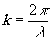 . При реконструкции за голограммой в первом порядке дифракции будет восстановлена
волна с амплитудой
. При реконструкции за голограммой в первом порядке дифракции будет восстановлена
волна с амплитудой
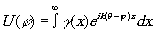 (4) (4)
С помощью (4), с учётом (3), можно найти среднее квадратичное отклонение 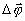 угла дифракции φ:
угла дифракции φ:
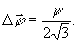
Зная угловое размытие 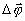 ,
легко определить эффективный диаметр голограммы dэф ,
легко определить эффективный диаметр голограммы dэф,
обусловленный протяжённостью источника:
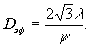
Исследования показывают, что приведённые выше выражения для разревавщей способности голограмм в зависимости от степени когерентности удовлетворительно согласуются с экспериментальными данными /3/. При неограниченной разрешающей способности регистрирующей среды и высокой степени когерентности источника голограммы позволяют достичь дифракционного предела разрешения, обусловденного их размерами /4,5/.
2. Аберрации голограммы
Голограммы так же, как и обычные оптические системы, не свободны от аберраций, которые могут существенно влиять на качество изображения. Поэтому учёт аберрационного состояния голографического изображения весьма важен с точки зрения практического достижения высокого разрешения.
Изучению аберраций в голографии посвящён ряд работ /6-13/. Работы /6-8/ посвящены теории аберраций третьего порядка в голографической микроскопии. В работе /9/ даётся обобщение работ /6-8/ на случай непараксиальных лучей. В работе /l0/ рассмотрены разрешающая способность в голографии, а также вопросы аберрации и приведены некоторые экспериментальные данные. И работе /11/ рассыатривается влияние на качество изображения аберраций, имеющих порядок выше третьего. Работа /12/ посвящена анализа аберраций третьего порядка в Фурье-голографии. В работе /13/ приводится анализ аберрационного состояния в голографической интерферометрии при использовании высших порядков дифракции.
Ниже будут рассмотрены, на основе теоретических и экспериментальных данных по аберрациям голограмы, те факторы, с которыми приходится считаться при получении голографических изображений с высоким разрешением. Такое рассмотрение даёт возможность правильно оценить требования к голографической технике и пределы поля высокого разрешения. Последнее, в свою очередь, важно с точки зрения размножения изображения в технологии изготовления интегральных схем.
а) Геометрические соотношения между объектом и его изображением
Геометрические соотношения между объектом и его изображением, а такие аберрации голограмм ыогут быть выведены из сравнения фронта волны точечного объекта, восстановленного с голограммы, с гауссовой референтной волной.
Рассмотрим фазу волны Ф 0(х;y) от точечного источника О(х0;y 0;z 0) в какой-либо точке Ρ(x,y) плоскости голограммы (рис.2):
Ф 0(x;y)=k r 0,
где 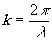 ,
λ - δлина волны излучения,
r0 -
расстояние от точки o(x0,y0,z0)
до точки p(х,y). ,
λ - δлина волны излучения,
r0 -
расстояние от точки o(x0,y0,z0)
до точки p(х,y).
Согласно обозначениям рис.2, можно написать:
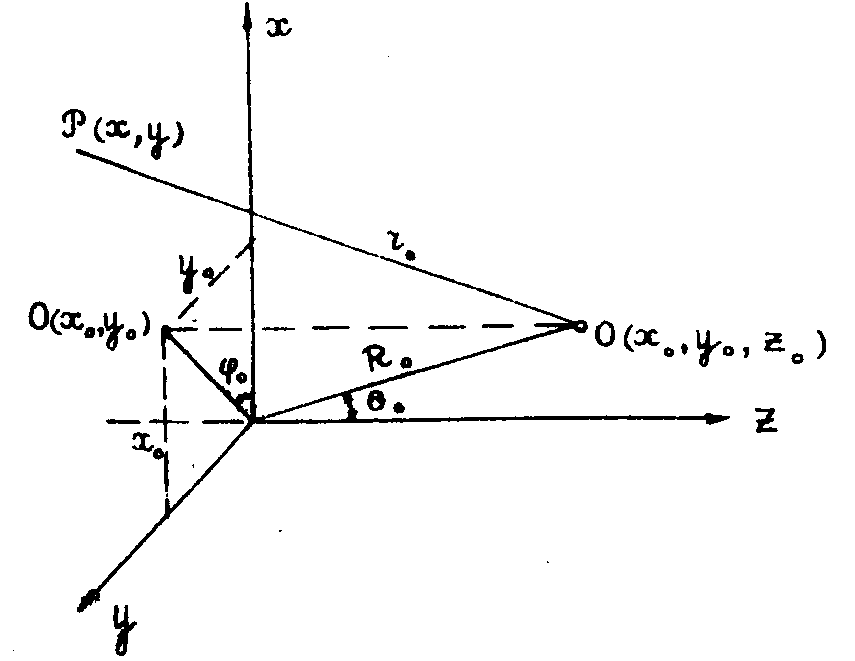
Рис.2. К расчёту фазы сферической волны на голограмме:
О(x 0,y 0,z 0) - точечный источник;
p(x,y) - текущая точка на голограмме;
θ - σ гол между радиусом-вектором точки О и осью z;
r0 - модуль радиуса-вектора точки;
r0 - расстояние между точечным источником О и текущей точкой Р(x,y);
φ 0 - угол между осью x и радиуcом-вектором проекции О(х0,y 0) точки o.
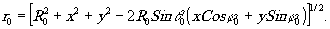 (5) (5)
Воспользуемся условием, что в каждый данный момент времени суммарная фаза волн, участвующих при голографировании и восстановлении (с учётом знаков) должна равняться нулю в каждой точке голограммы:
ru=rb ±μ(rc-r 0), (6)
где 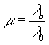 ,
λb
и λ0 ,
λb
и λ0 - длина
волны при восстановлении и голографировании, соответственно; значки u, b,
с, о - относятся к изображающей, восстанавливающей, сигнальной и опорной волнам,
соответственно. Величины r
определяются выражением типа (5). Подставляя значения r,
в первом приближении в (6) и приравнивая коэффициенты при одинаковых степенях
x и y
слева и справа, находим:
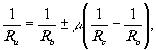 (7) (7)
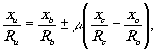 (8) (8)
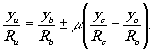 (9) (9)
Уравнение (7) связывает расстояния от голограммы до объекта и его изображения, а (8) и (9) - угловые соотношения между ними в зависимости от условий получения и восстановления изображения.
б) Аберрации голограмм третьего порядка
Аберрации третьего порядка можно определить при учёте третьего члена разложения в ряд в выражении (5). Этот член отдельно можно написать в виде:
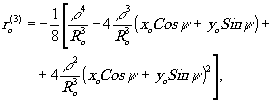 (10) (10)
где введены полярные координаты в плоскости голографии:
x=ρ cos ψ, y=ρ sin ψ ,
Величина отклонения фазы восстановленной волны от гауссовской волны (волновые аберрации третьего порядка) будет:
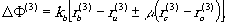 (11) (11)
где каждый 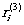 определяется выражением вида (10).
определяется выражением вида (10).
Подставляя в (11) развернутые значения 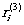 и произведя соответствующую группировку, получим:
и произведя соответствующую группировку, получим:
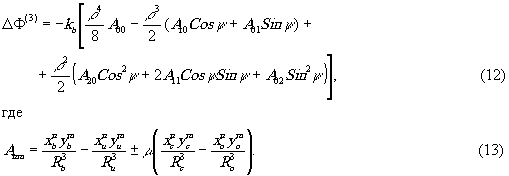
Здесь А 00 характеризует сферическую аберрацию, А01 и А10 -кому, а коэффициенты a20, a11 и А02 - астигматизм.
С помощью выражения (13) можно произвести анализ аберрационного состояния при разиичных условиях голографирования и восстановления изображений.
в) Оценка и экспериментальная проверка предельного разрешения голограммы как оптического элемента
Формулы (12) и (13) позволяют произвести оценку предельного разрешения в зависимости от условий голографирования и реконструкции изображения.
Для простоты рассмотрим случай голографирования и восстановления с помощью плоской опорной волны, т.е. ro= rb= 0 . Тогда, полагая допустимую сферическую волновую аберрацию на краю апертуры голограммы равной λb/4 , имеем:
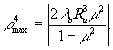 (14) (14)
Из (14) можно определить максимальный радиус голограммы ρ max. Зная ρmax можно найти и предельное разрешение nmax, ограничиваемое сферической аберрацией:
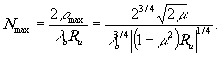 (15) (15)
Экспериментальная проверка производилась по максимальному разрешению голограммы, ограничиваемому сферической аберрацией при μ≠1. Для этого была снята на фотопластинке Кодак 649 f по одноосевой схеме голограмма точечного источника, получаемая в фокусе микрообъектива, способного давать вблизи оптической оси точку ~1 мкм. Опорная волна была плоской; расстояние от точечного источника до голограммы rc = 69 мм; λо= 632,8 нм. С помощью этой голограммы было получено изображение миры №2 с уменьшением в 3,75х при освещении с длиной волны λb= 546 нм. При этом максимальное разрешение оказалось равным 300 линий/мм. В то же время вычисленное по формуле (15) значение (μ=0,863, ru= 80 мм)
nm= 295 линий/мм.
г) Исследование аберраций косых пучков в голографии
Одним из возможных вариантов экспериментальной проверки вышеприведённых аберрационных расчётов голограмм является исследование аберраций косых пучков.
Уравнение (7), связывающее геометрические параметры опорного источника, объекта и его изображения было получено без учёта высших порядков разложения (5). Если же учесть и третий член разложения в (5), то вместо (7) получим выражения:
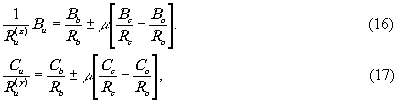
где bk = 1 - sin2θk cos 2φk
и ck = 1 - sin2θk sin 2φk.
Здесь 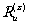 характеризуют расстояния от центра голограммы до изображения, образованного
лучами, лежащими в плоскости, параллельной оси x
и оси y, соответственно.
Таким образом,
характеризуют расстояния от центра голограммы до изображения, образованного
лучами, лежащими в плоскости, параллельной оси x
и оси y, соответственно.
Таким образом, 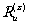 и и
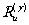 не одинаковы, подобно тому, как для косых пучков у линзы имеются два фокуса,
образуемые соответственно лучами, лежащими в сагиттальной и меридиальной плоскостях.
не одинаковы, подобно тому, как для косых пучков у линзы имеются два фокуса,
образуемые соответственно лучами, лежащими в сагиттальной и меридиальной плоскостях.
С целью проверки формул (16) и (17) были получены по двухосевой схеме голограммы резкой границы светлого поля при ориентировании последней параллельно и перпендикулярно полосам несущей решётки на голограмме.
Условия при съёмке голограмм: угол голографирования 10°; использовалась плоская опорная волна и объект также освещался плоской волной; расстояния от голограммы до объекта 310 мм, диаметр голограммы 20 мм; λо = 652,8 нм. Восстановление изображения производилось плоской волной.
Для наглядности рассуждений поместим голограмму в соответствии с рис.2 в плоскости (х, у) таким образом, чтобы полосы несущей решётки на голограмме были параллельны оси х. Очевидно, что в случае, когда резкая граница при голографировании была ориентирована параллельно несущей, при восстановлении изображение любой точки резкого края будет образовано лучами, лежащими в плоскости, параллельной оси x. Аналогично, при ориентации резкого края перпендикулярно несущей, изображение любой точки резкого края будет образовано лучами, лежащими в плоскости, параллельной оси х.
Было определено расстояние r u
от восстановленного изображения до голограммы при различных углах восстановления
для обеих голограмм, т.е. 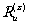 и и
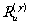 .
Результаты представлены в табл.1 (при изменении угла восстановления в плоскости
yz) и таблице 2 (угол восстановления
в этом случае изменяется таким образом,что при постоянном
θb .
Результаты представлены в табл.1 (при изменении угла восстановления в плоскости
yz) и таблице 2 (угол восстановления
в этом случае изменяется таким образом,что при постоянном
θb = 10°
φb
принимал значения от 0° до 360°). Там же приведены и результаты расчёта
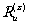 и и
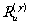 по формулам (16) и (17).
по формулам (16) и (17).
Таблица 1
|
θb˚
ru, мм |
φb = -90˚ φb = +90˚ |
|
25 |
20 |
15 |
10 |
5 |
0 |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
|
ru(y) расч.
ru(y) эксп.
ru(x) расч.
ru(x) эксп. |
200
203
310
310
|
230
228
310
310
|
254
252
310
310
|
276
273
310
310
|
292
290
310
310
|
302
301
310
310
|
308
308
310
310
|
310
310
310
310
|
308
308
310
310
|
301
301
310
310
|
291
291
310
310
|
275
276
310
310
|
260
260
310
310
|
Таблица 2
|
θb˚
ru, мм |
270 |
315 |
360 |
45 |
90 |
135 |
180 |
225 |
|
ru(x) расч.
ru(x) эксп.
ru(y) расч.
ru(y) эксп. |
309
310
312
310 |
303
305
312
309 |
298
301
304
301 |
301
305
284
283 |
309
310
276
272 |
303
305
282
283 |
297
301
302
301 |
302
305
312
309 |
Как видно из приведённых таблиц, совпадение экспериментальных и расчётных данных хорошее.
Таким образом, приведённые выше формулы аберраций голограмм могут быть использованы для инженерных расчётов.
Л и т е р а т у р а
1. l.mandel. josa, 56, 1636, 1966.
2. u.bertolotti. f.gori, s.guattfri. josa, 57, 1526, 1967.
3 . Г.Н.Буйков, А.В.Лунин, К.С.Мустафин. Оптика и спектроскопии,
28 , вып.5, 1018 (1970).
4. А.Марешаль, С.Франсон. Структура оптического изображения.
Изд. Мир, М., 1964.
5. Г.Н.Буйнов, А.В.Лукин, К.С.Мустафин. Оптика и спектроскопия,
28 , вып.4, 762 (1970).
6. f.w.meier. josa, 55, 987, 1965.
7. e.n.leith, j.upatnieks, k.a.haines. josa, 55, 981, 1965.
8. e.b.champagne. josa, 57, 51, 1967.
9. j.armstrong. ibm i.res.develop., 9,171, 1965.
10. e. В.champagne, n.g.massey. appl.opt., 8, 1879, 1969.
11. w.richter. qptica acta, 17, 285, 1970.
12. g.groh, c.h.f.velzel. qptik, 30, 257, 1969.
13. К.С.Мустафин, В.А.Селезнев. Оптика и спектроскопия, 29, 990 (1970).
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

