|
|
 |
 |

|
| |
О ВЛИЯНИИ НЕЛИНЕЙНОСТИ ФОТОМАТЕРИАЛА НА ДИФРАКЦИОННУЮ ЭФФЕКТИВНОСТЬ АМПЛИТУДНЫХ ГОЛОГРАММ
Г.Б.Семёнов, Ю.Н.Денисюк, Н.А.Савостьяненко
Показано, что влияние нелинейности фотоматериала на дифракционную эффективность амплитудных голограмм может быть учтено с помощью коэффициентов, которые зависят от контраста интерференционной картины, регистрируемой на голограмме, и от контрастности фотоматериала.
При регистрации голограмм на фотографических материалах в целом ряде случаев необходимо учитывать нелинейность регистрирующей среды.
В настоящее время достаточно подробно изучено влияние нелинейности на качество восстановленного изображения. В частности, показано, что при сравнимых величинах интенсивностей референтного и объектного пучков, используемых в процессе регистрации голограммы, помимо двух сопряжённых изображений в первом порядке дифракции, голограмма при её реконструкции образует также и дополнительные изображения в более высоких порядках дифракции: 2, 3 и выше. Причём все эти изображения, в том числе и изображения первого порядка, могут оказаться заметно искажёнными /1-3/. Известно также, что вследствие нелинейности регистрирующего материала может нарушиться относительное распределение освещённости в изображении сложного объекта, особенно в тех случаях, когда объект состоит из нескольких точек, сильно отличающихся по яркости /4/.
В значительно меньшей степени исследовано влияние нелинейности регистрирующей среды на так называемую дифракционную эффек-
тивность голограммы - отношение величины потока излучения, образующего реконструированное голограммой изображение, к величине потока, падающего на голограмму при реконструкции. Пожалуй, единственной работой по этому вопросу является работа Вьянта и Гивенса /5/, в которой было исследовано влияние коэффициента контрастности фотоматериала на соотношение освещённостей в изображении многих точек, записанных на одной голограмме по методу последовательной регистрации. Полученные авторами выражения позволяют определить дифракционную эффективность голограмм с учётом нелинейности фотоматериала, однако требуют громоздких расчётов.
В настоящей работе был проведён аналяв дифракционной эффективности голограаи, зарегистрированных на нелинейном фотоматериале, в результате которого получены графические зависимости, позволяющие в значительной степени сократить объём вычислений. Особенность этого анализа состоит в том, что дифракционная эффективность представлена в виде произведения двух сомножителей. Один из сомножителей представлявляет собой линейную составлявшую дифракционной эффективности, которая может быть вычислена о помощью простого выражения по известным значениям средней амплитудной прозрачности голограммы τ 0, коэффициенту контраста интерференционной картины, регистрируемой на голограмме р и коэффициенту контрастности фотоматериала γ, а другой сомножитель, названный нами коэффициентом нелинейности, учитывает влияние нелинейности фотоматериала на дифракционную эффективность голограммы. Значения этого коэффициента представлены в виде графиков зависимости от р для нескольких значений γ. В работе приведены также выражения и графики для расчёта величины светового потока, который дифрагирует во второй порядок спектра, образованного голограммой.
Рассмотрим дифракционную эффективность амплитудных двумерных голограмм для случая произвольных величин р и γ. Пусть волновые функции объектного и референтного излучения определяются в плоскости регистрации голограмм хоу, следующими выражениями:
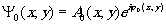 , (1) , (1)
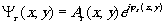 , (2) , (2)
где a(x,у) и φ(х,у) - значения амплитуды и фазы излучения в некоторой точке с координатами х и у.
Распределение интенсивности в плоскости голограммы можно записать тогда следующим образом:
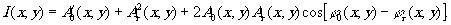 (2) (2)
Глубина модуляции интерференционной картины распределения интенсивности характеризуется коэффициентом контраста
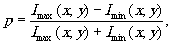 (4) (4)
где imax и imin - максимальное и минимальное значения интенсивности интерференционной картины. Подставляя в (4) значения imax и imin , полученные с помощью (5) найдём
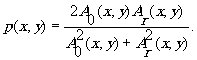 (5) (5)
Используя (5), выразим распределение интенсивности в плоскости голограммы через коэффициент контраста
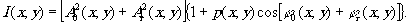 (6) (6)
Параметр р, входящий в формулу (6), зависит в общем случае от координат, т.е. контраст интерференционной картины различен для различных областей голограммы. Ограничим дальнейшее рассмотрение случаем, когда объект и референтный источник удалены от голограммы на расстояние, много большее её размеров. Тогда можно считать, что А 0 и Аr, а следовательно, и р не зависят от координат.
Предположим, что распределение интенсивности (6) зарегистрировано на фотоматериале. В общем случае амплитудная прозрачность полученной голограммы является комплексной функцией координат х и у.
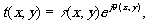 (7) (7)
где τ(х,у) характеризует изменение амплитуды волны, a θ(x,σ)-изменение её фазы при прохождении через голограмму. В дальнейшем мы будем считать, что голограмма имеет одинаковую толщину, т.е. θ не зависит от координат х и у. Практически это имеет место, если поместить голограмму в иммерсионную среду. При этом предположении амплитудная прозрачность обработанной голограммы связана с прозрачностью по интенсивности Т(х,у) следующим простым соотношением:
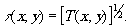 (8) (8)
Для линейного участка характеристической кривой фотоматериала прозрачность по интенсивности Т и экспозиция Н связаны, как известно, следующим образом:
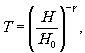 (9) (9)
где γ - коэффициент контрастности фотоматериала, численно равный тангенсу угла наклона кривой, а Н0- точка инерции фотоматериала. Экспозиция Н пропорциональна интенсивности излучения i.
h=ci. (10)
Используя формулы (6), (8) - (10), можно записать следующее выражение для амплитудной прозрачности голограммы:
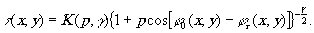 (11) (11)
Здесь
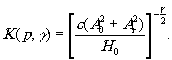 (12) (12)
Значение волновой функции Ψ (x,y) излучения, восстановленного голограммой в плоскости самой голограммы, найдём, умножая волновую функции восстанавливающего источника (2) на амплитудную прозрачность голограммы (11)
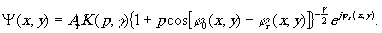 (13) (13)
Функция Ψ(х,у) представляет собой граничное условие, из которого можно найти распределение поля во всём пространстве за голограммой. Это поле особенно легко найти в так называемом случае линейной записи, когда каждой пространственной гармонике распределения интенсивности при записи соответствует при реконструкции единственная гармоника того же периода. Как известно, этот случай может быть реализован для любого значения γ фотоматериала, если голограмму записать с очень малым контрастом. В частном случае, когда γ = -2, линейность записи сохраняется пря любом значении р.
Запишем выражение для волновой функции восстановленного голограммой излучения в случае линейной записи, когда величина параметра р значительно меньше i. Раскладывая выражение в фигурных скобках в формуле (15) в биномиальный ряд и пренебрегая членами этого ряда, содержащими параметр р в степенях выше первой, получим
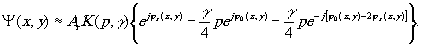 (14) (14)
Нетрудно заметить, что первый и второй члены этого выражения с точностью до постоянных множителей совпадают с волновыми функциями объектного и референтного пучков (1,2). В силу однозначности связи граничных условий с волновой функцией именно эти волновые поля и будут восстановлены в пространстве, расположенном
за голограммой. Можно показать, что третий член выражения (14) также удовлетворяет волновому уравнению, и соответствующее ему излучение образует так называемое ложное изображение.
При нелинейной записи задача наховдения волновой функции, которая, подчиняясь волновому уравнению, удовлетворяет на поверхности голограммы граничному условию (13), существенно усложняется. Для нахождения такой функции воспользуемся тем обстоятельством, что в рассматриваемом случае, когда р не зависит от координат, член в квадратных скобках выражения (13) остаётся чётной периодической функцией разности фаз [φ 0(x,y)- φr(x,y) ] при любом значении γ. Очевидно, что в этом случае функция Ψ(х,y) может быть представлена в виде ряда Фурье по косинусам [φ0(x,y)- φr(x,y)]:
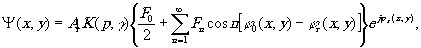 (15) (15)
где
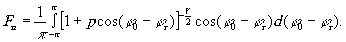 (16) (16)
Можно показать, что при достаточно малых углах между объектным и референтным лучами по крайней мере несколько первых членов (15) соответствуют обычным бегущим волнам, распространяющимся в пространстве за голограммой. При этом, как видно из (15) и (16), первым двум членам ряда соответствуют недифрагированное излучение, а также истинное и ложное изображения, аналогичные случаю линейной записи. Члены более высокого порядка описывают пространственно разделенные пучки, которые, однако, не образуют какого-либо изображения. И, наконец, начиная с некоторого значения n, членам ряда (15) соответствуют волны, затухающие в непосредственной близости от голограммы.
Для определения дифракционной эффективности голограмм необходимо знать поток Ф n излучения, дифрагированного в искомое изображение. Амплитуда излучения, образующего этот поток,определяется коэффициентом при втором члене разложения (15). В соответст-
вии с этим выражение для потока Ф n можно записать в следующем виде:
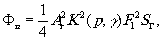 (17) (17)
где sг- площадь голограммы.
Дифракционную эффективность голограммы d найдём, отнеся (17) к величине потока, падающего на неё при реконструкции
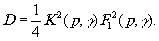 (18) (18)
Коэффициент К(р,γ) удобнее выразить через постоянную составляющую амплитудной прозрачности экспонированной голограммы τ 0, которую легко измерить экспериментально. Учитывая, что τ0 соответствует первый член разложения (15), получим
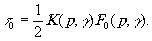 (19) (19)
Подставляя (19) в (18) и проведя некоторые преобразования, найдём
d=d Λkh (20)
где
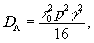 (21) (21)
а
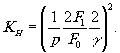 (22) (22)
Таким образом, выраяение для дифракционной эффективности может быть представлено в виде двух сомножителей dΛ и kh. Можно показать, что из этих сомножителей - dΛ в точности соответствует дифракционной эффективности голограммы для случая линейной записи. Действительно, в соответствии с (14) амплитуда волны, дифрагированной в один из первых порядков, определяется сяедувдим образом :
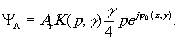 (23) (23)
Величина потока, образующего одно из изображений, определяется при этом как
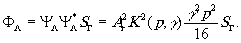 (24) (24)
Учитывая, что падающий на голограмму поток равен 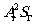 и что для случая линейной записи
и что для случая линейной записи
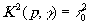 ,
получим следующее выражение для dΛ: ,
получим следующее выражение для dΛ:

Из сказанного следует, что влияние нелинейности фотоматериала на дифракционную эффективность в рассматриваемом случае полностью учитывается коэффициентом КН (22). Зависимость этого коэффициента от параметров р и γ можно найти следующим образом. Разложим выражение в квадратных скобках (16) в биномиальный ряд и выполнив интегрирование, получим выражение для коэффициентов f0 и f1. Подставляя полученные выражения в (22), найдём
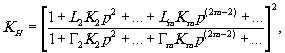 (25) (25)
где
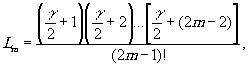 (26) (26)
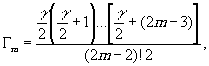 (27) (27)
Входящие в (25) значения km для первых 16 членов рядов приведены в таблице 1. Используя формулы (25)÷(27) и значения km из таблицы 1, можно подсчитать коэффициенты нелинейности,а следовательно, и дифракционную эффективность голограмм для широкого диапазона значений р и γ.
Таблица 1
Значения коэффициентов km выражении (25)
|
к 1 |
к 2 |
к 3 |
к 4 |
к 5 |
к 6 |
к 7 |
к 8 |
|
1 |
0,75 |
0,63 |
0,55 |
0,49 |
0,45 |
0,42 |
0,39 |
|
к 9 |
к 10 |
к 11 |
к 12 |
к 13 |
к 14 |
к 15 |
к 16 |
|
0,37 |
0,35 |
0,33 |
0,32 |
0,30 |
0,28 |
0,26 |
0,25 |
На рис.1 приведены вычисленные таким образом зависимости коэффициента КН от р для нескольких значений γ. Как видно из
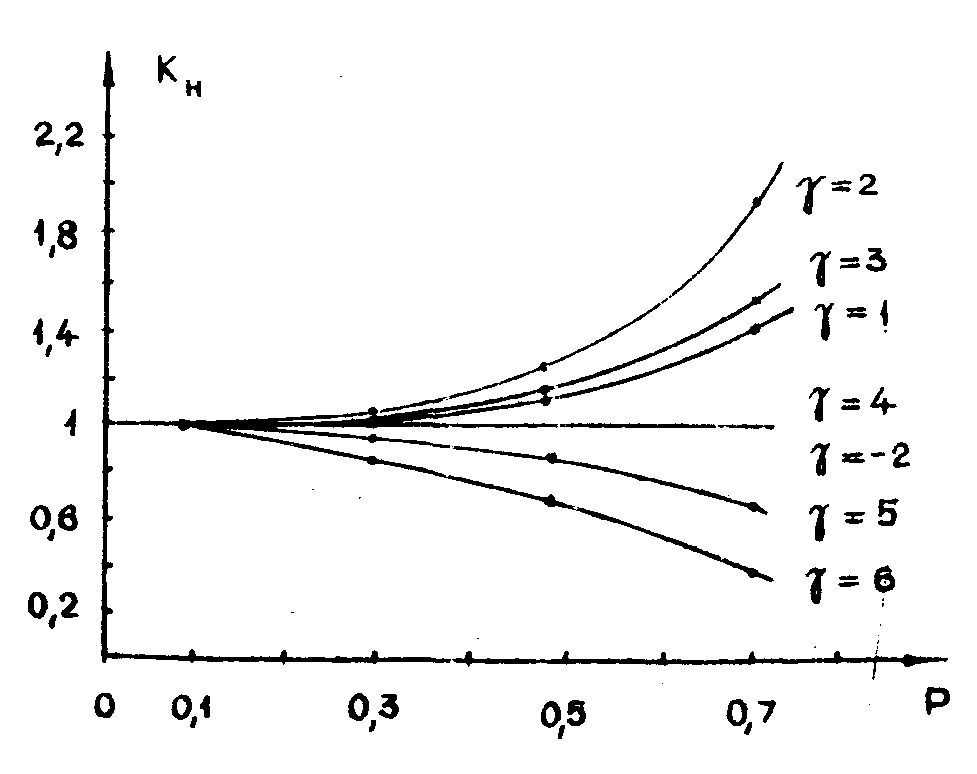
Рис.1. Зависимость коэффициента нелинейности kН от глубины модуляции интерференционной картины р для нескольких значения коэффициента контрастности фотоматериала γ .
На рис.1 приведены вычисленные таким образом зависимости коэффициента КН от р для нескольких значений γ. Как видно из рисунка 1, эффекты нелинейности начинают заметно влиять на дифракционную эффективность, начиная со значений р≈0,3. Как и следовало ожидать, при γ = -2 эффекты нелинейности отсутствуют при любых значениях р. Несколько неожиданным оказалось то, что эффекты нелинейности не влияют на дифракционную эффективность голограммы и при γ=4. Однако этот случай всё же не эквивалентен линейной записи, поскольку изображения высших порядков при этом не исчезают.
Использованный нами метод рассмотрения влияния нелинейности фотоматериала на дифракционную эффективность голограмм позволяет также определить количество света, дифрагированного в любой из высших порядков. Так, например, отношение потока излучения, дифрагированного в один из вторых порядков, к потоку излучения, падающему на голограмму при реконструкции, можно вычислить с помощью формулы, аналогичной формуле (20):
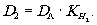 (28) (28)
При этом d определяется
с помощью выражения (21), а 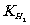 можно выразить через названные выше параметры р и γ следующим образом:
можно выразить через названные выше параметры р и γ следующим образом:
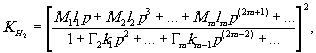 (29) (29)
где
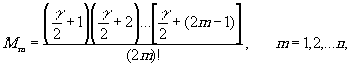
а Г m,
определяется с помощью выравения (27). Входящие в (29) значения lm
для первых 16 членов ряда приведены в таблице 2. На рисунке 2 изображены вычисленные
с помощью формул (27), (29) и (30) графики зависимости коэффициента 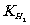 от р дяя нескольких значений γ.
Κак видно из этого рисунка,
величина
от р дяя нескольких значений γ.
Κак видно из этого рисунка,
величина 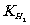 обращается в нуль при γ = -2 для любой величины контраста р, а также стремится
к нуле для любого γ при уменьшении р. Оба эти случая соответствуют линейной
записи и характеризуются отсутствием дифрагиро-
обращается в нуль при γ = -2 для любой величины контраста р, а также стремится
к нуле для любого γ при уменьшении р. Оба эти случая соответствуют линейной
записи и характеризуются отсутствием дифрагиро-
Таблица 2
Значения коэффициентов lm выражения (29)
|
l1 |
l2 |
l3 |
l4 |
l5 |
l6 |
l7 |
l8 |
|
0,5 |
0,5 |
0,47 |
0,44 |
0,41 |
0,39 |
0,37 |
0,35 |
|
l9 |
l10 |
l11 |
l12 |
l13 |
l14 |
l15 |
l16 |
|
0,33 |
0,32 |
0,3 |
0,27 |
0,26 |
0,24 |
0,23 |
0,22 |
ванного света в высших порядках дифракции (выше первого). Однако по мере увеличения
контраста величина 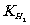 начинает заметно расти, что соответствует увеличению интенсивности света во
втором порядке дифракции. Из рис.2 также следует, что увеличение коэффициента
контрастности фотоматериала γ при одном и том же значении р приводит к
увеличению
начинает заметно расти, что соответствует увеличению интенсивности света во
втором порядке дифракции. Из рис.2 также следует, что увеличение коэффициента
контрастности фотоматериала γ при одном и том же значении р приводит к
увеличению 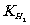 . .
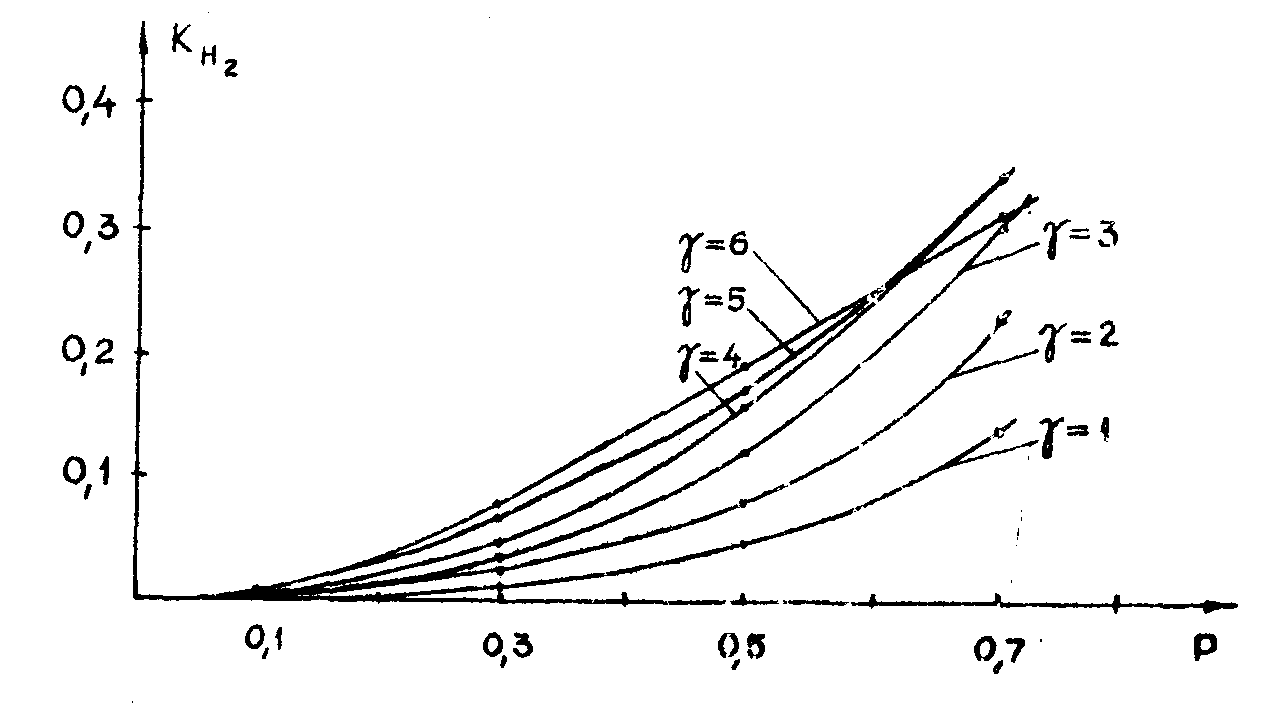
Рис.2. Зависимость коэффициент нединейностм 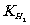 от глубины модуляции интерференционной картины р для несколькм значений
коэффициента контрастности фотоматериала γ.
от глубины модуляции интерференционной картины р для несколькм значений
коэффициента контрастности фотоматериала γ.
Для проверки основных положений теории были измерены дифракционные эффективности
d и d2
нескольких голограмм с различными р, γ и 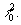
На голограммах записывалась картина интерференции двух плоских волн, распространяющихся под углом 30 мин. друг к другу. При этом регистрация осуществлялась на фотоматериале с разрешающей способностью порядка 100 лин./мм (фотоплёнка изопанхром, тип 17). Коэффициент контраста этой картины р рассчитывался, исходя из соотношения интенсивностей интерферирующих волн, которое измерялось с помощью ФЭУ. Для измерения γ рядом с голограммой на фотоплёнке регистрировалась сенситограмма, с помощью которой строилась соответствующая характеристическая кривая фотослоя. С помощью такой характеристической кривой можно было судить также о том, находятся ли изменения оптической плотности голограммы в пределах линейного участка характеристической кривой.
Для устранения фазовой модуляции голограммы помещались при измерениях в иммерсионную среду. В качестве иммерсии нами были использованы бензин и дистиллированная вода. Показатель преломления бензина nδ= 1,5 был близок к показателю преломления сухого эмульсионного слоя (nc=1,52). Показатель преломления дистиллированной воды (nb= 1,33) был близок к показателю преломления размоченного слоя.
В процессе реконструкции голограмм с помощью ФЭУ были измерены величины потоков,
дифрагированных в первый и второй порядки, а такие потока излучения, прошедшего
через неэкспонированную проявленную и отфиксированную часть фотоплёнки той же
площади, что и голограмма. Дифракционные эффективности голограмм d и
d2 вычислялись как отношение
первой или второй из этих величин к третьей. Величина 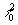 измерялась аналогичным образом через отношение недифрагированной части излучение
к излучению, прошедшему через неэкспонированный проявленный и отфиксированный
фотослой.
измерялась аналогичным образом через отношение недифрагированной части излучение
к излучению, прошедшему через неэкспонированный проявленный и отфиксированный
фотослой.
Полученные таким образом значения d и d2 приведены в таблице 3. В этой же таблице представлены теоретические значения
Таблица 3
Экспериментальные и теоретические значения дифракционной эффективности амплитудных голограмм
|
Иммерсия - дистиллированная вода |
|
p |
γ |
|
d |
dt |
d2 |
dt2 |
|
0,71
0,45
0,68
0,55
|
1,5
1,7
1
1 |
0,037
0,085
0,205
0,215 |
3,8·10-3
3,6·10-3
8,9·10-3
5·10-3 |
4,1·10-3
3,7·10-3
8,3·10-3
5·10-3 |
3,16·10-4
8,5·10-5
2,29·10-4
8,8·10-5 |
4,8·10-4
15·10-5
7,25·10-4
25·10-5 |
|
|
Иммерсия - бензин |
|
|
|
0,71
0,45
0,68
0,55 |
1,5
1,7
1
1 |
0,026
0,063
0,19
0,185 |
4·10-3
3,7·10-3
1,3·10-3
7,7·10-3 |
3,1·10-3
2,6·10-3
7,7·10-3
4,3·10-3 |
3,7·10-4
1,1·10-4
3,3·10-4
1,3·10-4 |
3,3·10-4
1,4·10-4
6,7·10-4
2,2·10-4 |
эффективностей dТ и dТ2, вычисленные с помощью формул (20),(21), (28) и графиков, изображенных на рис.1 и 2.
Из таблицы 3 видно, что в первом порядке дифракции при использовании в качестве иммерсии воды отличие экспериментальных значений d от теоретических не превышает 10%, что является достаточно хорошим совпадением. Однако при использовании в качестве иммерсии бензина в тех же порядках дифракции наблюдается заметное превышение измеренных значений d над теоретическими. Это можно объяснить тем, что бензин устраняет только ту часть фазовой модуляции, которая обусловлена наличием регулярного рельефа на поверхности голограммы. По-видимому, существует ещё заметная модуляция показателя преломления в обработанном фотослое. В разбухшем в воде слое эта часть модуляции исчезает и голограмма становится чисто амплитудной.
Во вторых порядках дифракции наблюдается заметное расхождение экспериментальных и теоретических значений эффективности. Причём во всех случаях, когда в качестве иммерсии использован бензин, эти расхождения заметно меньше, чем при использовании воды. Можно предположить, что при разбухании эмульсии в воде происходят небольшие искажения рисунка голограммы, к которым вторые порядки дифракции обладают значительно более высокой чувствительностью, чем первые.
Л и т е р а т у р а
1. a.kozma. josa, 56, 428, 1966.
2. j.w.goodman, g.r.knight. josa, 58, 1276, 1968.
3. o.bryngdahl, А.lohmann. josa, 58, 1325, 1968.
4. a.a.friesem, j.s.zelenka. appl.opt., 6, 1755, 1967.
5. j.q.wyant, m.p.givens. josa, 58, 357,1968.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

