Media-security

ДИФРАКЦИИ КОГЕРЕНТНОГО СВЕТА И ЕЁ ИСПОЛЬЗОВАНИЕ В ГОЛОГРАФИИ

Н.М.Померанцев

Изложены основы дифракции когерентного света. Дана классификация голограим по виду дифракции. Кратко рассмотрен вопрос о записи полной информации на голограммах.

В в е д е н и е

Явление дифракции используется в голографии при восстановлении голограмм и в некоторых системах обработки информации. Чтобы ясно представить себе всю картину этого явления, необходимо рассмотреть законы распространения когерентного света, из которых следует явление дифракции.

Описание распространения света (в отличие от процессов испускания и поглощения) возможно в рамках электромагнитной теории, т.е. в предположении, что распространение света происходит по тем же законам, что и распространение электромагнитных воян в обычной классической теории.

Рассмотрим возникновение и совершенствование представлений о законах распространения света.

1. Распространение световых волн при передаче информации

а) История вопроса

Законы распространения световых волн начали изучаться задолго до появления электромагнитной теории света. Полезно кратко рассмотреть эволюцию формулировок этих законов. Ещё в конце 17 века, в период господства механических представлений о природе световых явлений Гюйгенс сформулирован принцип, носящий его имя и определяющий закон распространения единичного возмущения в упругой среде.

Согласно этому принципу каждая возмущённая точка упругой среды (т.е. сдвинутая в пространстве точка) может рассматриваться как центр нового (вторичного) возмущения. Вторичные возмущения, складываясь, порождают фронт распространения возмущения.

Основным достоинством принципа Гюйгенса, особенно важным для голографии, является то его положение, что можно забыть об источнике света, породившего фронт волны,и рассматривать только этот фронт в любой момент времени и в любой области пространства. Перефразируя это положение принципа Гюйгенса на современный лад, можно его выразить так: фронт волны, испущенной источником света, несёт информацию об этом источнике. Учитывая всё сказанное, можно считать, что Гюйгенс был тем исследователем, который заложил первый камень в фундамент здания голографии. Итак, история развития голографии насчитывает почти 500 лет.

Немногим более чем через 100 лет после Гюйгенса Френель сделал попытку распространить его принцип на периодические процессы, происходящие, однако, также в упругой среде, так называемом "эфире", которого, как кы сейчас знаем, представить себе невозможно. Строгого обоснования у Френеля этот принцип, однако, не получил.

Особенностями принципа Гюйгенса-Френеля является необходимость принятия дополнительных предположений, не вытекающих из самого принципа. Одним из дополнительных предположений является необходимость принять, что вторичные возмущения,рассматриваемые как центры новых возмущений, исходящих из вторично возмущённых точек

среды, распространяются только в одним направления.

Другим дополнительным предположением является необходимость вводить в формулы сдвиг фазы на π/2 , νе следующий из формулировки принципа.

Обратим внимание на то, что если задаётся только одна скалярная волновая функция, одному и тому же распределению амплитуд и фаз единичных волн будут соответствовать два волновых фронта (рассматриваемые как огибающие единичных сферических волн). Один из этих фронтов распространяется в одну сторону от поверхности, а другой - в противоположную. Неудивительно, что для однозначности решения приходится принимать дополнительные, не включённые в формулировку задачи предположения о направлении распространения воля и сдвиге их фаз. Другими словами, при такой постановке задачи не задана необходимая информация о том, в какую сторону должны распространяться волны. Ниже мы увидим, что подобная же ситуация существует в случае тонкослойных голограмм.

Позднее Кирхгоф пытался преодолеть эти недостатки принципа Гюйгенса-Френеля, использовав стационарное уравнение для волн, описываемых скалярной функцией, и теорему Грина.

При решении такой задачи он предположил, что скалярная волновая функция и её производная по нормали в отверстии задаются волной, падающей на эти отверстия извне, а на остальной части экрана как функция, так и её производная, равны нулю.

Такое предположение противоречит теореме Грина, из которой следует, что волновая функция вместе со своей производной не может обращаться в нуль ни в одной точке пространства, так как иначе она будет тождественно равна нулю во всей пространстве. Поэтому решение Кирхгофа нельзя назвать математически строгим.

Несмотря на это, решение Кирхгофа успешно применялось при решении рада задач о дифракиии и давало результаты, хороио совпадающие с эксперинентальяши данными. Это можно объяснить тем, что влияние экрана сказывается ляшь непосредственно у самого края отверстия, т.е. в зоне, включавшей всего несколько длин волн.

Существенного несогласия решения Кирхгофа с практически наблюдаемым распределением поля можно ожидать лишь в случаях, когда размеры отверстия сравнимы с длиной волны. Это имеет место, например, в радиодиапазоне. В оптике подобных случаев практически не встречается.

Однако формула Кирхгофа имеет и другой недостаток. Она основывается на решении скалярного волнового уравнения, а не на решении уравнений Максвелла для векторов электрического и магнитного поля, как этого требует электромагнитная теория света.

После работ Кирхгофа проблемой распространения света занималось значительное число исследователей. Останавливаться на их работах нет возможности. Рассмотрим лишь одно из решений, имеющее ясный физический смысл и позволяющее после ряда упрощений (на которых мы акцентируем в дальнейшем внимание) получить формулы, удобные для расчётов. Как оказалось, идея этого решения была вы сказана ещё в 1914 году Л.И.Мандельштамом.

б) Векторный аналог формулировки принципа Гюйгенса-Френеля

Для нахождения напряжённости электромагнитного поля внутри некоторого замкнутого объема v, ограниченного поверхностью s, в котором нет источников поля (рис.1), поместим в исследуемую точку вспомогательный электрический диполь, колеблющийся с частотой ω, излучающий электромагнитные волны и создающий внутри исследуемой области электрические и магнитные поля 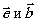. В общем случае поля диполей могут быть определены только после задания граничных условий на поверхности s или структуры внешнего относительно области v пространства. Однако, как это следует из теории, для вспомогательного диполя, введённого выше, можно выбрать структуру пространства однородной, а поля 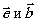удовлетворяющими уравнениям Максвелла в форме, приводимой ниже.

Мы будем рассматривать однородное (как внутри, так и вне v ) пространство и описывать поля 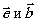с помощью хорошо известного вектора Герца электрического типа , который имеет ясный физический смысл и описывает электрический диполь. Для целей голографии достаточно рассматривать только стационарные поля, когда

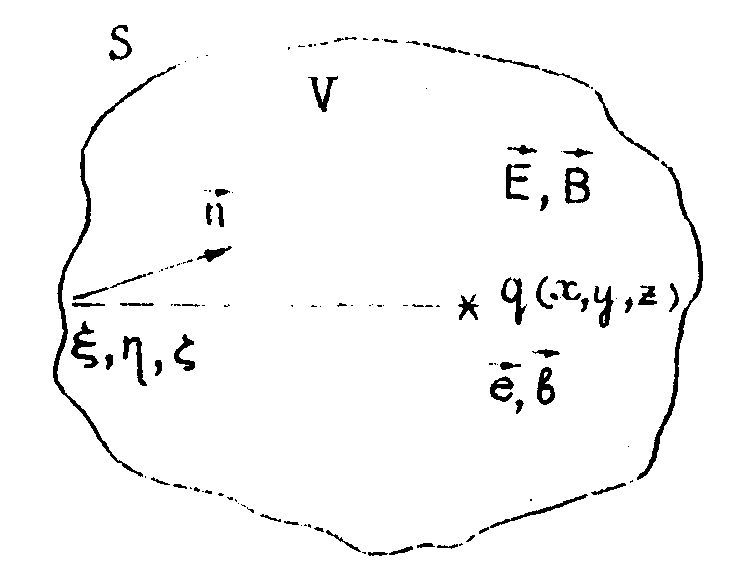
Рис.1. Поверхность (s), окружающая объём (v), внутри котирого, в точке q, определяется напряжённость метрического (Е) и магнитного (В) полей. Векторы 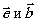определяют электромагнитное поле, создаваемое точечным электрическим диполем, помещённым в точку q.

зависимость от времени имеет вид .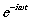

Поле, обусловленное вектором Герца электрического гипа:

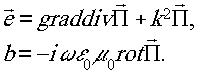
Вектор Герца подчиняется однородному векторному волновому уравнению

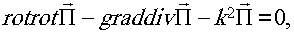
решение которого мы принимаем в виде

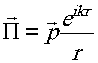
В атом выражении 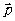- вектор силы диполя, который может быть взят произвольным

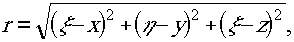
где ξ, η, ξ - κоординаты системы координат, связанной с поверхностью; х, y, z - координаты точки q.

Искомые электрическое и магнитное поля обозначим символами 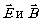. Предполагаем, что они так же, как и векторы 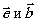удовлетворяют уравнениям Максвелла:

Умножая эти уравнения скалярно на 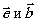, а также уравнения Максвелла для 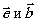на Е и В , складывая и применяя известные формулы векторного анализа, получим лемму Лоренца:

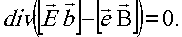
Интегрируя выражения для леммы Лоренца по объёму v и применяя к полученному результату формулу Гаусса, позволяющую переходить от интегралов по объёму к интегралам но поверхности, получим

где 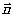- вектор нормали, направленный внутрь поверхности; s₀ -сфера малого радиуса, которой необходимо окружить точку q нахождения диполя, так как эта точка является особой точкой поля.

Уменьшая сферу s₀ до бесконечно малой при переходе к пределу s₀→0, получим

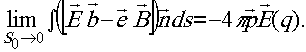
Проделав те же выкладки для области пространства внешней по отношению к v и сравнивая результаты вычислений, получим ряд теорем взаимности, суть которых применительно к теореме для электрического поля можно изложить следующим образом.

Если имеются два электрических диполя с силами , колеблющихся с одинаковой частотой и излучающих поля 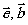и Е, В, соответственно, то имеет место следующее соотношение:

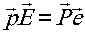Аналогичные соотношения можно получить также для магнитных диполей и магнитного поля (кроме того, можно получить аналогичные соотношения для магнитного вектора Герца , удовлетворяющего тому же волновому уравнению, что и вектор ).

Применяя теоремы взаимности и перестановочные соотношения векторного анализа к приведённым выше интегралам, нетрудно получить выражение, в котором вектор может быть вынесен за знак интеграла (так как он не зависит от координат, по которым ведётся интегрирование) и появляется в виде векторного коэффициента при каждом члене уравнения.

Таким образом, вектор (вектор силы диполя) становится лишь произвольным вспомогательным вектором, который помогает получить решение, но не оказывает влияния на величину напряжённости искомого электрического и магнитного поля. Мы как бы сначала помещаем в точку наблюдения электрический диполь, выражаем поле в точке q через поле, создаваемое диполем на границе области, а затем диполь удаляем.

Окончательное выражение для вектора напряжённости электрического поля будет следующим:

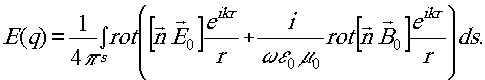
Эта формула является векторным аналогом формулы принципа Гюйгенса-Френеля и определяет ноле в заданной точке q внутри области пространства, лишенной источников, через поверхностную плотность электрических и магнитных диполей, распределённых на заданной поверхности, окружающей точку q. В некоторых частных случаях поверхность s может быть увеличена и превращена в бесконечную плоскость.

Таким образом, векторный аналог принципа Гюйгенса-Френеля может быть представлен в следующей формулировке: элeктpoмaгнитнoe поле внутри заданной области v, ограниченной поверхностью, тождественно полю электрических и магнитных диполей, распределённых на геометрической поверхности s с поверхностной плотностью электрических и магнитных сил диполей, составляющей, соответственно,

где 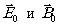- поля на поверхности s.

Из этой формулировки принципа Гюйгенса-Френеля непосредственно следует, что излучение источника света (или предмета, отражающего свет), расположенного внутри некоторой области, может быть заменено распределением на поверхности этой области электрических и магнитных диполей, т.е. другими словами - голограммой.

Приведённое выше выражение для вектора электрического поля в точке q показывает, что когерентный свет распространяется в однородном пространстве по сложному закону и контуры предмета, испускающего (или отражающего) свет, преобразуются при распространении света в произвольном направлении довольно сложным образом.

Необходимо всё же отметить, что благодаря линейности уравнений Максвелла преобразование, которое выражает формула векторного аналога принципа Гюйсгенса-Френеля, оказывается также линейным и преобразование информации при распространении света в свободной пространстве можно рассматривать как преобразование, произведённое линейным фильтром, общая теория временных линейных фильтров и линейных преобразований довольно подробно описана у литературе и нет необходимости на ней останавливаться. Отметим лишь два отличия фильтров пространственных сигналов (т.е. фильтров, преобразующих пространственную информацию - информации о контурах и других особенностях предметов) от фильтров врученных сигналов. Первой особенностью является возможность изменения при странственных координат как в положительном, так и в отрицательном направлении (время, как мы знаем, может изменяться только в положительном направлении). Второй особенностью является то, что в общем случае преобразование пространственной информации не инвариантно к изменению начала отсчёта пространственных координат (из-за множителя e^ikr/r) и только в частном счучае такая инвариантность имеется. Временные линейные фильтры всегда инвариантны к изменению начала отсчёта времени.

Как уже было сказано, приведённое выше преобразование довольно сложно и неудобно для практических расчётов. Однако, если изложить определённые ограничения на положение точки q в пространстве и на размеры поверхности, на которой распределены электрические и магнитные диполи, то выражения для вектора полн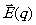

упрощается и формула, выражающая принцип Гюйгенса-Френеля, становится близкой к той, которую ей придал в свое время Френель.

в) Приближения, необходимые для получения

практически используемых формул

Рассмотрим те ограничения, при которых из приведённой выше формулы векторного аналога принципа Гюйгенса-Френеля, выведенной из законов электродинамики, получатся формулы преобразований, обычно применяемых при теоретических расчётах в голографии.

Введём следующие ограничения.

1. Поверхность, по которой распределены электрические и магнитные диполи, является волновой поверхностью, т.е. представляет собой фронт волны, испущенной каким-либо источником света.

Тогда векторы 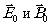будут перпендикулярны вектору нормали 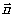(рис.2) и можно положить

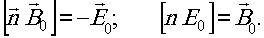
Для удобства введем обозначение e^ikr/r = φ.

После введения первого ограничения выражение для электрического поля примет вид

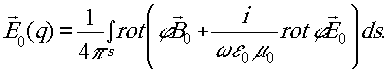
2. Расстояние r велико по сравнению с максикальным размером поверхности, на которой распределены электрические и магнитные диполи.

На основании этого ограничения при дифференцировании функции φ величину r в знаменателе можно считать постоянной.

3. Точка q, в которой определяется поле, лежит на восстановленной из начала координат нормали к поверхности s (или близка к этой нормали).

Из этого ограничения следует, что для grad φ можно принять выражение .

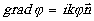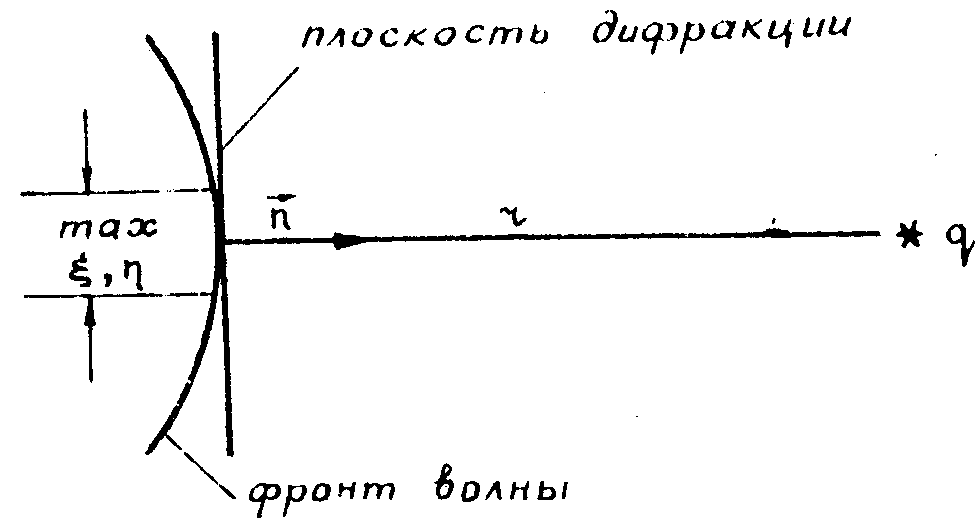
Рис.2. Плоскость дифракции, фронт падающей на неё волны, размеры области дифракции и положение точки q, в которой необходимо определить электромагнитное поле при приближенном методе расчёта. Вектор 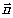является вектором нормали к поверхности волнового фронта.

Последнего ограничения, правда, нетрудно избежать, но в голографии употребляются формулы, полученные с учётом всех трёх ограничений.

Для пояснения всех введённых ограничений приводим рис.2. Ограничения позволяют упростить подынтегральное выражение и получить

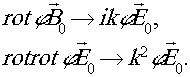
После введения всех трёх ограничений из сложного выражения векторного аналога принципа Гюйгенса-Френеля получается более

простое

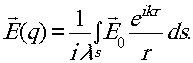
Это выражение несущественно отличается от выражения, полученного Френелем, но именно из него получаются формулы преобразований, применяемых при практических расчетах в голографии.

Можно ещё упросить эту формулу. Разложим величину

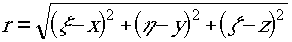
в ряд по малому параметру 1/r , где r = ζ - z - расстояние между системой электрических и магнитных диполей, распределённых по поверхности s, и точкой q, в которой определяется поле. Величину и благодаря ограничению п.2 можно считать не зависящей от координат, так как максимальные величины координат ξ, η, ζ θ х, y, z оказываются малыми по сравнению с r. В результате почучим

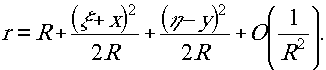
Формула, выражающая принцип Гюйгенса-Френеля, принимает теперь вид

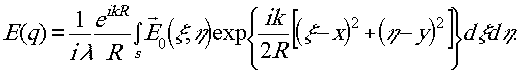
Итак, в результате трёх, наложенных на положение точки q, ограничений мы получили выражение, носящее название преобразования Френеля. Это преобразование определяет закон, по которому при распространении света в однородной пространстве преобразуются контуры предметов, испускающих или отражающих когерентный свет. Другими словами, информация о предмете передаётся в рассмотренном приближении посредством преобразования Френеля.

г) Прохождение световых волн через модулирующие среды

Остановимся немного на модулирующих средах.

В голографии и при обработке информации с помощью когерентного света применяются различные модулирующие, т.е. преобразующие информацию среды (название "модулирующие" заимствовано из теории передачи временных сигналов и может быть заменено общим названием "преобразующие"). Необходимо помнить, что сам характер принципа Гюйгенса-Френеля не позволяет применять его для любого случая распространения света в произвольной среде. Поэтому необходимо выделить те случаи, к которым он применим. Поскольку согласно принципа Гюйгенса-Френеля источником поля является поверхностная плотность электрических и магнитных диполей, то очевидно, что этот принцип применим только в случае тонких модулирующих сред,

разнесённых на значительные расстояния в однородном пространстве. Понятие "тонкий", конечно, относительно и требует уточнения, но в данном случае следует рассматривать идеально тонкие среды, т.е. такие, которые в направлении одний координаты изменяют свои свойства на протяжении менее чем одной длины волны, а на всём остальном направлении однородны.

Здесь нет возможности, а также и необходимости описывать все модулирующие среды, применяемые в голографии. Ограничимся одним примером, который будет необходим в дальнейшем. Рассмотрим систему (рис.3), состоящую из транспаранта (на которой нанесено какое-нибудь изображение), освещённого параллельным пучком лучей света, сферической линзы, помещённой на расстоянии d от транспаранта, и экрана, расположенного на расстоянии d, от линзы. Рассмотрим преобразование информации при прохождении света от транспаранта до экрана. Распространение света в свободной пространстве между транспарантом и линзой, а также между линзой и экраном определяется преобразованием Френеля.

Сферическая линза изменяет только фазу прошедшего через нее света, что описывается в первом приближении функцией

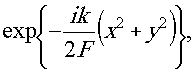
где f- фокусное расстояние линзы. Преобразование фазы, описываемое такой функцией, может быть осуществлено только с помощью линзы, которую можно назвать идеальной. На практике применяют скоррелированные оптические системы, которые лишь приближенно можно считать идеальными. Обычная сферическая линза далека от

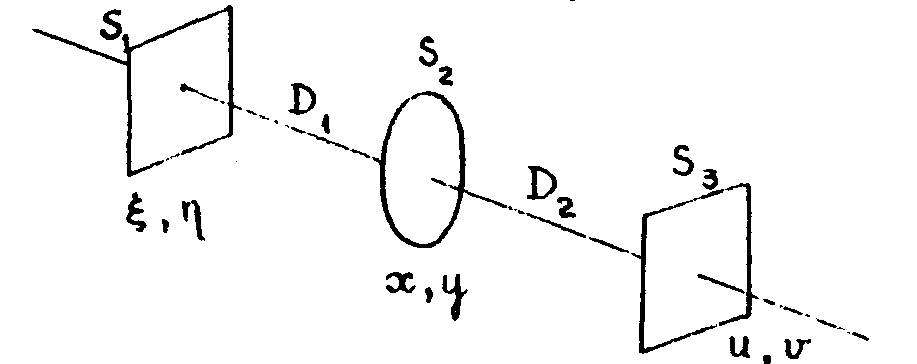
Рис.3. Распространение света и преобразование информации в свободном пространстве при наличии фокусирующей системы:

s₁ - транспарант, s₂ - фокусируюиот система, s₃ - экран.

идеальной. На эти необходимо всегда обращать внимание и подбирать соответствующую оптику, несмотря на то, что обычно на схемах изображаются простые линзы.

Наличие двух расстояний d₁ и d₂, которые свет проходит в свободном пространстве, приводит к двойному преобразованию Френеля:

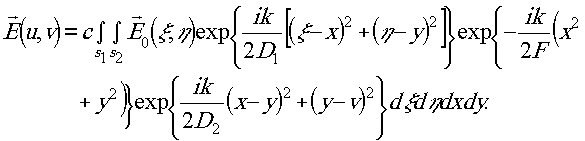
Если пренебречь в этой выражении членами, содержащими квадраты ξ и η, то получим , что 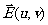будет представлено преобразованием Фурье-функции 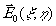. Условия, при которых преобразование Френеля переходит в преобразование Фурье, будут рассмотрены несколько позже. Здесь мы только отметим, не всегда такой переход делается обоснованно.

Написанное здесь двойное преобразование Френеля после одного интегрирования может быть представлено в следующем виде:

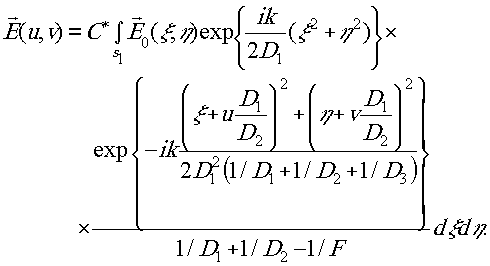
Теперь нетрудно видеть, что при Условии

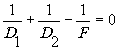
экспоненциальная функция под интегралом вместе со знаменателем превращается в δ -функцию. В результате этого получим следующее выражение:

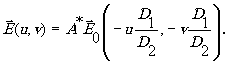
Теперь ясно, чти при выполнении соотношения 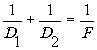на экране будет видно перевернутое изображение транспаранта с увеличением или уменьшением в зависимости от отношения d₁/d₂.

Только это положение оптической системы, которое мы сейчас с полным правом можем назвать частным случаем, использовались в течение более 100 лет в фотографии для записи, хранения и воспроизведения информации об окружающих нас предметах. Идея Габора как раз и заключалась в том, что в принципе имеются все основания для записи и воспроизведения информации при любом положении оптической системы или вовсе без неё.

д) Преобразование информации при различных видах дифракции

В оптике различают два вида дифракции: Френеля и Фраунгофера. Хотя оба эти вида хорошо известны, всё же следует сказать несколько слов по их поводу. Дифракция Френеля описывается формулой

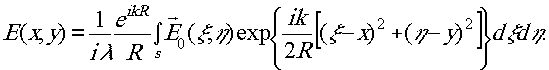
Эта формула списывает распределение амплитуд и фаз светового поля в точке, на положение которой наложены приведённые выше ограничения п.п.1-3. Преобразование, которое описывается этой формулой, носит так же, как и дифракция, имя Френеля.

В оптике рассматривают ещё и другой вид дифракции, которая носит название дифракции Фраунгофера и описывается формулой, представляющей собой преобразование Фурье.

При этом исходят из предположения, чти транспарант, на которой происходит дифракция, освещается точечный источникиу, находящийся от транспаранта на достаточно большом расстоянии, а дифракционная картина наблюдается "в бесконечности".

На основе не очень строгих рассуждений пренебрегают в показателе экспоненты квадратичными членами. В результате этого преобразование Френеля превращается в преобразование Фурье. Таким образом, дифракция Фраунгофера определяется в оптике как дифракция на бесконечно большом расстоянии вблизи нормали к поверхности

волнового фронта. Для голографии такое определение не подходит, так как при освещении транспаранта широким параллельным пучком света подобную аппроксимацию сделать нельзя. Действительно, представим расстояние r в фазовом множителе выражения для принципа Гюйгенса-Френеля следующим образом:

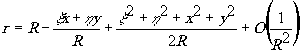
Ясно, что при r→∞ и неизменных величинах ξ, η, x, y, которые в голографии являются величинами одного и того к порядка малости, оба члена, содержащие r в знаменателе, будут стремиться к величинам одинакового порядка и пренебречь одним членом по сравнению с другим нельзя. Дифракция в свободном пространстве всегда остаётся дифракцией Френеля, если источник когерентного света неточечный.

Таким образом, иы приходим к следующий выводам.

Дифракция Френеля описывает дифракционную картину, возникающую при распространении света в свободном пространстве вблизи нормали к поверхности волнового фронта, на большом расстоянии от поверхности, создающей дифракцию. Информация об исходном изображении подвергается в этом случае преобразованию Френеля.

Дифракция Фраунгофера описывает дифракционную картину, полученную с помощью идеальной линзы или скоррелированной оптической системы, если расстояния между транспарантом и линзой,а также между линзой и экраном равны фокусному расстоянию линзы. Информация об изображении подвергается в этом случае преобразованию Фурье.

Действительно, рассмотрим приведённый выше пример. Двойное преобразование Френеля можно привести к такому виду:

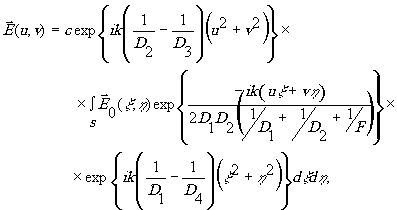
где

Нетрудно видеть, что если положить

d₁ = d₂ = f,

то квадратичные члены исчезнут и мы будем иметь преобразование Фурье в чистом виде. В других случаях отбрасывание квадратичных членов нужно производить с большой осторожностью.

ii. Классификация голограмм

Не случайно голограммы получили названия по типу дифракционной картины, которая содержит информацию об изображении предмета: голограммы Френеля, Фурье, Фраунгофера и т.д.; восстановленное изображение появляется благодаря дифракции. Таким образом, уже имеется классификация голограмм по типу дифракции, используемой при восстановлении. Представляется целесообразным дополнить эту классификацию и рассмотреть другие признаки, прямо или косвенно связанные с дифракцией.

По характеру регистрирующей среды голограммы, с одной стороны, могут быть разделены на толстослойные и тонкослойные, а с другой на амплитудные и фазовые^*. Толстослойные голограммы отличаются от тонкослойных тем, что несут дополнительную информацию о направлении распространения света и поэтому дают только одно восстановленное изображение. Тонкослойные голограммы имеют особенность, заставляющую вспомнить принцип Гюйгенса-Френеля в его первоначальном виде. Благодаря отсутствию информации о направлении света они дают два изображения, соответствующие двум возможным направлениям распространения волнового фронта от голограммы. Одно из этих изображений правильно отражает предмет, а другое является псевдоскопическим. Второе изображение может быть устранено,

как хорошо известно, только с помощью определённых дополнительных приёмов.

Свет при прохождении через голограмму (или при отражении от нее в случае некоторых видов голограмм) изменяет свою амплитуду и фазу. В соответствии с этим голограммы можно разделить на амплитудные и фазовые. Оснивным отличием амплитудных голограмм от фазовых является то, чти неоднородности, благодаря которым возникает дифракция, создаются в амплитудных голограммах за счёт поглощения или рассеяния света, в то время как в чисто фазовых голограммах поглощения света не происходит.

Разделение голлограми на амплитудные и фазовые носит до многих случаях условный характер потому, чти голограммы часто обладают способностью изменять одновременно как амплитуду, так и фазу падающего на них света.

Важной характеристикой голограммы является величина её дифракционной эффективности, которая показывает, сколько световой энергии поступает при восстановлении в первый породой дифракции (т.е. создаёт изображение).

Для чисто фазовых толстослойных голограмм величина дифракционной эффективности теоретически иожет доходить до 100%. Необходимо, однако, иметь в виду, что дифракционная эффективность толстослойных фазовых голограмм периодически изменяется с толщиной слоя и при определённых толщинах может стать равной нулю.

Кроме того, чисто фазовые голограммы обладают тем недостатком, что для них волна нулевого порядка, существовавшего при амплитудной записи, частично распределяется и на волны других порядков, из-за чего при восстановлении на изображении появляются блики, уменьшающие контраст. Это явление подробно описано в литературе.

Рассмотрим теперь классификацию тонкослойных голограмм по их дифракционным свойствам. Голограммы могут быть получены как без помощи оптических систем, так и с их помощью. Голограммы, получаемые без помощи оптических систем, можно классифицировать по характеру интерферограммы средней точки объекта. Рис.4 позволяет проиллюстрировать эту классификацию.

Из точки "А" на голограмму "Г" падает опорная волна. Ось "АБ"

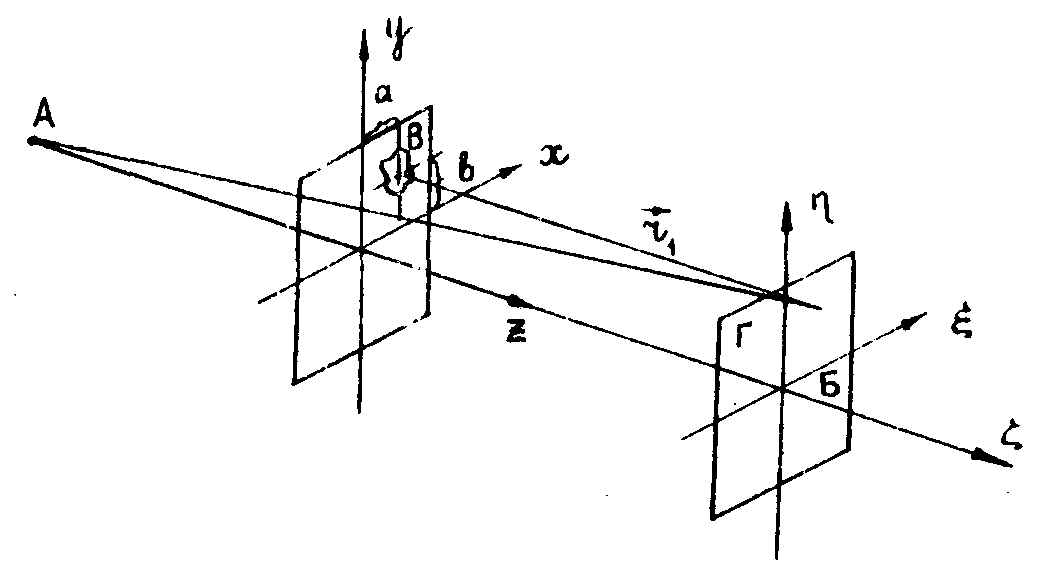
Рис.4. Схема записи голограммы (Г) предмета (В) при отсутствии фокусирующих систем.

является центральной осью этой волны. В точке с координатами x=а, y=b находится центр "В" голографируемого предмета. Предполагается, что голографируемый предмет освещается когерентным светом того же источника, что опорная волна. На рис.4. вектор 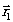показывает расстояние от центра голографируемого предмета до точки голограммы, не лежащей на оси "АБ". Вектор показывает расстояние от источника опорной волны до той же точки голограммы. Разность хода 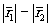определяется выражением

Накладывая определённые ограничения, из этого выражения можно получить три формы для разности хода, каждая из которых характеризует определённый вид голограммы.

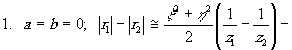
голограммы Френеля без несущей частоты (метод Габора).

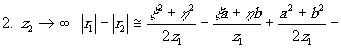
голограммы Френеля с несущей частотой (метод Лейта).

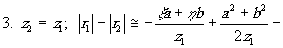
Голограммы Фурье по методу, расемотренному Строуком. Присутствие в последней формуле квадратичного члена, не зависящего от координат голограммы (определяемого положением точки на голографируемом предмете), указывает на то, что голограмма, полученная по этому методу, не является точным преобразованием Фурье.

С помощью фокусирующих оптических систем можно получить голограммы другого вида. Рассмотрим рис.5. Свет от предмета, прежде чем попасть на голограмму, проходит через оптическую систему. Кроме того, на голограмму падает свет опорного пучка, который обычно берётся параллельным. Можно взять и опорный пучок другого вида, но этот случай мы здесь рассматривать не будем.

Для такой схемы можно определить два частных случая, когда получаются голограммы определённого вида.

1. f₁=f₂=f -

голограмма Фурье на основе дифракции Фраунгофера (метод Лейта). Как было показано раньше, такое положение оптической системы даёт возможность получить преобразование Фурье в чистом виде.

2. 1/f₁+ 1/f₂ - 1/f = 0 -

голограмvа сфокусированного изображения. Раньше было показано,

что такое положение оптической системы даёт на экране, которым

в данном случае является голограмма, изображение предмета в

соответствующем масштабе.

Необходимо отметить, что описанную выше классификацию можно целиком распространить и на толстослойные голограммы. Формулы для разности хода 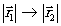действительно для двумерной плоскости остаются в силе, так как толстослойную голограмму можно рассматривать как состоящую из несольких тонких. Для голограым, получаемых по методу Ю.Н.Денисюка, необходимо лишь изменить положение опорного пучка так, чтобы он освещал противоположную сторону го-

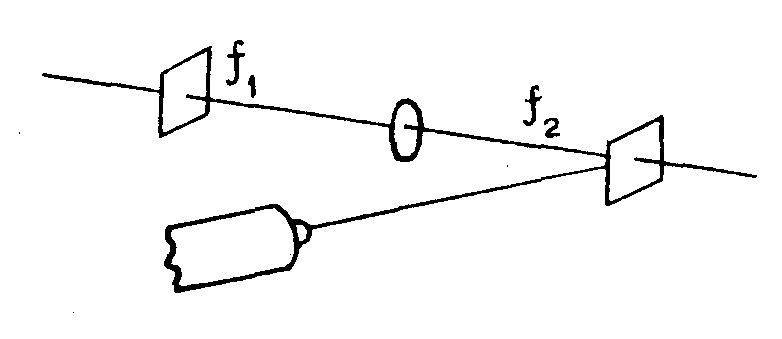
f₁=f₂=f - голограмма Фурье на основе дифракции Фраунгофера (метод Лейта);

1/f₁+ 1/f₂ - 1/f = 0 - голограмма сфокусированного изображения.

Рис.5. Схема записи голограммы при наличии фокусирующей системы.

лограммы. Эти достигается поворотом всего опорного пучка вокруг горизонтальной или вертикальной оси, проходящей через плоскость голограммы (ось ξ или η на рис.4).

iii. Некоторые особенности восстановления голограмм

Извлечение информации из голограммы имеет некоторые особенности, две из которых мы здесь рассмотрим.

Принято говорить, что голограмма содержит полную информацию о предмете. Однако, если предмет трёхмерный, полное представление о нём можно получить только рассматривая его со всех сторон, чего обычная плоская голограмма осуществить не позволяет. Для разъяснения этого обратимся к рис.6, на котором представлен процесс записи и воспроизведения информации с помощью голограммы. При восстановлении предмет отсутствует и голограмма освещается только опорной волной. Наблюдатель, перемещая точку наблюдения из положения 1 в положение 2, может рассмотреть детали изображения предмета, невидимые из положения 1, но весь предмет со всех сторон с помощью представленной на рис.6 голограммы он рассмотреть не может. Таким образом, наблюдатель имеет полную информацию только

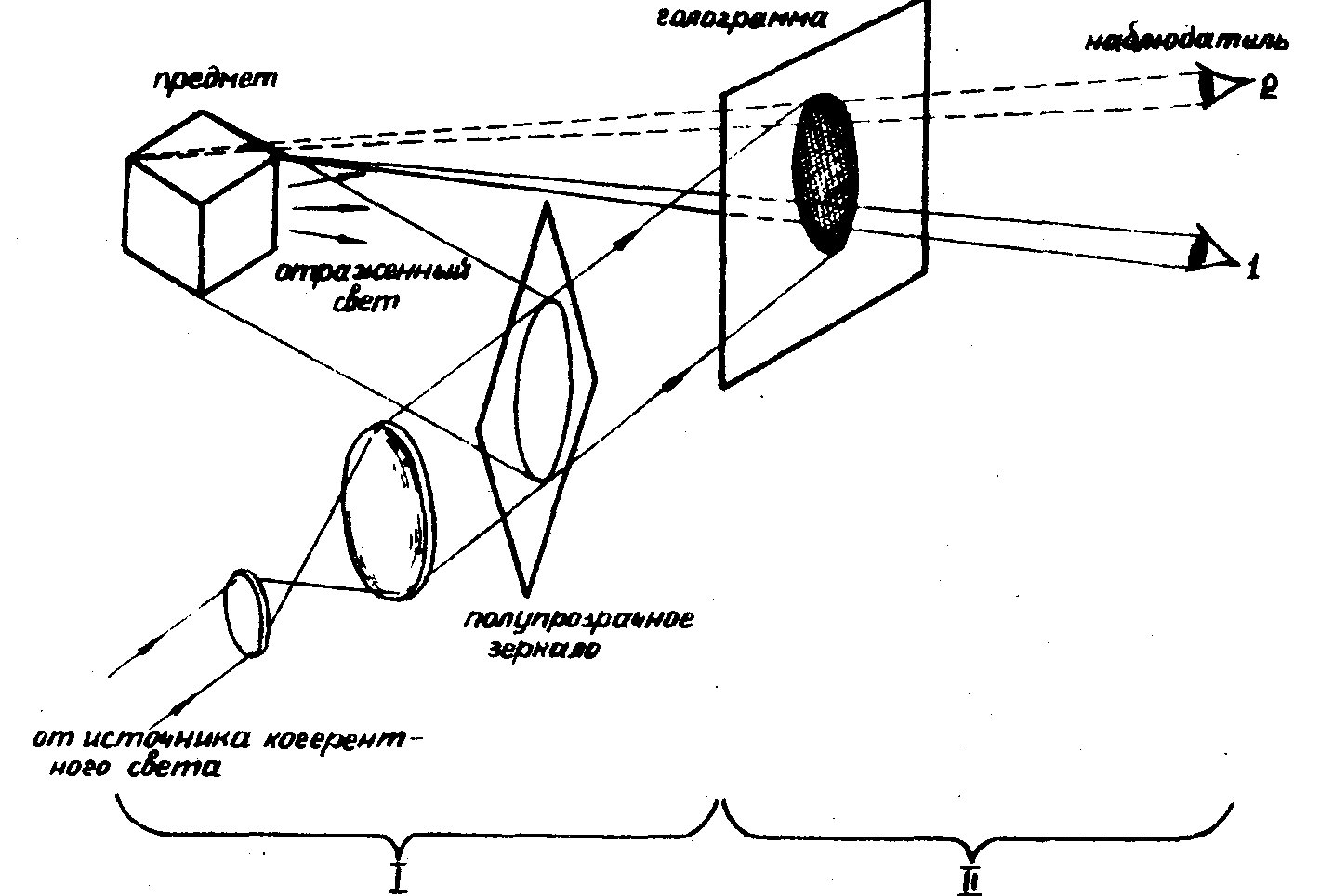
Рис.6. Схема, поясняющая запись голограммы и её восстановление.

о части предмета, а не о всём предмете. Информация, содержащаяся в голограмме, не является всей возможной информацией, которую может иметь о предмете наблюдатель. Поэтому необходимо делать различие между "Полной" информацией и "всей возможной" информацией. Хотя информацию, содержащуюся в голограмме и можно называть "полной" (потому что регистрируется как амплитуда, так и фаза волн, исходящих от предмета), однако количество информации зависит от размеров голограммы и "всю возможную" информацию (т.е. такую, которую может получить наблюдатель, рассматривая сам предмет, а не голограмму) практически зарегистрировать невозможно. Правда, существуют так называемые круговые голограммы, позволяющие значительно расширить объём информации, но и они не позволяют зарегистрировать полностью "всю возможную" информацию.

Другой особенностью голограмм является наличие в них информации, которую можно считать избыточной. Однако тонкослойные голограммы, например, имеют в то же время недостаток информации. Рассмотрим это подробнее.

Как известно, голограммы отличаются от стереоскопических фотографий наличием параллакса, благодаря которому при рассматривании голограммы возникает полная иллюзия нахождения предмета на том месте, на котором он помещался при голографировании.

Однако для того, чтобы получить представление о предмете, в большинстве случаев можно ограничиться небольшими величинами параллакса. Тогда можно считать, что голограмма, превышающая определённые размеры, будет содержать излишек информации.

С другой стороны, тонкослойные голограммы дают два изображения одного и того же предмета, что обусловлено отсутствием в таких голограммах информации о направлении распространения света.

Таким образом, голограмма может содержать излишек информации и одновременно в ней может быть недостаток информации. Разъяснение этого парадокса заключается в том, что излишек принадлежит к одному виду информации, а недостаток - к другому.