ГОЛОГРАФИЧЕСКИЕ СИСТЕМЫ
ДЛЯ ИЗМЕРЕНИЯ ЛИНЕЙНЫХ ПЕРЕМЕЩЕНИЙ
И ФАЗОВЫХ СДВИГОВ
Б.Г.Турухано, Н.Турухано
Рассмотрены когерентные
измерительные системы, основанные на комбинации интерференционного
поля и голографической дифракционной решётки. Проведены
исследования одно- и двухкоординатных измерительных систем.
Показано, что введение подвижной согласованной дифракционной
реиётки в двухлучевой интерферометр позволяет измерять сдвиг
фазы световой волны. Предложенные системы
удобны при
автоматическом отсчёте линейных перемещений и сдвига фазы
световой волны, а также имеют ряд преимуществ перед некогерентными
измерительными системами.
Развитие когерентной оптики и голографии открывает
возможность создания когерентных устройств для точного измерения
линейных перемещений и фазы световой волны, имеющих ряд преимуществ
перед некогерентными измерительными системами /1,2/. В настоящей
работе рассматриваются когерентные измерительные системы,
основанные на комбинации согласованного и рассогласованного
интерференционного светового поля скрещенных пучков с синусоидальной
дифракционной решёткой /1/. Ведём определение согласованного
и рассогласованного интерференционного поля с синусоидальной
дифракционной решёткой. Будем называть интерференционное поле
согласованным с синусоидальной дифракционной решёткой, когда
период и направление интерференционных линий поля и полос
решётки совпадают, а рассогласованным, когда период или направление
линий поля и полос решётки не совпадают.
- Согласованное интерференционное поле
с синусоидальной дифракционной
решеткой
При взаимодействии двух когерентных коллимированных
пучков света длиной волны λ, падающих на фотопластинку
под углами ±θ/2 к нормали последней, перед фотопластинкой
и в зоне пересечения пучков возникает интерференционное поле,
как показано на рис.1. Волны пучков в сечении вдоль оси х
можно записать в виде
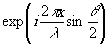 и
и 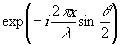 ,
,
если амплитуды пучков принять за единицу и
не учитывать временную часть волны в силу когерентности источника.
В этом случае распределение интенсивности интерференционного
поля в плоскости фотопластинки можно записать как
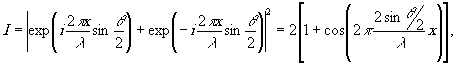 (1)
(1)
откуда следует, что распределение интенсивности
интерференционного поля вдоль оси х подчиняется синусоидальному
закону с частотой
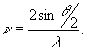 (2)
(2)
Если фотопластинка
обладает необходимой разрешающей способностью и коэффициентом
контраста γ, равным -2, то почернение фотопластинки будет
пропорционально интенсивности интерференционного поля, определяемого
выражением (1). Заметим, что таким методом и создаются синусоидальные
голографические дифракционные решётки, которые не дают спектрального
разложения выше
±1 порядка в силу своей синусоидальности.
Так как фотопластинка негативная, ярким зонам
поля будут соответствовать темные участки фотопластинки. При
этом детектор 3 (pиc.1) будет показывать минимальное значение
светового потока. Для получения максимального светового потока
необходимо сдвинуть фотопластинку на величину, равную половине
периода дифракционной
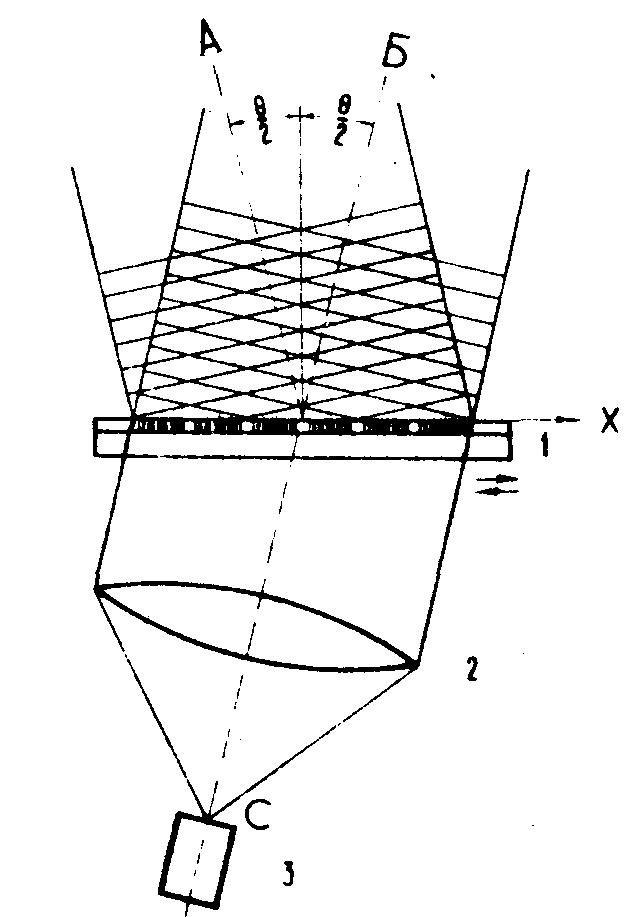
Рис.1. Голографичеекая дифракционная
решётка в согласованном интерференционном поле:
1 - голографическая дифракционная
решётка,
2 - линза; 3 - детектор.
решётки 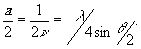 При дальнейшем смещении фотопластинки вдоль оси х световой
поток будет менять свою интенсивность в соответствии с шагом
дифракционной решётки. Таким образом, комбинация согласованного
интерференционного поля и синусоидальной дифракционной решётки
может служить для измерения линейного перемещения решётки
относительно поля.
При дальнейшем смещении фотопластинки вдоль оси х световой
поток будет менять свою интенсивность в соответствии с шагом
дифракционной решётки. Таким образом, комбинация согласованного
интерференционного поля и синусоидальной дифракционной решётки
может служить для измерения линейного перемещения решётки
относительно поля.
Однако в этом случае световой поток не содержит
информацию о направлении движения решётки. Для получения этой
информации необходимо использовать комбинацию рассогласованного
поля относительно дифракционной решётки. Причём рассогласование
может быть либо по частоте интерференционных линий поля и
полос решётки, либо по направлению линий поля и полос дифракционной
решётки. В первом
случае возникают обтюрационные полосы, во
втором - муаровые полосы по аналогии о системой двух дифракционных
решёток /3/.
2. Рассогласованное
интерференционное поле с синусоидальной дифракционной решёткой
Если дифракционная
решётка выполнена по оптической схеме 1, то частота её определяется
выражением (2). Для рассогласования интерференционного поля
по частоте относительно дифракционной решетки отклоним каждый
пучок ещё на угол δ, как показано на рис.2. При взаимодействии
отклоненных пучков с решеткой за решёткой слева образуется
нулевой порядок пучка 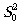 и первый порядок пучка
и первый порядок пучка 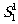 ,
идущий под углом Ψ к нормали. По условию Брегга угол
Ψ связан с углом падения пучка на дифракционную решётку
,
идущий под углом Ψ к нормали. По условию Брегга угол
Ψ связан с углом падения пучка на дифракционную решётку
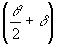 как
как
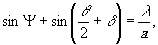 (3)
(3)
где а - постоянная дифракционной решётки.
Рассмотрим взаимодействие
двух пучков 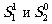 .
Их суммарная интенсивность, если принять их амплитудные части
волн за единицу, выразится следующим образом:
.
Их суммарная интенсивность, если принять их амплитудные части
волн за единицу, выразится следующим образом:
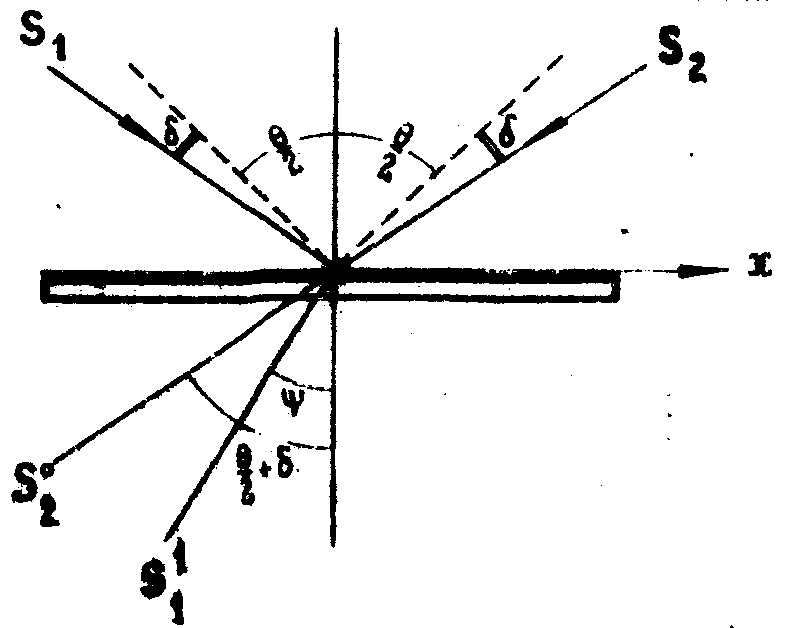
Рис.2. Оптическая схема получении
остюрационных полос.
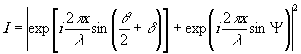
или (4)
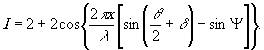
Выражение (4) показывает, что интенсивность
обтюрационных полос изменяется по синусоидальному закону вдоль
оси х, а частота полос определяется выражением
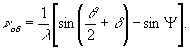 (5)
(5)
Учитывая условие Брегга
(3) и что постоянная решетки 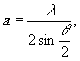 получим
получим
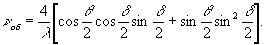 (6)
(6)
Рассмотрим образование
муаровых полос при рассогласовании направления интерференционных
линий поля и штрихов дифракционной решётки. Пусть полученная
фотографическим способом синусоидальная дифракционная решётка
после изготовления будет повёрнута на угол φ вокруг центрального
пучка s1o,
как показано на рис.3. В результате взаимодействия интерференционного
поля с повернутой дифракционной решёткой после решётки возникнут
муаровые полосы. Их можно рассматривать как интерференцию
двух пучков 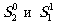 .
Пучок
.
Пучок 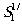 образуется как первый порядок дифракции пучка s1
на повёрнутой дифракционной решётке 2(рис.3). Через волновые
функции пучков можно определить частоту муаровых полос, как
это было сдедано для обтюрационных полос. Однако можно, рассмотрев
интерференцию коллимированных пучков
образуется как первый порядок дифракции пучка s1
на повёрнутой дифракционной решётке 2(рис.3). Через волновые
функции пучков можно определить частоту муаровых полос, как
это было сдедано для обтюрационных полос. Однако можно, рассмотрев
интерференцию коллимированных пучков 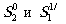 ,
сходящихся под углом на решётку, сразу записать частоту интерференционных
муаровых полос, направленных параллельно биссектрисе угла
φ, согласно выражению (2),
,
сходящихся под углом на решётку, сразу записать частоту интерференционных
муаровых полос, направленных параллельно биссектрисе угла
φ, согласно выражению (2),
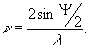
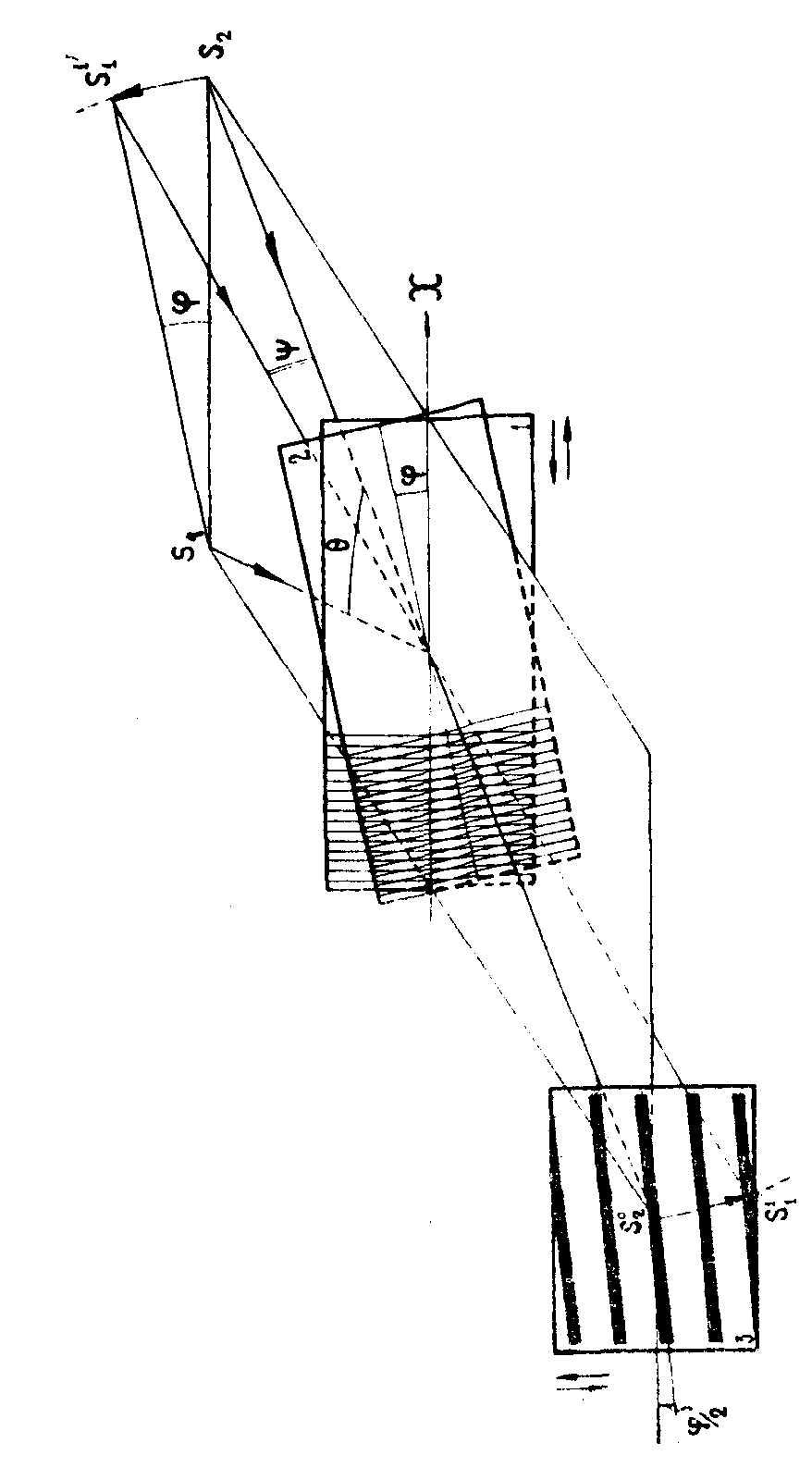
Затем на геометрических соотношений (рис.3)
выразить угол Ψ через θ и φ
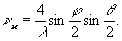 (7)
(7)
Практически интересен случай малых рассогласований,
т.е. случай широких муаровых и обтюрационных полос. Для малых
рассогласований θ и φ можно переписать выражения
(7) и (б) в виде

откуда видно, что для малых рассогласований
частота муаровых и обтюрационных полос линейно связана с углами
рассогласования.
Резюмируя изложенное,
можно отметить, что комбинация рассогласованного интерференционного
поля и дифракционной решётки может служить для определения
линейного перемещения решётки относительно поля. При этом
смещение решётки на шаг вдоль оси х будет соответствовать
смещению на шаг муаровых и обтюрационных полос. Направление
движения решётки относительно поля связано с направлением
движения муаровых и обтюрационных полос. Так, при движении
дифракционной решётки вправо и влево (рис.3) муаровые полосы
будут перемещаться вверх и вниз, а обтюрационные полосы (рис.2)
вправо и влево, чего не наблюдалось при движении решётки в
согласованном поле, которое можно считать
частным случаем рассогласованного поля и решётки, когда частоты
- νм и νоб равны нулю.
3. Исследование
свойств системы: голографическая синусоидальная решётка -
интерференционное поле
Для изучения взаимодействия согласованного
и рассогласованного интерференционных полей с дифракционной
решёткой была создана установка, схема которой приведена на
рис.4. Оптическая часть установки использовалась при изготовлении
дифракционных решёток
высокого контраста. При этом для увеличения
пространственной когерентности и получения однородного светового
поля луч одномодового гелий-неонового лазера фокусировался
на диафрагму 3 с отверстием 36 мкм. Для устранения вибраций
установка помещалась на бетонный куб, развязанный от фундамента.
Вибрации установки контролировались методом, описанным в /4/.
Перечисленные особенности установки позволяли получать высококонтрастные
голографические дифракционные решётки с частотой более 3000
линий на миллиметр на фотопластинках СРБШ ИАЭ-1.
Для получения обтюрационных полос частота
интерференционных линий поля изменялась поворотом зеркал (6
и 9 на рис.4). При наблюдении муаровых полос изменялся наклон
линий дифракционной решётки относительно интерференционных
линий поля за счёт поворота решетки.
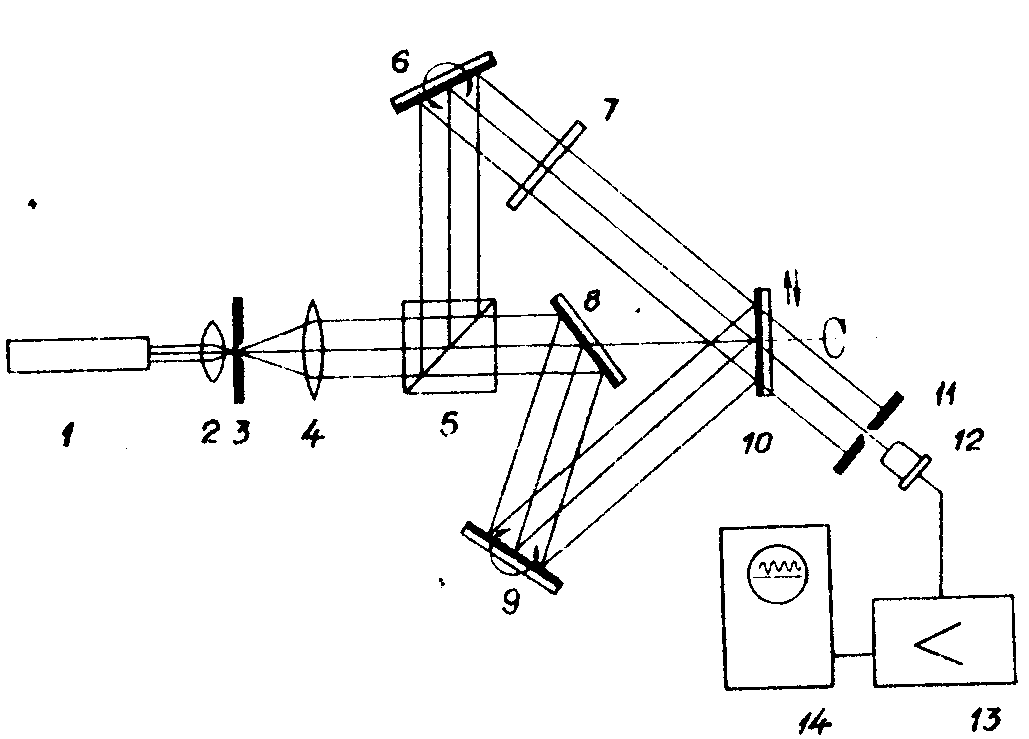
Рис.4. Схема установки для изучения
взаимодействия интерференционного поля с дифракционной
решеткой:
1 - лазер; 2,4 - коллиматор; 3
- круглая диафрагма;
5 - призма-куб, 6,8,9 - зеркала
интерферометра; 7 -светофильтр; 10 - дифракционная
решётка; 11 - щелевая диафрагма; 12 - детектор;
13 - усилитель; 14 -осциллограф.
Для получения максимально
контрастных обтюрационных и муаровых полос после изготовления
дифракционной решётки в один из пучков устанавливался светофильтр
7, который уравнивал интенсивности интерферирующих пучков
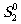 и
и 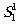 (рис.2) при получении обтюрационных полос и пучков
(рис.2) при получении обтюрационных полос и пучков
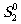 и
и 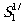 (рис.3) при получении муаровых полос. На рис.5 б,в приведены
фотографии муаровых полос, полученных с голографическими дифракционными
решётками, частота которых была 1000 и 3000 лин./мм. Понижение
контраста муаровых полос при частоте решётки в 3000 лин./мм
объясняется спадом Ч К Х использованных фотопластинок при
частоте 3000 лин./мм.
(рис.3) при получении муаровых полос. На рис.5 б,в приведены
фотографии муаровых полос, полученных с голографическими дифракционными
решётками, частота которых была 1000 и 3000 лин./мм. Понижение
контраста муаровых полос при частоте решётки в 3000 лин./мм
объясняется спадом Ч К Х использованных фотопластинок при
частоте 3000 лин./мм.
На рис.5 г,д показан
периодический сигнал на детекторе (12 на рис.4), воспринимающем
интенсивность муаровой полосы при движении дифракционной решётки,
перед детектором (фотодиод ФД-3) располагалась щель 11, параллельная
муаровой полосе и шириной 0,2 полосы. Глубина модуляции фотоэлектрического
сигнала, снимаемого с осциллографа 14, падает с увеличением
частоты дифракционной решётки в силу понижения её контраста.
Так, для решёток в сотни линий на миллиметр глубина модуляции
достигает 100%, для решёток 100 лин./мм
составляет
80÷90% и
для решёток 3000 лин./мм падает до 50÷60%.
Для обтюрационных полос получены аналогичные картины и кривые
модуляции.
Голографические дифракционные решётки можно
заменить обычными нарезными фазовыми или отражательными решётками.
Фотография муаровых полос от фазовой нарезной решётки с частотой
100 лин./мм, помещённой в интерференционное поле, показана
на рис.5а. Так как нарезные решётки несинусоидальны, они дают
спектральные порядки выше первого, и частота муаровых и обтюрационных
полос определяется индексами интерферирующих порядков /5/.
Распределение интенсивности муаровых и обтюрационных полос
также в силу несинусоидальности решётки будет определяться
формой штрихов, что видно из рис.5а.

Рис.5. Фотографии муаровых полос (а,б,в)
и осциллограммы фотоэлектрических сигналов от муаровых
полос при движении голографических дифракционных решёток
в 1000 и 5000 лин./мм (г,д).
Прямые линии показывают уровень раавёртки
при отсутствии сигнала на детекторе.
4. Оптические
схемы датчиков линейных перемещений, основанные на голографических
принципах
Цена муаровых и обтюрационных
полос определяется шагом дифракционной решётки, который может
варьироваться в широких пределах изменением угла θ и
длины волны используемого излучения λ. В связи с этим
рассмотренные датчики можно условно разбить на три типа в
зависимости от способа получения интерференционного поля скрещенных
пучков:
1) низкочастотные, использующие голографические
или нарезные дифракционные решётки с частотой до 100 лин./мм;
2) среднечастотные с нарезными или голографическими
решётками с частотой до 100 лин./мм;
3) высокочастотные с голографическими решётками
в несколько тысяч лин./мм.
На рис.6а,б,в приведены оптические схемы для
всех трёх типов датчиков, общим для всех трёх схем может служить
источник-лазер-1, система расширения и коллимации пучка -
2,3,4, наличие двухлучевого интерферометра - 5, подвижной
дифракционной решётки - 6 и приёмной фотоголовки. Для низкочастотного
датчика (рис.6а) в качестве формирователя скрещенных пучков
удобно использовать призму-куб со скошенной гранью-5, грани
а,б имеют зеркальное покрытие.
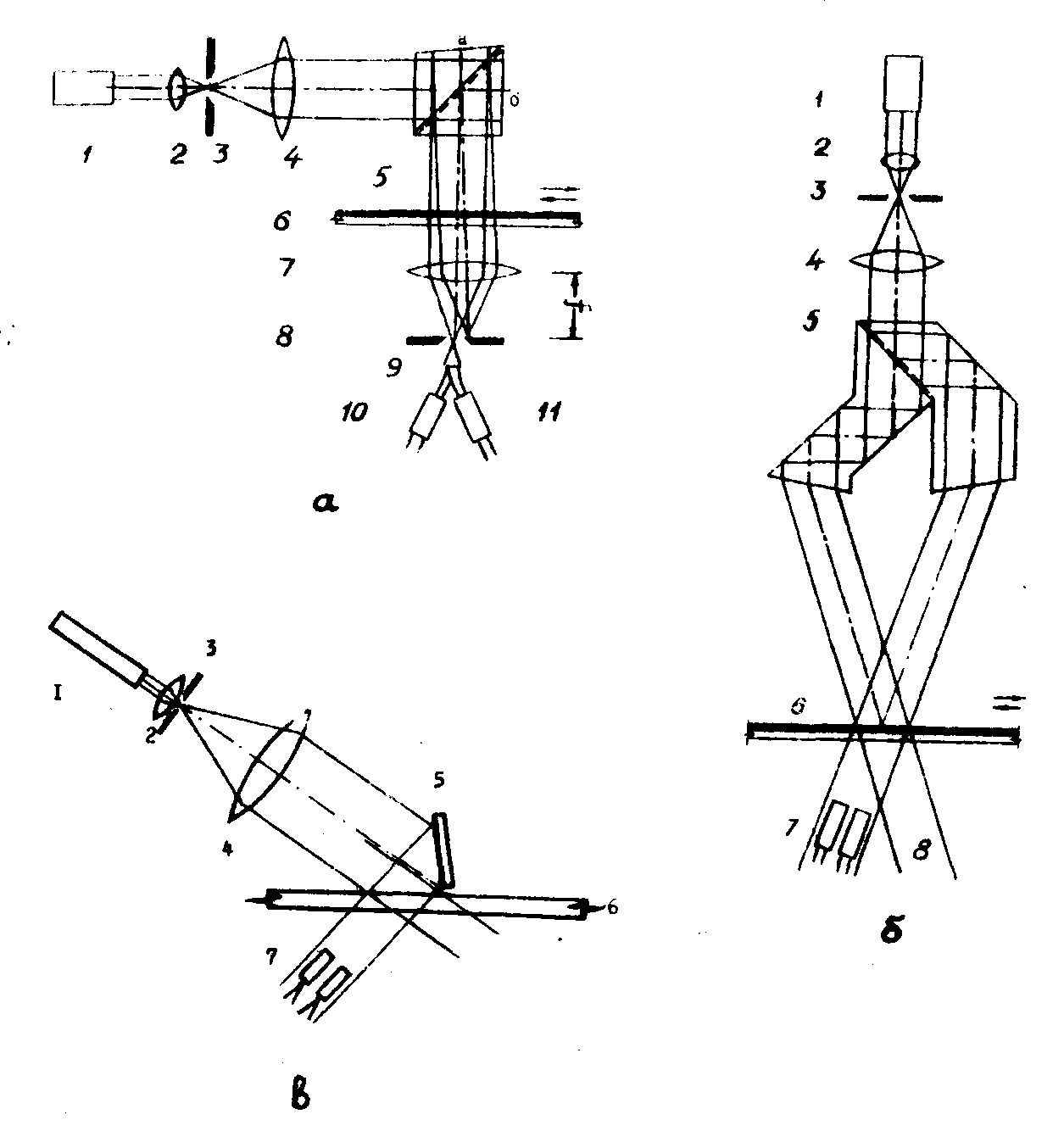
Рис.6. Оптические схемы датчиков линейных
перемещении:
- 4 - лазер с системой формирования коллимированного
пучка; 5 - оптический элемент формирования скрещенных пучков;
6 - измерительная дифракционная решетка; 7-10 - фоторегистрирующая
часть датчика.
Для того, чтобы пучки
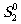 и
и 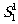 не перекрывались с пучками
не перекрывались с пучками 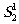 ,
,
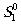 ,
, 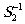 и
и 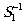 ,
за дифракционной решёткой находится линза 7 с диафрагмой 8,
которая устанавливается в фокусе линзы и задерживает свет
от паразитных пучков. Аналогичный результат можно получить,
удалив детектор 9 на такое расстояние, после которого пучки
естественно расходятся.
,
за дифракционной решёткой находится линза 7 с диафрагмой 8,
которая устанавливается в фокусе линзы и задерживает свет
от паразитных пучков. Аналогичный результат можно получить,
удалив детектор 9 на такое расстояние, после которого пучки
естественно расходятся.
В среднечастотном датчике (рис.6б) для формирования
скрещенных пучков использована специальная призма 5, предложенная
в работе /6/.
Для высокочастотного датчика можно пользоваться
оптической схемой, приведённой на рис.4, либо более простой
схемой (рис.6в), которая требует, однако, источника высокой
когерентности.
Рассмотренные измерительные системы просты,
удобны в настройке и не требуют таких точных механических
элементов, как система скрещенных дифракционных решеток /2,3,5,7/.
5. Двухкоординатный
датчик линейных перемещений
Рассмотренные системы позволяют производить
измерение линейного перемещения лишь по одной координате.
Поэтому при измерении двух координат необходимо иметь два
таких устройства и механически их связывать.
Используя уникальные возможности голографии
при изготовлении дифракционных решёток сложной конфигурации,
можно получить голографическую дифракционную решётку со взаимно
ортогональными штрихами. При этом необходимо использовать
уже не два, а три скрещенных пучка когерентного света. Для
этой цели использовался трёхлучевой интерферометр, представленный
на рис.7.
Работа интерферометра происходит следующим
образом. Коллимированный пучок лазерного света падает на светоделящую
пластину 4. Прошедший луч падает на вторую светоделящую пластину
6, а отражённый луч направляется зеркалом 5 на голограмму
8. Отражённый пластиной 6 луч направляется зеркалом 7 на голограмму,
куда приходит и прошедший луч. Отметим, что лучи, отражённые
полупрозрачными зеркалами 4 и 6, направлены под углом π/2
друг к другу
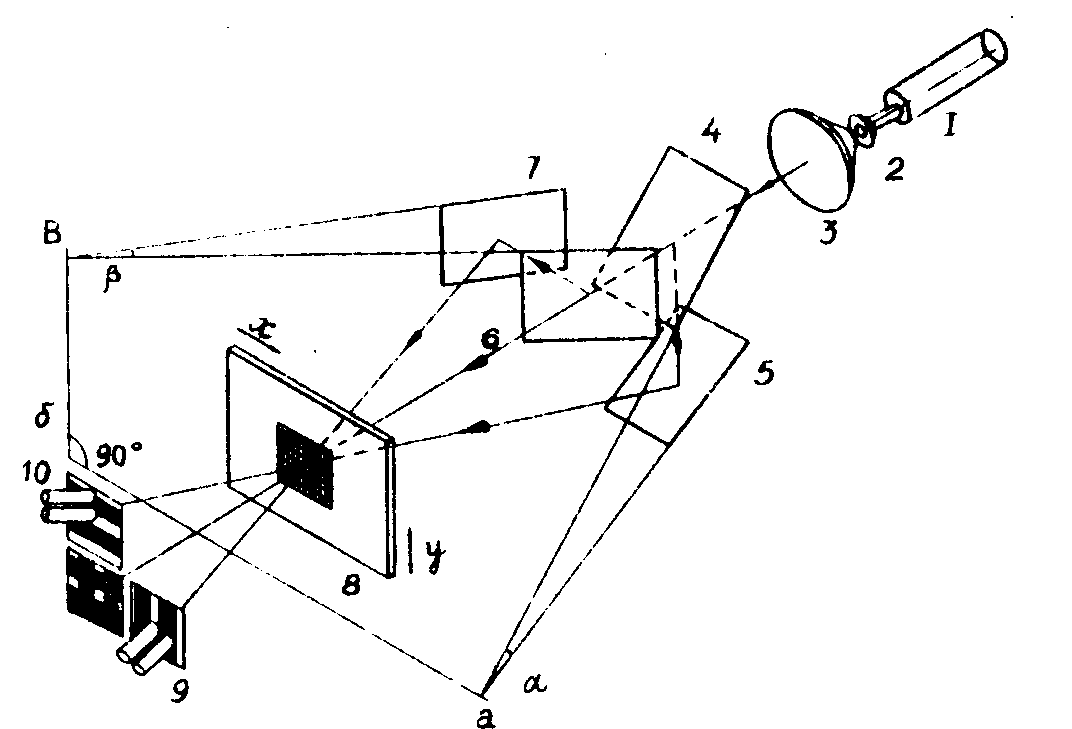
Рис.7. Оптическая схема двухкоординатного
датчика линейных перемещений:
1-3 - лазер и коллимирующая оптика;
4,6 -полупрозрачные зеркала; 5,7 - зеркала; 8 -голограмма;
9 - фотоприёмные устройства.
и к оси системы. Таким образом, на голограмму
приходят три коллимированных пучка, которые создают интерференционное
поле с ортогональными интерференционными полосами.
При засветке фотопластинки получим голографическую
дифракционную решётку с ортогональными штрихами. При рассогласовании
интерференционного поля относительно дифракционной решётки
по углу либо по частоте образуются соответственно муаровые
и обтюрационные полосы, частоты которых определяются выражениями
(7 и 6).
На рис.7 позиции 9 и 10 указывают обтюрационные
полосы. При движении голограммы вдоль направления х полосы
побегут перед фотодатчиками 9, а перед фотодатчиками 10 будут
неподвижны. При смещении голограммы вдоль направления у получим
обратную картину.
Согласно рассмотренной оптической схеме был
собран макет двухкоординатного датчика чинсйных перемещений.
Частота решётки по
обоим направлениям
была выбрана 300
лин./мм. На рис.6 показана фотография муаровых полос за дифракционной
решёткой после её незначительного поворота в интерференционном
поле. Существенно отметить, что имеются поля, где муаровые
полосы отвечают лишь одному направлению перемещения (б,в)
и есть поле, где имеется перекрестная модуляция х и у направлений
(г).

Рис.8. Фотография муаровых полос за
голографической дифракционной решёткой с ортогональными
штрихами:
а - поле пучка нулевого порядка;
б,в - поля пучков первого порядка;
г - поле перекрёстной модуляции от
пучков первого порядка
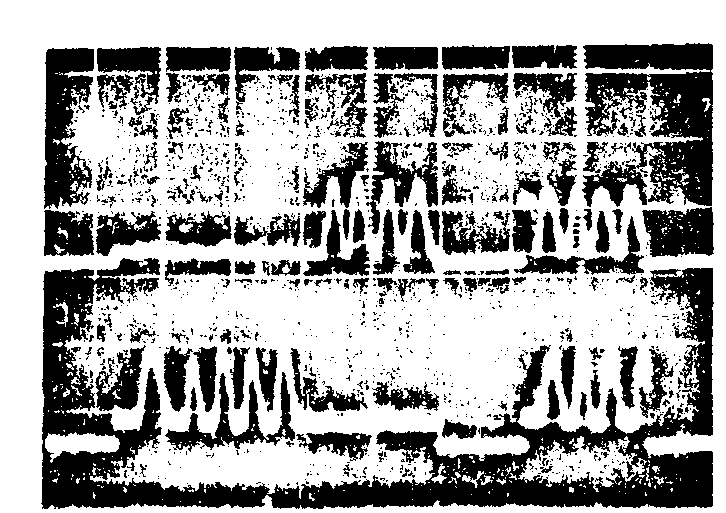
Рис.9. Осциллограммы электрических импульсов,
генерируемых фотодатчиками при смещении решетки по х и
у направлениям.
На рис.9 приводятся фотоэлектрические сигналы,
снятые с двухлучевого осциллографа. Осциллограммы показывают,
что движение по одному направлению вносит незначительный шум
при записи счётных импульсов другого направления.
6. Особенности
голографических датчиков линейных перемещений
Отметим особенности когерентных измерительных
систем основанных на комбинации интерференционного поля и
дифракционной решётки. Голографические дифракционные решетки
могут иметь частоты более 3000 лин./мм при использовании гелий-неонового
лазера. Если приёмная фотоголовка измерительной системы может
контролировать часть полосы /7/, точность отсчёта линейного
перемещения может достигать сотых долей микрона. Цена муаровых
и обтюрационных полос определяется шагом дифракционной решётки,
который может варьироваться в широких пределах изменением
угла θ и длины волны используемого излучения λ (см.
выражение (2) ). Здесь необходимо отметить, что точность интерференционных
измерительных систем определяется не ценой муаровой полосы,
а такими параметрами квантового генератора, как стабильность
мощности, длины волны и т.п., и также связана с рядом характеристик
(ЧКХ, ДЭ) используемой дифракционной решётки.
Описанные выше измерительные системы просты
и удобны в настройке и не требуют таких точных механических
элементов, как система скрещенных дифракционных решёток /3,5,7/.
В системе автоматического измерения линейного перемещения
данные системы могут работать при наличии значительных вибраций.
Вибростойкость установки необходима лишь на стадии изготовления
голографической дифракционной решётки. При работе измерительной
системы в условиях вибрации необходимо выполнить два требования:
во-первых, сохранять неизменным угол θ между пучками
и, во-вторых, частоты вибрации должны укладываться в частотную
полосу фотоэлектрической системы. Первое требование выполняется
выбором жёсткой конструкции интерферометра. Удобной конструкцией
интерферометра может служить призма-куб со скошенной гранью
(рис.6а) и специаль-
ная призма (рис.6б) /6/.
Приёмная фотоголовка
может располагаться на значительном удалении от измерительного
звена, так как протяжённость поля муаровых и обтюрационных
полос при использовании гелий-неонового лазepa
составляет несколько метров. При этом решётка может быть помещена
в любой области интерференционного поля.
Использование голографических дифракционных
решёток сложного профиля позволяет вести одновременное измерение
двух координат как в ортогональной, так и в косоугольных проекциях.
Объединение двух измерительных узлов в один с использованием
одного измерительного элемента повышает точность и надёжность
измерений.
Пропускание оптической
системы при использовании фазовых голографических дифракционных
решёток достигает 30-40%.
7. Измерение фазового сдвига
световой волны подвижной голографической дифракционной решёткой
При измерении показателя преломления веществ,
различных оптических неоднородностей, малых толщин необходимо
знать смещение пространственной фазы световой волны. Это смещение
с высокой степенью точности можно определить с помощью подвижной
согласованной голографической дифракционной решётки, помещённой
в двухлучевой интерферометр Релея.
Рассмотрим работу интерферометра
Релея с согласованной синусоидальной дифракционной решёткой.
Схема интерферометра представлена на рис.10. Пусть согласованная
синусоидальная решётка выполнена, как описано в пункте первом,
где вводится понятие согласованной решётки с интерференционным
полем. Падающие на решётку
лучи s1
и s2,
будут разлагаться решёткой каждый на 3 луча: 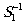 ,
,
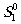 ,
, 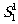 и
и 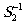 ,
,
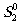 ,
, 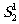 . В силу согласованности решётки и поля пучков s1
и s2
лучи
. В силу согласованности решётки и поля пучков s1
и s2
лучи 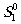 и
и 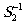 будут распространяться
за решёткой соосно, так же, как и лучи
будут распространяться
за решёткой соосно, так же, как и лучи
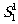 и
и 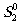 .
Найдём изменение фазы лучей
.
Найдём изменение фазы лучей 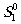 и
и 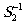 при сдвиге решётки
на величину Δx.
при сдвиге решётки
на величину Δx.
Запишем волны s1
и s2 в
виде
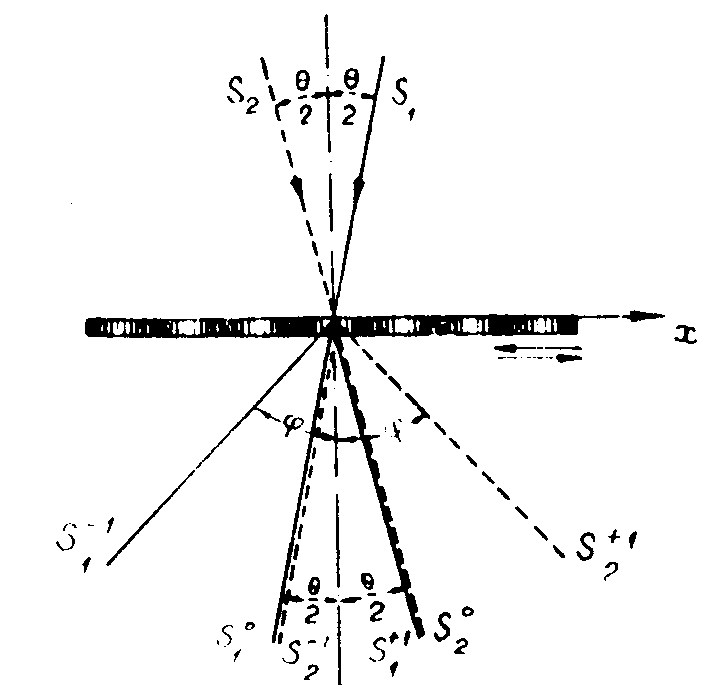
Рис.10. Схема согласованного интерферометра
Релея.
s1=eiωx,
s2=e-iωx,
(10)
где
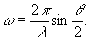
Амплитуды волн примем
за единицу. Тогда пропускание фотопластинки при выборе γ=2
запишется в виде
t=s1+s22=2+e2iωx+e-2iωx.
(11)
При смещении фотопластинки
на Δx
получим
tΔx=2e2iω(x+Δx)+e-2iω(x+Δx)
(12)
При дифракции волн
s1
и s2
на смещенной дифракционной решётке с пропусканием tΔx,
получим волны:
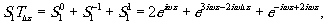 (13)
(13)
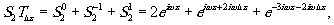 (14)
(14)
Выберем из выражений (13) и (14) волны, идущие
по одному направлению, т.е. интерферирующие за фотопластинкой:
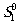 и
и 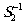 :
:
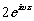 и
и 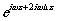 (15)
(15)
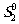 и
и 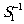 :
:
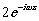 и
и 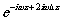 (16)
(16)
Будем далее рассматривать
две волны 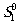 и
и 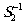 .
Заметим следующую особенность: при сдвиге дифракционной решётки
на Δх волна
.
Заметим следующую особенность: при сдвиге дифракционной решётки
на Δх волна 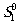 не получает приращения
по фазе, а волна
не получает приращения
по фазе, а волна 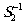 получает приращение по фазе 2ωΔυ. Подставив
значение ω, получим
получает приращение по фазе 2ωΔυ. Подставив
значение ω, получим
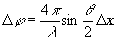 (17)
(17)
Резюмируя изложенное,
можно отметить, что смещением решётки можно по линейному закону
менять сдвиг фазы в пучке 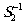 ,
а пучок
,
а пучок 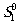 не
получает при этом никакого фазового сдвига. Это явление и
лежит в основе измерения разового сдвига.
не
получает при этом никакого фазового сдвига. Это явление и
лежит в основе измерения разового сдвига.
Схема прибора для
измерения фазового сдвига показана на рисунке 11. Два коллимированных
пучка s1
и s2
и подвижная дифракционная решётка 10 создают интерферометр
Релея. За решёткой используются пучки
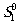 и
и
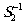 .
Объектив 11 репроецирует исследуемый фазовый объект 9 на экран
12.
.
Объектив 11 репроецирует исследуемый фазовый объект 9 на экран
12.
Для измерения фазового
сдвига интерферометр без образца движением согласованной решётки
настраивается на тёмное (либо светлое) поле, регистрируемое
на экране 12. После внесения образца с фазовым сдвигом Δφ
δифракционная решётка смещается и компенсирует вносимый
образцом сдвиг фазы. По величине смещения решётки Δх
рассчитывается фазовый сдвиг Δφ.
Аналитически эту процедуру
можно записать следующим образом. Пучок
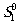 получит
фазовый сдвиг от образца,
получит
фазовый сдвиг от образца, 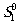 =eiωx-iωφ,
=eiωx-iωφ,
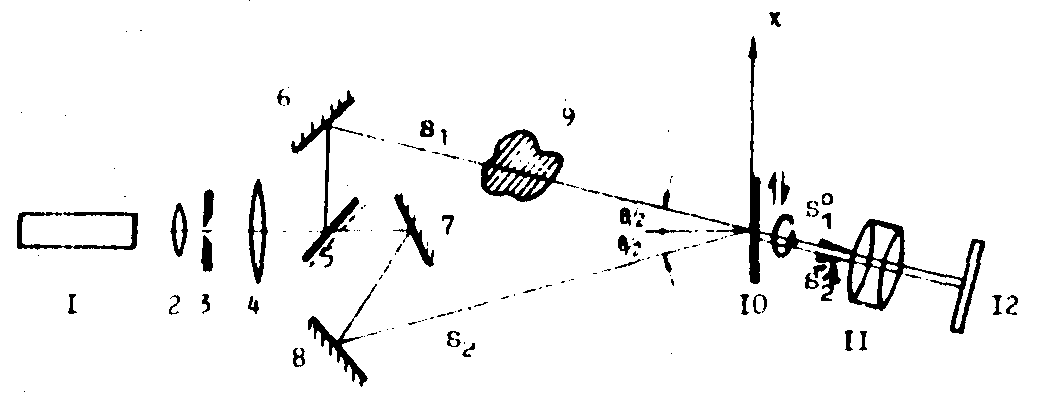
Рис.11. Оптическая схема прибора для
измерения фазового сдвига:
1 - лазер,
2-4 - коллиматор, 5-8 - зеркала двухлучевого интерферометра,
9 - фазовый объект, 10
- подвижная решетка, 11 - проекционный осбъектив,
12 - экран.
а пучок 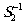 получит фазовый сдвиг при смещении решетки,
получит фазовый сдвиг при смещении решетки,
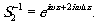
На экране регистрируется интенсивность интерференционной
картины:
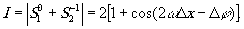 (18)
(18)
При настройке интерферометра на темное (светлое)
поле находится экстремальное значение интенсивности интерференционного
поля на экране, т.е.
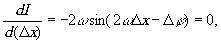 (19)
(19)
откуда
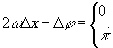 (20)
(20)
После подстановки значения ω получим
выражения для фазового
сдвига.
1. Интерферометр, настроенный на тёмное поле,
после внесения
образца вновь настраивается на тёмное поле:
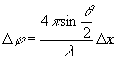 (21)
(21)
2. При настройке на светлое поле получим
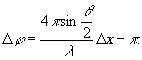 (22)
(22)
Для экспериментальной
проверки метода было использовано два фильтра из слюды. Один
фильтр соответствовал красному цвету (λ = 0,63), второй
зелёному (λ= 0,54). На рис.12 (а,б,в) приведены фотографии
освещённости при различных смещениях согласованной решётки,
получаемых на экране 12. На рис.15 приведены графики изменения
освещённости в зависимости от смещения решётки: жирная кривая
- поле без фильтров, тонкая - красный фильтр, пунктирная -зелёный
фильтр. Фазовые сдвиги, рассчитанные по минимуму освещенности.для
красного фильтра Δφ1=119,8°,
для зелёного Δφ2=204°.

Рис.12. Изменение интенсивности интерференционного
поля при смещении решётки (а,б,в) и возникновение интерференционных
полос при повороте решётки (г,д,е):
1- поле фильтра толщиной 0,65 мкм,
2 - интерференционное поле без образца,
5 - поле фильтра толщиной 2,16 мкм.
Эти сдвиги отвечают
следующим толщинам слюды: Δφ1-0,63
мк, Δφ1
- 2,16 мк. То есть красный фильтр соответствовал одной длине
волны, зелёный - четырём.
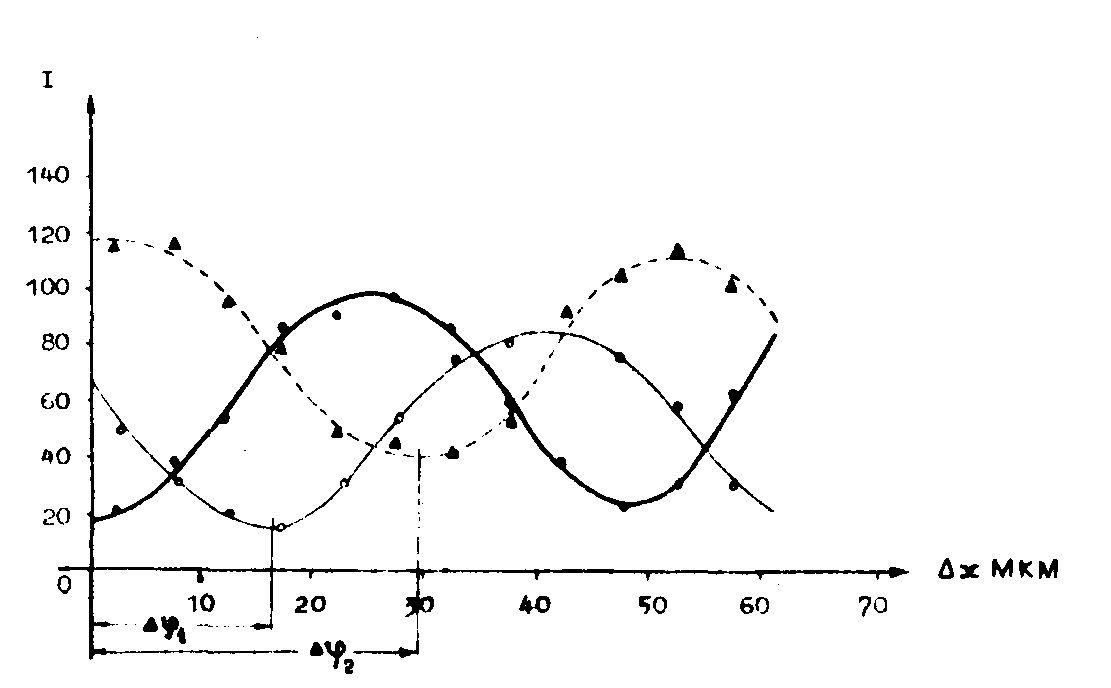
Рис.15. Изменение интенсивности интерференционных
полей при смещении дифракционной решётки.
Экспериментальная точность метода при частоте
подвижной решётки 20 лин./мм для используемых толщин образцов
порядка длины волна составляла 5°.
Отметим ряд особенностей рассмотренного метода
измерения фазового сдвига подвижной решёткой.
1. Измерение фазового
сдвига осуществляется в пределах одного периода, т.е. от 0
до 2π.
2. Подвижная решётка позволяет менять светлопольность
интерференционного изображения. Изменение светлопольности
может быть использовано при исследовании малых оптических
сдвигов.
3. При повороте подвижной решётки можно легко
переходить от бесконечной интерференционной полосы (рис.12
а,б,в) к полосам конечной ширины любой частоты (рис.12 г,д,е).
Л и т е р а т у р а
1. В.В.Добырн, Б.Г.Турухано,
Н.Турухано. Оптика и спектроскопия, 30,
550 (1971).
2. А.В.Мироненко.
Фотоэлектрические измерительное системы, изд. "Энергия",
М., 1967.
3. Г.Н.Рассудова,
Ф.М.Герасимов. Оптика и спектроскопия, 14,
406, 559 (1965).
4. Б.Г.Турухано.
Н.Турухано. ЖТФ, 38, 757 (1968).
5. Г.Н.Рассудова.
Оптика и спектроскопия, 22,
142, 473 (1967).
6. Б.Г.Турухано,
Н.Турухано. Оптика и спектроскопия, 25,
309 (1968).
7. Д.А.Асфендиаров,
В.й.Добырн, М.М.cтaбников, Б.Г.Турухано. ПТЭ, 2,
248 (1970).

