СИНТЕЗ ГОЛОГРАММ
НА ЭЛЕКТРОННЫХ ВЫЧИСЛИТЕЛЬНЫХ МАШИНАХ
Б.Е.Хайкин
Рассмотрены вопросы синтеза голограмм на электронных вычислительных машинах, включая этапы синтеза голограмм, вычисления функций, позволяющих осуществить вывод голограмм из Э В М, и вывода синтезированных голограмм. Показано, что синтез голограмм на ЭВМ позволяет решать задачи создания машинных дисплеев, синтеза фильтров для обработки информации и моделирования голографических процессов.
Проблема нашивного синтеза голограмм возникает из нескольких задач, решение которых представляется перспективным для ряда прикладных областей техники, в основном связанных с обработкой информации .
1. Возможность машинного синтеза голограмм объектов, представленных в виде математических формул. Такие объекты могут быть результатом решений на ЭВМ различных задач, а том числе конструкторско-технологических. Синтезированные голограммы должны обеспечить вывод из Э В М двух- и трёхмерных объектов.
2. Синтез машинных фильтров для распознавания образов и обработки информации, в том числе синтез комплексно-сопряжённых фильтров для объектов, меняющихся в пространстве и во времени.
3. Возможность сочетания методов оптической и машинной обработки информации, обработка голограмм на ЭВМ, машинные и оптические преобразования в изображениях и спектрах.
4. Моделирование на Э В М операций обработки инфоркации на основа машинных и обычных голограмм, моделирование решения задач,
использующих оптические принципы.
Машинный синтез голограмм состоит из нескольких этапов, имеющих свои специфические проблемы.
Первым этапом синтеза голограмм на ЭВМ является расчёт голограммы для объекта А(х,у), представленного в виде функции или таблицы. Так как в вычислительных иашинах для расчётов применяются приближенние методы, то необходимо разработать для синтеза голограмм приближенные методы, обеспечивающие требуемую точность при сравнительно небольшом времени вычислений.
Вторым этапом синтеза голограмм является вычисление функций, позволяющих осуществить вывод голограмм из ЭВМ с учётом характеристик конкретных устройств вывода, так как вывод голограмм из ЭВМ может осуществляться в виде геометрических фигур, пятен, различных размеров и плотностей.
Третий этап синтеза голограмм сосюид в выводе голограмм из ЭВМ при помощи графопостроителей, электронно-лучевых трубок, печатающих устройств.
Четвертый этап синтеза голограмм заключается в записи синтезированного изображения (голограммы) на различных материалах.
Перейдём к этапу синтеза голограмм на ЭВМ. Первоначально возникает вопрос представления изображения, для которого синтезируется голограмма. Двумерное изображение А(х,у) или трёхмерное изображение А(х,у,z) вводятся в память ЭВМ в виде набора дискретных величин, т.е.
a(x,y) = (aij)m,n,
(1)
a(x,y,z) = (aijk)m,n,p.
В частности, для двумерного случая величина aij соответствует яркости в точке с координатами (xij). Шаг дискретизации для неискажённой передачи изображения выбирается, исходя из объёма запоминающего устройства ЭВМ и требований теоремы Котельникова. Вследствие ограниченности объёма памяти и большого времени вычисления в настоящее время осуществляется ввод и синтез сравнительно простых изображений. Самая большая голограмма /1/
содержала 106 элементов, ввод изображений в Э В М может осуществляться при помощи видикона с преобразованием или посредством кодирования изображений с записью на перфокарты или перфоленту. Например, для ввода изображений с 128х128 элементов с 32-мя градациями каждый требуется 105 бит памяти, для сетчатки 1024 х 1024 - 5∙106 бит.
По методу синтеза гилограммы можно клаисифициролять на голограммы, создаваемые на основе преобразования Фурье /2/, на основе расчёта френелевских зонных пластин /3/ и на основе вычис ления комплексного вектора электромагнитного поля /4/ . Наибольшее распространение получил синтез голограмм на основе преобразования Фурье /2,5,6/, к рассмотрению которого мы и перейдём.
Известно, что в оптике пара преобразований Фурье может быть представлена в виде
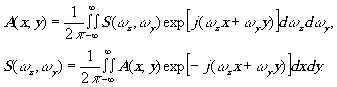(2)
Переход к дискретному представлению преобразований Фурье характеризуется заменой интеграла (2) дискретными рядами
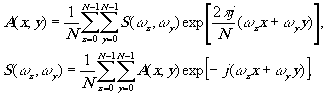(3)
которые вьписляются для n2 точек решётки m х n. Такой переход от преобразования Фурье (2) к дискретному ряду естественно приводит к приближенным вычистениям. Шаг дискретизации ∆m, ∆n выбирается на основе теоремы Котельникова. Переход от непрерывных функций к дискретным рядам возможен для функций с ограниченной пространственно-частотной характеристикой, т.о. при переходе пред-
полагается, что спектр функции ограничен. Заметим, что в реальных оптических голограммах из-за зернистости фотоэмульсии фактически записывается функция с ограниченным спектром, т.е. ограничение спектра в синтезированных голограммах имеет аналогию в оптике.
Для вычисления преобразования Фурье на ЭВМ первоначально его нужно привести к одномерному случаю. На основе тригонометрического представлечия рядов Фурье спектр функции можно представить в виде
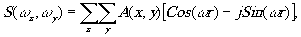(4)
где ωr = ωxx+ωyy, и в виде следующего разбиения:
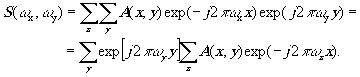(5)
Таким образом, необходимо вначале вычислить преобразование Фурье
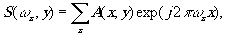(6)
соответствующее одномерному случаю. Это преобразование вычисляется для всех строк последовательно, а затем нужно перейти к вычислению одномерного преобразования по столбцам, т.е.
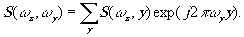(7)
Для вычисления преобразования Фурье на Э В М по формуле (7) необходимо выполнить n4 операций сложения и n4 операций умножения над комплексными числами. Отметим, что для выполнения сложения или умножения над комплексными числами нужно произвести 5÷7 машинных операций, т.е. общее число машинных операций составляет n5 операций.
Практическое распространение получил метод быстрого выполнения преобразования Фурье, так называемый метод Кули-Туки /7/.
Метод быстрого преобразования Фурье (БПФ) основан на принципе факторизации матриц, т.е. разбиении матриц на простые сомножители. Вычисление комплексного преобразования Фурье для одномерного случая можно записать как
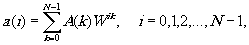(8)
где А(к)- комплексный коэффициент Фурье, а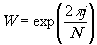 
. Величину n можно представить в виде произведения n= r1·r2, тогда индексы в (8) перепишутся в виде n= r1·r2,
i=i1r1+i0; i0 = 0,1,…,r1-1: i1 = 0,1,…,r2-1, (9)
k=k1r2+k0; k0 = 0,1,…, r2-1; k1=0,1,…,r1-1.
Вычисление преобразования Фурье соответственно изменится, т.е.
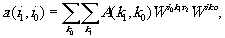(10)
но так как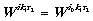 
, а внутренняя сумма в (10) по k1
зависит только от i0 и k0, то получим
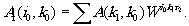(11)
Или окончательно
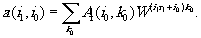(12)
Для n элементов в А1(i0,k0) нужно выполнить n r1 операций, а для вычисления а(i1, i0) из a1 требуется выполнить n r2 операций, т.е. всего r= n(r1+r2) операций. Отметим, что вычисление (8) требует n2 операций. При разбиении на сомножители получим
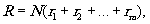(13)
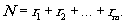(14)
Принимая r1=s1t1 при si, ti>1 т.е. si + ti < ri, а также считая, что si ≠ ti ≠ 2, получим si + ti = ri. Приравнивая ri = r,
перепишем (14) в виде
m=logrn, (15)
r=r n logrn.
Общее число операций для одномерного случая равно 2 n logn, с учётом операций над комплексными числами - 10 n lоgn машинных операций. Для двумерного случая, соответственно, получим 2n2logn и 10 n2logn, т.е. примерно на два порядка быстрее, чем при обычном вычислении преобразования Фурье.
Для практического вычисления Б П Ф составляются мнемонические схемы, которые могут быть получены на основе преобразования графов. Возьмем первую строку сетчатки m∙n, т.е.
Аo(,0), АО(1), Аo(2), ..., АО(n-1). (16)
Затеи составим линейные комбинации 1-го и n/2 членов, 2-го и (n/2+1) и т.д. Это будут коэффициенты первой группы. Затем составим линейные комбинации 1-го и n/4 - членов, 2-го и (n/4+1 ) и т.д. до половины первой группы, симметрично для второй группы. Разбиение продолжаем до тех пор, пока в группе будут комбинации соседних членов, т.е.
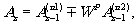(17)
где х - номер группы, а
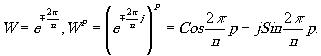(18)
Для обратного преобразования Фурье
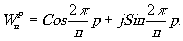(19)
При машинном преобразовании Фурье легко перейти к комплексно-сопряженный величинам, что достигается простой заменой знака перед мнимой частью, т.е. (а 7
jb) → (а ±jb).
С теоретической точки зрения задача построения голограиим сводится к нахождению функции s(ωx,ωy). Так как лобое изображение А(х,y) можно рассматривать как конечную функцию, то со-
гласно условиям Дирихле она может быть аппроксимирована рядом Фурье (для периодической функции) или интегралом Фурье (для непериодической функции), т.е. для последнего случая получим
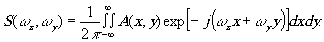(20)
Для функции А(х,у) вводим два ограничения: по размерам и по разрешающей способности, т.е.
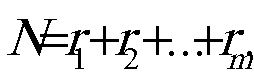(21)
Исходя из разрешающей способности a(x,y), величина голограммы, т.е. функции s(ωx,ωy), также получает ограничения
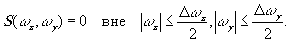(22)
Ограничение величины изображения позволяет определить разрешающую способность синтезированной голограммы δω≤1/Δx.
На основании теоремы Котел ьникова функция s(ωx,ωy) полностью определяется рядом комплексных параметров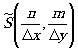 
и выборочных точек:
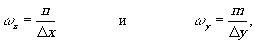
где m,n=0,1,…,n-1;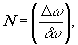 
(23)
тогда функция s(ωx,ωy) запишется в виде
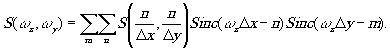(24)
Функция изображения А(х,у) в этом случае может быть представлена как преобразование Фурье от функции
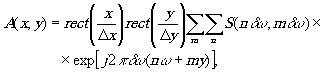(25)
где ωx=δωn и ωy=δωm. Заметим, что sinc(α) θ rect(x), соответственно, означают sinc(α)=sinπα/πα
1 |x|<1
rect(x) = (26)
0 |x|≥1
Аналогично, если известна функция А(x,y), то при помощи преобразования Фурье можно определить функцию s(ωx,ωy).
Наиболее трудоёмким процессом при создании синтезированных голограмм является процесс записи комплексного спектра на плёнку, т.е. фактически транспарант должен иметь вид голографии. Для записи комплексного спектра предварительно производится амплитудное и фазовое кодирование. Основой для фазового кодирования спектра является свойство дифракционных решёток с дефектом вызывать деформацию волнового фронта, т.е. сдвиг фазы. Для идеальной дифракционной решётки сдвиг фаз между двумя лучами (рис.1), выходящими иа соседних щелей решётки, составляет 2π в первом дифракционном порядке. Если щели смещены, то разность хода между смещённой и соседней щелью будет отлична от 2π и пропорциональна величине смещения.
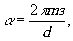
где d - период идеальной решётки, m - порядок спектра, р- величина смещения периода идеальной решётки. Таким образом, положением щели можно задать фазу комплексной функции. Амплитудное кодирование для бинарных голограмм основано на изменении ширины щели дифракционной решётки, т.е. изменении светопропускаемости дифракционной решетки.
Итак, комплексную функцию можно представить посредством построения многих параллельных щелей соответствующей вирины и соответствующего положения.
После вычисления на Э В М комплексной функции s(ωx,ωy), представленной рядом комплексных величин s(n/Δn,m/Δy) и выборочных точек, производится вычерчивание голограммы h(ωx,ωy). Голограмма должна представлять такую двоичную функцию, которая удовлетворяла бы следующему условию:
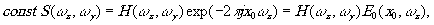(27)
где Е(х0,ωx)- наклонная плоская волна. Функция s(ωx,ωy) создаётся посредством освещения двоичной голограммы Н(ωx,ωy) плоской наклонной волной Е(х0,ωx). Построение голограммы производится следующим образом. Каждая из выборочных точек s(n/Δx, m/Δy) окружается квадратом с площадью (δω)2. Такой квадрат называется элементарной ячейкой. Считаем, что в достаточно налой ячейке функция s(nδω,mδω) пичгти постоянна, т.е.
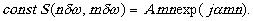(28)
На каждую ячейку в этом случае приходится один комплексный параметр, но так как голограмма может содержать только действительные параметры, то на каждую ячейку голограммы Н(ωx,ωy) приходится два действительных параметра, эквивалентных комплексному параметру.
Существует много способов приписывания двух параметров: по величиче, положению, форме пятен в ячейке. С точки зрении вычерчивания элементарных ячеек двухкоординатным графопостроителем наиболее просто взять прямоугольник с переменной высотой wδω и постоянной шириной Сδω и переменным положением Рδω (πис.2).
При использовании вместо графопостроителя электронно-лучевой трубки форма пятна круглая и величина амплитуды amn отображается изменением яркости пятна imn, величина фазы αmn задаётся положением Рmn пятна отнисительно центра ячейки (рис.3).В этом случае уравнение (27), описывающее случай прямоугольного отверстия, заменяется уравнением (29) для круглых отверстий:
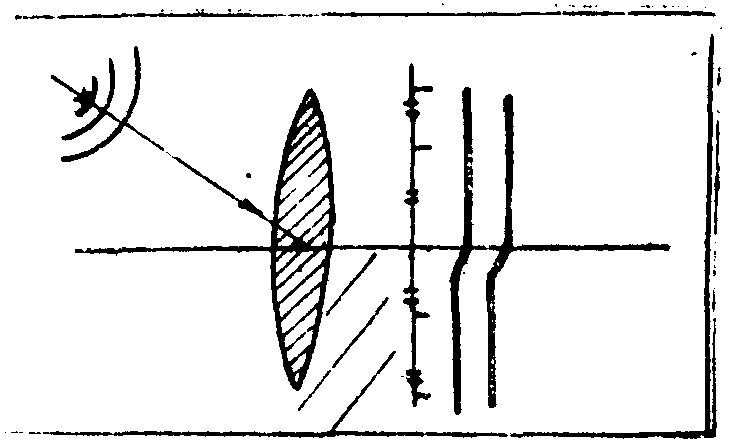
Рис.1. Сдвиг фаз на основе смещения щелей в дифракционной решетке.
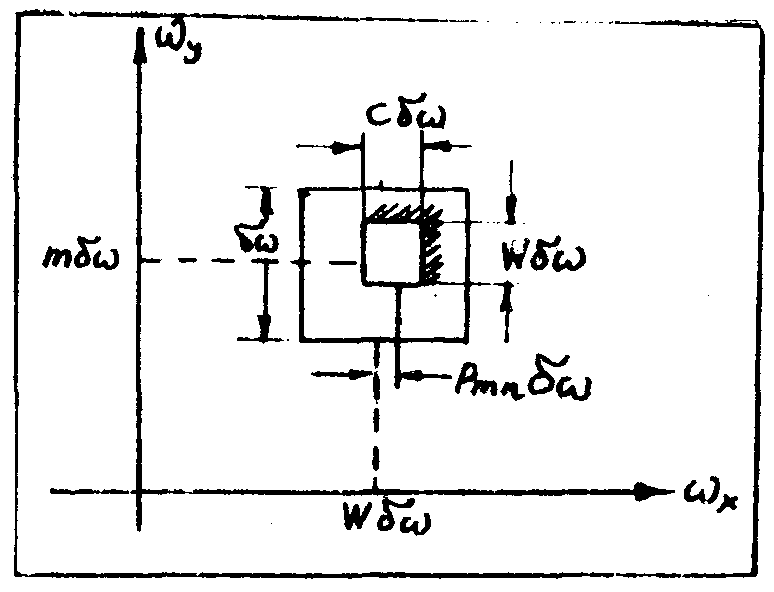
Рис.2. Элементарная ячейка синтезированной голограммы в виде прямоугольника.
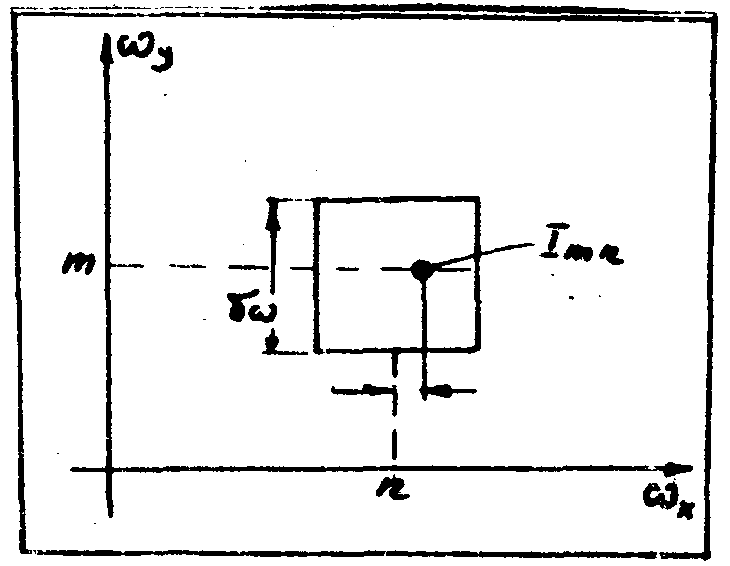
Рис.3. Элементарная ячейка синтезированной голограммы в виде круглого отверстия.
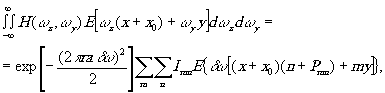(29)
где r = [(x+x0)2+y2]1/2, а aδω- πадиус распространения пятна яркости. Если внести следующие допущения
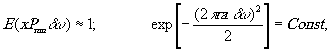(30)
то получим
imn ≈ amn, pmn ≈ φmn/2 (31)
Это даёт возможность реализовать комплексную величину изложенным способом на электронно-лучевой трубке.
В ряде случаев синтез и вывод голограмм на Э В М может быть существенно упрощён, если ввести предположение о постоянстве амплитуды пропускания элементов изображения и представлении изображения в виде точечных объектов /4/.
Дальнейшее упрощение метода может быть выполнено на основе преобразований вектора электромагнитного поля, описывающего точки синтезированной голограммы, и учёта некоторых физических условий восстановления голограммы /8/ .
Синтез голограмм может быть осуществлён на основе киноформа /6/.
Киноформ представляет собой отбеленную фазовую голограмму. От френелевской фазовой голограммы киноформ отличается отсутствием опорного пучка. Киноформ не имеет дифракционных порядков при восстановлении, что достигается посредством отбеливания и согласования фаз.
Расчёт киноформа можно выполнить на основе формулы Френеля-Кирхгофа:
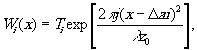(32)
где Тi = 1 или 0. Результирующий волновой фронт запишется в виде
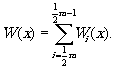(33)
Перейдём к анализу третьего этапа синтеза голограмм - выводу синтезированных голограмм из ЭВМ. При этой возникает ряд вопросов, связанных с точностью передачи амплитуд синтезированных голограмм, выбора размеров голограммы, а также учёта свойств носителя, на котором фиксируется голограмма.
Синтезированная голограмма в общем случае получается в виде комплексной функции
a(x,y)=a(x,y)exp[jφ(x,y)], (34)
где a(х, y)- распределение амплитуд, а φ (x,y) - распределение фаз. На основе (34) можно описать два типа голограмм: полную голограмму, имеющую распределение амплитуд и фаз, а также фазовую голограмму, т.е.
a(x,y)=exp[jφ(x,y)], (35)
в которой модуль амплитуды отбрасывается. Такое допущение может быть сделано в избыточных голограммах, так как в стучае диффузных волновых фронтов амплитудной информацией можно пренебречь. На этом принципе основано построение синтезированных фазовых голограмм, в частности киноформа.
Вывод синтезированных голограмм может быть осуществлён при помощи электроино-лучевых трубок. Наиболее простой случай вывода соответствует фазовым голограммам, так как при этом требуется отображать только один параметр. При выводе комплексных голограмм размеры пятна могут соответствовать амилитуде, а смещение луча относительно нулевого положения - фазе (рис.3).
Максимально допустимое расстояние между точками голограммы, которое позволяет получать разделение изображений высших порядков может быть определено как αmax = λf/s, где s- размер изображения высших порядков, f - фокусное расстояние восстанавливающей линзы.
Л и т е р а т у р а
1. l.В.lеsеm et al. communs. of the acm, 11, 11, 70, 1969.
2. a.w.lohmann. d.p.paris. josa, 56, 4, 535, 1967.
3. i.p.waters. appl.phys.lett., 9, 405, 1966.
4. s.e.keeton. proc.ieee, 56, 3, 325, 1968.
5. a.w.lohmann. appl. optics, 6, 9, 1967.
6.l.В.lesem et al. ibm res. and develop., 13, 2, 150, 1969.
7.j.w.cooley, j.w.tukey. mathem. of comput., 19, 267, 1967.
