МОДЕЛИРОВАНИЕ ГОЛОГРАФИЧЕСКИХ МЕТОДОВ ОБРАБОТКИ ИНФОРМАЦИИ НА ЭЛЕКТРОННЫХ ВЫЧИСЛИТЕЛЬНЫХ МАШИНАХ
Б.Е. Х а й к и н
Рассмотрены вопросы моделирования на Э В М операций оптической обработки информации. Описаны основные алгоритмы, реализующие моделирование, и структура оптической обработки информации с оптическими решающими фильтрами, исследованная на машинной модели.
Постановка задачи
Моделирование голографических методов обработки информации на Э В М предназначено для исследования следующих вопросов.
1. Моделирование на Э В М операций обработки информации, использующей голографические методы. Моделирование на ЭВМ позволяет при помощи количественных характеристик оценить различные типы операций, учитывая при этом случайный характер ряда физических процессов, используемых в операциях обработки информации (зернистость фотоматериала, нелинейность фотопроцесса, неоднородность луча лазера и т.п.).
2. Моделирование на ЭВМ вычислительной структуры, состоящей из когерентной оптической системы и электронной вычислительной машины. Такое объединение позволяет наиболее полно использовать достоинства когерентной оптики и Э В М. При помощи
ЭВМ в этом случае можно осуществить синтез оптических решающих фильтров (ОРФ) для обработки информации. Следует отметить, что машинный синтез ОРФ существенно расширяет возможности когерентных методов обработки информации, так как на ЭВМ можно синтезировать большую группу ОРФ, создание которых оптическим путём не представляется возможным.
3. Моделиривание на Э В М методов решения задач на основе О Р Ф и указанной выше структуры. Хотя использование когерентных методов обработки информации открывает новые возможности в создании вычислительных методов для решения различных задач, эффективность применения голографических методов для различных задач неодинакова. Моделирование методов решения позволяет оценить эффектииность голографических методов для различных типов задач и определить требования к физическим параметрам устройств когерентной обработки информации.
4. Моделирование различных схем голографии и преобразований в когерентных оптических устройствах.
Блок-схема структуры, на которой выполняется моделирование, представлена на рис.1, где КОС - когерентная оптическая система обработки информации (например, обычное устройство для оптической фильтрации), у1 - устройство ввода изображений в Э В М (видикон с преобразователем аналог-код) и у2 - устройство вывода синтезированных голограмм и ОРФ из ЭВМ (напрпыер, вывод на электронно-лучевую трубку с последующим уменьшением изображения).
Для моделирования на Э В М голографических методов обработки информации необходимо выполнить на Э В М оснорные преобразования, характерные для когерентной оптики. Основное отличие моделирования на Э В М от реальных оптических устройств состоит в дискретном характере представления информации. Преобразование Фурье, имеющее в оптической системе вид
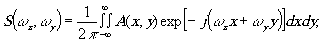 (1)
(1)
заменяется на Э В М двойным произведением
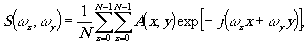
Рис.1. Блок-схема вычислительной структуры для моделирования.
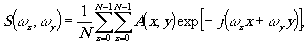 (2)
(2)
для n2 точек решётки n×n. При этом, естественно, возникают приближения, определяемые дискретным характером обработки информации .
В основе математического моделирования голографических методов обработки информации находится синтез голограмм на ЭВМ /1/ при помощи быстрого преобразования Фурье.
Модель на ЭВМ состоит из ряда алгоритмов, соответствующих различным оптическим преобразованиям. Помимо алгоритма синтеза голограмм, в модель включаются алгоритмы умножения изображения и спектров, алгоритм формирования случайных двумерных функций с заданным законом распределения вероятностей, алгоритм изменения модулей и фаз спектра. В модель также входят различные дискретные операции, выполнение которых на ЭВМ осуществляется при помощи элементарных операций. К числу таких операций относится инверсия изображений, логическое сложение, операция маскирования, операции сдвига изображений и преобразований спектров. При синтеза на ЭВМ оптических решающих фильтров появляется возможность создания фильтров, инвариантных к повороту и контрасту, для чего в модель включаются программы поворота и нормализации. Для обработки реаультатов операций в когерентной оптической системе в состав модели необходимы также включить алгоритм статистической обработки информации. При помощи такого алгоритма можно, в частности, определить порог распознавания на основе согласованной фильтрации с учётом искажений в различных устройствах.
Рассмотрим кратко некоторые из этих алгоритмов. Для выполнения перемножения двух изображений А(х,у) к В(х,у) необходимо последовательно перемножить их одноименные элементы, представленные в виде комплексных величин
c1 = a1+jb1, c2 = a2jb2
по следующему правилу:
c1c2 = (a1a2 - b1b2) + j(a1b2 + a2b1). (3)
При помощи алгоритма преобразования Фурье и перемножения можно выполнить различные интегральные преобразования.
Для формирования комплексно-сопряженных величин спектров и изображении необходимо преобразовать кошпексные значения по правилу А→А*, s→s* , т.е.
(а ± jb) →(a 7
jb).
Для формирования случайных двумерных функций, моделирующих различные виды помех, применяется алгоритм машинного формирования псевдослучайных величин. Для одномерниго распределения каждый элемент аij, можно представить в виде функции распределения
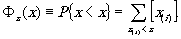 (4)
(4)
Для двумерного распределения нужно сформировать псевдослучайные значения по координатам х и у. Распределения случайных координат аij (х1,х2) можно определить при помощи вероятностей
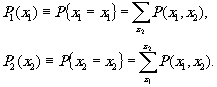 (5)
(5)
Следует отметить программ, для изменения модулей и фаз в изображениях и спектрах. Изменение амплитуд и фаз производится по правилу
[а(х,у) ± b(х,y)] и [ φ(x,y) ± Ψ(х,y)]. (6)
На основе этой програмыы можно осуществить коррекцию частотно-контрастной характеристики.
На основе моделировании на ЭВМ можно рассмотреть вычислительную структуру, приведённую на рис.1. В основе этой структуры находится применение оптических решающих фильтров для обработки информации.
Рассмотрим оптическое когерентное устройство, состоящее из лазера и набора плоскостей Р1, Р2,..., Рn, в которых рассматривается преобразование информации, поступившей на вход Р1. Для простоты рассмотрим устройство, состоящее иа трех плоскостей, лазера и набора фильтров, размещаемых в любой из этих плоскостей (рис.2).
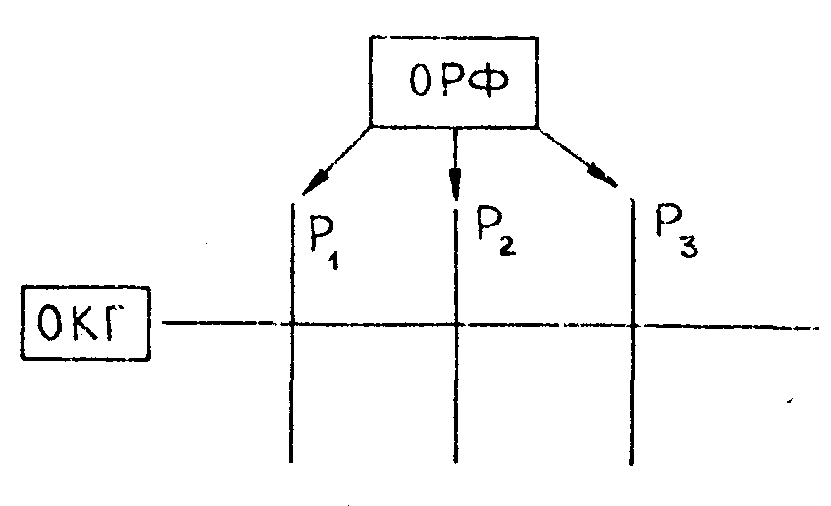
Рис.2. Схема когерентной оптической системы обработки информации.
Входная информация представлена в виде транспаранта с двумерной функцией А(х,у), т.е. оптического изображения. В частном случае А(х,у) представляется в виде матрицы из конечного числа элементов aij, т.е. А(х,у) = (аij)m,n , где aij представляется в виде двоичного кода (aij = 1,0 ), либо многоградационного кода (aij = 0,1,2...,р).
Предположим, что необходимо преобразовать функцию А(х,у) в функцию А(х,у) или аналогично преобразовать таблицу А(х,у), т.е.
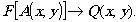 (7)
(7)
В общем случае преобразование q(x,y) получается в результате последовательного набора преобразований f1, f2,..., fr , т.е.
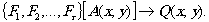 (8)
(8)
Требуется доказать, что на основе свойств оптического когерентного канала и посредством размещения различных fi в плоскостях Рi можно обеспечить преобразование А(х,у) в q(х,у)для достаточно большого класса операций передачи и обработки информации, т.е. создать достаточно универсальное вычислительное устройство на основе ОРФ. Заметим, что в виде (8) можно представить любой вычислительный алгоритм, но если в ЭВМ преобразования представляют собой элементарные операции (сложение, сдвиг и т.п), то в оптике возможно выполнение за один такт сложных преобразований, эквивалентных сложным алгоритмам на Э В М.
Оптические характеристики устройства описываются ел едущими тремя свойствами.
Свойство 1. При освещении плоской волной когерентного света плоскости Рi, в которой размещён транспарант А(х,у) на выходе, получим распределения фаз φ(х,у) и амплитуд а(х,у), т.е.
А(х,у)=а(х,у)ехр[i φ(υ,у)]. (9)
Свойство 2. Между любой парой плоскостей выполняется оптическое преобразование Фурье. Если информацию в плоскости Рi представить в виде двумерной функции А(х,у), то в плоскости Рi+1 получим функцию спектра
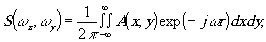 (10)
(10)
где ωr = ωxx+ωyy, a ωx и ωy - круговые пространственные частоты. В плоскости Рi+2 получим обратное преобразование Фурье:
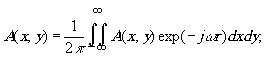 (10)
(10)
Физически преобразование Фурье выполняется при помощи двояковыпуклой линзы, размещаемой меэвду плоскостями Рi и Рi+1.
Свойство 3. При нахождении в плоскости двух транспарантов и освещении когерентным светом их амплитуды пропускания перемножаются, т.е.
С(х,y)=a(х,y)В(х,y)=а(х,y)b(х,y)ехр{j[φ(х,y)+Ψ(x,у)]}. (12)
Исходя из перечисленных свойств, можно построить большую группу преобразований, часть из которых приведена в таблице 1.
Таблица 1
|
pi |
pi+1 |
|
s1*·s2
a1·a2
s1Ä
s2
a1**
a2
a1Ä
a2 |
a1**
a2
s1Ä
s2
a1·a2
s1*·s2
s1·s2 |
Здесь индекс * означает комплексно-сопряжённые величины, символ Ä
- свёртку, а символ *
- корреляцию между двумя функциями.
На основе рассмотренных свойств когерентного оптического канала и всевозможных преобразований можно свести задачу обработки информации к формированию оптических фильтров, размещаемых в плоскостях Р1,Р2,…,Рn.
Одной из наиболее существенных операций, выполняемых на основе ОРФ является распознавание образов при помощи комплексно-сопряжённых фильтров. Пусть А(х,у) описывает страницу текста, в которой.необходимо найти искомый образ (букву или слово). Обозначим искомый образ через С(х,у) и представим А(х,у) в виде сочетания полезного сигнала и помехи n(х,у), т.е.
А(х,у)=С(х,у)+n(х,у). (13)
Операция выделения искомого образа выполняется на основе фильтра, представяяющего комплексно-сопряжённый спектр искомого объекта, т.е.
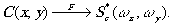
Если такой фильтр расположить в плоскости Р2, то в плоскости Р3 возникает яркая точка в месте нахождения образа в плоскости (рис.1).
Оказанную операцию символически можно представить в виде
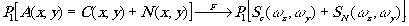 (14)
(14)
Размещая фильтр 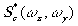 в плоскости Р2, получим
в плоскости Р2, получим
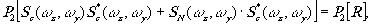 (15)
(15)
тогда
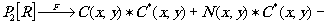 (16)
(16)
максимум корреляции в (16) соответствует распознаваемому образу. Существенными достоинствами комплексно-сопряжённого фильтра является обеспечение им максимального отношения полезного сигнала к помехе, а также инвариантность фильтра к параллельному сдвигу образа.
Следующая операция, относящаяся к передаче информации, связана с сокращением избыточности на основе неравномерного распределения информативных признаков в спектре изображения. Не останавливаясь на методах выбора информативных частот, можно утверждать, что все они выражаются в виде некоторой маски М(х, у ), вырезающей частоты из спектра s(ωx, ωy). В частности были предложены методы выбора информативных частот на основе гипотезы о расположении информативных частот вблизи координатных осей /2/ или на основе выбора информативных частот на основе метода Монте-Карло /3/.
При представлении А(х,у) в виде дискретного матричного кода (aij)mn над ним можно выполнить полный набор элементарных логических операций. Логическое сложение двух матричных кодов А(х,у) ⋁ В(х,у) для всех аij ⋁ bij выполняется при наложении двух изображений А(х,у) и В(х,у) в плоскости Рi при условии, что аij = 1 соответствует прозрачность, равная нулю.
Сложение двух изображений выполняется на основе отношения (s1+s2)→ (А1+А2), т.е. сумме спектров соответствует сумма изображений. Вычитание изображений может быть получено посредством примененbя ОРФ в виде фазовой π -пластинки. Тогда
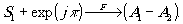 (17)
(17)
Операция инверсии дискретного матричного кода выполняется на основе операции вычитания, т.е.
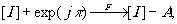 (18)
(18)
где [i] соответствует некоторая постоянная.
Наличие операций логического сложения и инверсии позволяет выполнить логическое умножение, так как 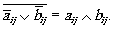
Рассмотрим группу операций, отноонщуюся к преобразованиям над отдельными элементами матричного кода: строками rakj = ak1,ak2,...,аkn, столбцами sаik = а1k,...,ank и зонами zaij т.е. отдельными участками А(х, у). Кодирование строк, столбцов и зон мо;но выполнить на основе двоичных кодов или в виде аналоговых величин, при которых ка;дому коду соответствует либо различная оптическая плотность элементов аij, либо количество элементов аij = 1. С помощью операции логического умножения осуществляется маскирование, т.e. выделение требуемых rakj, sаik и zaij из А(x,у). На основе операции маскирования и оптимальной фильтрации можно создать ОРФ для нахождения минимальных и максимальных значений строк, столбцов и зон.
Таким образом, на основе описанных выше различных типов фильтров и операций появляется возможность создания достаточно универсальных вычислительных устройств.
Одним из вопросов, возникающих при практической реализации КСФ, является выбор метода определения некоторого порога, позволяющего с требуемой степенью достоверности производить распознавание объектов с учётом ряда специфичных особенностей и недостатков КСФ /4, 5/. Хотя отношение сигнала к помехе на выходе КСФ достигает в отдельных случаях 150:1, 200:1, но за счет недостатков это отношение уменьшается. Кроме того, наличие поро-
га позволяет осуществлять одновременное распознавание большого числа однородных объектов, а также распознавание по фрагменту.
После обработки некоторой реализации f(t)=х1, x2, ...,xn, представляющей видеосигнал на выходе сканирующего устройства системы распознавания, получается одна или несколько точек, соответствующих максимальной яркости. Рассмотрим несколько реализации (У/o), содержащих только различные помехи, и несколько реализации (У/s), содержащих сигнал и помеху одновременно. Из каждой реализации используем одно максимальное значение яркости, считая, что в одной реализации (У/s) может быть один объект. Затем для реализации (У/О) и (У/s) определяем закон распределения случайных величин. В большинстве практических случаев можно принять, что сигиал и помеха распределены по нормальному закону. Оценки параметров определяем иднии из известных методов /6/.
Плотность вероятности Р0(х), соответствующая распределению максимальных яркостей в реализациях типа (У/О), будет
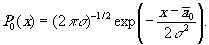 (19)
(19)
Соответственно для реализации (У/s) запишем
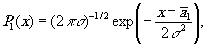 (20)
(20)
где 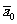 , и
, и 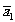 - средние значения, а σ2 - дисперсия. Затем в зависимости от априорной информации и типа решаемой задачи применяем критерий Байеса, минимаксный или Неймана-Пирсона. Для всех этих критериев необходимо вычислить коэффициент правдоподобия ⋀(x)=Р1(x)/p0(x), который сравнивается с пороговой величиной ⋀0. Если ⋀(x)< ⋀0, то верна гипотеза Н0, соответствующая наличию в реализации только помех, если ⋀(х)>⋀0, то верна гипотеза Н1, соответствующая наличию в реализации объекта.
- средние значения, а σ2 - дисперсия. Затем в зависимости от априорной информации и типа решаемой задачи применяем критерий Байеса, минимаксный или Неймана-Пирсона. Для всех этих критериев необходимо вычислить коэффициент правдоподобия ⋀(x)=Р1(x)/p0(x), который сравнивается с пороговой величиной ⋀0. Если ⋀(x)< ⋀0, то верна гипотеза Н0, соответствующая наличию в реализации только помех, если ⋀(х)>⋀0, то верна гипотеза Н1, соответствующая наличию в реализации объекта.
Для одномерного случая, соответствующего рассматриваемой системе, коэффициент правдоподобия ⋀(х) является экспоненциальной функцией от х:
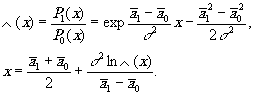 (21)
(21)
Так как экспоненциальная функция является монотонной, то решение принимается ка основе величины х, т.е. при х<х0, верна гипотеза Н0, а при х>х0 верна гипотеза х1. Выбор х0 определяется типом используемого критерия. Величина х0 определяет ошибки системы обнаружения, т.е. вероятность ложной тревоги Рлт. и вероятность Рпр пропуска объекта, которые, соответственно, равны
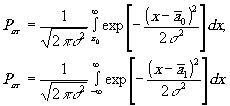 (22)
(22)
и могут быть вычислены с помощью функции Лапласа:
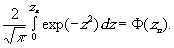 (23)
(23)
В результате вычислений получим
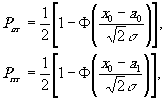 (24)
(24)
Используемые для определения порога оценки 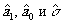 должны быть функциями от параметров, определяемых свойствами КСФ, т.е. нелинейностью фотопроцесса, неполной информацией об объекте, частичной когерентностью ОКГ, искажениями оптических систем и т.д. Одним из известных методов получения оценок определяем вышеупомянутые параметры, затем аналогично одномерному случаю определяем функцию плотности совместного распределения вероятностей для выбора порога. Для полученных оценок при помощи доверительного интервала вводятся границы для указания точности оценок.
должны быть функциями от параметров, определяемых свойствами КСФ, т.е. нелинейностью фотопроцесса, неполной информацией об объекте, частичной когерентностью ОКГ, искажениями оптических систем и т.д. Одним из известных методов получения оценок определяем вышеупомянутые параметры, затем аналогично одномерному случаю определяем функцию плотности совместного распределения вероятностей для выбора порога. Для полученных оценок при помощи доверительного интервала вводятся границы для указания точности оценок.
Л и т е р а т у р а
1. Б.Е.Хайкин. Синтез голограмм на электронных вычислительных машинах. Материалы 3 Всесоюзной школы по голографии, Л.,стр.168,1972гг.
2. Н.С.andrews, w.К.pratt. j.sос.Мot.pict.and telev.eng., 77, 12, 1279, 1968.
3. Н.i.calfiled. pieee, 57, 10, 2083, 1969.
4. Б.Е.Хайкин, В.С.Хитрова. К вопросу синтеза оптических решающих фильтров для обработки информации. Учёные записки Ереванского госуниверситета, вып.2, стр.26, 1971.
5. В.С.Хитрова, Б.Е.Хайкин. Вопросы статистической оценки оптических комплексно-сопряжённых фильтров, применяемых в задачах обнаружения. Учёные записки Ереванского госуниверситета, вып. 3, 22, 1970.
6. К.Хелстром. Статистическая теория обнаружения сигналов. И Л. 1963.

