И.Н.КОМПАНЕЦ, А.Е.КРАСНОВ, А.Н.МАЛОВ
НЕАДИАБАТИЧЕСКОЕ ВОЗМУЩЕНИЕ БИОМОЛЕКУЛЯРНЫХ ПРОЦЕССОВ ПРИ
ВОЗДЕЙСТВИИ ЛАЗЕРНОГО ИЗЛУЧЕНИЯ
Введение
Основным современнным парадоксом при применении низкоинтенсивного когерентного излучения в биологаи и медицине является все расширяющаяся сфера успешного использования лазеров при большой неопределенности механизма взаимодействия излучения с биологическими и биоподобными объектами [1]. Достаточно регулярно, например, высказываются соображения о несущественности для биостимуляции таких параметров, как степень когерентности лазерного излучения [2], но вытеснения из медицинской практики хотя бы полупроводниковых лазеров излучающими светодиодами пока не наблюдается. Нет также и убедительных результатов по сравнительному анализу биостимулирующего эффекта от когерентного и некогерентного излучения.
Действие когерентного электромагнитного излучения видимого и инфракрасного спектрального диапазона вызывает, по-видимому, однотипные структурно-оптические изменения в различных объектах [1,3,4] - биологических жидкостях, суспензиях клеток, модельных биомолекулярных растворах, клетках растений, насекомых и животных. Медико-биологические последствия лазерного воздействия крайне разнообразны, что определяется степенью биологической сложности объекта и изощренностью исследовательских методик и анализов. Энергетическая доза излучения, воздействующего на биообъект, как правило, крайне мала, и поэтому, подобно случаю КВЧ-излучения [5], следует признать такое действие "информационным", т.е. только инициирующим реакции биосистемы, протекающие за счет собственной энергии последней. В связи с относительной медленностью формирования отклика биосистемы на действие лазерного излучения, нелокальностью этой реакции при локальном воздействии (например, при лазерной акупунктуре) и большим разнообразием биохимических реакций в ответ на лазерное воздействие можно предположить наличие единого для различных биосистем физического механизма, реализующего "информационное" воздействие лазерного излучения.
В настоящей работе предпринята попытка определения на основе представлений современной квантовой радиофизики причина эффективности стимуляции биологических систем лазерным излучением.
Общие свойства биомолекулярных процессов
Наиболее общим свойством живых систем является их неравновесность и незамкнутостъ по отношению к внешней среде, что обуславливает их негэнтропийностъ, феноменологически описывающуюся в рамках неравновесной термодинамики [6]. Формально-теоретическое сходство живых организмов с также открытой квантоворадиофизической системой - лазером - отмечалось в [7]. Основой живых организмов являются биологически функциональные вещества - биополимеры, белки и нуклеиновые кислоты, обладающие большой конформационной гибкостью. Это обеспечивает наличие широкого спектра конформационных состояний макромолекул и переходов между ними при довольно низких энергетических затратах [1,6,8,11,12].
Конформационные состояния макромолекул также могут отличаться и структурой своего водного окружения. В физическом смысле такие системы имеют жидкокристаллическую структуру, характеризующуюся широким спектром метастабильных состояний, различающихся между собой конформациями биомакромолекул и связанных с ними гидратными оболочками. Поэтому действие лазерного излучения на биосистему связывается с фотоинициацией микроструктурных перестроек в таких жидких биосредах [1,8], механизм которых описывается как электронно-конформационное взаимодействие [6]. В этом случае механизм воздействия лазерного излучения можно трактовать как состоящий из первичной фотохимической реакции с переносом электрона [9] в макромолекуле с последующим конформационным изменением ассоциата, состоящего из макромолекулы и ее гидратного окружения. Другим названием комплекса таких явлений и их последствий можно считать синдром структурной альтерации биологических жидкостей, под которым понимается "трансформация структуры тканей и жидких сред организма, устойчивые структурные изменения биожидкости, проявляющиеся как локально, в области воздействия лазерного излучения, так и в биожидкостях, не подвергающихся прямому облучению" [10].
В дальнейшем под конфермером будем понимать определенное
конформационное состояние ассоциата, состоящего из одной или нескольких биомакромолекул в сочетании с взаимосвязанными с ними молекулами воды. Отметим, что определение такого ассоциата, сохраняющего на микроуровне свойства целостного организма и являющегося в этом смысле "истинной молекулой" или '"квазичастицей" всей биологической системы, является нетривиальной физической проблемой. Свойства и параметры такого ассоциата определяются, в частности, и окружением биосистемы (граничными условиями рассматриваемой задачи), что подтверждается и различием результатов экспериментов, проводимых в условиях in vivo и in vitro.
Адиабатическое возмущение биомолекулярных процессов
Рассмотрим некоторую систему NΣ биологических ассоциатов
макромолекул, находящуюся в термостате с температурой Т, определяемом окружающей средой ("организмом" см. ниже). Предположим, что выделенной системе ассоциатов отвечает G их различных конформеров (стериоизомеров) [11,12]. Для каждого конфор-мационного состояния характерен свой дискретный спектр {Ф g k}
невозмущенных электронных энергетических состояний, который при комнатной температуре (Т = 300 К° ) оказывается не заполненным (рис.1). Первые узкополосные энергетические уровни Ф g 1
конформеров (g = 1,2, ... G) соответствуют возбуждению "обобществленных" электронов (например, π-электронов), циркулирующих по макромолекулам, и практически равномерно распределены в диапазоне возбуждения ΔФG (с эквивалентным диапазоном длин волн Δλ @
100-2000 нм), включающем оптический (400 -700 нм) и ближний инфракрасный (700 - 1500 нм) диапазоны длин волн. Ширина уровней электронных возбуждений δФ g соответствует энергетической ширине ΔV g полосы колебательно-вращательных возбуждений и определяется температурой термостата δФ g @
ΔV g @
kT ( где k -постоянная Больцмана). Равновесное распределение числа N g 0 конформеров (Σ g N g 0 =NΣ ) определяется их колебательно-вращательными энергиями {V g} и равновес-
ными вероятностями W g r0 конформационных переходов, определяемыми типами ассоциатов макромолекул и внешними условиями. В равновесном состоянии должно выполняться условие баланса
ΣrN g 0W g r0 = Σ g Nr0Wr g 0 излучательных конформационных переходов.
Равновесная плотность n g 0 = N g 0 / Σ g N g 0 распределения кон-
формеров является важной характеристикой рассматриваемой биологической системы, определяющей ее способность к различным биохимическим реакциям. Другими важнейшими характеристиками данной системы являются абсолютные значения спонтанных электрических дипольных моментов d g 0 макромолекул для каждого
конформера (g = 1,2, ... G). Хотя векторы спонтанных электрических дипольных моментов индивидуальных макромолекул (или же их компонентов) расположены хаотически так, что средняя поляризация системы равна нулю, величины отличных от нуля спонтанных дипольных моментов d g 0 определяют энергии (-d g 0 Еq , q = 1,2,
... Q, где Q - количество типов клеток) их взаимодействий с электрическими полями Eq клеточных К+ - Na- насосов" и, следовательно, мембранную активность клеток, являющихся "организмом" рассматриваемой системы и задающих ее внешние условия термо-статирования. Такие условия, задаваемые при синтезе молекул клетками, влияют на количество G типов конформеров ассоциатов молекул, их строение и параметры.
При конформационных переходах наиболее простой путь удовлетворения рассмотренного выше условия баланса безизлучательных переходов заключается в детальном равновесии, при котором N g 0 W g r0 = Nr0 Wr g 0 (r,g = 1,2, ... G). Переход из состояния "g" в состояние "r" осуществляется через некоторое неравновесное конформационное состояние (отличающееся от исходного на величину Δ F g r≠- свободной энергии) с вероятностью W g r0 @
exp(-ΔF g ≠ /kT) [12]. Вероятность обратного перехода (из "r" в "g") Wr g 0 @
exp(-ΔF≠ /kT). В общем случае ΔF g r≠≠ Fr g ≠ , следовательно, N g 0 /Nr0 = Wr g 0 /W g r0 =
=exp{- (ΔFr g ≠-ΔF g ≠)/kT}.
Адиабатическое (равновесное) возмущение рассмотрении;
выше основных характеристик системы ассоциатов макромолекул а следовательно, и связанных с ними биомолекулярных процессом возможно произвести двумя путями. Первый путь связан с повы-шением температуры термостата в пределах, ограниченных тем-пературой диссоциации молекул. Свободная энергия F молекуз определяется через их среднюю электронно-колебательно вращательную энергию <U> = <Ф> + <V> и энтропию ℑ как:
F = <U> - Тℑ. При росте температуры <Ф> практически не изме-няется (т.к. kT << Ф g 1 для любого g), a <U g > = <V g > = kT. В
результате N g 0 /Nr0 = Wr g 0/W g r0 = exp{-(Δℑ≠r g - Δℑ≠ g r)/k} = const и
относительная плотность состояний конформеров не зависит от температуры термостата, т.к. полностью определяется числом из структурных многообразии. В то же время колебательной энергии молекул явно не хватает для изменения их электрических дипольных моментов.
Второй путь связан с одновременным возбуждением электронных состояний {Ф g} всех конформеров (g = 1,2, ... G) в полосе ΔФG . Это достигается использованием обычных нелазерных широкополосных источников света. Однако при этом за счет механизма безизлучательной релаксации возбуждения электронных состояний в возбуждения колебательно-вращательных состояний происходит увеличение температуры термостата, что приводит к рассмотренной выше ситуации. В то же время за счет возмущения электронных состояний должны изменяться и электрические дипольные моменты молекул.
Таким образом, адиабатические возмущения молекул системы как при ее нагреве, так и облучении широкополосными источниками естественного света не изменяют плотность распределения молекул по конформационным состояниям, а следовательно, оставляют неизменными и биохимические свойства системы в целом. С другой стороны, под действием света могут происходить изменений спонтанных дипольных моментов молекул, что может привести к изменению внешних условий системы, порождаемых активностью клеток, отвечающих за синтез данных молекул. Все это требует более детального рассмотрения процессов взаимодействия макромолекул с лазерным излучением. В частности, необходимо рассмотреть, как изменяются средние значения физических величин,
количественно описывающих рассмотренные характеристики молекулярной системы.
Неравновесная динамика молекулярных физических величин
Временная зависимость среднего значения L(t) любой физической величины, описываемой оператором 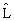 и связанной с электронными состояниями молекул рассматриваемой системы, находящихся в "g" -ом конформационном состоянии (g = l, 2, . . G), задается уравнениями [13,14]:
и связанной с электронными состояниями молекул рассматриваемой системы, находящихся в "g" -ом конформационном состоянии (g = l, 2, . . G), задается уравнениями [13,14]:
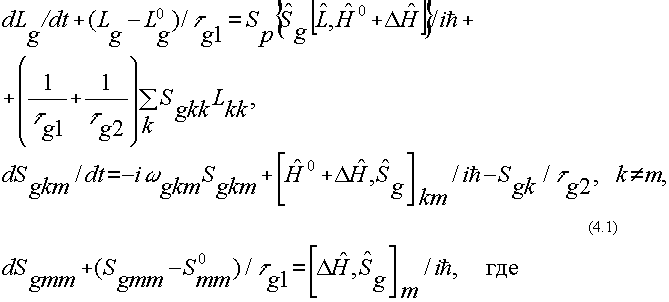
Lkm - матричные элементы оператора  физической величины L;
физической величины L;
Sgk - матричные элементы статистического оператора  плот-
плот-
ности электронных состояний "g" -ых конформеров;
Sp - обозначение суммы диагональных элементов, Sp{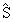 } =
} = 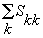 ;
;
Lg0 - среднее значение физической величины в равновесном состоянии в отсутствии возмущения, Lg0 = 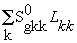 ;
;
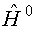 - гамильтониан системы молекул в невозмущенном cостоянии,
- гамильтониан системы молекул в невозмущенном cостоянии,
имеющий диагональную матричную форму Фgkm δkm, (где δkk = 1,
δkm=0,если k≠m);
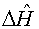 - оператор энергии взаимодействия между молекулой и лазерным светом;
- оператор энергии взаимодействия между молекулой и лазерным светом;
[] - обозначение коммутатора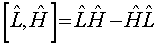 ;
;
ωgkm - частоты переходов между стационарными энергетическими уровнями электронного возбуждения молекул,
ωgkm = (Фgmm-Фgkk)/ћ;
τg1 - время спин-решеточной (продольной) релаксации электронных
возмущений g-конформеров;
τg2 - время спин-спиновой релаксации электронных возмущений g-конформеров;
ћ - универсальная постоянная (квант действия) Планка.
Как известно, в равновесном состоянии статистический оператор плотности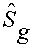 , молекулярной системы описывается диагональными элементами
, молекулярной системы описывается диагональными элементами 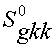 , распределенными по закону Больцмана
, распределенными по закону Больцмана
S0gkk = ехр(-Фgkk/kT). В дальнейшем будем считать, что τg1 >> τg2 для любого g-конформера.
Будем рассматривать гамильтониан возмущения молекул системы лазерным светом в приближении дипольного взаимодействия 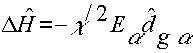 , где Eα (α=x,y) κомпоненты вектора электрической напряженности поля в воздухе, a dg α оператор
, где Eα (α=x,y) κомпоненты вектора электрической напряженности поля в воздухе, a dg α оператор
электрического дипольного момента всех переходов молекул g-кон-
формера в возбужденные электронные состояния, описываемый эрмитовой матрицей dq m α (dg m α = d*q n α). Поправочный коэффициент Лоренца χ= [(ε/ ε0 )+2]/3 учитывает действие на молекулы локального поля в условиях окружения с диэлектрической проницаемостью е. Например, если молекулы находятся в водной среде (ε = 81), то локальное поле значительно отличается от внешнего поля излучения лазера.
В дальнейшем нас будет интересовать динамика средних значений физических величин, соответствующих дипольному моменту молекул и вероятностям заполнения уровней их электронного возбуждения. В соответствии с этим из (4.1) получим:
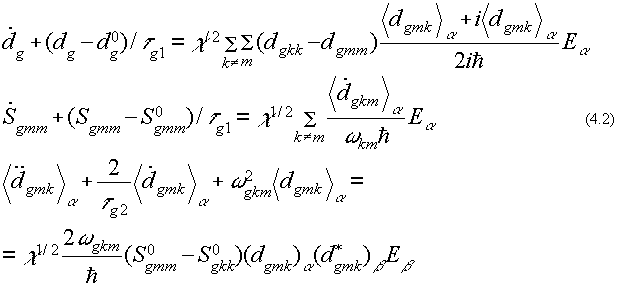
Первое уравнение в (4.2) описывает неравновесное изменение спонтанного электрического дипольного момента молекул g-конформера за счет изменения вероятностей заселенности уровней электронных возбуждений. Заметим, что данное изменение возможно лишь при условии различия диагональных матричных элементов оператора электрического дипольного момента молекул.
Второе уравнение (4.2) описывает неравновесное изменение вероятностей заселенности уровней электронных возбуждений. Третье уравнение (4.2) описывает колебательный процесс поляризации электронных переходов молекул, индуцированных полем и успевающих отслеживать его высокочастотные колебания. Последние два уравнения широко известны в оптике и лазерной физике и
используются для описания резонансных процессов поглощения и генерации света [13].
При решении последнего уравнения из (4.2) обычно принимают, что Еα = [E0α ехр (1 ω t) + Е0*a exp (-i ω t )] /2, где Е0α -
стационарная амплитуда лазерного света, а ω - его частота. Тогда в предположении близости частоты поля частотам возбуждения электронных уровней ω@
ωgkm (условие резонанса) получим:
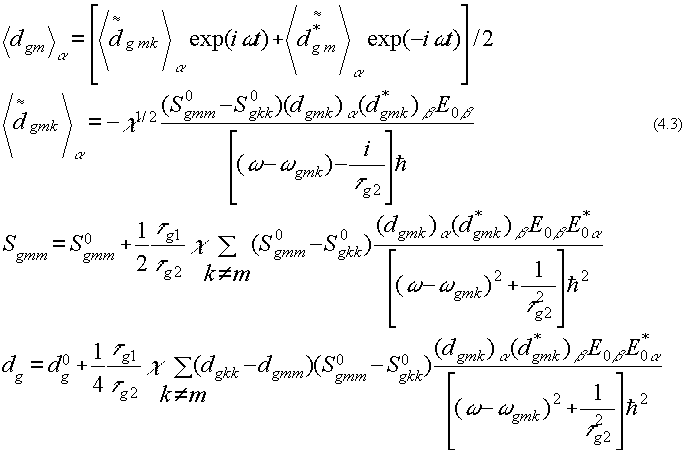
Однако упомянутое выше условие резонансного возбуждения для каждого из g-конформеров будет выполняться лишь для одного
первого электронного уровня. Учитывая также, что S0g00>>S0g11
получим:
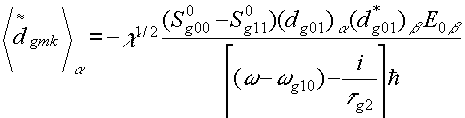
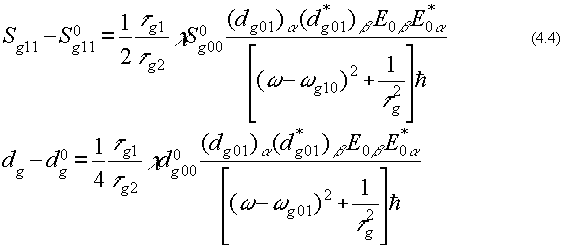
Из (4.4) следует, что возбуждения первых электронных уровней и возмущения спонтанных дипольных моментов в каждом из g-конформеров (g = 1, 2, ... G) связаны с тензором (dg01)α (d*g01)β
электрического дипольного момента перехода 0 ⇒ 1. Исходя из (4.4), можно выразить относительные изменения рассмотренных
физических величин через величину мощности P=(εε0)/2cE*0E0
лазерного света, переносимую через единицу площади, и абсолютную величину dg 01 Дипольного момента молекул:
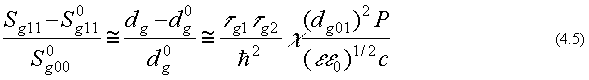
Например, для излучения Не - Ne лазера с мощностью 1 мвт/см и при водном окружении молекул с τg2@
10-6 сек,
t
g1=10-5 сек, dg01 =2 дебай, получим относительные изменения
молекулярных физических величин около 50%.
Заключение
Таким образом, в результате рассмотрения процесса взаимодействия лазерного излучения с ансамблем биомолекул показано,
что этот процесс имеет неадиабатический характер, обусловленный низкополосным (монохроматическим) характером спектра излучения. Второстепенное значение при этом имеет абсолютное значение длины волны лазерного излучения. Воздействие на биомолекулярную систему излучения обычных источников света аналогично адиабатическому повышению температуры всей системы в целом, а действие монохроматического, узкополосного лазерного излучения можно до определенной степени уподобить механическому перемешиванию биожидкости.
Описание эффекта лазерной биостимуляции в терминах теоретической квантовой радиофизики представляет, по нашему мнению, существенный интерес и открывает значительные перспективы в интерпретации имеющегося экспериментального материала по лазерной биомедицине. Так, в частности, можно предположить, что плодотворным окажется применение результатов, полученных в синергетике, теории странных аттракторов и динамического хаоса [15]. Основной задачей при этом окажется адекватная биологии и медицине интерпретация соответствующих радиофизических и квантовомеханических понятий.
Строго говоря, проведенное рассмотрение соответствует режиму импульсного лазерного облучения биосистем. Распространение анализа на случай непрерывного облучения требует учета явлений пространственно-анизотропной диффузии конформеров, что может быть описано в рамках фрактальной концепции [16]. Также при этом необходим учет пространственной неоднородности распределения интенсивности света, которое обусловлено клеточной структурой биовещества и пространственной когерентностью лазерного излучения.
Авторы выражают благодарность за плодотворные обсуждения А.А.Васильеву, Е.Я.Гаткину, И.Б.Лапрун, С.Н.Малову, Л.Д.Писларюку, Е.П.Пожедаеву, И.П.Ревокатовой и В.В.Черному.
Литература
1.Илларионов В.Е- Основы лазерной терапии. М.: РЕСПЕКТ, 1992. 124с.
2.Палеев Н.Р., Карандашов В.И., Коган Л.М., Зродников B.C., Петухов Е.Б. Использование высокоэффективных полупроводниковых излучающих диодов в фототерапевтической аппаратуре // Lazer Market, 1995. № 2-3. С.38-39.
3. Скопиков С.А., Вольф Е.Б., Курочкин С.А. Возбуждение оптико-
структурной неустойчивости в биологической жидкости низкоин-тенсивным лазерным импульсом// Письма в ЖТФ. 1991. Т. 17. Вып. 21. С.66-70.
4. Чернова Г.В., Эндебера О.П., Каплан М.А. Влияние низкоинтенсивного лазерного излучения ИК-области спектра на некоторые
признаки дрозофилы// Физическая медицина. 1992. Т.2. № 1-2. С 35-
39.
5. Девятков Н.Д., Голант М.Б, Бецкий О.В. Миллиметровые волны и их роль в прцессах жизнедеятельности. М.: Радио и связь,
6. Волькенштейн М.В. Общая биофизика. М.: Наука, 1978 592с
7. Cin Qiao. Analogy between life phenomenon and laser// Chin J Infrared Res. A. 1989. V.8. N 1. P. 69-74.
8. Захаров С.Д., Минц Р.И, Скопиков С.А., Чудновский В.И. Действие электромагнитного излучения на биологические объекты и лазерная медицина. Владивосток: ДВО АН СССР, 1989 С 41-52.
9. Крюков А.И., Шерсток В.П., Дилунг И.И. Фотоперенос электрона и его прикладные аспекты. Киев: Наукова думка 1982 240 с
10. Лисиенко В.И. Структурная альтерация биологических жидкостей - основа клинического применения лазера в практике лечения хирургических больных // Laser Market. 1995. № 2-3 С 9-12
11. Илиел Э, Аллинджер Н., Энжиал С., Моррисон Г. Конформа-ционный анализ. М.: Мир, 1969. 592 с.
12. Дашевский В.Г. Конформационный анализ органических молекул. М.: Химия, 1982. 272 с.
13. Пантел Р., Путхоф Г. Основы квантовой электроники. М.:
Мир, 1972.
14. Боголюбов Н.Н., Боголюбов Н.Н. Введение в квантовую статистическую механику. М.: Наука 1984
15. Shlesinger M.F., Zaslavsky G.M., Klafter J. Strange kinetics //
Nature. 1993. v363.p.31-37.
16. Федер Е. Фракталы. М.: Мир, 1991. 254 с.

