|
|
 |
 |

|
| |
Ю.Н.ВЫГОВСКИЙ, А.Н.МАЛОВ, С.Н.МАЛОВ,
П.А.ДРАБОТУРИН
СЕНСИТОМЕТРИЯ ФАЗОВЫХ ГОЛОГРАФИЧЕСКИХ РЕГИСТРИРУЮЩИХ СРЕД
Необходимость описания сложного процесса фотоиндуцированного фазового перехода между различными состояниями вещества при фотографической регистрации привела к эмпирической разработке классической сенситометрии [1,2]. За более чем вековую историю сенситометрия, сформулированная в 1890 г. Ф. Хертером и Д.Дриффильдом, показала свою эффективность в теории и технологии фотографического процесса [1-9]. Общая задача сенситометрии состоит в определении зависимости величины фотографического и/или голографического эффекта от параметров оптического излучения, используемого для экспонирования светочувствительного материала. Решение задачи считается полным, если результат сенситометрического испытания позволяет предсказать результат экспонирования (записи) по заданным параметрам действующего облучения [10]. Исторический опыт фотографии показал, что разработка сенситометрической системы, адекватно описывающей процесс фотографической регистрации даже на одном типе материала - галоидосеребряной эмульсии, практически невозможна [10-14].
Ситуация с регистрирующими средами оказалась еще сложнее из-за чрезвычайно широкого разнообразия первичных механизмов, используемых для регистрации оптической информации [14-16]. Так, оказалось невозможным ввести даже критерии светочувствительности, применимые ко всем светочувствительным средам независимо от механизма записи [17]. Поэтому в любом конкретном случае выбор оптимальной регистрирующей среды является серьезной научно-технической проблемой из-за отсутствия сравниваемых критериев. Аналогичная проблема продолжает существовать и в фотографии, где принципиально невозможно перейти, например, от сенситометрической системы ASA к системе DIN, ГОСТ, ХиД и др. [10-13].
Рассмотрим один из вариантов сенситометрического описания процесса голографической фазовой регистрации на пленочном носителе. Возможность использования для топографии сенситометрического описания, аналогичного классической фотографической сенситометрии, связана с двумя обстоятельствами [17]: во-первых, при малых экспозициях выполняется условие линейности:
ДЭ 1/2 ~ It, (1)
где ДЭ - дифракционная эффективность "элементарной" голограммы в виде синусоидального распределения интенсивности экспонирующего излучения, I - средняя по площади голограммы плотность интенсивности падающего излучения, t- время экспонирования. Во-вторых, при малых амплитудах фотоиндуцированной модуляции коэффициентов поглощения и преломления ДЭ как толстых (объемных), так и тонких синусоидальных амплитудно-фазовых голограмм с достаточной точностью описывается математически подобными выражениями [18, 19]. Слои дихромированного желатина, например, принято считать чисто фазовой регистрирующей средой, обеспечивающей значительные фотоиндуцированные изменения показателя преломления и толщины слоя, что приводит к большим значениям фазовой модуляции или фазового рельефа Δφ. Θменно большие значения Δφ, βызывающие сильно осциллирующее поведение зависимости ДЭ от энергии экспозиции и отсутствие описания процессов синтеза и проявления, привели к невозможности сопоставления и сравнительного анализа многочисленных экспериментальных результатов в области исследования хромированных коллоидов для голографии.
Рассмотрим процесс дифракции когерентного излучения на фазовой синусоидальной тонкой дифракционной решетке [20], определяемой коэффициентом амплитудного пропускания: вдоль оси х:
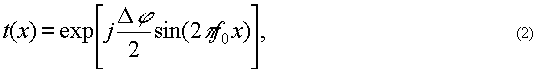
где соответствующим выбором начальной фазы исключен множитель, представляющий среднюю по решетке фазовую задержку, f0 - пространственная частота решетки с периодом dx, f0 = dx-1.
Параметр Δ φ ξпределяет разность между максимальным и минимальным значениями фазового сдвига. В сенситометрическом смысле параметр Δφ ξписывает фотографический эффект, обусловленный определенной энергией экспозиции. В случае если период решетки достаточно мал и f0 >> 1 , то непосредственное измерение величины Δφ δостаточно затруднительно либо невозможно и поэтому целесообразно перейти к другому экспериментально определяемому параметру - дифракционной эффективности - ДЭ.
Если решетка с пропусканием (2) освещается нормально падающей плоской световой волной единичной амплитуды, то, используя тождество
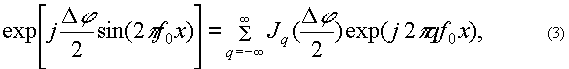
где Jq(x) - функция Бесселя первого рода q-гo порядка, можно записать амплитуду поля в зоне Фраунгофера в виде
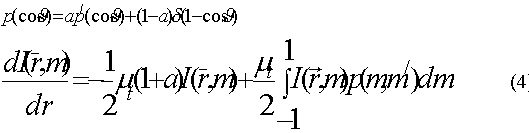
где (x0, y0) - координаты в плоскости наблюдения, l - размер решетки в направлении, перпендикулярном к ее штрихам, z - расстояние от решетки до плоскости наблюдения, k=2π/λ, λ - длина волны излучения. Если f0 >>2/ l, то перекрытия различных дифракционных порядков не происходит и распределение интенсивности в плоскости наблюдения описывается выражением:
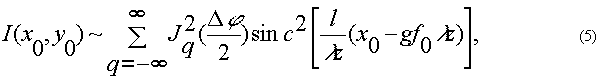
а ДЭ соответствует:

где ДЭ q - описываег эффективность дифракции в максимуме с номером q. При освещении фазовой дифракционной решетки под углом или гауссовым пучком xapaктер зависимостей (6) качественно не изменяется [17] и приводит к аналогичным функциональным зависимостям.
Из уравнения (6) следует, что при дифракции на тонкой (толщина <<f 0-1 ) фазовой дифракционной решетке энергия излучения перераспределяется между множеством дифракционных составляющих не нулевого порядка. ДЭq (для составляющей q-го порядка) определяется величиной Jq2 (Δφ/ 2). Ηависимость ДЭ от величины Δφ θмеет осциллирующий характер в соответствии со свойствами функции Бесселя. Поэтому, в общем смысле, величина ДЭ не может являться истинной сенситометрической величиной в отличие от Δφ , οоскольку для нее зависимость от энергии экспозиции будет иметь многозначный характер.
Для однозначного восстановления Δ φ по измерению величины ДЭ можно использовать различные способы. В [21] предлагается использовать измерение ДЭ для различных длин волн считывающего излучения. В принципе, измеряя эффективность для различных порядков - q - можно также восстановить значение Δφ. Ξднако в реальных фазовых регистрирующих средах при записи голограмм, как правило, происходит не только увеличение Δφ . χто описывается уравнением (2.2), но и нелинейное изменение синусоидального профиля фазового рельефа на другую, более сложную форму. Так, например, в случае дихромированного желатина фазовый профиль решетки формируется за счет изменения показателя преломления слоя (внутренний рельеф) и изменения его геометрической толщины (внешний или поверхностный рельеф), причем механизмы их образования могут значительно отличаться друг от
друга [22 ]. Также ДЭ сильно зависит от геометрии записи и считывания - при переходе от тонкой голограммы к объемной происходит изменение функционального вида ДЭ [18].
При амплитудной записи интерференционной картины о появлении нелинейных эффектов свидетельствует возникновение при дифракции излучения на проявленной тонкой голограмме дифракционных порядков выше первого. В случае фазовой синусоидальной решетки число порядков дифракции почти всегда достаточно велико. Оценим поэтому максимальное число порядков дифракции, соответствующих начальному участку роста ДЭ, т.е. той области изменений Δ φ, κогда величина ДЭ может использоваться как сенситометрический параметр, однозначно связанный с Δφ.
Используя известное интегральное представление для функции Бесселя [23]
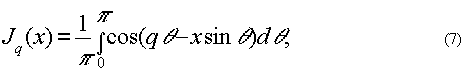
можно считать, что дифракционные порядки, соответствующие значениям q > qmax, имеют нулевую интенсивность, если аргумент
подинтегральной функции достаточно велик и сама подинтеграль-ная функция сильно осциллирует. Этому соответствует неравенство
qmax θ -xsinθ>>1 (8)
или
qmax >>xsin θ
Если значение x=x1m соответствует первому максимуму
I1(x1m = 1,8) = 0,5815, то, принимая в качестве грубой оценки
(sinQ = 1 или Q = π/2, получим
qmax π/2 >> x1m, или qmax >> 2x1m/π. (9)
Поскольку x1m = Δφ/2 = 1.8. то можно полагать, что равны нулю все порядки с qmax>3. Имея в виду приблизительный характер проведенных оценок, можно считать, что если при дифракции на решет-
ке с фазовым рельефом Л(р возникает не более 11 (±5) порядков, то имеется взаимно однозначное соответствие между ДЭ и Л(р и отсутствует сильная нелинейность при записи или, иными словами, фазовый рельеф является синусоидальным. В соответствии с [24]:
J2(1,8): J3(1,8): J4(1,8):J5(1,8):J6(1,8) =
=0,306: 0,098: 0,023: 0,0043: 0,0006, (10)
что подтверждает справедливость предложенного критерия.
Дифракционные решетки, полученные голографическим способом и применяемые для мультипликации изображений [35,26], принято описывать параметром их степени мультипликации
М = 2q max+1, (11)
где qmax - максимальный номер наблюдаемого порядка дифракции. Имея в виду зрительное обнаружение порядка дифракции, можно принять, например, за порог обнаружения величину 0,1% от интенсивности падающего на решетку излучения. Явным удобством параметра (11) является легкость его определения по дифракции лазерного пучка на исследуемой решетке. С учетом (11) и введенного критерия условие (9) можно переписать в виде

где m - число порядков дифракции в одну сторону от центрального максимума (q=O), далее называемое кратностью мультипликации.
Таким образом, для голографической сенситометрии фазовых регистрирующих сред можно использовать следующие параметры:
Δφ - β еличина фазовой модуляции слоем регистрирующей среды, измеренная путем непосредственной визуализации в интерферометре Маха-Цендера или Линника (МИИ-4, МИИ-12), или ДЭ - дифракционная эффективность на начальном участке Δφ (δо достижения первого максимума ДЭ) при одновременном контроле степени линейности записи путем определения параметра m. Для обеспечения однозначности зависимости ДЭ от Δφ κратность мультипликации не должна превышать значения mmax=5.
Сопоставительный анализ результатов, измеренных по визуализации фазового рельефа Δ φ ρ помощью интерферометра и измеренных для этих же решеток величин ДЭ, показал удовлетворительное совпадение получаемых данных, по крайней мере, с точностью, достаточной для технологических целей.
Другие сенситометрические параметры типа энергии экспозиции, интенсивности записывающего излучения, характеристик явления невзаимозаместимости (НВЗ) соответствуют классической фотографической сенситометрии [2,10,11]. По сложившейся традиции графическое представление результатов приводится в логарифмическом масштабе. Светочувствительность в каждом конкретном случае определяется либо по уровню порогового фотографического эффекта, либо как точка инерции [11,12] для соответствующей характеристической кривой.
Литература
1. Чибисов К.В. Очерки по истории фотографии. М.:Искусство, 1987. 255с.
2. Чибисов К.В. Общая фотография (Фотографические процессы регистрации информации). М.: Искусство, 1984. 446 с.
3. Клепиков П.В. Позитивные процессы на солях хрома. М.:
Госкиноиздат, 1938. 128с.
4. Миз К., Теория фотографического процесса. М.-Л.: Гос. изд-во техн.-теор. лит-ры, 1949. 732 с.
5. Миз К., Джеймс Т. Теория фотографического процесса. Л.:Химия, 1973.576с.
6. Джеймс Т.Х. Теория фотографического процесса. Л.: Химия, 1980.672с.
7. Джеймс Т., Хиггинс Дж. Основы теории фотографического процесса. М.: Изд-во иностр. лит, 1954. 288 с.
8. Чибисов К.В. Химия фотографических эмульсий. М.: Наука,
1975. 344с.
9. Чибисов К.В. Природа фотографической чувствительности. М.:
Наука,1980. 378 с.
10. Зернов В.А. Фотографическая сенситометрия. М.: Искусство,
1980. 351 с.
11. Михайлов В.Л. Свойства и применение светочувствительных материалов. М.: Госкиноиздат, 1938. 128с.
12. Шашлов Б.А., Шеберстов В.И. Теория фотографических процессов. М.: МГАП "Мир книги", 1993. 312 с.
13.Варгафтич М.Г. Кино - фото - материаловедение. М.: Госкино-издат, 1939. 300 с.
14.Бетхер X., Эпперляйн И., Ельцов А.В. Современные системы регистрации информации. СПб: Синтез, 1992. 328 с.
15. Несеребряные фотографические процессы/ Под ред. А.Л. Кар-тужанского. Л.: Химия, 1974. 376 с.
16. Несеребряные и необычные среды для голографии/ Под ред.
В.А. Барачевского. Л.: Наука, 1978. 286 с.
17.0золс А.О., Шварц К.К. Критерии светочувствительности сред
и оптимизация записи голограмм // Квантовая электроника.
1982. Т.9. № 12. С. 2441-2448.
1 8.Кольер Р.,Беркхардт К., Лин Л. Оптическая голография. М.:
Мир, 1975.686с.
19. Оптическая голография/ Под ред. Г. Колфилда. В 2-х т. М.:
Мир, 1982.
20.Гудмен Дж. Введение в Фурье-оптику. М.: Мир. 1970. 364 с.
21.Стринадко Л.В., Тарновецкий В.В., Стринадко М.Т., Андреев Ю.С., Полянский В.К. Метод определения параметров фазового оптического рельефа, записанного на фотографическом слое // Журнал научи. и прикл. фотографии и кинематографии. 1979. Т.24. № 3. С. 219-222.
22.Ерко А.М., Малов А.Н. Оптимизация параметров обработки слоев дихромированного желатина для записи оптической информации// Журнал научн. и прикл. фотогр. и кинематографии. 1980. Т.25.№З.С.185-187.
23.Папулис А. Теория систем и преобразований в оптике. М.:Мир, 1971.496с.
24. Справочник по специальным функциям/ Под ред. М.Абрамовича и И.Стиган. М.: Наука,1979. 832 с.
25.Boivin L.P. Multiple imaging using varies types of simple phase gratings// Appl. Opt., 1972. V.I 1. P. 1782-1792.
26. Kalestynski A., Smolinska B. Self-restoration and autoidolon of defective periodic objects// Optica Acta. 1978. V. 25. № 2. Р. 125-134.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

