П.А.ВЕРБЛЮДЕНКО, Э.Е. СОН
ВОССТАНОВЛЕНИЕ ИЗОБРАЖЕНИЙ В ЛАЗЕРНОЙ МЕДИЦИНСКОЙ ТОМОГРАФИИ
Введение
Данная работа посвящена проблеме восстановления изображений в лазерной медицинской томографии. Осуществлено по строение схемы сканирования и фантома для компьютерного моделирования. Представлен пакет программ для восстановления изображений матричным алгоритмом. С его помощью восстановлены несколько фантомов со значениями плотности, соответствующими реальным биотканям. Проверено влияние на качество реконструкции перепадов плотностей, пространственного расположения неоднородностей. Для улучшения качества реконструкции предложен метод масштабирования исходных данных.
Изучение распространения света в биотканях позволяет получить данные, которые используются для многочисленных медицинских и биомедицинских приложений лазеров и других источников света. Характеристики поглощения и рассеяния света определяют его пространственное распределение в облучаемой ткани и соответствующий биологический эффект, который используется в лазерной хирургии и для терапевтических целей. Для целей диагностики, например для неинвазивной оптической спектроскопии мозга, груди, мышц и других тканей, измерения характеристик прошедшего света дают возможность определить метаболические, физиологические и структурные изменения тканей [1]. Все клинические приложения такого "дистанционного зондирования" основаны на извлечении информации о поглощении и рассеянии ткани неинвазивными измерениями интенсивности (спектра) диффузионно-отраженного или диффузионно-прошедшего света. Эти оптические свойства в свою очередь связаны с функционированием или структурой ткани.
Основное направления дальнейшего развития оптических методов диагностики - получение высокоточных изображений внутренних органов. Ведутся работы по созданию такой аппаратуры в ближнем инфракрасном диапазоне по аналогии с изображением, получаемым с помощью рентгеновского томографа [2]. Исследуют-
ся в основном ткани груди и мозг. Работа по созданию аппаратуры, восстанавливающей изображения внутренних органов и тканей по информации о прошедшем лазерном излучении, требует совер-шенствования математического аппарата решения обратной задачи прохождения лазерного излучения через ткань. Действительно, из-за сильного рассеяния лазерного излучения биотканями данная задача представляется значительно более сложной, нежели обратная задача, решаемая в рентгеновской томографии.
В данной работе для решения обратной томографической задачи предложен алгоритм, основанный на дискретизации восстанавливаемого изображения и решении уравнений Эйлера - матричный топографический алгоритм.
Математическая модель
В общем случае нестационарного светового поля с произвольно заданными источниками уравнение переноса излучения без учета состояния поляризации светового пучка имеет вид [6]:
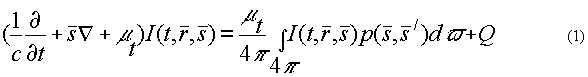
индикатрисса рассеяния здесь удовлетворяет условию нормировки:
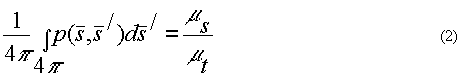
Характерная длина лазерного импульса, которая возникает в топографических задачах 10-12 - 10-6 с, т.е. характерный размер меняется в пределах 10-4 – 102 м. Размер человеческого тела порядка 1 м. Ясно, что при импульсах длиной 10-12–10-8 с задача существенно нестационарна. Положим, что в нашем случае импульс имеет достаточную длину для того, чтобы считать задачу стационарной, а внутренние источники отсутствуют.
Благодаря сильной вытянутости индикатриссы рассеяния и существенному отличию вероятности выживания фотона от единицы световой пучок в биотканях проходит достаточно большой путь, сохраняя высокую степень направленности. Это обстоятельство дает возможность перейти в уравнении (1) к малоугловому приближению:
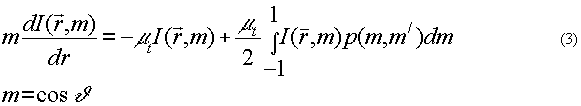
Высокая направленность индикатриссы дает основание для перехода в правой части (3) к транспортному приближению (дельта-приближение индикатриссы):
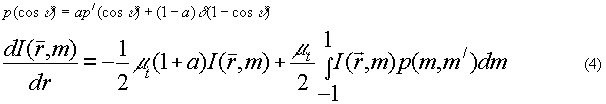
Воспользуемся простейшим вариантом транспортного приближения и положим p'=1, a a=l-g, тогда
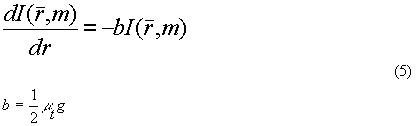
Таким образом, исходное уравнение переноса (1), вообще говоря нелинейное относительно оптических коэффициентов изучаемой нами биоткани, сведено к уравнению (5) с использованием малоуглового и транспортного приближений.
Дискретизация
Разобьем восстанавливаемое изображение на ячейки. Для определенности представим наше изображение в виде квадрата, разбитого на ячейки как на рисунке 1. Оптическая плотность изображения представится в виде вектора b, где bj - оптическая плотность j-й ячейки (см.(5)). Тогда основное уравнение компьютерной томографии можно представить в виде произведения матричных операторов:
Rij*bj=ui или R*B=U (6)
Здесь R - это матрица сканирования - элемент Rij равен расстоянию, которое i-я прямая сканирования проходит в j-й ячейке изображения; ui - это обработанная информация о прошедшем излучении полученная от i-й прямой сканирования. Если матрица сканирования известна нам с точностью h, а правая часть u с точностью d, то можно воспользоваться тем [7], что решение b,
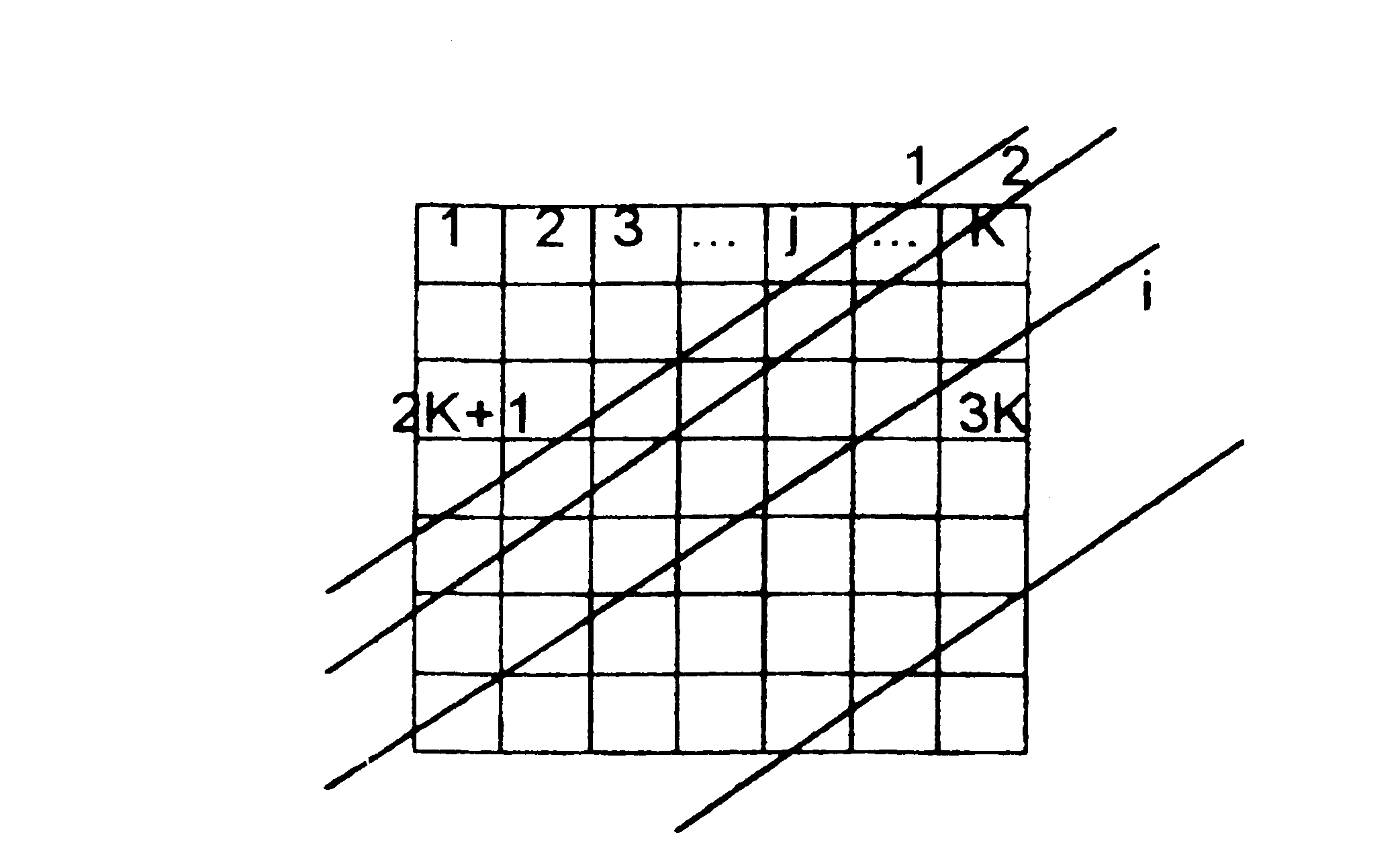
Рис. 1. Дискретизация исходного изображения: общее количество ячеек - N=K * К, общее количество прямых сканирования - М
которое минимизирует регуляризующий функционал в соответствии с принципом регуляризации Тихонова [9], удовлетворяет уравнению Эйлера:
R*hRhB-R*hUd+aB=0 (7)
Таким образом приходим к системе уравнений:
AaB=AB+aCB=F (8)
Для решения системы линейных уравнений (8) можно использовать различные численные методы [5, 7-9]. При этом следует учитывать, что матрица Аa системы является симметричной и положительно определенной. Это позволяет использовать дня решения (8) очень эффективные специальные методы. Параметр а выбирается по невязке.
Предложенный метод реконструкции не требует представления основного уравнения томографии в интегральном виде, его можно применять для широкого спектра схем сканирования, например, сканирования вдоль кривых или даже по площадям, данный метод представляется устойчивым к уровню шумов в начальных данных и неоднородностям восстанавливаемого изображения.
Существенным недостатком метода можно считать значительный объем вычислений, что сопряжено с большими затратами машинного времени и памяти.
Схема сканирования. Фантом
В настоящее время в медицинской компьютерной томографии известно несколько типов аппаратной реализации сканирования объекта. Выберем одну из этих схем, в которой источник и детектор излучения движутся перпендикулярно прямой, соединяющей их, при каждом угле поворота системы источник-детектор относительно исследуемого объекта. Каждая прямая сканирования в соответствии с уравнением прямой:
х cosj + у sinj = p (9)
характеризуется двумя параметрами - расстоянием от начала координат до прямой - р и углом j между осью ОХ и нормалью к прямой из центра координат. Общее количество прямых сканирования - М, причем их число не должно быть меньше, чем количество ячеек восстанавливаемого изображения - N. Шаг по j выбран равномерным из расчета ≥ N/2 узлов в сетке пo j. Для того, чтобы все прямые сканирования проходили через исследуемый объект и не было бы случаев прохождения прямой "мимо" объекта, шаг по р должен быть согласован с углом наклона прямой j. Если характерная длина восстанавливаемого изображения равна D, то для i-й прямой сканирования максимальная величина параметра р равна:
pi = D / cosji Шаг выбирается равномерно из расчета ≥ N/2 узлов в сетке по р.
Расчет матрицы сканирования в соответствии с предложенной схемой сканирования осуществлен в программе MATRIX. Описанная схема сканирования проста в реализации как аппаратной, так и программной и обеспечивает получение достаточного количества информации для успешного восстановления исследуемого изображения. Основным недостатком предложенной схемы является достаточно большое (до нескольких минут) время сканирования, что достаточно велико для обследования движущихся органов (например, легкого или сердца). В настоящее время разработаны более прогрессивные схемы сканирования, где за счет большого количества источников и приемников излучения время сканирования снижено до 0.01 - 1 секунды. Поскольку матричный томографический алгоритм допускает использование широкого спектра схем сканирования, все прогрессивные схемы сканирования с малыми временами обследования могут быть успешно реализованы с его помощью.
Построению
алгоритмов восстановления изображений объектов по реально
измеренным данным сканирования должно пред-шествовать восстановление
математически смоделированных изображений. Это позволяет
оценить качество алгоритма исследовать его поведение в различных,
часто не реализуемых на тактике условиях, смоделировать
влияние на алгоритм отдельных явлений которые встречаются
на практике только в совокупности Для этой цели был разработан
и построен фантом, т.е. изображение на котором проводились
испытания матричного алгоритма реконструкции.
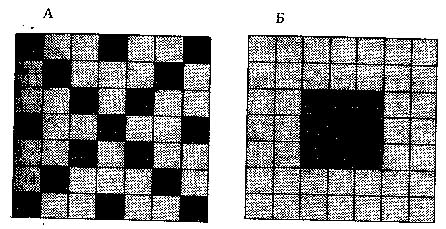
Рис. 2. Фантом размерностью 7*7= 49 ячеек
Основной принцип построения фантомов - это разбиение воображения на ячейки, в данном случае на квадраты, и усреднение плотности изображения в каждой такой ячейке. Был разработан фантом (см. рис.2) размером 7*7=49 ячеек. Соответствующая ему матрица сканирования имеет размерность 49*49=2.401 и успешно обрабатывается на простейших ЭВМ. Отдельным ячейкам фантома присваивались различные значения, что дало возможность исследовать матричный алгоритм на разрешение и чувствительность к большим перепадам плотности от ячейки к ячейке.
Результаты расчетов
Описанные в предыдущих разделах матричный алгоритм восстановления изображения, схема сканирования и фантомы были
реализованы в программе ALEF. Время расчета составляло около пятидесяти секунд. В качестве фантомов использовались фантомы А, Б (см. рис. 2). Уровень шумов в операторе принимался равным h=10-5 а в правой части d=10-4.
Значения плотностей ячеек фантома выбирались из следующих соображений: моделировалась среда, которая соответствует головному мозгу. В соответствии с формулой (5) для создания фантома необходима информация о коэффициенте ослабления и показателе анизотропии, которые можно взять из обзора [4]. Таким образом возьмем следующие показатели тканей головного мозга:
белое вещество - mt=52.6 см-1, g=0.96 см-1
серое вещество - mt=62.8 см-1, g=0.88 см-1
глиома - mt=250 см-1, g==0.9 см-1 (эти параметры вычислены приблизительно на основании данных о показателе поглощения глиомы).
Основная часть фантома будет состоять из белого вещества (светлые клетки на фантомах А, Б). На этом фоне располагаются вкрапления и области либо из серого вещества, которое слабо отличается по плотности от белого (на 4%), либо из ткани глиомы, которая согласно представленной модели отличается от него сильно (в 5 раз) (темные клетки на фантомах А-Г). Это дает возможность испытать предложенный алгоритм на чувствительность как к большим, так и к малым перепадам плотности фантома. По формуле (5) в соответствии с транспортным приближением вычисляем плотность указанных тканей в условных единицах: bБВ=27.4, bСВ=35.8, bГ==139. На рис. 3,4 представлены результаты расчетов программы ALEF по восстановлению изображения фантомов.
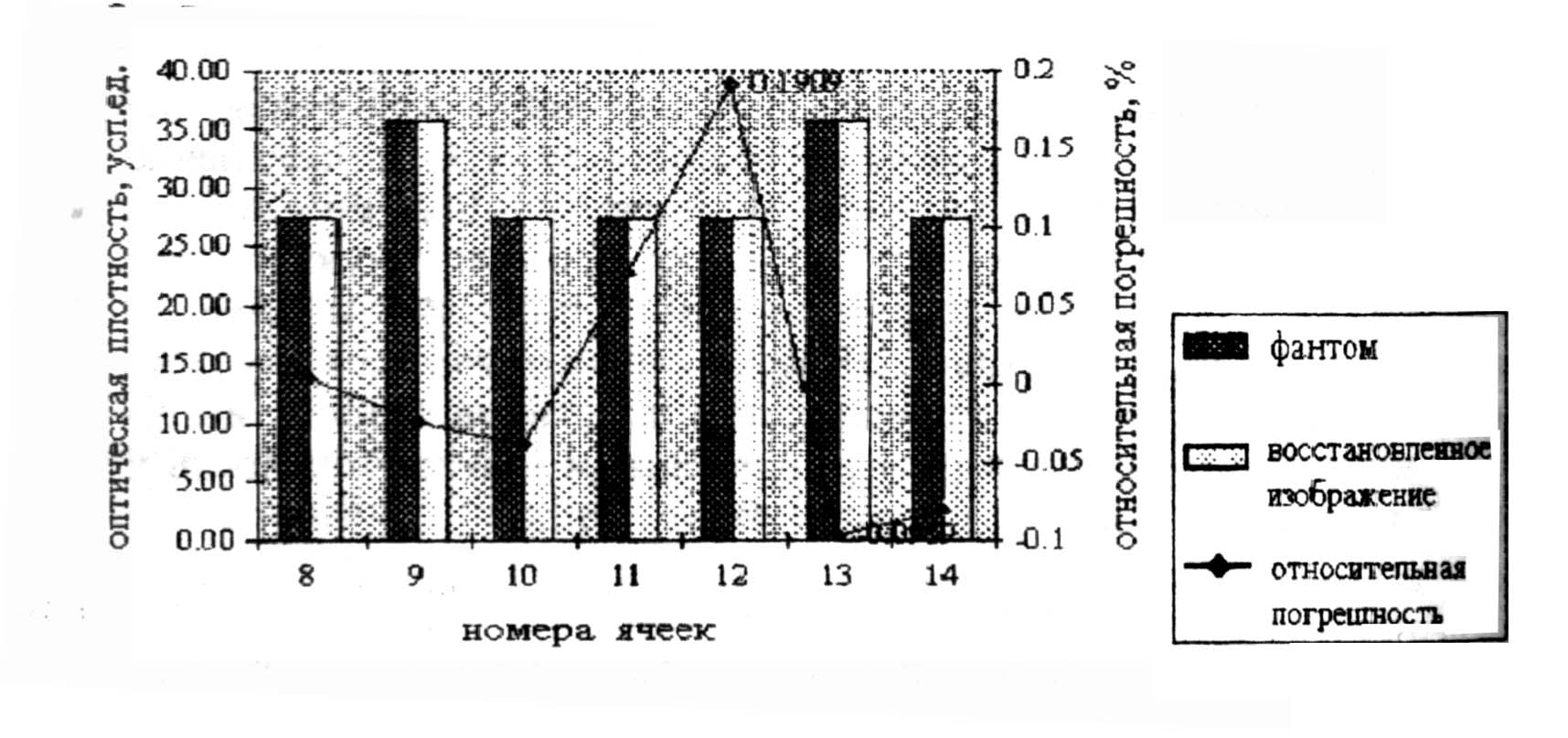Рис.3. Восстановление фантома А.Строка два.
Проверка разрешения при слабых изменениях плотности
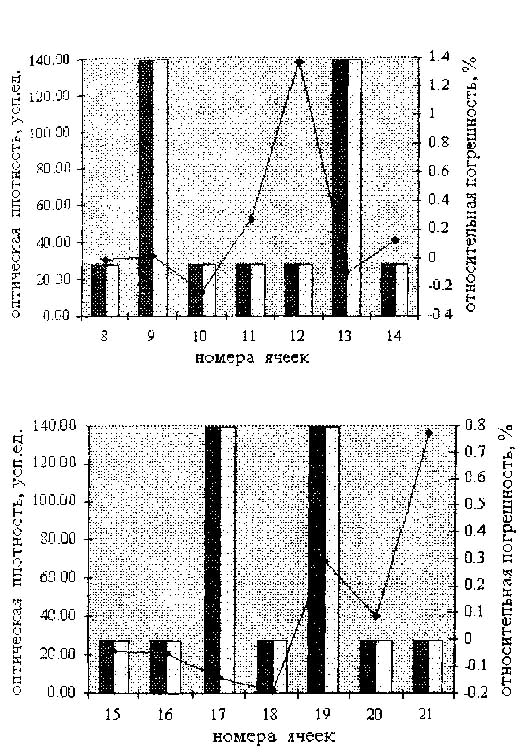Рис.4.
Восстановление фантома А. Строка два и три.
Проверка разрешения при сильных изменениях плотности
Рисунки 3-4 демонстрируют расчеты, в которых неоднородности разной величины размешались на разных расстояниях
друг от друга. В общем случае чем меньше неоднородность, тем меньше средняя погрешность - на рис. 3 она составляет 0.07%, в то время как для больших неоднородностей на рис. 4 - 0.25%. А вот расстояние между неоднородностями на погрешности не влияет, их средняя величина неизменно близка к 0.25%.
Заметим, что получившийся уровень погрешностей чрезвычайно низок. По рисункам не видно никакой связи между уровнем погрешностей и распределением плотности по фантому, что наводит на мысль о том, что эти погрешности определяются в основном не физическими особенностями фантома, а свойствами вычислительной схемы.
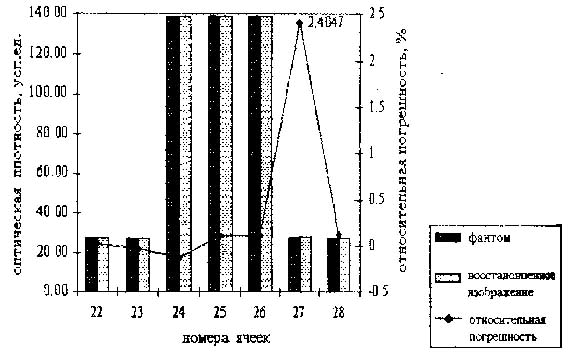На
рисунке 5 неоднородность в виде "плато", в этом случае погрешности
наибольшие, их средняя величина - 0.4%.
Рис. 5. Восстановление фантома Г. Строка четыре. Проверка на погрешности на границах "уступа"
Сравнивая рисунки 3-5, нетрудно заметить, что уровень по-грешностей всегда больше к концу рассматриваемого ряда ячеек фантома. Пока уровень погрешностей настолько мал, что не пре-восходит 1%, эта особенность расчетной схемы несущественна, но при больших погрешностях она, возможно, окажет на решение какое-то влияние.
Поскольку, как уже упоминалось, основная причина погорим подобнее особенности paсчетной схемы,связанные с масштабом величин, выбранных для расчетов. Для этого уменьшим исходные величины bБВ, bСВ, bГ последовательно в 10, 100, 1000 и 10000. Результаты такого выбора исходных данных показаны на рис.6.
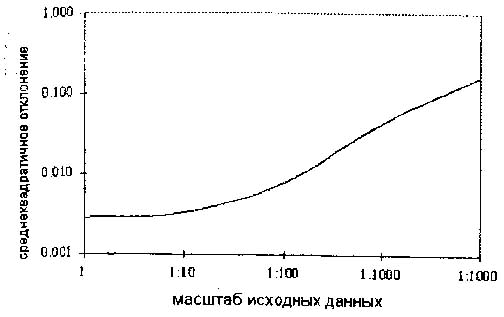
Рис. 6. Фантом Г. Рост среднеквадратичной ошибки в восстановленном изображения при уменьшении масштаба исходных данных о распределении плотности в фантоме
На рис. 6 представлен график среднеквадратичных отклонений по фантому Б. Видно, что уменьшение масштаба оказывает катастрофическое воздействие на погрешности: в случае масштаба 1:1000 среднеквадратичное отклонение достигает 0.05, а в случае 1:10000даже 0.1. По- видимому, это связано с тем, что при маленьких значениях b матрицы, над которыми проводятся вычисления, становятся плохо определенными, что сказывается на эффективности всего матричного алгоритма. Это обстоятельство подсказывает способ улучшения качества работы алгоритма - масштабирование исходных данных.
Итак, по итогам численных расчетов можно сделать вывод о том, что предложенный матричный алгоритм обладает высокой точностью, достаточным разрешением и может с успехом использоваться для восстановления изображений в медицинской томографии.
Выводы
Данная работа посвящена проблеме восстановления изображений в лазерной медицинской томографии.
Осуществлено построение схемы сканирования и фантома для компьютерного моделирования. Представлен пакет программ для восстановления изображений матричным алгоритмом. С его помощью восстановлены несколько фантомов со значениями плотности, соответствующими реальным биотканям. Проверено влияние на качество реконструкции перепадов плотностей, пространственного расположения неоднородностей. Для улучшения качества реконструкции предложен метод масштабирования исходных данных. Сделан вывод о том, что матричный алгоритм способен обеспечить высокое качество томограммы.
Необходимо развивать предложенный матричный алгоритм дальше. Главное направление работы видится в совершенствовании математической модели прохождения излучения, в выборе модели, более полно описывающей индикатриссу и рассеяние.
Литература
1. Приезжев А.В., Тучин В.В, Шубочкин Л.П. Лазерная диагностика
в биологии и медицине. М.: Наука, 1989.
2. Hebden J.C., Wong K.S. Time-resolved optical tomography // Applied Optics. 1993.V.32. N. 4. P. 372-380.
3. Тихонов А.Н., Арсенин В.Я., Тимонов А.А. Математические задачи компьютерной томографии. М.: Наука, 1987.
4.. Cheong W., Prahl S. A., Welch A. J. A Review of the Optical Properties of Biological Tissues // IEEE Journal of Quantun Electronics. 1990. V.12, P. 2166-2185.
5. Хермен Г. Восстановление изображения по проекциям. Основы
реконструктивной томографии/ Пер. с англ. М.: Мир, 1983. 349 с.
6. Исимару А. Распространение и рассеяние волн в случайно-неоднородных средах. М.: Мир, 1981.
7. Тихонов А.Н., Гончарский А.В., Степанов В.В., Ягола А.Г. Чис-ленные методы решения некорректных задач. М.: Наука, 1990.
8. Тихонов А.Н., Гончарский А.В., Степанов В.В., Ягола А.Г. Регу-ляризирующие алгоритмы и априорная информация. М.: Наука, 1983.200 с.
9. Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. М.: Наука, 1979. 285 с.
