|
|
 |
 |

|
| |
Е.Г.АБРАМОЧКИН, В.Г.ВОЛОСТНИКОВ, М.Ю.ЛОКТЕВ.
ВОССТАНОВЛЕНИЕ СВЕТОВЫХ ПОЛЕЙ ПО
ИЗМЕРЕНИЯМ ИНТЕНСИВНОСТИ В ЗОНЕ
ФРЕНЕЛЯ
В настоящее время в оптике наряду с используемыми для получения информации о фазе светового поля методами интерферометрии и голографии представляют практический интерес и него-лографические методы. Это связано с невозможностью реализовать в ряде случаев голографический принцип; кроме того, часто требуется раздельный анализ амплитудной и фазовой информации. В связи с этим за последние два десятилетия повысился интерес к так называемой фазовой проблеме - проблеме восстановления фазы светового поля по его энергетическим характеристикам. В этом случае для восстановления фазы требуются два измерения интенсивности в двух близких параллельных плоскостях в зоне дифракции Френеля. В работе приведены результаты численных экспериментов, причем используемый алгоритм показал высокую устойчивость к шумам детектирования. Восстановление фазы путем реализации аналитического продолжения одномерной функции в комплексную плоскость оптическими методами.
Рассмотрим следующую постановку задачи. Пусть U(x) - комплексная амплитуда светового поля в плоскости объекта, ограниченного апертурой [а, b]. Тогда комплексная амплитуда поля в некоторой плоскости, находящейся на расстоянии l от исходной, определяется формулой:
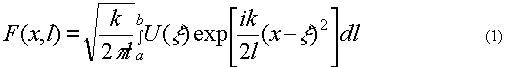
Как показано в работе [I], одно измерение интенсивности в плоскости l не позволяет восстановить исходное поле; для этого необходимо провести дополнительные измерения интенсивности либо использовать априорно известную информацию о поле. Исследуемый метод, описанный ранее в работе [2], основан на реше-
нии параксиального параболического уравнения для светового поля [3]:
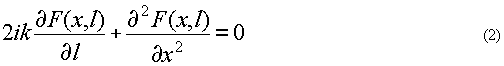
Выразив F(x,l) через интенсивность и фазу: 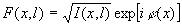 , получим , получим

После двукратного интегрирования по х получим выражение для фазы поля в зоне Френеля с точностью до произвольной постоянной:
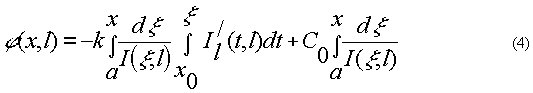
Здесь 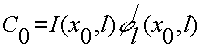 . Таким образом, можно восстановить фазу поля, зная распределение интенсивности и производной . Таким образом, можно восстановить фазу поля, зная распределение интенсивности и производной 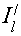 в некоторой плоскости. Кроме того, нужно знать граничное условие для производной фазы в некоторой плоскости. Кроме того, нужно знать граничное условие для производной фазы 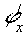 в некоторой точке x0 . Как показано в в некоторой точке x0 . Как показано в
работе [2], его можно получить из измерений интенсивности, используя ее аналитическое продолжение в комплексную плоскость z = х + iy:
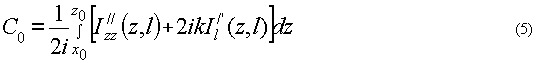
где z0 =x0 + iy0 - нуль аналитического продолжения комплексного поля F(z,l). Отметим, что аналитическое продолжение интен-
сивности 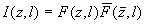 имеет два сопряженных нуля - имеет два сопряженных нуля - 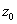
и 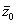 , из которых , из которых 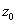 принадлежит F(z,l) , a принадлежит F(z,l) , a 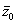 - - 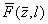 . Отметим, что только в случае, когда верхний предел интегрирования в (5) равен z0, интеграл в (5) принимает вещественное значение, благодаря этому мы можем из этой пары выделить нуль, принадлежащий F(z,l). . Отметим, что только в случае, когда верхний предел интегрирования в (5) равен z0, интеграл в (5) принимает вещественное значение, благодаря этому мы можем из этой пары выделить нуль, принадлежащий F(z,l).
В случае, когда z0 = х0 - вещественный нуль, выражение (4) можно привести к виду:
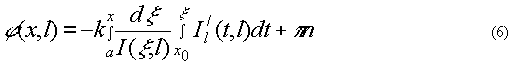
где n - число вещественных нулей на интервале [а,х] с учетом кратности. Производную 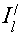 можно заменить ее разностным аналогом, измерив интенсивность в двух близких плоскостях l и l+dl: можно заменить ее разностным аналогом, измерив интенсивность в двух близких плоскостях l и l+dl:
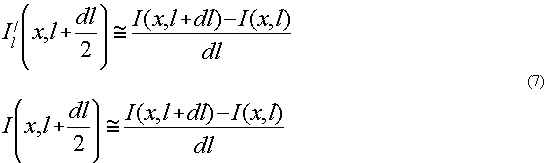
Таким образом, по измерению интенсивностей в двух плоскостях можно восстановить фазу.
Данный метод был реализован в программе, написанной на языке Turbo Pascal. Комплексные распределения были представлены в виде массивов значений в 1024 точках. Прямое и обратное преобразования Френеля реализованы с помощью алгоритма БПФ Все интегралы вычислялись по формуле Симпсона. Аналитическое продолжение функций 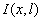 и и 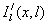 осуществлялось с помощью полиномов Ньютона [4] в окрестности глобального минимума интенсивности, так как именно в этой области нуль F(z,l) располагается ближе всего к вещественной оси. Число узлов при интерполяции выбиралось равным 20. Нуль функции I(z) находился с осуществлялось с помощью полиномов Ньютона [4] в окрестности глобального минимума интенсивности, так как именно в этой области нуль F(z,l) располагается ближе всего к вещественной оси. Число узлов при интерполяции выбиралось равным 20. Нуль функции I(z) находился с
помощью итерационного метода Ньютона решения нелинейного уравнения I(z)=0:
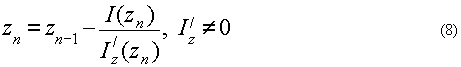
Затем с помощью аналитического продолжения 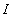 и и 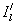 по формуле по формуле
(5) рассчитывались значения C0 для найденного и сопряженного
ему нулей I(z), а потом из двух значений выбиралось то, которое ближе всего к вещественному. После этого по формуле (4) вычислялась фаза.
Цель проведенных в данной работе численных экспериментов - оценка границ применимости описанного выше метода по l и Dl, а также исследование влияния шумов на точность восстановления фазы дальнего поля и поля в плоскости объекта. Выясним характер возникающих в ходе вычислений погрешностей. Во-первых, вследствие финитного характера дискретного преобразования Фурье возникает так называемый эффект Гиббса, который, в частности, выражается в появлении осцилляции амплитуды восстановленного поля. Существенные ошибки возникают в расчете по формулам (4)-(6) из-за неточного определения x0 (что, в свою очередь, является следствием ошибок при интерполяции). Это выражается в появлении усредненного наклона восстановленного объектного поля по отношению к исходному. Использовалось объектное поле со ступенчатой амплитудой и фазой вида 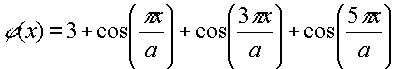 на апертуре [-а,а], на апертуре [-а,а],
где а =0.25 мм.
В первой серии экспериментов объектное поле восстанавливалось при различных значениях l. Наилучшее восстановление наблюдалось при значениях l от 20 до 450 мм, что соответствует значениям параметра l/D от 0.05 до 1.1 (среднеквадратичное отклонение амплитуды - 124
26% , фазы - 0.024
0.041) (рис. 1, с.68). Восстановление несколько ухудшилось при l от 500 до 5000 мм. (средне-квадратичное отклонение амплитуды - 204
43%, фазы - 0.084
0.191), но при этом сохранялась форма фазового профиля. Ухудшение происходило и при уменьшении l до 8 мм, а при
l > 5000 мм. и при l < 8 мм. адекватного восстановления не наблюдалось. Это согласуется с ранее проведенной теоретической оценкой [2], основанной на анализе функции корреляции между амплитудой и фазой. Отметим, что снижение информативности измерений в дальней зоне связано с тем, что распределение интенсивности становится подобным преобразованию Фурье объекта и при распространении не меняется.
Во второй серии экспериментов объектное поле восстанавливалось при фиксированном значении l = 200 мм. и меняющихся Dl. Оценка на максимально возможное значение Dl была получена ранее [2] из условия малости второго члена разложения функции I(x,l+ Dl) в ряд по Dl по сравнению с первым:

Увеличение D l от 0.1 до 5 мм. не привело к заметному ухудшению качества восстановления (среднеквадратичное отклонение амплитуды - 16 ± 18%, фазы - 0.029 ± 0.035 1). При Dl = 15 мм. качество все еще остается удовлетворительным (среднеквадратичное отклонение амплитуды - 25%, фазы - 0.072 1), а при Dl /
15 мм., что по порядку величины приближается к теоретическому пределу, резко падает.
Третья серия экспериментов проводилась с целью исследования влияния шумов на восстановление (рис.2, с.б9). Наиболее
чувствительны к шуму значения  , поэтому Dl выбиралось настолько большим, насколько позволяет теоретическая оценка. Результаты показывают, что шум J 0.3% практически не влияет на восстановление. При шуме 1% форма фазового профиля все еще воспроизводится. Таким образом, исследуемый метод показал довольно высокую устойчивость к шумам детектирования. , поэтому Dl выбиралось настолько большим, насколько позволяет теоретическая оценка. Результаты показывают, что шум J 0.3% практически не влияет на восстановление. При шуме 1% форма фазового профиля все еще воспроизводится. Таким образом, исследуемый метод показал довольно высокую устойчивость к шумам детектирования.
В заключение отметим, что аналитическое продолжение. которое обычно на практике осуществляется численными методами, можно реализовать и оптическими методами. При исследовании свойств интегрального астигматического преобразования получено следующее выражение:
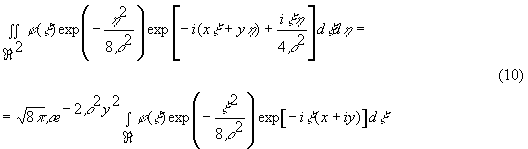
Видно, что интеграл в правой части этого выражения не что иное, как аналитическое продолжение в комплексную плоскость преобразования Фурье функции 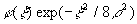 . На практике это преобразование реализуется с использованием астигматической оптики и может быть использовано для восстановления фазы по распределению нулей интенсивности полученного аналитического продолжения [I]. В настоящее время исследуются возможности этого метода. . На практике это преобразование реализуется с использованием астигматической оптики и может быть использовано для восстановления фазы по распределению нулей интенсивности полученного аналитического продолжения [I]. В настоящее время исследуются возможности этого метода.
Литература
1. Ферверда Х.А. Проблема восстановления фазы волнового фронта по амплитудному распределению и функциям когерентности // Обратные задачи в оптике. М.:Машиностроение, 1984. С. 21-41.
2. Волостников В.Г. Фазовая проблема в оптике // Препринт №93, Оптика и спектроскопия. М.:ФИАН, 1990.
3. Виноградова М.Б., Руденко О.В., Сухоруков А.П. Теория волн. М.:Наука, 1979.
4. Самарский А.А. Введение в численные методы. М.: Наука,1979.
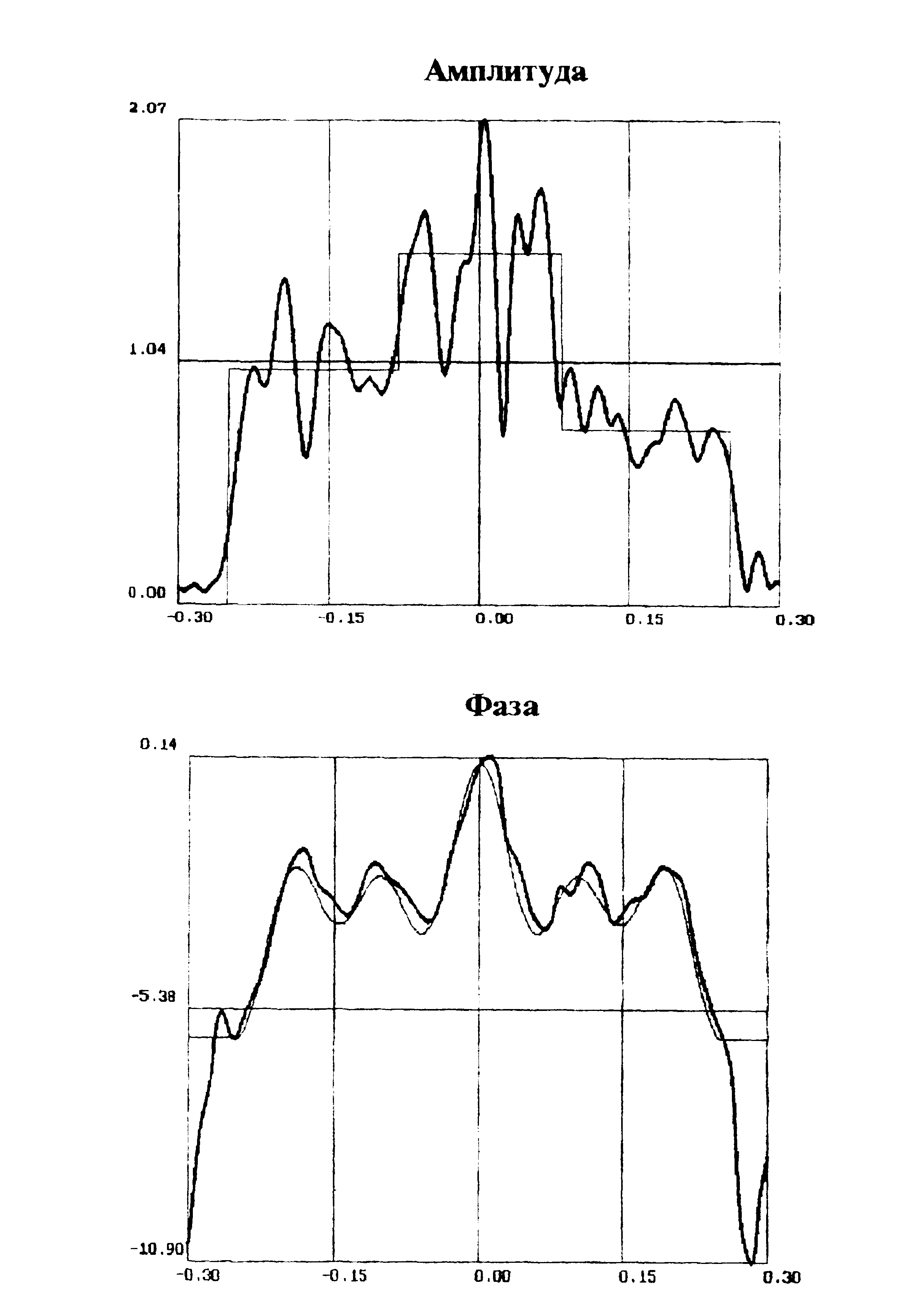
Рис .1. Исходное и восстановленное объектное поле при l = 80 мм. и Dl = 0.5 мм
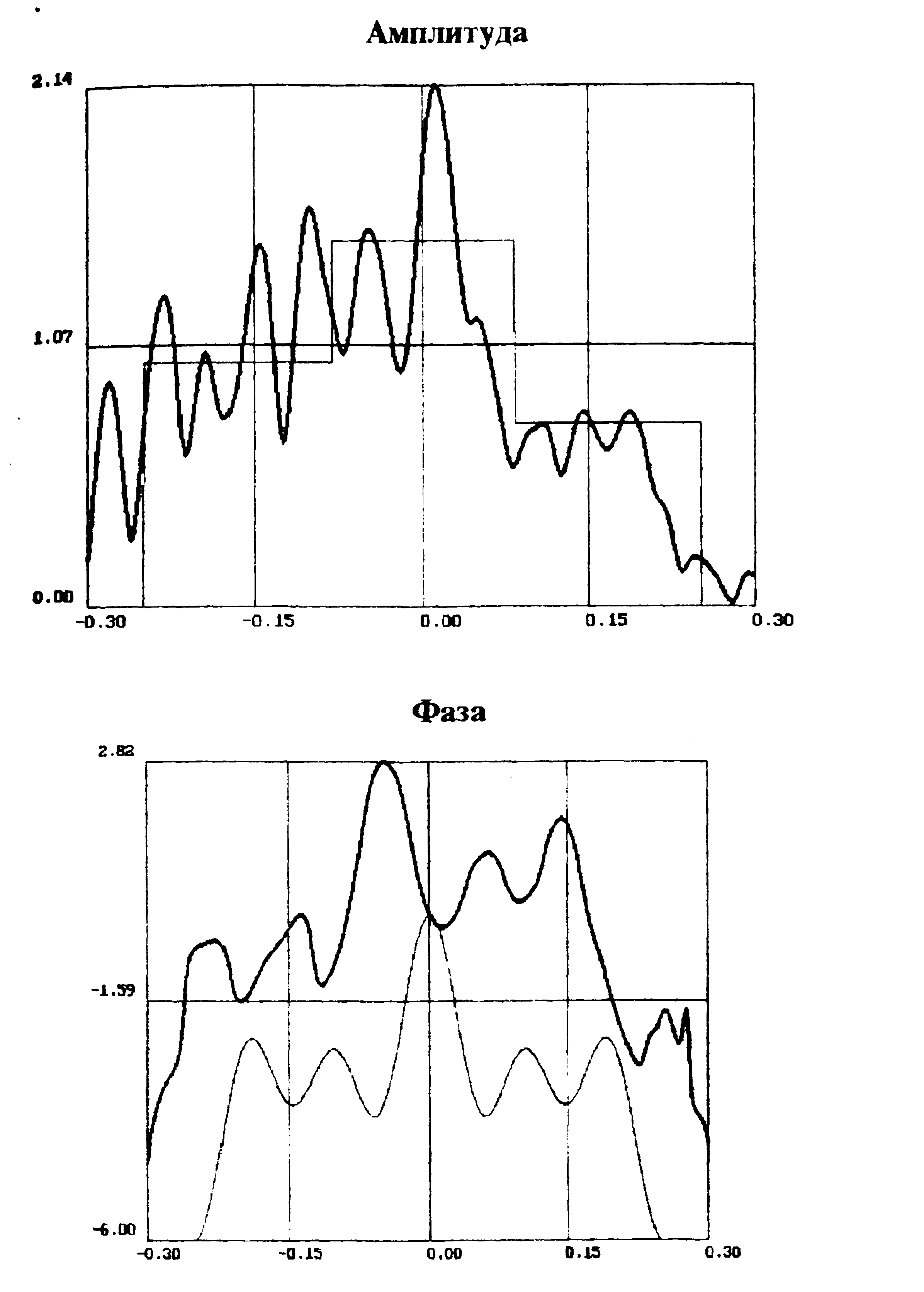
Рис.2. Исходное и восстановленное объектное поле при l = 80 мм. и Dl=2.5 мм., отношение сигнал-шум = 100
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

