В.В.ИВАХНИК, В.И.НИКОНОВ
ТОЧНОСТЬ ОБРАЩЕНИЯ ВОЛНОВОГО ФРОНТА ПРИ ЧЕТЫРЕХВОЛНОВОМ ВЗАИМОДЕЙСТВИИ НА ТЕПЛОВОЙ НЕЛИНЕЙНОСТИ
Среды с тепловым механизмом нелинейности привлекают исследователей прежде всего возможностью использования их для обращения волнового фронта (ОВФ) излучения среднего ИК диапазона длин волн [1,2]. Один из основных вопросов, решаемых при практическом использовании четырехволновых преобразователей излучения, обращающих волновой фронт, на любом типе нелинейности - точность обращения волнового фронта, т.е. насколько комплексная амплитуда отраженной волны А4 соответствует комплексной амплитуде падающей волны А3. В общем виде задача о четырехволновом взаимодействии является типично нелинейной задачей, решение которой не позволяет ввести некоторую функцию (или несколько функций), не зависящую от характеристик падающей волны и устанавливающую однозначную связь между комплексными амплитудами А4 и А3*. Однако в приближении заданного поля по накачкам ( А1 и А2 - комплексные амплитуды волн накачки) система уравнений, описывающая четырехволновое взаимодействие на большинстве типов нелинейности, в том числе и на тепловой нелинейности, линеаризируется относительно комплексных амплитуд падающей и отраженной волн. Поэтому точность ОВФ при таком приближении можно полностью описать с помощью функции размытия точки (ФРТ) [3,4].
В настоящей работе анализируется вид ФРТ вырожденного четырехволнового преобразователя излучения на тепловой нелинейности в схеме со встречными волнами накачки.
Скалярное волновое уравнение, описывающее стационарное четырехволновое взаимодействие в среде с теадловой нелинейностью, имеет вид
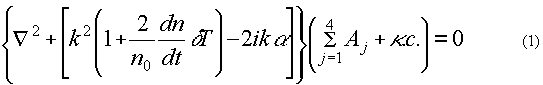
Здесь n0 - среднее значение показателя преломления, k - волновое число, α - коэффициент поглощения, δТ - изменение температуры, обусловленное выделением тепла при поглощении излучения веществом. При записи уравнения (1) считали, что при поглощении излучения изменением показателя преломления вследствии изменения плотности среды можно пренебречь. Уравнение (1) необходимо дополнить уравнением Пуассона, описывающим пространственное изменение температуры,
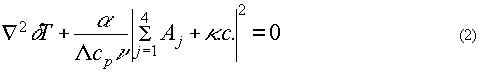
где Λ - коэффициент теплопроводности, cр - удельная теплоемкость, ν- объемная плотность вещества. Наряду с упомянутым выше при анализе уравнений (1-2) будем использовать еще ряд ограничений:
1) четырехволновое взаимодействие рассматривается при квази-колдинеарной геометрии в неограниченном плоском слое, расположенном перпендикулярно оси Z между плоскостями z=0 и z=l,
2) водны накачки являются плоскими:
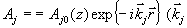 - волновой вектор j-й волны,
- волновой вектор j-й волны,
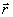 - радиус вектор, j=1,2 ) и распространяются навстречу друг другу
- радиус вектор, j=1,2 ) и распространяются навстречу друг другу
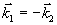
3) тепловая решетка записывается в среде первой волной накачки и падающей волной;
4) коэффициент отражения четырехволнового преобразователя
излучения мал ( |A3|>>|A4|);
5) при расчетах применяется параксиальное приближение.
Изменение температуры, обусловленное выделением в среде тепла, представим в виде суммы быстро и медленно осциллирующих в пространстве составляющих: 
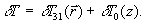 Причем быстро осциллирующую в пространстве составляющую изменения
Причем быстро осциллирующую в пространстве составляющую изменения
температуры разложим по гармоническим решеткам
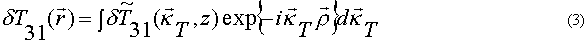
Здесь 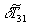 -амплитуда спектра тепловой решетки;
-амплитуда спектра тепловой решетки; 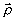 -поперечная составляющая радиус-вектора,
-поперечная составляющая радиус-вектора, 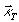 , -вектор гармонической решетки.
, -вектор гармонической решетки.
Падающую и отраженную волны разложим по плоским волнам
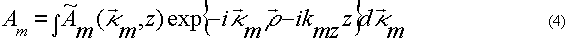
Здесь 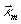 и kmz- поперечная и продольная составляющие волнового вектора
и kmz- поперечная и продольная составляющие волнового вектора 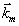 , m=3,4,
, m=3,4, 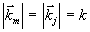 .
.
Используя уравнения (1-2) и выражения (3-4), легко получить выражение для амплитуды спектра тепловой решетки
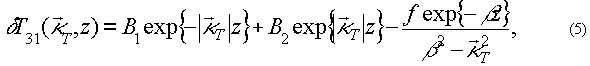
где 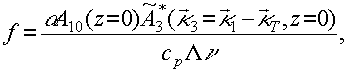
 , - поперечная составляющая векто-
, - поперечная составляющая векто-
pa 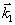 , задающая направление распространения волн накачки.
, задающая направление распространения волн накачки.
Для определения постоянных В1 и В2 предположим, что тепловая решетка записывается при условии отвода тепла от обеих граней нелинейной среды 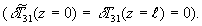 В этом случае выражение для
В этом случае выражение для 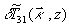 может быть записано в виде
может быть записано в виде
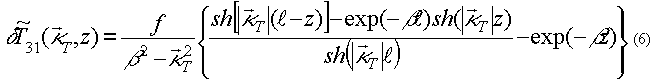
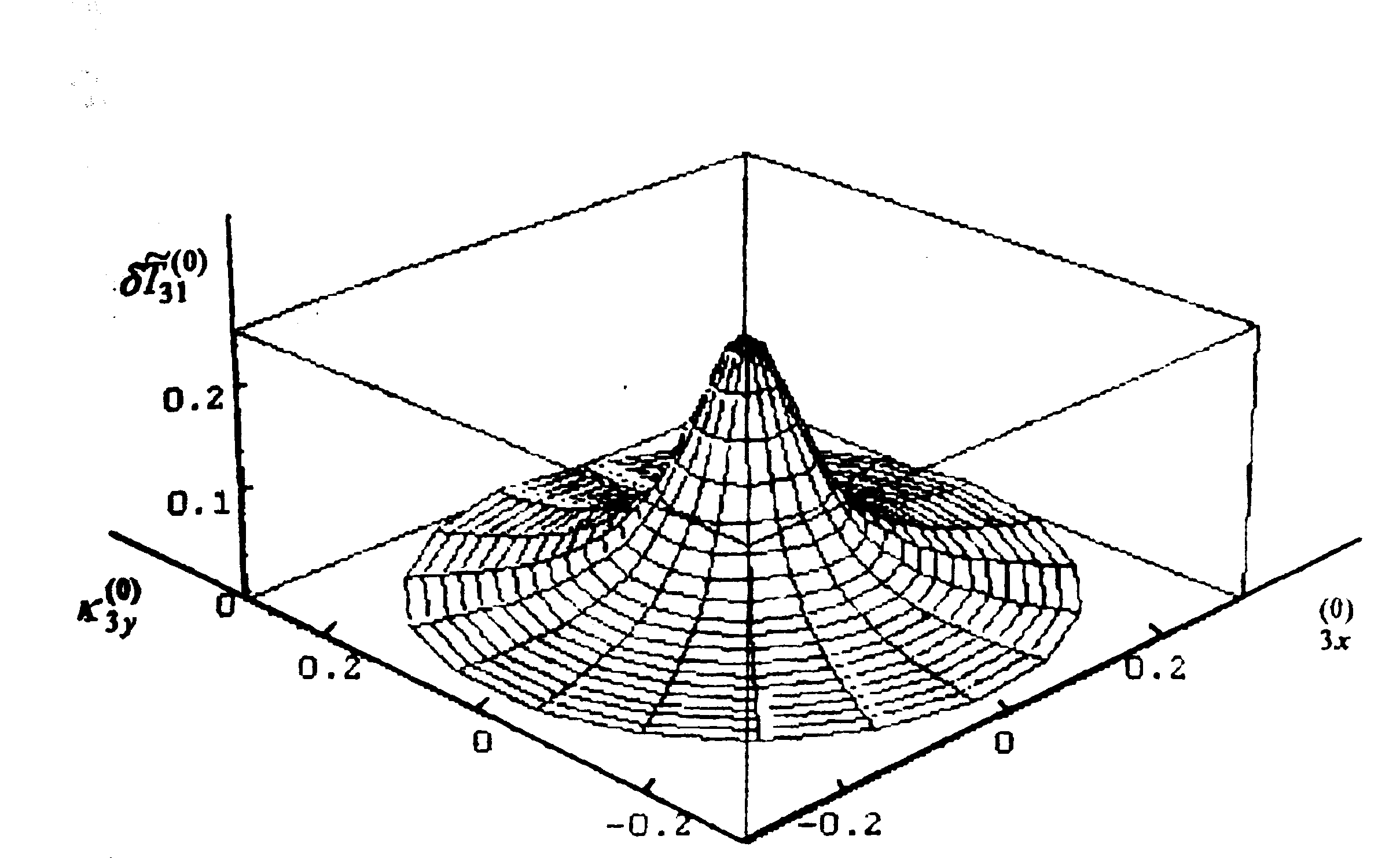
Рис. 1. График модуля амплитуды спектра тепловой решетки при
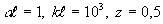
На рис. 1 приведен характерный график нормированной зависимости модуля амплитуды спектра тепловой решетки 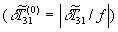 от нормированной поперечной составляющей волнового вектора падающей волны
от нормированной поперечной составляющей волнового вектора падающей волны 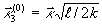 в фиксированной плоскости нелинейной среды. При коллинеарном распространении волн накачки максимальное значение модуля функции
в фиксированной плоскости нелинейной среды. При коллинеарном распространении волн накачки максимальное значение модуля функции 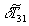 наблюдается при
наблюдается при 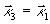 . С ростом величины
. С ростом величины 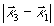 модуль функции
модуль функции 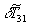 монотонно уменьшается. Если график функции
монотонно уменьшается. Если график функции 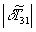 рассечь плоскостью, параллельной плоскости
рассечь плоскостью, параллельной плоскости 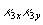 и отстоящей от нее на расстоянии
и отстоящей от нее на расстоянии 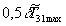 (
( 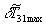 - наибольшее значение модуля амплитуды спектра тепловой решетки в плоскости Z), получится окружность, диаметр которой определяет ширину пространственного спектра амплитуды падающей волны (
- наибольшее значение модуля амплитуды спектра тепловой решетки в плоскости Z), получится окружность, диаметр которой определяет ширину пространственного спектра амплитуды падающей волны (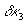 ) в
) в
плоскости Z, в пределах которого наблюдается эффективная з-d-пись тепловых решеток. Величина 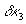 слабо меняется с изменением коэффициента поглощения нелинейной среды, направлением распространения волн накачки. По мере удаления от передней грани нелинейной среды наблюдается небольшое уменьшение величины
слабо меняется с изменением коэффициента поглощения нелинейной среды, направлением распространения волн накачки. По мере удаления от передней грани нелинейной среды наблюдается небольшое уменьшение величины  .
.
Анализ амплитуды спектра тепловой решетки позволяет качественно судить о точности ОВФ.
Для нахождения ФРТ четырехволнового преобразователя излучения на тепловой нелинейности, вновь используя (1-2), запишем укороченное уравнение для амплитуды пространственного спектра отраженной волны
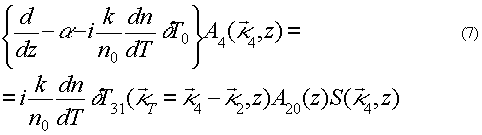
где 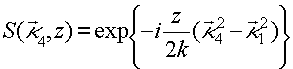 . Заметим, что если ОВФ рассматривать при четырехволновом взаимодействии в схеме с попутными волнами накачки, то в выражении (7)
. Заметим, что если ОВФ рассматривать при четырехволновом взаимодействии в схеме с попутными волнами накачки, то в выражении (7) 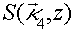 нужно заменить на
нужно заменить на 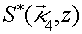 .
.
В приближении плоских волн накачки наличие в уравнении (7) составляющей поля температуры δT0(z) приводит к возникновению в отраженной волне фазовой добавки, величина которой не зависит от поперечной координаты. Поэтому с точностью до постоянного множителя учет δT0(z) не влияет на качество ОВФ.
Падающую волну зададим в виде точки в плоскости, расположенной на расстоянии z1 от передней грани нелинейного слоя. Тогда на передней грани нелинейного слоя амплитуда пространственного спектра падающей волны есть
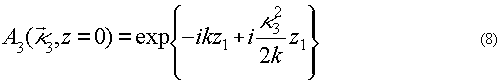
Отраженную волну будем рассматривать в плоскости, отстоящей от передней грани нелинейного слоя на расстоянии z2.
Решая уравнение (1) с учетом (8) и граничным условием 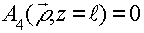 , получим с точностью до постоянного множителя выражение для ФРТ вырожденного четырехволнового преобразователя излучения на тепловой нелинейности вида
, получим с точностью до постоянного множителя выражение для ФРТ вырожденного четырехволнового преобразователя излучения на тепловой нелинейности вида
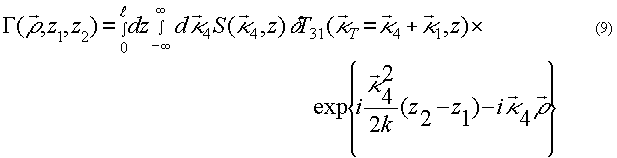
При z1=z2 исчезает зависимость ФРТ от положения плоскости, в которой задается падающая волна 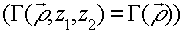 .
.
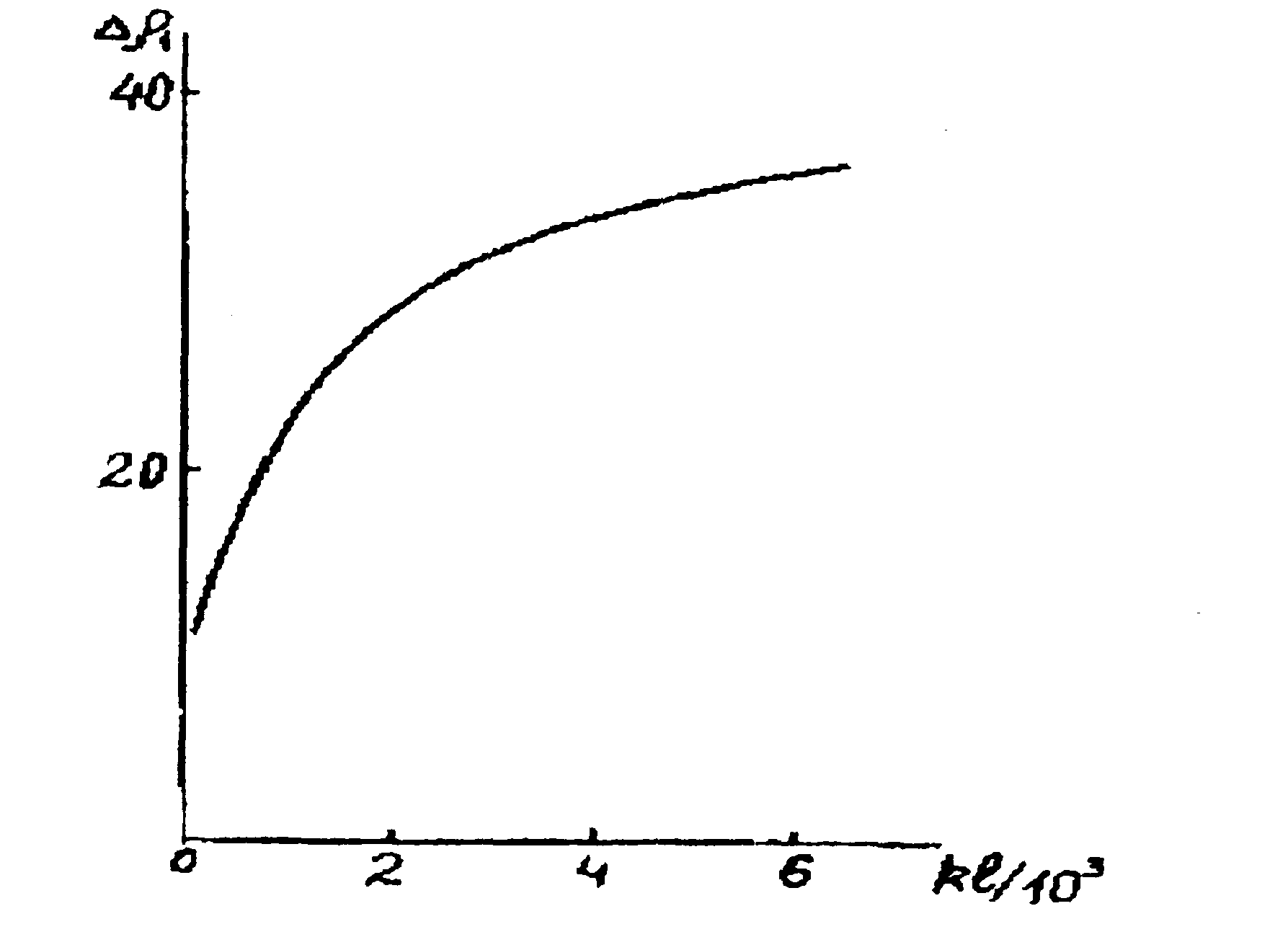
Рис.2. График нормированной ширины модуля ФРТ при к1 =0, α/k=10-3
Численный анализ выражения (9) показывает, что с ростом поперечной координаты 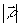 модуль ФРТ монотонно уменьшается.
модуль ФРТ монотонно уменьшается.
В оптике для характеристики преобразования изображения линейной оптической системой вводятся понятие разрешающей способности, определяемой шириной модуля ФРТ. На рис. 2 приведен характерный график зависимости нормированной ширины модуля ФРТ 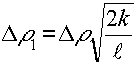 (ширина модуля ФРТ определяется из уравнения
(ширина модуля ФРТ определяется из уравнения 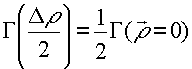 )от толщины нелинейной среды. При небольшой толщине нелинейной среды нормированная ширина модуля ФРТ увеличивается с ростом параметра
)от толщины нелинейной среды. При небольшой толщине нелинейной среды нормированная ширина модуля ФРТ увеличивается с ростом параметра 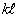 , по закону, близкому к линейному, то есть
, по закону, близкому к линейному, то есть 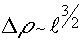 . Дальнейшее увеличение толщины нелинейной среды приводит к выходу кривой зависимости Δρ1 от параметра
. Дальнейшее увеличение толщины нелинейной среды приводит к выходу кривой зависимости Δρ1 от параметра 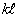 . на постоянный уровень. Величина этого уровня уменьшается с увеличением отношения коэффициента поглощения к волновому числу.
. на постоянный уровень. Величина этого уровня уменьшается с увеличением отношения коэффициента поглощения к волновому числу.
Таблица 1
|
Материал |
n |
α
(см-1) |
Δρ (μм) |
|
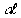 =0,3 =0,3
|
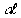 =1 =1
|
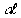 =3 =3
|
|
Si |
3,41 |
2,5 |
0,62 |
1,82 |
4,88 |
|
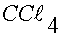
|
1,46 |
18 |
0,078 |
0,26 |
0,7 |
|
CS2 |
1,6 |
1 |
1,38 |
4,62 |
11,98 |
|
Ацетон |
1,35 |
25 |
0,055 |
0,18 |
0,5 |
В таблице 1 приведены результаты расчетов ширины ФРТ для сред, наиболее часто используемых для обращения волнового фронта при четырехволновом взаимодействии на тепловой нелинейности. Значения показателя преломления n и коэффициента поглощения α в таблице1 приведены ддя длины волны 10,6 мкм [5] К сожалению, авторам неизвестны экспериментальные работы по преобразованию изображения при вырожденном четырехволновом взаимодействии на тепловой нелинейности, что не позволяет про-
вести количественное сравнение полученных в работе результатов с экспериментом. Качественное сравнение теоретических и экспериментальных результатов можно провести, проанализировав точность компенсации фазовых искажений в оптической системе, содержащей обращающий волновой фронт четырехволновой преобразователь излучения. Компенсация искажений в таких системах возможна лишь при условии, что характерный размер неоднородностей искажающей среды будет не меньше ширины ФРТ четырехволнового преобразователя излучения [3]. Таким образом, знание минимального размера неоднородностей искажающей среды, при котором еще наблюдается компенсация фазовых искажений в упомянутых выше оптических системах, может быть использована ддя определения разрешающей способности четырехволнового преобразователя излучения. Оценки минимального размера неоднородностей искажающей среды, взятые из экспериментальной работы [6], совпадают с шириной ФРТ четырехволнового преобразователя излучения, рассчитанной с использованием выражения (9) с учетом характеристик среды с тепловой нелинейностью, на которой в работе [6] осуществлялась запись тепловой решетки.
Литература
1. Антипов О.Л., Бетин А.А., Жуков Е.А., Тургенев С.Г.// Препринт №193. Институт прикладной физики АН СССР. Горький, 1988.
2. Васильев Л.А., Галушкин М.Г., Сереган А.М., Чебуркин Н.В. // Квантовая электроника. 1982. Т.9. № 8. С.1571-1575.
3. Воронин Э.С., Ивахник В.В., Петникова В.М., Соломатин B.C., Шувалов В.В. // Квантовая электроника. 1979. Т.6. № 9. С. 2004-2009.
4. Ивахник В.В., Никонов В.И. // Оптика и опектороскопия. 1991. Т.71.№5.С.847-851.
5. Басов Н.Г., Ковалев В.И., Файзулов Ф.С. // Изв. АН СССР. Сер. Физическая. 1987. Т.51. № 2. С. 280-288.
6.Бетин А.А., Жуков Е.А., Митропольский О.В. // Квантовая электроника. 1985. Т.12. № 9. С. 1890-1894.

