В.П.РЯБУХО, А.А.ЧАУССКИЙ, И.Ф.ТЕРЕНТЬЕВА
ЛАЗЕРНАЯ ИНТЕРФЕРОМЕТРИЯ СЛУЧАЙНО НЕОДНОРОДНЫХ ОБЪЕКТОВ
Введение
В настоящей работе рассматриваются физические основы нового направления в интерферометрии - лазерной интерферометрии случайно неоднородных объектов, в рамках которого в отличие от классических методов в качестве измерительного сигнала не форма интерференционных полос или динамика их изменения, а контраст полос, несущий информацию о статистических параметрах объекта.
При отражении когерентного лазерного излучения от объектов с малой степенью шероховатости формируются так называемые частично развитые спекл-поля [1-3], статистические параметры которых занимают промежуточные значения между характеристиками невозмущенного когерентного поля с гладким волновым фронтом и характеристиками развитого спекл-поля. При интерференции лазерных полей, не возмущенных рассеивающим объектом, формируется интерференционная картина с максимальным контрастом, равным единице при равенстве интенсивностей полей. Интерференция гладкой волны с частично развитым спекл-полем приводит к уменьшению контраста полос, значение которого может служить мерой параметров неоднород-ностей объекта, например, степени шероховатости или дефектности поверхности.
Задача установления связи контраста интерференционных полос, наблюдаемых в рассеянном поле, с параметрами рассеивающего объекта (в частности, степенью шероховатости поверхности) и разработки на этой основе соответствующих методов измерения ставилось неоднократно [4-7]. Однако эта важная для практики задача до сих пор не решена, что объясняется, на наш взгляд, недостаточностью разработки основных теоре-
тических и экспериментальных положений интерференции когерентных, но претерпевших диффузное рассеяние оптических полей, а также неоправданностью прямого переноса классической теории когерентности квази-монохроматического теплового излучения протяженных источников света [8] для описания явления интерференции в диффузно-когерентном свете.
В настоящее время по отношению к когерентным диффузно рассеянным световьм полям применяют термин "оптические спекл-поля". Различают поля с развитой и частично развитой спекл-структурами. Теоретические основы интерференции развитых спекл-полей применительно к задачам голографической интерферометрии разработаны в [9-15], а также в [1б]. В более широкой постановке вопроса основные положения интерференции развитых спекл-полей в классических интерферометрах, в голографической интерферометрии и спекл-фотографии, а также с использованием многомодовых оптических волокон рассмотрены в работах [17-20]. Развитые спекл-поля формируются сильными рассеивателями с δ-коррелированным граничным полем и характеризуются единичным контрастом пространственных флуктуации интенсивности и кoppeляциoнными свойствами, определяемыми в соответствии с аналогом теоремы Ван-Циттерта-Цернике [21-24]. При интерференции таких полей полосы средней интенсивности (осредненной по ансамблю реализации спекл-полей или по площади, значительно превышающей размеры спеклов) формируются только при суперпозиции идентичных спекл-полей и имеют локализованный характер. Для неидентичных спекл-полей, образованных различными рассеивателями, или для идентичных, но полностью де-коррелированных из-за их взаимного сдвига, пространственное перераспределение интенсивности наблюдается или в отдельных спеклах - регулярные полосы формируются внутри спеклов, или между соседними спеклами, когда ширина полос превышает размеры спеклов. Иначе проявляется интерференция частично развитых спекл-полей, имеющих неединичный контраст флуктуации интенсивности [1,2]. Важной особенностью этих полей является наличие в них нерассеянной (зеркальной, направленной) составляющей [1,2,22], интенсивность которой определяется статистическими свойствами рассеивающего объекта (см. также [25,26]). Контраст спеклов и автокорреляционная функция комплексной амплитуды частично развитых спекл-полей также несут информацию о статистических свойствах неоднородностей
объекта [22,24,27-29]. При интерференции таких полей с когерентной гладкой опорной волной или другим частично развитым спекл-полем формируются интерференционные полосы средней интенсивности, контраст которых определяется степенью взаимной корреляции интерферирующих полей и статистическими характеристиками рассеивателя. В [30,31] рассмотрена интерференция частично развитого спекл-поля с гладкой волной и показана зависимость между относительным значением минимальной интенсивности в интерференционной картине при условии противофазности и полной согласованности интерферирующих полей, с одной стороны, и статистическими моментами амплитуды и фазы рассеянного поля, с другой. Однако более важной характеристикой и с практической (измерительной), и с методологической точек зрения является контраст наблюдаемых интерференционных полос, его зависимость от статистических параметров рассеивателей - источников спекл-полей.
В работах [32-37] получены теоретические и экспериментальные результаты, определяющие зависимость контраста интерференционных картин, наблюдаемых при суперпозиции частично развитых спекл-полей, от статистических характеристик определенного класса рассеивающих объектов. Эти результаты можно рассматривать в качестве теоретико-экспериментального задела на пути разработки физических основ методов и средств лазерной интерферометрии случайно неоднородных объектов, в частности, степени шероховатости изделий прецизионного машиностроения, точного приборостроения, электронной техники, а также объектов биомедицины.
Теоретические результаты
В [32] исследованы закономерности интерференции частично развитых спекл-полей, формирующихся при рассеянии лазерного излучения на объектах, оказывающих достаточно слабую модуляцию освещающего поля. С практической точки зрения именно такие объекты представляют наибольший интерес в задачах контроля неоднородностей. В качестве физической модели в [32] рассмотрен случайный фазовый экран (СФЭ) [24,38] - объект с достаточно плавными фазовыми неоднородно-стями различной природы. В предположении гауссовой статистики этих неоднородностей установлены зависимости контраста
полос от дисперсии фазовых флуктуации σф2, приобретаемых
освещающим полем при его взаимодействии с объектом. Дисперсия σ2 напрямую связана с дисперсией неоднородностей объекта. Например, для отражающего объекта со случайным микрорельефом поверхности σф2 = (4πσh/λ) 2 , где σh2 - дисперсия высот неровностей, при нормальном падении освещающего лазерного пучка. Для пропускающего объекта - σф2 = [2π(n-n0)σh /λ]2 , где n и n - показатели преломления объекта и окружающей среды соответственно. В [32] показано, что однозначная связь контраста полос V и σф2 выполняется для граничного поля и ближней области пространства, непосредственно примыкающей к поверхности объекта, где корреляционные характеристики рассеянного поля, а значит, и средней интенсивности не претерпевают существенного изменения [38,28-31]. Исходя из этого положения, соответствующим образом должны строиться схемы лазерных интерферометров, предназначенных для измерения параметров неоднородностей по контрасту полос средней интенсивности.
В практике интерференции спекл-полей необходимо выделить два принципиально отличающихся случая - интерференция идентичных (коррелированных) и неидентичных (некоррелированных) спекл-полей, для реализации которых должны использоваться различные схемные решения и методы. В частности, для реализации интерференции идентичных спекл-полей эффективен метод голографической интерферометрии, неидентичных - методы классической интерферометрии.
Для средней интенсивности картины интерференции спекл-полей можем записать выражение [17]
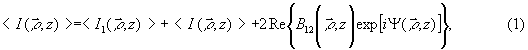
где B12(ρ,z) - взаимная корреляционная функция комплексных амплитуд интерферирующих полей; Ψ (ρ, z) - δетерминированная разность фаз. Для частично развитых спекл-полей имеем [32]
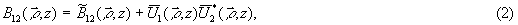
где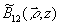 
- взаимная корреляционная функция флуктуацион-ных компонент полей; 
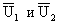-комплексные амплитуды средних
(нерассеянных) составляющих полей, для которых в области граничного поля (z = 0) при гауссовой статистике СФЭ справедливо выражение
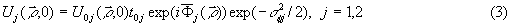
где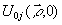 
- комплексная амплитуда поля, освещающего СФЭ с
коэффициентом пропускания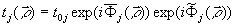 
,
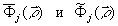- средняя и флуктуационная составляющие фазового набега; σφj2 - дисперсия фазовых флуктуации. При интерференции идентичных спекл-полей, но декоррелированных из-за их взаимного пространственного сдвига
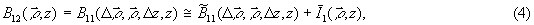
где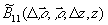 
- автокорреляционная функция флуктуацион-ной составляющей спекл-поля, 
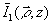- интенсивность нерассеянного компонента. В (4) было учтено, что для идентичных спекл-
полей σφ12=σφ22, t01=t02 , b использованы приближения
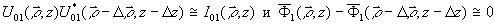в силу предполагаемой медленной зависимости U0 и 
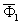от координат 
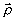, и равенства интенсивностей освещающих волн. Если между полями создан взаимный сдвиг 
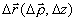превышающий радиус корреляции поля 
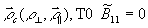и для контраста полос получаем выражение
Для граничного поля или области постоянства средней интенсивности рассеянного поля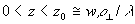 
где w -
радиус освещающего пучка [38],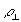 
- поперечный радиус корреляции флуктуационного компонента граничного поля, контраст полос средней интенсивности определяется выражением
При удалении плоскости наблюдения от объекта, при z >>z0 средняя интенсивность флуктуационного компонента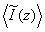 
умень-
шается быстрее, чем интенсивность среднего поля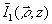 
, и поэтому средняя интенсивность полного поля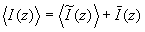 
стремится к интенсивности нерассеянного компонента, а контраст полос Vs, как это следует из формулы (5), стремится к единице Vs→1.
При интерференции двух неидентичных частично развитых спекл-полей (одно поле может быть "гладким") взаимная корреляционная функция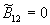 
и корреляция полей проявляется только через нерассеянные компоненты, 
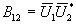. Тогда, если I01=I02, то для контраста полос средней интенсивности в ближней области получаем
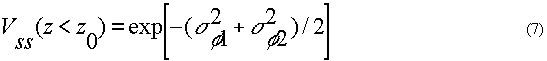
При удалении от рассеивающего объекта контраст полос увеличивается и стремится к предельному значению в дальней области дифракции
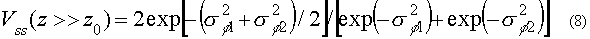
Нетрудно получить выражение для контраста полос, когда опорная волна имеет гладкий волновой фронт,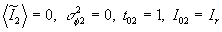 
. Если 
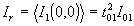, то для z<zo контраст определяется выражением
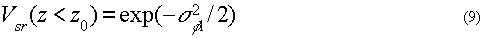
Если интенсивности опорного и объектного полей равны в дальней зоне дифракции, то контраст полос в области граничного поля определяется уже другим выражением
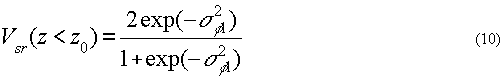
Уравнения (6) - (10), по которым просто определить значения σφ2, а значит, и соответствующие значения неоднородностей объекта, могут быть положены в основу метода измерения параметров неоднородаостей объекта при соответствующем схемном решении для интерферометра. Однако в этих уравнениях отсут-
ствуют другие важные статистические параметры объекта, такие как радиус корреляции неоднородностей 1φ и средняя форма этих неоднородностей, совпадающая с формой коэффициента корреляции пространственных флуктуации фазы граничного поля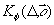 
. В практических технологических проблемах эти параметры могут иметь важное значение и им уделяется повышенное внимание (см., например, [39,40]). Вместе с этим, соотношения (6) -(10) получены, что оговаривалось выше, в предположении гауссовой статистики неоднородностей, что далеко не всегда имеет место для реальных объектов.
Радиус корреляции неоднородностей и их средняя форма проявляются в динамике изменения контраста полос при удалении от объекта. Отчетливое проявление формы коэффициента корреляции фазы неоднородностей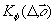 
, как показано в [34-37], наблюдается в форме кривой изменения контраста полос средней интенсивности в продольном направлении, при освещении СФЭ пространственно-модулированньм лазерным пучком.
Выше предполагалось, что для наблюдения интерференции идентичных спекл-полей используются схемы интерферометров по классической терминологии с делением волн по амплитуде [8]. Возможно эффективное применение и схемы с делением по волновому фронту, например, схемы Юнга. Однако в варианте использования экрана с малыми отверстиями, как, например, в [41,42], такая схема приемлема для исследовательских целей и совершенно неэффективна в практическом применении из-за больших энергетических потерь. В работе [33] показано, что схема Юнга может быть модифицирована при использовании двух сфокусированных на контролируемой поверхности лазерных пучков. Применялся лазерный пучок с пространственной модуляцией в виде прямолинейных интерференционных полос, который в области фокусировки распадался на два пятна. При этом в рассеянном излучении реализуется интерференция неидеятичных частично развитых спекл-полей, которые при неподвижном объекте не формируют полос средней интенсивности. В зависимости от соотношения размеров спеклов ε┴ и периода ожидаемых полос Λ
интерференционные полосы могут наблюдаться при ε┴ >Λ θли не наблюдаться вовсе, если ε┴ < Λ (β последнем случае имеет место частичное перекрытие освещающих пучков на поверхности объек-
та). Однако если привести в движение рассеиватель, то происходит смена реализации спекл-полей, что позволяет провести осреднение спекл-полей и наблюдать полосы средней интенсивности, контраст которых определяется параметрами неоднородностей объекта σφ2, 1φ и Кφ. В [33,34,37] показано, что если расходимость нерассеянного (фактически освещающего) лазерного пучка и расходимость флуктуационного (рассеянного) компонента поля тем или иным способом приблизительно уравниваются, то для оценки контраста полос можно использовать уравнение (7) при равенстве σφ12=σφ22, поскольку оба интерферирующих поля образованы одним и тем же объектом. Однако полного равенства расходимостей полей получить не удается, поэтому необходимо учитывать влияние и σφ2 и 1φ . Такие теоретические
расчеты для схемы Юнга со сфокусированными пучками выполнены в [37] при использовании следующих предположений: объект удовлетворяет модели "случайный фазовый экран", статистика неоднородностей - нормальная, форма коэффициента корреляции неоднородностей Кφ - гауссова, освещающий лазерный
пучок имеет гауссов профиль амплитуды. Для этого случая удалось получить в аналитическом виде связь контраста полос средней интенсивности и параметров объекта σφ2 и 1φ для различных сечений поля z
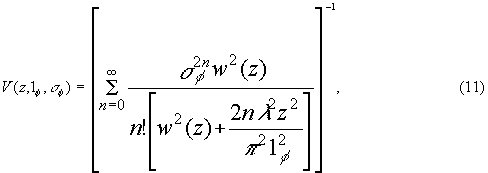
где w(z) - радиус нерассеянного гауссова пучка, z - расстояние от поверхности объекта до плоскости наблюдения. При удалении плоскости наблюдения от объекта контраст полос стремится к стационарному значению, определяемому выражением
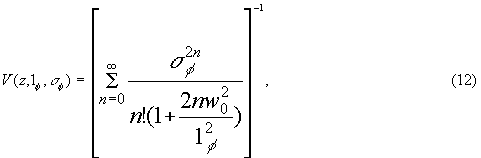
где w0 - радиус перетяжки освещающего гауссова пучка.
Экспериментально установлено, что не требуется точная фокусировка пучка на поверхность, так как при расфокусировке происходит частичное перекрытие пучков на поверхности объекта. В рассеянном поле реализуется интерференция частично идентичных спекл-полей с образованием полос средней интенсивности при неподвижном объекте, контраст которых остается таким же, как и при фокусировке на движущийся объект. Тем самым наглядным образом реализуется эквивалентность двух видов осреднения - по одной реализации и по ансамблю реализации спекл-полей (свойство эргодичности).
Таким образом, в [33,34,37] сделан теоретический и экспериментальный (см. ниже) задел для развития нового и весьма перспективного, по нашему мнению, способа контроля неоднородных объектов, находящихся в движении (например, обрабатываемой в станке детали, турбулентного потока жидкости) с использованием сфокусированного пространственно-модулированного лазерного пучка.
Экспериментальные результаты
В экспериментах объектами исследования служили металлические и диэлектрические образцы с различной степенью шероховатости поверхности, а также фазовые (отбеленные) спекло-граммы, наилучшим образом удовлетворяющие модели "случайный фазовый экран" и позволяющие получать образцы с разнообразными статистическими параметрами путем управления режимом и параметрами схемы записи спеклограмм [32,35]. Использовались как классические схемы интерферометров, так и простые схемные решения [32], позволяющие надежным способом реализовать интерференцию рассеянных когерентных полей. Например, на рис.1 представлена оптическая схема интерферометра, позволяющая наблюдать полосы интерференции идентичных спекл-полей, декоррелированных из-за их взаимного пространственного сдвига, в области, где корреляционные свойства спекл-полей можно считать совпадающими с корреляционными свойствами граничного поля при достаточно широком освещающем лазерном пучке [38,28,29]. Оптический клин в этой схеме служит для формирования полос средней интенсивности и для создания взаимного сдвига интерферирующих спекл- полей, превы-
тающего их радиус корреляции Δr>ρc. В этом случае контраст
полос, период Λ которых существенно превышает поперечный размер спеклов ε┴, определяется выражением (6). Если Λ ≤ε┴ , то
необходимо осреднение по реализациям спекл-полей, что можно выполнить путем поперечного смещения исследуемого объекта.
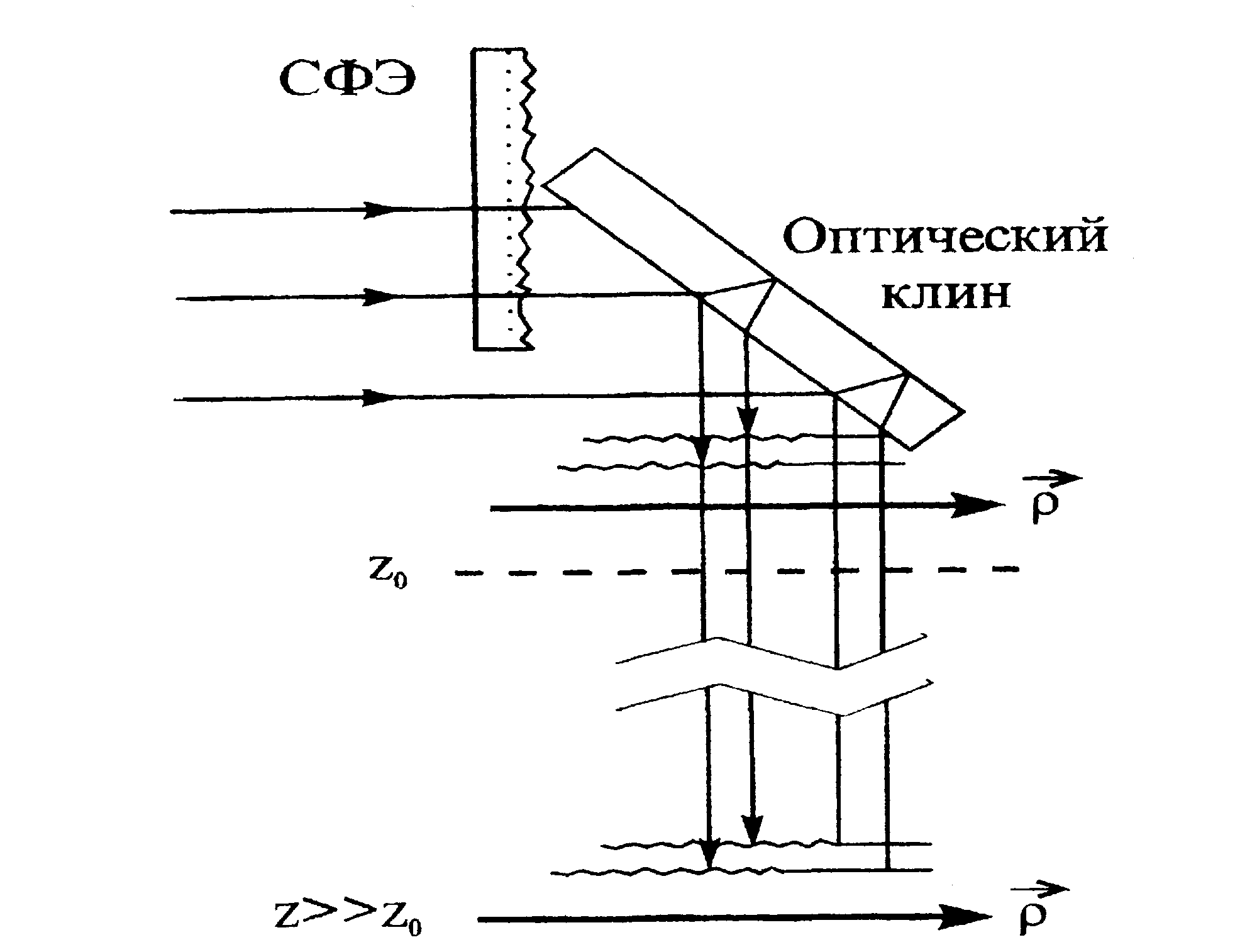
Рис.1. Схема наблюдения интерферограмм идентичных, но декорре-лированных из-за взаимного сдвига частично развитых спекл-полей в ближней и дальней областях дифракции за СФЭ
На рис.2 представлены интерферограммы, полученные с помощью схемы, изображенной на рис.1, с использованием широкого освещающего лазерного пучка и спеклограммы в качестве СФЭ. Верхняя часть интерферограмм имеет почти единичный контраст и образована для сравнения в лазерном пучке, не прошедшем через рассеиватель (рис.1). С удалением от объекта контраст полос средней интенсивности увеличивается и стремится к контрасту интерферограммы сравнения.
Рис.2. Интерферограммы сравнения (верхние части) и полосы интерференции декоррелир о ванных идентичных спекл-полей в ближней (z<z0) и дальней (z>>z0) областях дифракции за СФЭ
Другой метод наблюдения полос средней интенсивности при интерференции идентичных спекл-полей реализуется с помощью освещающего пучка с регулярными интерференционными полосами - пространственно-модулированного лазерного пучка [35,36]. В этом случае в динамике эволюции контраста полос проявляется не только "высотный" параметр σφ , но и поперечные характеристики 1φ, Kφ(Δρ), поскольку взаимный сдвиг спекл-полей Δζ(z) линейно увеличивается с расстоянием z от поверхности объекта, Δζ=λz/Λ. ΐналогичная картина интерференции может быть реализована с помощью голографической интерферометрии путем изменения направления освещения СФЭ на малый угол θ между экспозициями и наблюдения полос в области действительного годографического изображения (рис.З). Для этого необходимо, чтобы все рассеянное излучение попадало на голограмму в область опорного пучка с равномерной интенсивностью. Иначе произойдет фильтрация пространственных частот записанного объектного поля и изменение его корреляционных свойств в области действительного изображения.
Если необходимо определить только σφ , то достаточно между экспозициями сместить объект на величину Δr, заведомо превышающую радиус корреляции поля рд и тем или иным способом создать систему интерференционных полос на голографическом изображении. Эффективным для этих целей может быть вращательный сдвиг объекта в собственной плоскости [16].
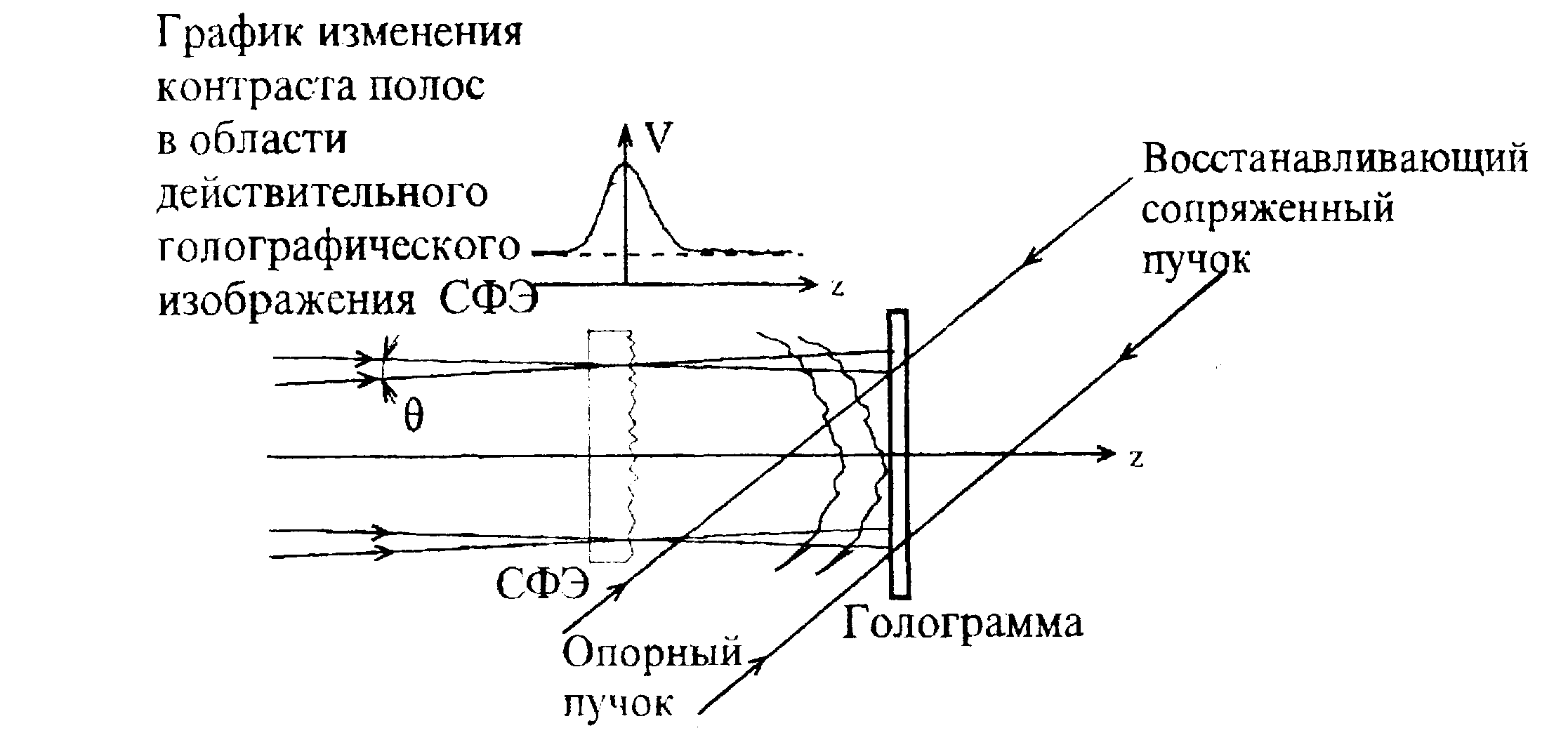
Рис.3. Схема голографической интерферометрии случайно неоднородных объектов
Фазовые спеклограммы на стеклянной подложке представляют очень простую возможность для исследования основных закономерностей интерференции неидентичных спекл-полей или спекл-поля с гладкой опорной волной за счет отражения освещающего пучка от обеих поверхностей спеклограммы [32]. В первом случае одно поле образуется за счет отражения света от неровной поверхности эмульсионного слоя спеклограммы, а второе - за счет двукратного прохождения эмульсионного слоя и отражения от поверхности стеклянной пластины. Во втором случае гладкое опорное поле получается при отражении освещающего пучка от поверхности пластины, а спекл-модулированное поле - за счет двукратного прохождения эмульсионного слоя и внутреннего отражения от его неровной поверхности.
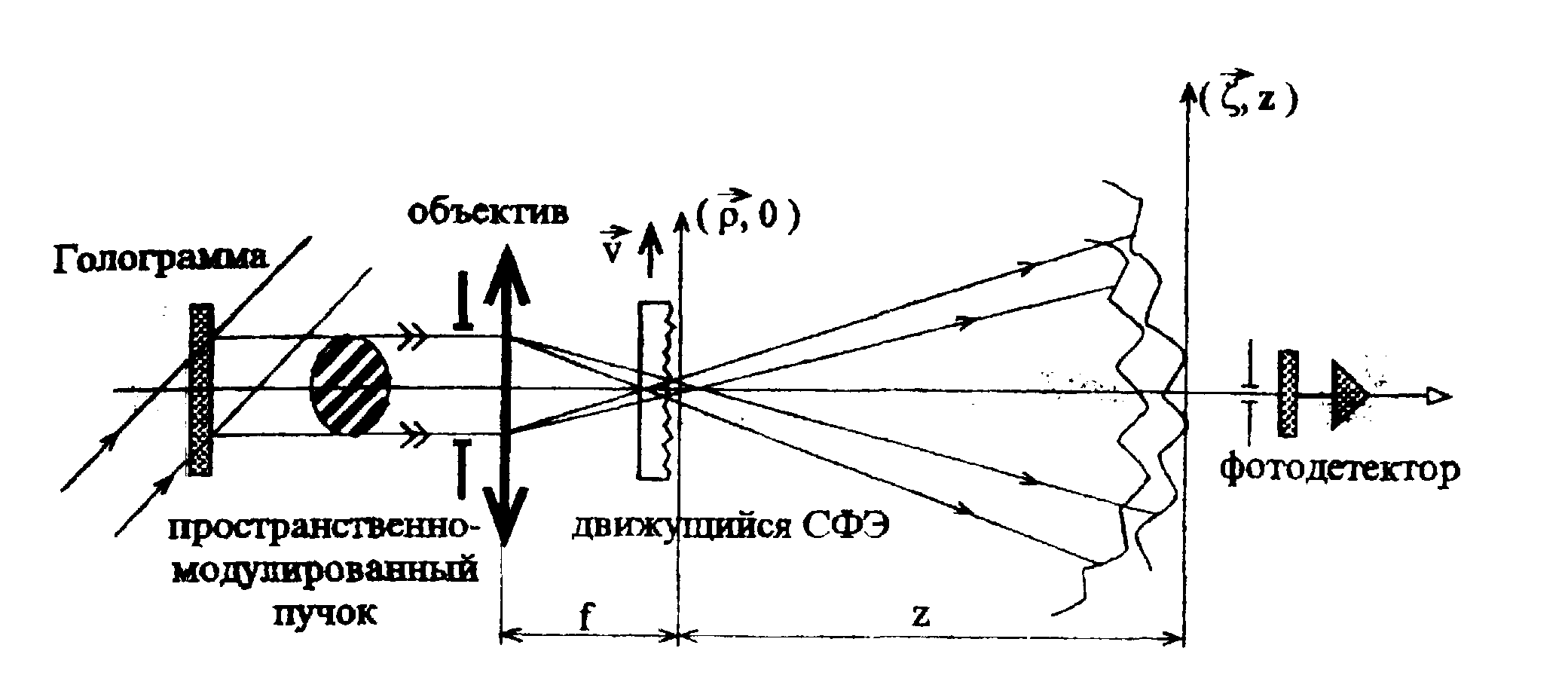
Рис.4. Схема для регистрации интерференционных полос средней интенсивности в зоне дифракции сфокусированного пространственно-модулированного лазерного пучка на движущемся случайном фазовом объекте
Для исследования интерференции спекл-полей, формирующихся при освещении рассеивающего объекта сфокусированными пучками, использовалась оптическая схема, изображенная на рис.4. Лазерный пучок с прямолинейными интерференционными полосами (рис.5,а), получаемый с помощью специального голографического элемента [43], фокусировался объективом приблизительно на поверхность рассеивающего объекта. Если период полос Λ в пучке меньше апертуры дифракционно ограниченного объектива, то в фокальной плоскости формируются два пространственно разделенных (разрешимых) лазерных пятна, которые за счет рассеяния на объекте формируют два неидентичных спекл-поля.
На рис.5,а показан вид интерференционного поля в отсутствии объекта, а на рис.5,6 - при помещении неподвижного объекта в зону фокусировки. Картина полос полностью разрушается, и в наблюдаемом спекл-модулированном поле отсутствуют регулярные полосы. Однако при движении объекта в дифракционном поле с помощью инерционного фотоприемника обнаруживается картина регулярных полос средней интенсивности с контрастом, определяемым параметрами неоднородности объекта (рис.5,в). На рис.6 показаны экспериментальные кривые эволюции контраста полос средней интенсивности при удалении плоскости регистрации от объекта.
Рис.5. Интерферограммы, наблюдаемые в отсутствие (а), при неподвижном (б) и при движущемся (в) случайном фазовом экране
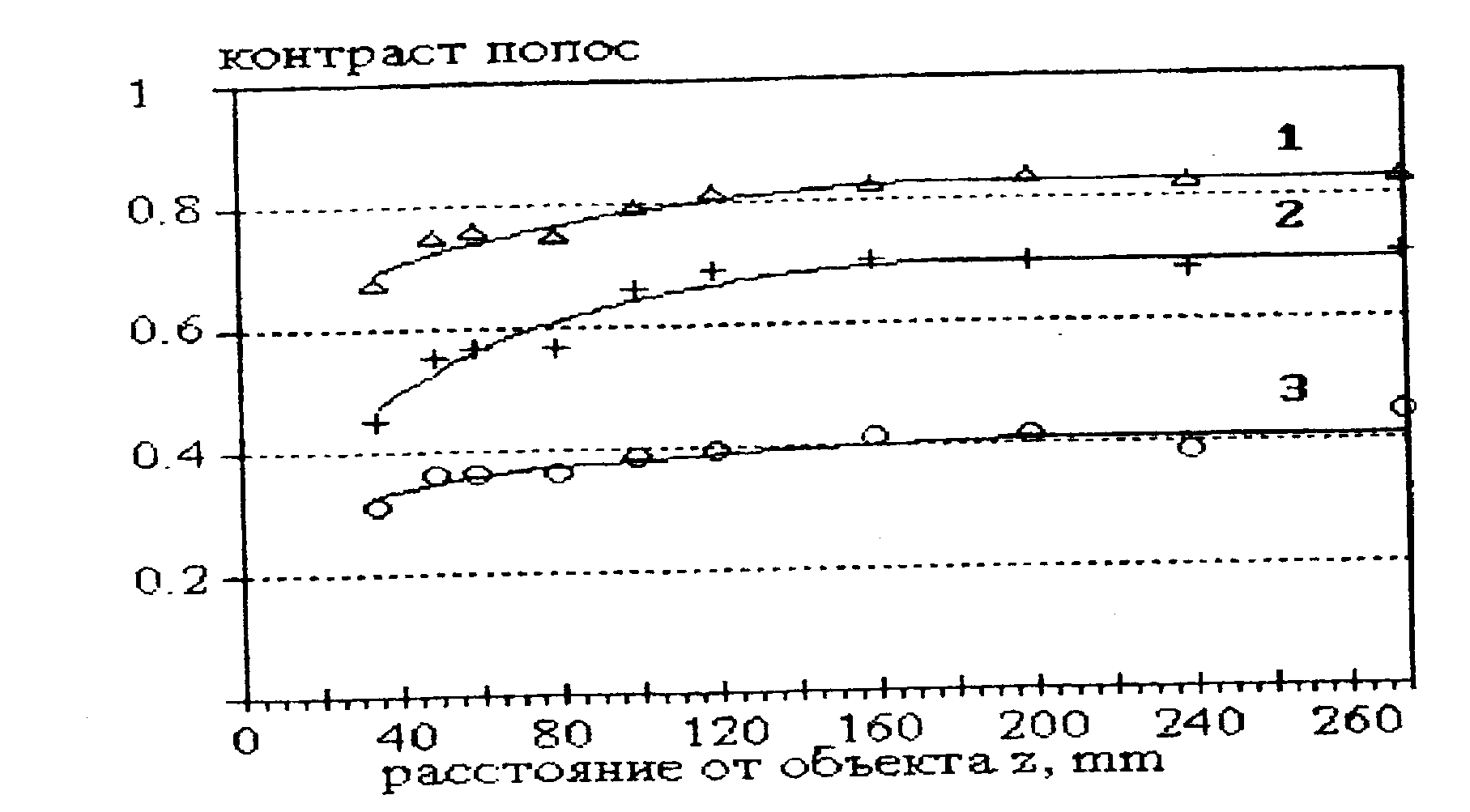
Рис.6. Относительный контраст интерференционных полос средней интенсивности V/V0 в поле дифракции сфокусированного пространственно-модулированного лазерного пучка:
1- σφ1 = 0.7, 1φ1 =11 мкм;
2- σφ2= 1.2, 1φ2 =5 мкм;
3 - σφ3 = 1.2, 1φ3 = 20 мкм
Сопоставление с теоретическими кривыми (рис.7), полученными в результате численных расчетов с помощью выражения (11), показывает достаточно хорошее соответствие. Наблюдаемые различия,
нородностей от нормальной статистики и от принятой в теоретическом анализе гауссовой формы неоднородностей объекта. Более быстрый выход теоретических кривых на стационарный уровень объясняется тем, что в эксперименте поверхность объекта неточно совпадала с перетяжками пучков, а была немного смещена в область расфокусировки.
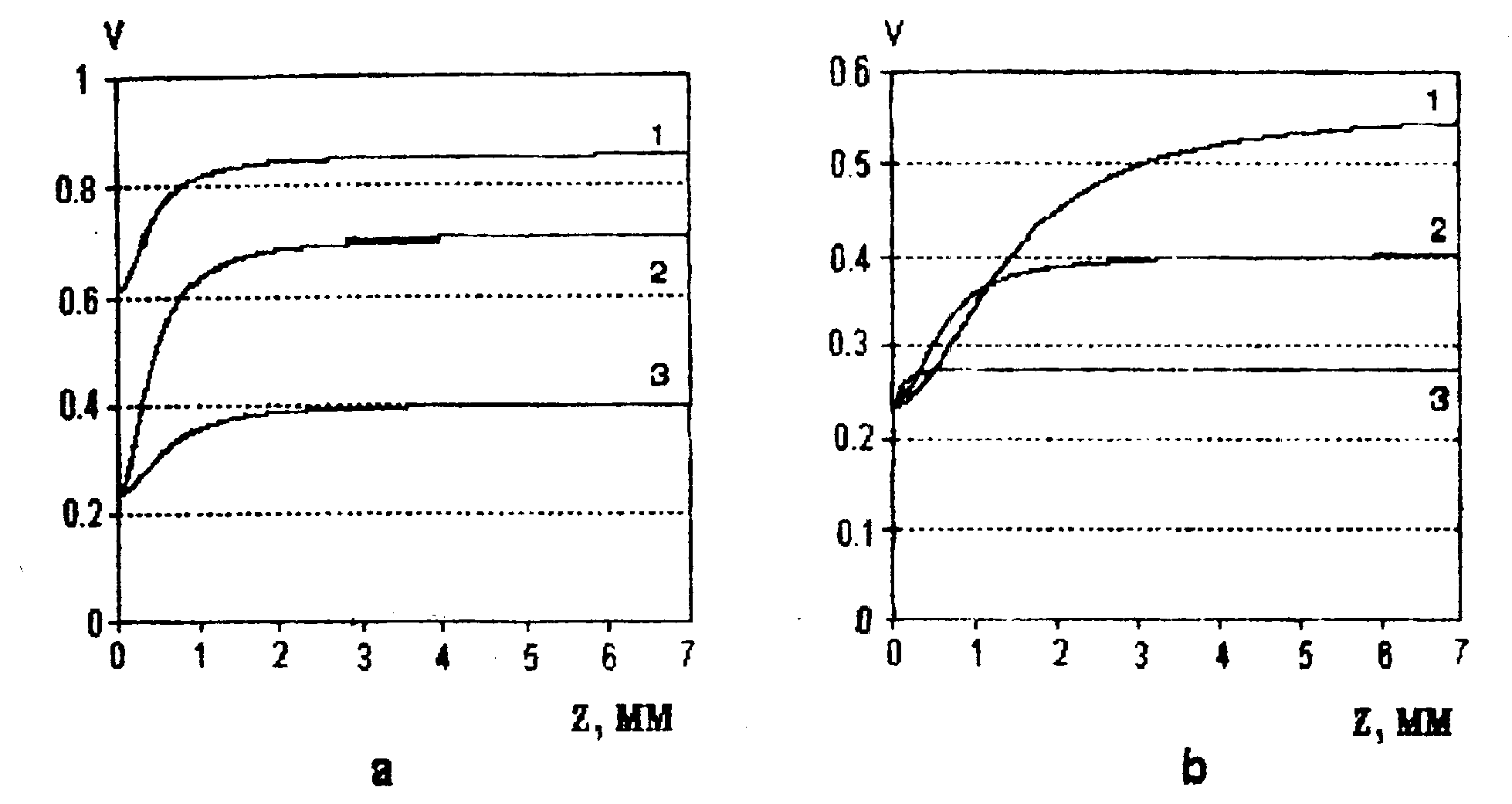
Рис. 7. Контраст интерференционных полос V в зависимости от расстояния г от случайного фазового объекта: а - для различных значений параметров объекта σφ, 1φ (1 - σφ = 0.7, 1φ = 11мкм; 2 - σφ = 1.2, 1φ = 8мкм; 3 - σφ = 1.2, 1φ = 20мкм) с одним и тем же радиусом перетяжки освещающего пучка w0 =72 мкм;
б - для различных значений w0 ( 1 - w0 = 20 мкм; 2 - w0 =12 мкм; 3 -
w0 = 5 мкм) с одними и теми же параметрами объекта σφ = 1.2 и 1φ =20 мкм
Заключение
Теоретические и экспериментальные исследования интерференции лазерных полей с частично развитой спекл-структурой показывают возможность и перспективность (с метрологической точки зрения) разработки методов и средств измерения параметров случайно неоднородных объектов с использованием интерференции света. Измерительная информация в этих методах содержится в контрасте полос средней интенсивности (средней по реализации
или по ансамблю реализации спекл-полей) и в закономерностях его изменения в пространстве вдоль направления распространения световых пучков. Важным для практических применений является разработка схемных решений интерферометров, включая гологра-фические, позволяющих разделять вклад в наблюдаемую картину полос, "высотных" характеристик микронеоднородностей объекта (σφ,σh), их среднего поперечного размера (1φ) и средней формы
Кφ (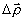
) Полученные результаты в совокупности с результатами работ [28-31] могут рассматриваться в качестве задела в разработке физических основ нового направления в оптической интерферометрии - лазерной интерферометрии случайно неоднородных объектов и сред, направленного на решение ряда важных задач измерений и контроля в прецизионном машиностроении, точном приборостроении, электронной технике, в задачах диагностической биомедицины.
Литература
1. Ohtsubo J. Statistical properties of differentiated partially developed speckle patterns. // JOSA. 1982. V.72. N.9. P.117-120.
2. Grzegorzewski В. Second-order statistics of partially developed
speckle pattern in the far field. // Opt.Acta. 1986. V.33. N.ll. P.1441-
1451.
3. Grzegorzewski В. Contrast of an integrated fringe pattern generated
by partially developed speckle. // Opt. Common. 1988. V.62. N.2. P.117-
120.
4. Городинский Г.М. К вопросу о статистической интерференции при отражении света от матовых стеклянных поверхностей // Опт. и спектр. 1963. Т.15. В.1.C.113-118.
5. Городинский Г.М., Галкина В.Н. К вопросу о нарушении когерентности света матовыми стеклянными поверхностями // ЖПС. 1966. Т.5. В.4. С.451-455.
6. Таганов O.K., Топорец А.С. Исследование степени когерентности излучения, прошедшего шероховатую поверхность // Опт. и спектр. 1976. Т.40. В.4. С.741-746.
7. Топорец А.С. Отражение света шероховатой поверхностью // ОМП. 1979. B.I. C.34-46.
8. Борн M., Вольф Э. Основы оптики /Пер. с англ. M.: Наука, 1973.720с.
9. Walles S. On the concept of homologous rays in holographic interferometry of diffisely reflecting surfaces // Opt.Acta. 1970. V. 17. N.12. P. 899-913.
10. Yamaguchi I. Fringe loci and visibility in holographic interferometry with diffuse objects. 1. Fringes of equal inclination // Opt. Acta. 1977. V.24.N.10.P.1011-1025.
11. Yamaguchi I. Fringe loci and visibility in holographic interferometry with diffuse objects. 2. Fringes of equal thickness // Opt. Acta. 1978. V.25. N.4.P. 299-314.
12. Yamaguchi I. Fringe formations in deformation and vibration measurements using laser light // Progress in Optics, 1985, Vol. 22. ed. E.Wolf. North-Holland, Amsterdam, chap. 5, P. 174-341.
13. Островский Ю.И., Бутусов М.М., Островская Г.В. Голографическаяинтерферометрия. M.: Наука, 1977. 336с.
14. Вест Ч. Голографическая интерферометрия /Пер. с англ. M.. Мир,1982. 504 с.
15. Джоунс Р., Уайкс К. Голографическая спекл-интерферометрия.
/ Пер.с англ. M.: Мир, 1986. 328 с.
16. Клименко И.С., Рябухо В.П., Федулеев Б.В. Проявление тонкой амплитудно-фазовой структуры спекл-полей при их когерентной суперпозиции // ЖТФ. 1985. Т. 55. В 7. С. 1338-1347.
17. Ryabukho V.P., Klimenko I.S., Golubentseva L.I. Interference of laser speckle fields //Proc. SPIE: "New Techniques and Analysis in Optical Measurements". 1994. V. 2340. Р. 513-522.
18. Клименко И.С., Рябухо В.П., Федулеев Б.В. Осцилляция видности и локализация интерференционных полос в спекл-интерферометрии //ЖТФ. 1986. Т. 56. В 9. С. 1749-1756.
19. Клименко И.С., Рябухо В.П., Федулеев Б.В. Локализация интерференционных полос в спекл-интерферометрии // Применение методов и средств голографии. Л.: ЛИЯФ,1989. С. 75-102.
20. Клименко И.С., Рябухо В.П., Федулеев Б.В., Перепелицына О.А. Спекл-интерферометры на многомодовых оптических волокнах и жгутах с совмещенными идентичными спекл-полями // Оптические поля и оптические методы обработки информации. M.: МФТИ, 1991.С.38-44.
21. Власов Н.Г., Пресняков Ю.П. Пространственная корреляция интенсивности в диффузно-когерентном излучении и интерференционные измерения на ее основе // Соврем, проблемы прикладной голографии. M,: МДНТП, 1974. С.13-32.
22. Goodman J.W. Statistical Properties of Laser Speckle Patterns //Laser Speckle and Related Phenomena. Springer- Verlag, Berlin, 1975.P.9-75.
23. Dainty J.C. The statistics of speckle patterns //Progress in Optics.
1979,V.14, P.3-49.
24. Гудмен Дж. Статистическая оптика / Пер. с англ. М.: Мир,
1988. 528с.
25. Bennet H.E., Porteus J.O. Relation Between Surface Roughness and Specular Reflection at Normal Incidence // JOSA. 1961. V.51. N. 2. P.123-129.
26. Сахновский М.Ю. Регулярное отражение (пропускание) излучения шероховатыми поверхностями и его использование для контроля качества зеркал // Опт. и спектр. 1985. Т.58. B.I. С.130-134.
27. Fujii H., Asakura Т., Shindo Y.. Measurements of surface roughness properties by means of laser techniques. // Opt. Comm. 1976. V.I 6. N.1. P.68-72.
28. Angelsky O.V., Maksimyak P.P. Optical diagnostics of random phase objects // Appl. Opt. 1990. V.29. N.19. P.2894-2898.
29. Ангельский О.В. Корреляционная диагностика случайных пространственно-неоднородных оптических полей //Квант, электр. 1992.T.19.N.12. С.1151-1158.
30. Ангельский О.В., Житорюк В.Г., Максимяк П.П. О возможности корреляционно-оптического исследования фазово-неоднородных статистических поверхностей // Опт. и спектр. 1986. Т.60.В.5. С.1013-1017.
31. Ангельский О.В., Курск Г.К., Магун И.И., Максимяк П.П. Исследование статистических моментов амплитуды и фазы поля оптического излучения, рассеянного хаотическим фазовым экраном
// Опт. и спектр. 1989. Т.66. В.4. С.835-838.
32. Рябухо В.П. Интерференция частично развитых спекл-полей // Опт. и спектр. 1995. Т.78. В.6. С.970-977.
33. Рябухо В.П., Чаусский А.А. Интерференция спекл-полея в зоне дифракции сфокусированного пространственно-модулированного лазерного пучка на случайном фазовом экране //Письма в ЖТФ. 1995. Т.21. В.16. С.57-62.
34. Ryabukho V.P., Khomutov V.L, Arshuk O.A., Chaussky A.A., Terent'eva I.F. Light interference in diffraction field of spatially modulated laser beam behind random phase object // Proc. SPIE:
Holography and Correlation Optics. 1995. V.2647. P.63-74.
35. Рябухо В.П., Аветисян Ю.А., Суманова А.Б. Дифракция пространственно-модулированного лазерного пучка на случайном фазовом экране // Опт. и спектр. 1995. Т.79. В.2. С.299-306.
36. Рябухо В.П., Аветисян Ю.А., Голубенцева Л.И., Зимняков Д.А. Корреляционные эффекты при освещении рассеивающих сред лазерным пучком с интерференционной структурой // Голография:
теоретические и прикладные вопросы. Долгопрудный: МФТИ, 1994.С.52-61.
37. Ryabukho V.P., Chaussky A.A., Khomutov V.L., Tuchin V.V„ Terent'eva I.F. Interferometric testing of the random phase objects (biological tissue models) by spatially-modulated laser beam // Proc. SPIE: CIS Selected papers "Coherence-Domain Methods in Biomedical Optics". V.2732, 1996. P.100-117.
38. Рытов С.М., Кравцов Ю.А., Татарский Б.И. Введение в статистическую радиофизику. Ч.11: Случайные поля. М.: Наука, 1978. 463с.
39. Топорец А.С. Оптика шероховатой поверхности. Л.: Машиностроение, 1988.191с.
40. Ogitvy J.A., Foster J.R., Rough surfaces: gaussian or exponential statistics//J. Phys. D: Appl. Phys. 1989. V.22. P.1243-1251.
41. Graegorzewski B. Young's interference experiment in the study of partically developed speckle // Optik 1989. V.82. N.3. P.75-81.
42. Горбатенко Б.Б., Клименко И.С., Максимова Л.А., Рябухо В.П. О некоторых статистических свойствах разности фаз в развитом спекл-модулированном поле//Опт. и спектр. 1995. Т.78. В.2 . С.316-319.
43. Власов И.Г., Скроцкий Г.В., Соловьев Е.Г. Исследование когерентности дифракционным интерферометром сдвига //Кв. электр. 1972. N.3. С.84-86.
