А.М.ИВАНОВА, А.А.КОВАЛЕНКО, С.П.КОТОВА,
Н.Л.КУПРИЯНОВ, В.М.ПЕТРОПАВЛОВСКИЙ
ОПРЕДЕЛЕНИЕ ОПТИЧЕСКИХ ХАРАКТЕРИСТИК
СИЛЬНОРАССЕИВАЮЩИХ СРЕД С
ИСПОЛЬЗОВАНИЕМ МЕТОДА МОНТЕ-КАРЛО
Введение
Для диагностики состояния биотканей, разработки научно-обоснованных процедур лазерной терапии, лазерного синтеза трехмерных изделий важна информация о поведении светового поля в сильнорассеивающей среде [1,2]. Для определения интенсивности света внутри и вне рассеивающей среды наиболее приемлемым является подход, основанный на применении теории переноса излучения [3,4]. Из существующих практически значимых методов решения уравнения переноса излучения наиболее универсальным является метод численного моделирования Монте-Карло [5]. Он может быть применен для любой геометрии и для любой (однородной или неоднородной) среды. Его основной недостаток -большие затраты машинного времени. Но в связи с быстрым развитием вычислительных средств данный метод становится реальным инструментом для решения подобных задач. Для математического описания свойств рассеивающей среды обычно пользуются следующими понятиями: μα и μs - коэффициенты поглощения и рассеяния, которыми обозначают вероятность того, что на единице пути в среде фотон будет поглощен и рассеян; р(6) -угловое распределение рассеяния или фазовая функция (6 -угол между падающим и рассеянным фотонами в плоскости рассеяния):
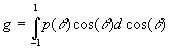
-средний косинус рассеяния (для изотроп-
ного рассеяния
g=0). При известных коэффициентах поглощения и рассеяния, фазовой функции рассеяния, показателя преломления среды с помощью метода Монте-Карло могут быть определены распределения рассеянного и прошедшего излучения как внутри среды, так и вне ее. Тем самым решается, например, задача дозиметрии при лазерном облучении, устанавливается зависимость между измеренными и искомыми параметрами в диагностике.
Однако оптические параметры тканей для многих длин волн, в частности, из ближней ИК - области (0.7-1.5мкм) либо неизвестны, либо значения, полученные разными авторами, сильно
отличаются и требуют уточнения. Отсюда возникает необходимость их определения. При этом интерес представляет разработка методов, позволяющих определить параметры среды неинвазивным способом, например, по характеристикам рассеянного назад света. Это важно, например, для диагностики живых тканей. В известных методах измерения указанных характеристик, как правило, используют специально подготовленные слои образцов [6].
В последнее время в задачах диагностики биотканей получил развитие метод определения оптических характеристик, основанный на сопоставлении результатов численного моделирования уравнения переноса излучения в рассеивающей среде методом Монте-Карло и экспериментально измеренных характеристик рассеяния и пропускания света [7]. Фактически речь идет об обратной математической
задаче для уравнения переноса света при его решении методом Монте-Карло. Для реализации этого подхода в каждом конкретном случае необходимо решить ряд вопросов:
определить, в каких случаях связь между параметрами однозначна, каков вид зависимости для конкретной геометрии измерений, какова должна быть точность измерений и др.
Данная работа посвящена определению коэффициента поглощения и транспортного коэффициента рассеяния по измеренным интегральным характеристикам отражения и пропускания сильнорассеивающих сред. В качестве модельной среды в экспериментах использовались металл-полимерные порошковые композиции, предназначенные для лазерного синтеза объемных изделий.
Расчет характеристик отраженного и прошедшего света
Расчет проводился методом Монте-Карло для двух моделей:
полубесконечной среды (рис.1,а) и ограниченной плоскопараллельной среды (рис. 1 ,б).
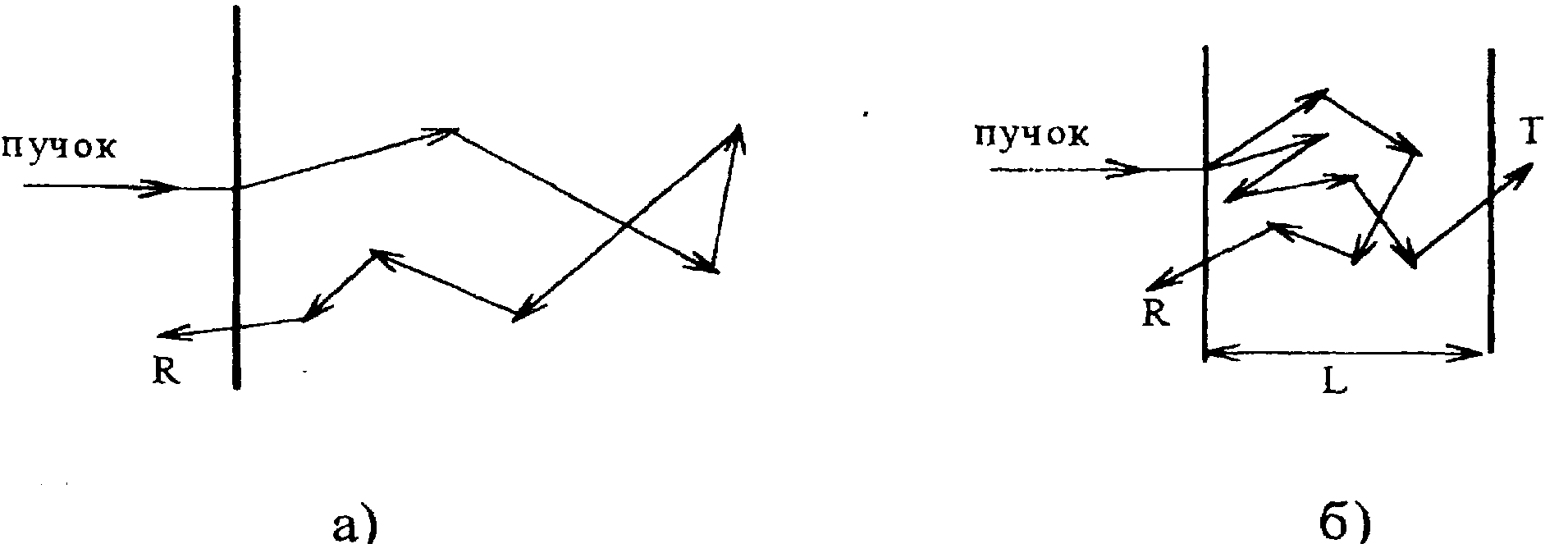
Рис. 1 Модели, используемые в расчетах: а) - однородная полубесконечная среда; б) -однородный слой толщины
L
Метод Монте-Карло основан на численном моделировании транспорта фотонов. Фотоны падают перпендикулярно среде. На каждом шаге моделирования, в зависимости от оптических характеристик среды, вычисляются длина свободного пробега фотона , его случайное направление и определяется вероятность поглощения, рассеяния и вылета фотона из средах. Судьба каждого фотона разыгрывается до тех пор, пока фотон либо не поглотится, либо не вылетит из среды. Случайное направление фотона определяется в соответствии с фазовой функцией рассеяния р(θ). Для большинства биотканей фазовая функция описывается формулой Хэни-Гринштейна:
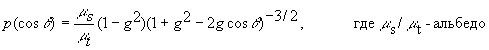
Для ускорения расчетов может быть использовано так называемое транспортное приближение, при котором анизотропное рассеяние заменяется изотопным, а среда характеризуется транспортным коэффициентом рассеяния
μs'=μs(l-g)
и ослабления μt'==μt(l-g).
Средняя длина свободного пробега фотона Λ=1/μt' [8].
На рис.2 представлены результаты выполненных нами расчетов интегрального коэффициента отражения
R в зависимости от среднего косинуса угла рассеяния, полученные с использованием функции Хэни-Гринштейна и транспортного приближения. Из графиков видно, что для реальных сильнорассеивающих сред (μα/μs<<1)
можно пользоваться изотропным рассеянием и транспортным альбедо.
Расчетным способом были определены интегральные коэффициенты отражения и пропускания в зависимости от транспортного альбедо и толщины слоя, функции распределения интенсивности обратно? ассеянного света в зависимости от расстояния от центра среды и распределения
интенсивности внутри ткани вдоль оси z.
На рис.3 представлен график зависимости коэффициента диффузного отражения от транспортного альбедо для случая полубесконечной среды. С целью тестирования программы вычисленные зависимости были сравнены с литературными данными [4]. Отметим, что величина отражения не зависит от Λ
.
На рис.4 представлен график зависимости коэффициента пропускания Т от толщины слоя при фиксированном значении транспортного альбедо. Все расчеты проведены для условий отсутствия скачка преломления на границе и случая точечного источника.
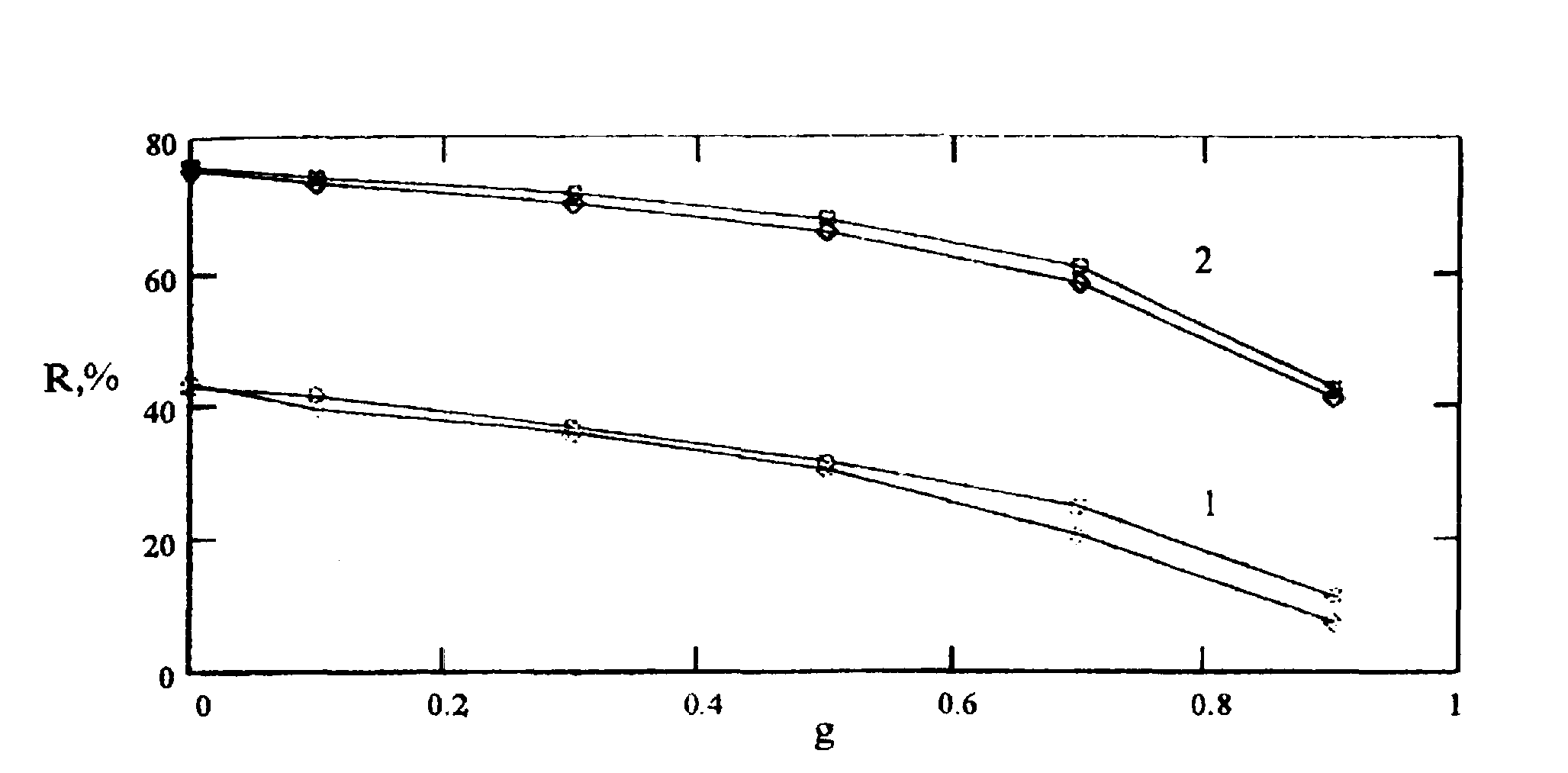
Рис.2 Зависимость коэффициента диффузного отражения R от среднего косинуса угла рассеяния с использованием функции Хэни-Гринштейна („
) и транспортного приближения (
◊) для двух значений μα/μs: 1 -
μα/μs =0.1; 2 -
μα/μs=0.01
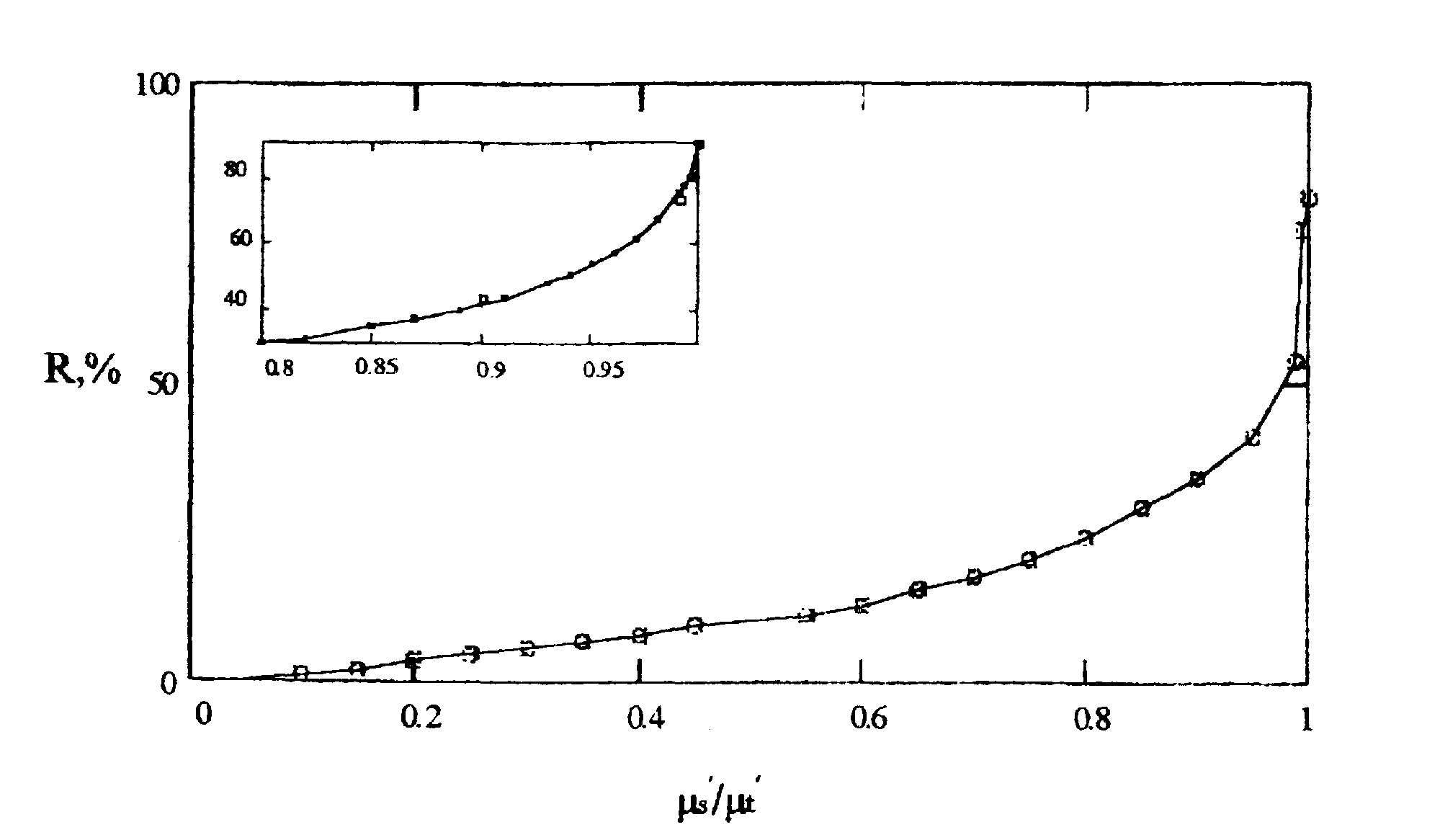
Рис.3 Зависимость коэффициента диффузного отражения R от
транспортного альбедо
μα'/μs'. Значки „
соответствуют данным, взятым из [4]
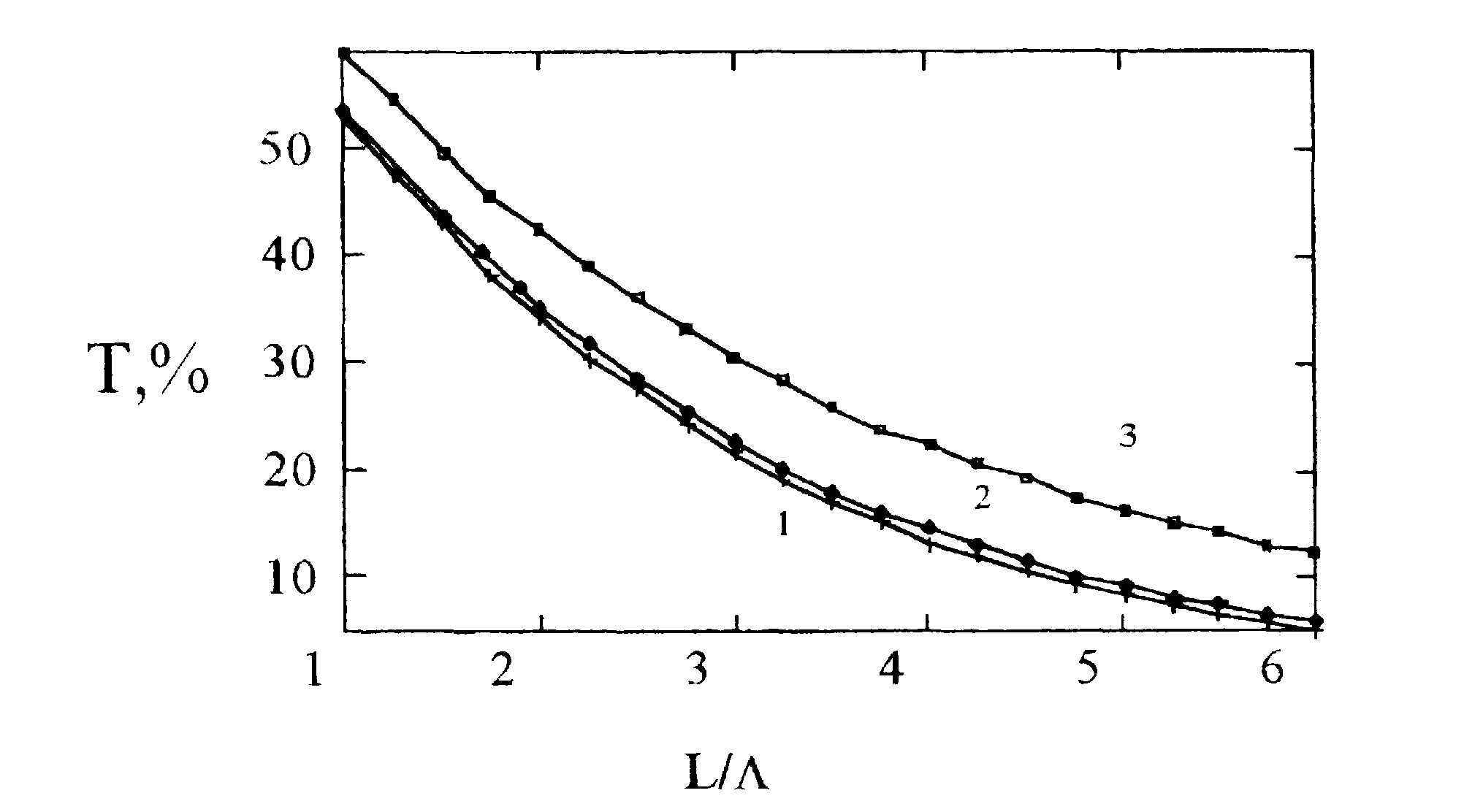
Рис
.4 Зависимость коэффициента пропускания Т от толщины слоя при значениях транспортного альбедо μα'/μs': 1 - μα'/μs'=0.91, 2- μα'/μs'=0.92, 3- μα'/μs'=0.97
Эксперимент
В экспериментах измерялись характеристики порошковых сред, содержащих металлические (латунь) и полимерные (поликарбонат) частицы в различных соотношениях. Для измерения интегрального коэффициента отражения R использовался фотометр отражения ФО-1 (спектральный диапазон от 400 до 930нм). Порошок насыпался в кювету глубиной 5мм. Слой такой толщины можно считать бесконечным, что подтверждается расчетами и экспериментами. Результаты измерений для длины волны 830нм представлены в таблице 1 (с. 32).
Измерение интегрального коэффициента пропускания Т проводилось на длине волны полупроводникового лазера ИЛ ПН-108 (λ=830нм). Для создания тонких слоев известной толщины для каждого вида смеси были изготовлены засыпные клинья, представляющие собой две скрепленные между собой стеклянные пластины, с одной стороны между которыми положена прокладка, и внутрь образовавшегося клина засыпана исследуемая смесь. Таким образом можно получить любое количество замеров для каждого вида смеси на слоях практически любой толщины, начиная от толщины. равной минимальному размеру частиц.
Образец освещался сфокусированным лазерным пучком. Непосредственно за образцом устанавливался фотодиод с диаметром светочувствительной площади 8мм (ФД-24К). Образец перемещался перпендикулярно лучу с помощью микрометрической подвижки. Графики пропускания для порошка с содержанием 47.6 % латуни в зависимости от толщины слоя представлены на рис 5.
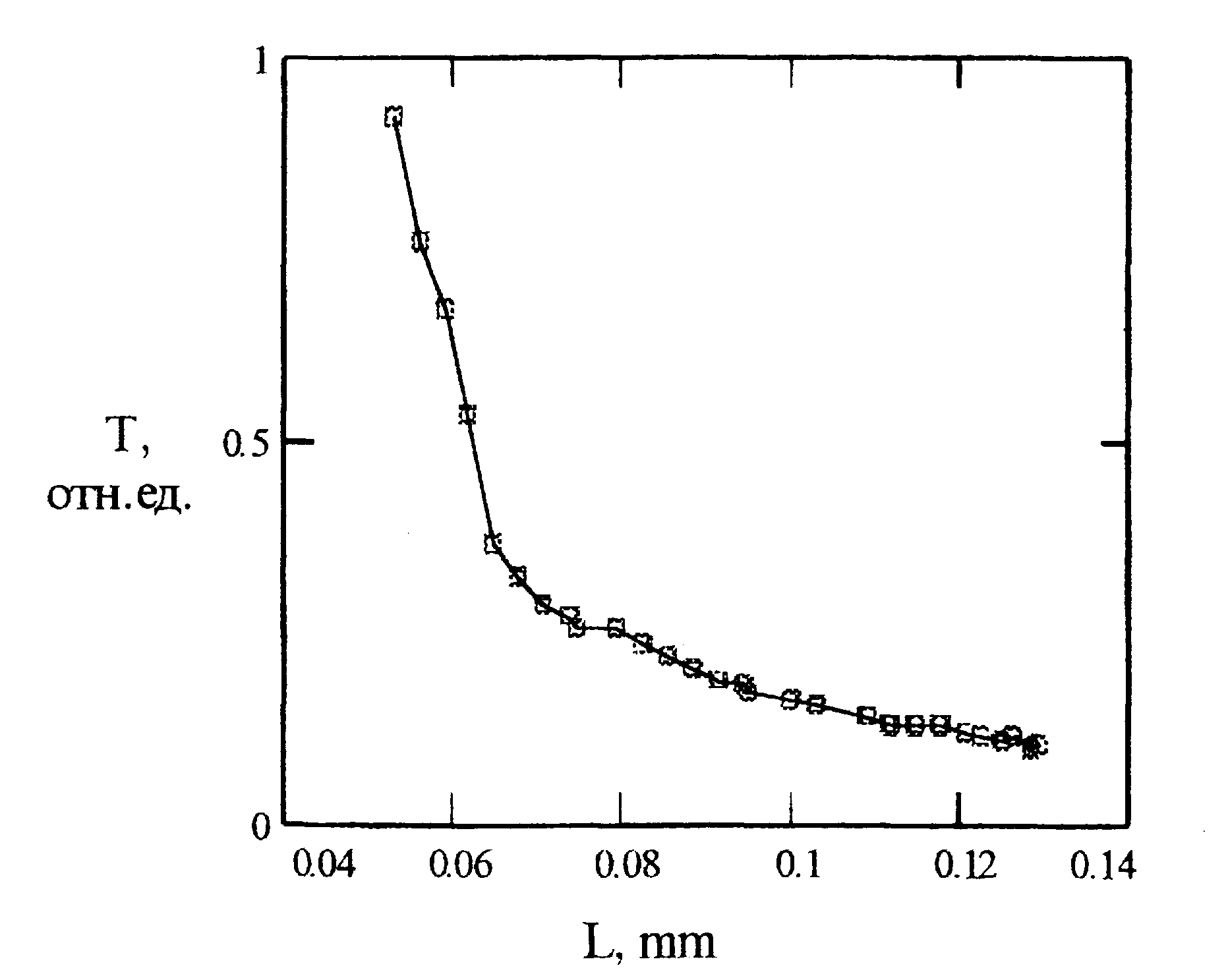
Рис.5 Экспериментальная зависимость пропускания порошка с содержанием латуни 47.6% от толщины слоя
Определение оптических параметров
Процедура определения коэффициента поглощения μα', и транспортного коэффициента рассеяния μs' заключалась в следующем. По измеренным значениям интегрального коэффициента отражения (табл. 1, столбец 2) определялось альбедо μα'/μs' (табл. 1, столбец 3) для каждой среды в соответствии с вычисленной зависимостью R(μα'/μs') (рис.3). Для ряда экспериментальных значений
коэффициента пропускания при известных толщинах (табл.1, столбец 4) в соответствии с расчетными зависимостями пропускания T(L/λ) (рис.4) были получены длины свободного пробега фотона Λ=1/(μα+μs'). Из полученных значений μα'/μs' и и Λ вычислены искомые значения μs' и μα'. Результаты представлены в таблице 1.
Параметры рассеивающих сред Таблица 1
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
состав % |
R,
% |
μ s'/μt' |
l,
мкм |
T,
% |
Λ,
мкм |
<Λ> ,
мкм |
μ s', мм-1 |
μα,
мм -1 |
|
47.6 |
45 |
0.92 |
100
125 |
16.6 10 |
26.3
25.5 |
25.8 |
35.7 |
3.1 |
|
86 |
42.5 |
0.91 |
100
125 150 |
13
9.2 4.8 |
25
26 25.4 |
25.5 |
35.7 |
3.5 |
|
3.9 |
65 |
0.97 |
100 125 150 |
36
32
26 |
38.5 43.1 42.9 |
41.5 |
23.4 |
0.7 |
*
Указано процентное содержание металлических частиц по насыпному объему.
Проверка правильности полученных значений
μs'
и μα может быть выполнена путем проведения дополнительных измерений и их сравнения с расчетными зависимостями. На рис.6,7 приведены расчетные зависимости распределения интенсивности излучения внутри среды вдоль координаты z и на поверхности среды в зависимости от расстояния от центра пятна для найденных значений μs' и μα.
Из предварительных экспериментов по измерению радиуса пятна рассеянного назад света следует, что измеренный и вычисленный радиусы пятен совпадают по порядку величины.
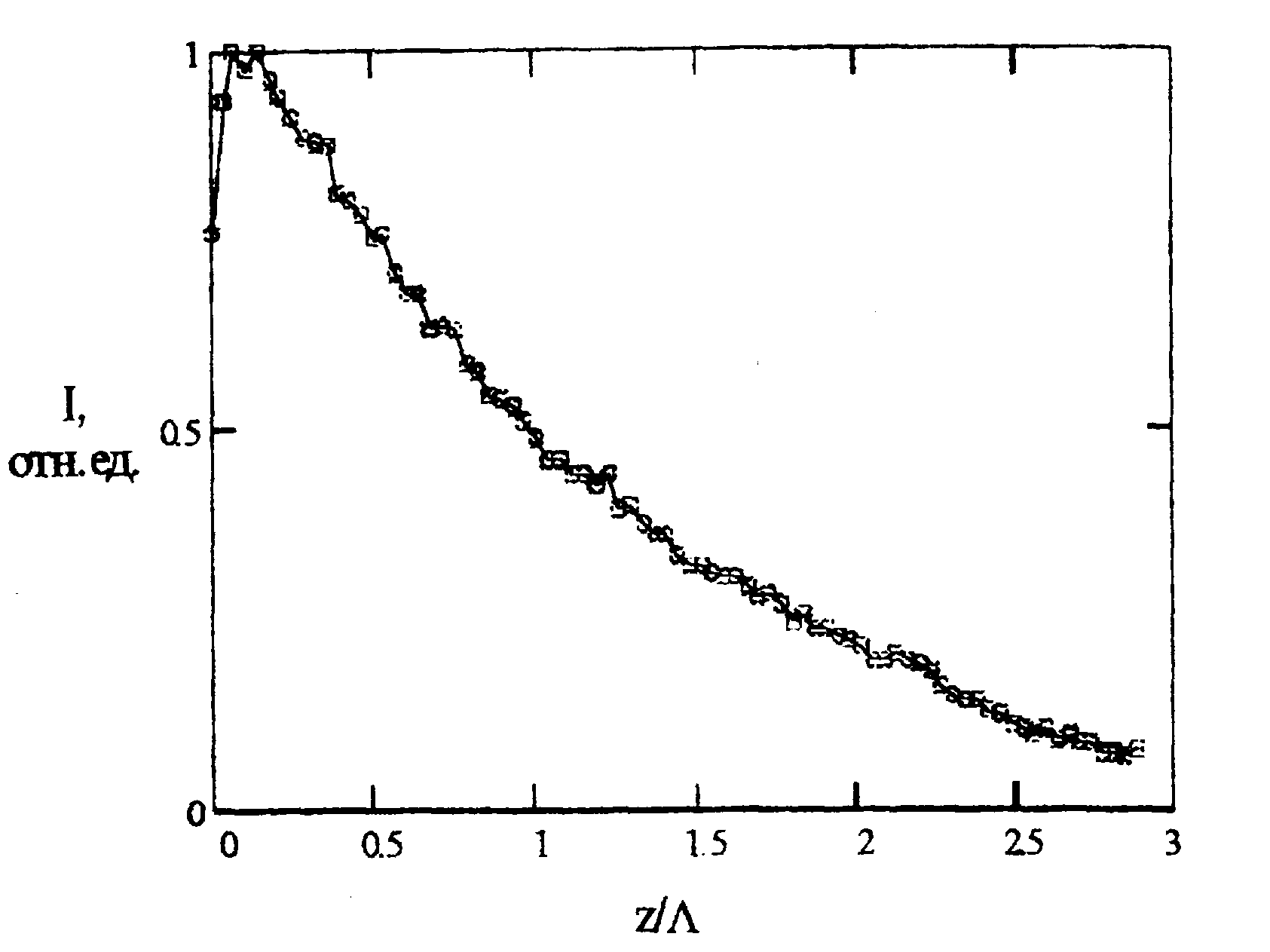
Рис.6 Распределение интенсивности излучения в среде от координаты z для
μs' =35.7мм-1, μα=3.1мм-1
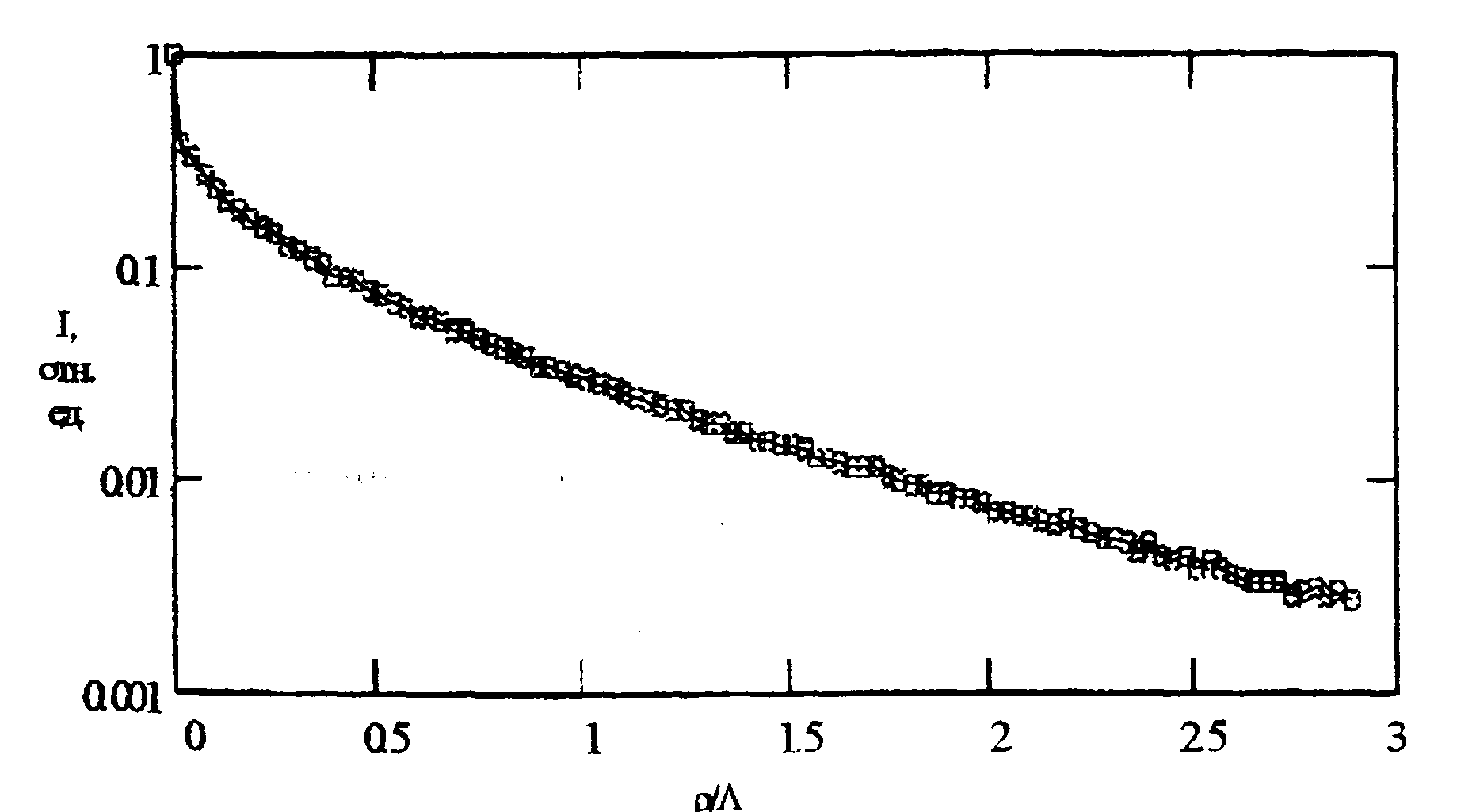
Рис. 7 Распределение интенсивности рассеянного назад света на поверхности среды от расстояния ρ до центра падения пучка для
μs'=3 5.7мм-1, μα=3.1мм-1
Заключение
Разработана методика определения коэффициента поглощения и транспортного коэффициента рассеяния для сильнорассеивающих сред , основанная на сопоставлении результатов численного моделирования уравнения переноса излучения методом Монте-Карло и экспериментально измеренных интегральных характеристик диффузного отражения и пропускания. Методика включает следующие этапы:
- определение путем численного моделирования зависимости между искомыми параметрами и экспериментально измеряемыми величинами для используемой геометрии опыта;
- измерение интегральных коэффициентов диффузного отражения и пропускания;
- расчет искомых величин по полученным зависимостям.
Показана работоспособность методик на примере определения коэффициентов поглощения и рассеяния металл-полимерных порошковых композиций.
Литература
1. Тучин В. В. Основы взаимодействия низкоинтенсивного лазерного излучения с биотканями: дозиметрический и диагностический аспекты //Изв. акад. наук, сер.физ. 1995. Т.59. № 6, С. 120-143.
2. Труды конференции "Лазер - 95".Мюнхен, июнь, 1995.
3. Воробьев Н.С. Оптические свойства головного мозга// Препринт №31.1991.
4. Словецкий С.Д. Моделирование распространения оптического излучения в слоистой случайно-неоднородной среде методом Монте-Карло // Радиотехника. 1994. № 7.
5. Иванов А.П. Оптика рассеивающих сред. Минск: Наука и техника. 1969.
6. Cheong W.F.,
Ргаhl S.A., Welch A.J. A review of the Optical Properties of Biological Tissues // IEEE Jour. of QE. 1990. У.26. №12.
7. Marquet P., Brvilacqua F., Depeursinge C. Determination of redused scattering and absorbtion coefficients by a single charge-coupled-device array measurement//Opt.Eng.
1995. V. 34. № 7. Р.2055-2069.
8. Hock S.T., Wilson B.S., Patterson M.S., Wyman D.R. Monte-Carlo modeling of light propagation in highly scattering tissues // IEEE Trans.Biomed.Eng. 1989. V.36. P.I 162-1168.

