H.Г . ВЛАСОВ, А.Е.ШТАНЬКО
О ВОЗМОЖНОСТЯХ РАЗВИТИЯ МЕТОДОВ ВОССТАНОВЛЕНИЯ ИЗОБРАЖЕНИЙ НА ОСНОВЕ ЭФФЕКТА ЛАУ
Эффект Лау [1] заключается в периодической модуляции спектров, даваемых парой дифракционных решеток одинакового периода, расположенных параллельно друг Другу на небольшом расстоянии. Полосы, модулирующие спектры, включая нулевой порядок дифракции, локализованы на бесконечности и наблюдаются на фоне протяженного источника. В нулевом порядке дифракции они ахроматичны и имеют достаточно хороший контраст. Появление этих полос можно объяснить, например, эффектом муара двух решеток. В зависимости от направления наблюдений штрихи этих решеток могут накладываться в фазе, пропуская излучение, или в противофазе, перекрывая его.
Эффект Лау первоначально был обнаружен для низкочастотных решеток. Позднее его получили с помощью низкочастотных голографических решеток, причем была получена высокая частота полос, модулирующих спектры [2]. Эффект Лау, наблюдаемый на таких высокочастотных решетках, достаточно полно может быть описан как результат интерференции двукратно дифрагировавших на решетках волн. Рис.1 поясняет образование этих волн: +1 -и порядок дифракции на первой решетке, дифраги-руя на второй решетке в -1-й порядок дифракции, вновь распространяется по направлению падающей волны. Аналогично -1-й порядок дифракции на первой решетке дифрагирует на второй решетке в +1-й порядок. Обе двукратно дифрагированные волны распространяются по одному направлению с некоторым поперечным сдвигом по отношению друг к другу, который зависит от частоты решеток и от величины зазора между ними. Такие волны, как известно [З], образуют интерференционную картину эквидистантных прямолинейных полос, локализованных в бесконечности. Если решетки имеют достаточно высокую дифракционную эффективность, наблюдаемая картина полос имеет хороший контраст.
Ахроматичность интерференционных полос, получаемых с помощью эффекта Лау, а также возможность наблюдения их в свете протяженного источника делает привлекательной идею создания на его основе методов оптической обработки и записи информации в некогерентном или частично- когерентном излучении.
Настоящая работа посвящена оценке возможности осуществления записи и восстановления изображений с использованием оптического преобразования Фурье на основе эффекта Лау, а также возможности регистрации с его помощью функции пространственной когерентности излучения.
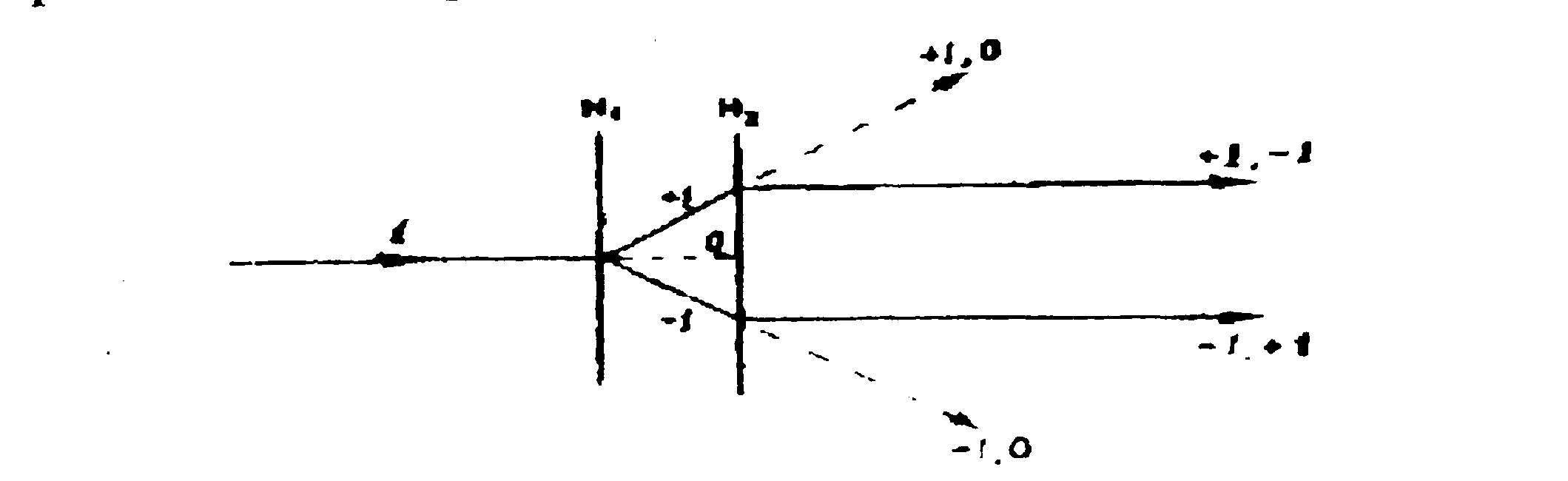
Рис. 1. Образование двукратно дифрагированных волн на паре решеток H1, Н2. 1 - падающая волна
Идея использования эффекта Лау для оптического преобразования Фурье в общем виде заключается в следующем.
Оптический образ в виде самосветящегося объекта или освещенного пространственно некогерентным излучением транспаранта наблюдают через пару решеток. При этом интерференционные полосы, возникающие вследствие эффекта Лау, модулируют изображение объекта, что математически можно представить как произведение распределения интенсивности по объекту I(х) на модулирующую функцию вида а + b cos ωх (рассматриваем для простоты одномерный случай), описывающую интерференционные полосы. Рассмотрим второе слагаемое I(х) b cos ωx в этом произведении. Оно интересно тем, что I(x) b cos ωx dx представляет собой Фурье- образ объекта. Если фотоприемник, расположенный позади решеток, интегрирует излучение, поступающее от всех точек объекта, то воспринимаемый им сигнал содержит Фурье компоненту F(ω) исходного образа I(х). Правда, таким способом можно зарегистрировать лишь одну Фурье- компоненту, а не Фурье-образ.
Рассмотрим теперь более сложный случай - эффект Лау, даваемый парой голографических решеток, обладающих фокусирующими свойствами. Такие решетки по структуре представляют собой зонные пластинки Френеля или их внеосевые фрагменты. Пусть они расположены соосно и параллельно друг другу.
Характер интерференционных полос, наблюдаемых через такую пару решеток в свете протяженного источника, зависит от
положения точки наблюдения. Смещение наблюдателя будет вызывать изменение картины полос из-за кажущегося взаимного смещения решеток вследствие их параллакса. При выполнении определенных соотношений между фокальными расстояниями решеток, величиной зазора между ними и расстоянием до плоскости наблюдения можно из различных точек этой плоскости наблюдать интерференционные картины в виде прямолинейных полос различной ориентации и периода. Найдем эти соотношения.
Пусть имеется пара соосных решеток H1 и H2 в виде зонных пластинок Френеля, расположенных на расстоянии D друг от друга (см. рис.2). Для простоты будем учитывать только +1-е порядки дифракции на решетках. Рассмотрим сходящуюся сферическую волну с центром в некоторой точке zo на общей оси решеток. В результате дифракции этой волны на решетке H1 в +1-x порядках возникнут две сферические волны различной кривизны, каждая из которых продифрагирует на решетке Н2. Мы рассмотрим пару двукратно дифрагированных волн, образованных сочетанием +1-го порядка дифракции на решетке H1 с -1-м порядком дифракции на решетке Н2 и -1-го порядка дифракции на решетке H1 с -4-1-м порядком дифракции на решетке Н2. Найдем условия, при которых обе эти волны будут иметь одинаковую кривизну, то есть сойдутся в общем центре.
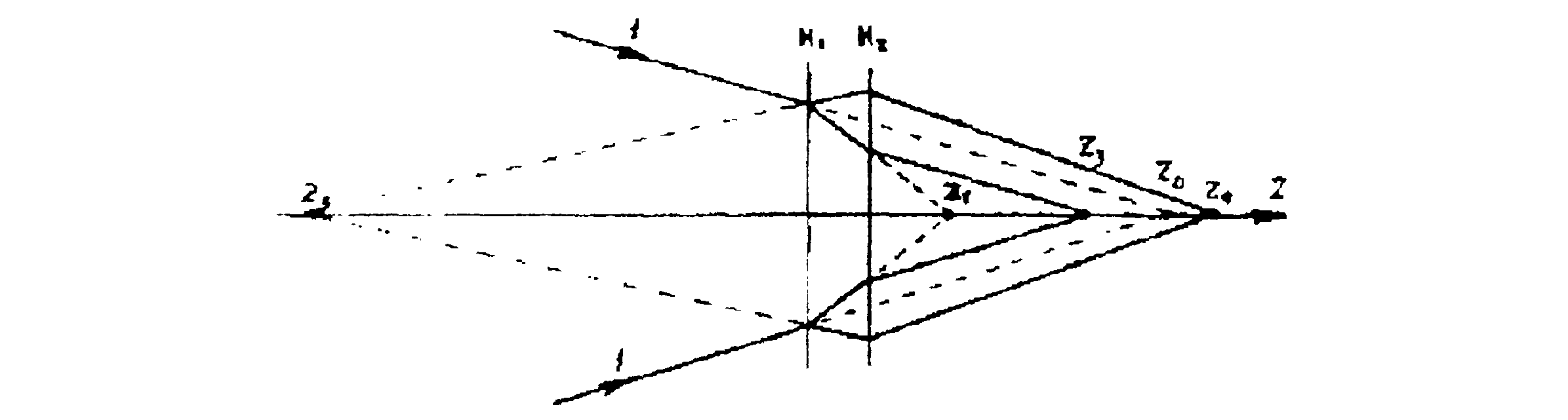
Рис. 2. Схема дифракции сферической волны 1 на паре фокусирующих решеток H1, Н2.
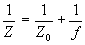 Для зонной пластинки справедлива формула линзы, связывающая координаты восстанавливающего источника zo с координатами z1 и z2 его изображений, построенных в +1-м и -1-м порядках дифракции соответственно (начало координат находится в точке пересечения зонной пластинки с осью Z). Для решетки H1.
Для зонной пластинки справедлива формула линзы, связывающая координаты восстанавливающего источника zo с координатами z1 и z2 его изображений, построенных в +1-м и -1-м порядках дифракции соответственно (начало координат находится в точке пересечения зонной пластинки с осью Z). Для решетки H1.
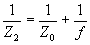 где f - фокусное расстояние решетки Hi в 1-м порядке дифракции.
где f - фокусное расстояние решетки Hi в 1-м порядке дифракции.
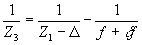 Две сферические волны с центрами z1 и z2, полученные в результате дифракции на решетке H, являются восстанавливающими для решетки Н2. Координаты изображений z3 и z4, построенных этой решеткой, в системе координат, связанной с решеткой H1, будут определяться соотношениями.
Две сферические волны с центрами z1 и z2, полученные в результате дифракции на решетке H, являются восстанавливающими для решетки Н2. Координаты изображений z3 и z4, построенных этой решеткой, в системе координат, связанной с решеткой H1, будут определяться соотношениями.
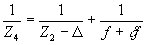 где δf - разница между фокусами решеток H1 и Н2.
где δf - разница между фокусами решеток H1 и Н2.
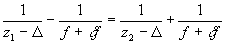 Мы ищем условия, при которых волны, двукратно дифраги-рованные на решетках H1 и Н2, имеют одинаковую кривизну, то есть требуем, чтобы z3 = z4. Тогда
Мы ищем условия, при которых волны, двукратно дифраги-рованные на решетках H1 и Н2, имеют одинаковую кривизну, то есть требуем, чтобы z3 = z4. Тогда
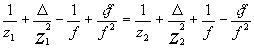 Будем полагать, что z1 > Δ, z2 > Δ θ f > δf. Β этих предположениях уравнение (5) может быть записано следующим образом
Будем полагать, что z1 > Δ, z2 > Δ θ f > δf. Β этих предположениях уравнение (5) может быть записано следующим образом
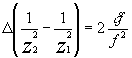 С учетом (1) и (2) выражение (6) упрощается
С учетом (1) и (2) выражение (6) упрощается
Если учесть вытекающие из (1) и (2) соотношения

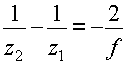
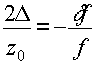
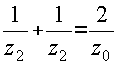 выражение (7) приобретает вид
выражение (7) приобретает вид
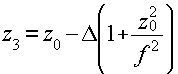 Выполнение условия (10) обеспечивает совпадение кривизн обеих двукратно дифрагированных на решетках волн. Используя соотношение (10), с помощью формул (3) и (1) можно вычислить координату Z3 центра этих сферических волн.
Выполнение условия (10) обеспечивает совпадение кривизн обеих двукратно дифрагированных на решетках волн. Используя соотношение (10), с помощью формул (3) и (1) можно вычислить координату Z3 центра этих сферических волн.
Следует отметить, что полученный результат справедлив не только для осевой точки гз, но и для всей плоскости z = z3. Это вытекает из того, что исходные формулы линзы (1), (2), если не рассматривать аберрации, справедливы и для внеосевых точек в пространстве предметов и изображений.
Таким образом, координата z3 определяет положение плоскости z = z3, при наблюдении из которой кривизны обоих двукратно дифрагированных на решетках волн совпадают. Эти волны, полученные делением общей первоначальной сферической волны, взаимно когерентны и образуют интерференционную картину.
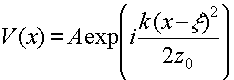 Для описания этой картины рассмотрим процесс прохождения через решетки внеосевой сферической волны V(x), сходящейся в произвольную точку с координатой ξ в плоскости z = z0. Распределение комплексной амплитуды этой волны в плоскости первой решетки представим как
Для описания этой картины рассмотрим процесс прохождения через решетки внеосевой сферической волны V(x), сходящейся в произвольную точку с координатой ξ в плоскости z = z0. Распределение комплексной амплитуды этой волны в плоскости первой решетки представим как
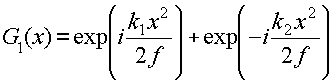 где k - волновое число, А - амплитуда волны (для простоты рассматриваем плоский случай). Комплексное пропускание G1 первой решетки в +1 -х порядках дифракции можно представить
где k - волновое число, А - амплитуда волны (для простоты рассматриваем плоский случай). Комплексное пропускание G1 первой решетки в +1 -х порядках дифракции можно представить
где k1 - волновое число волны, использованной при записи решеток H1 и H2 (предполагаем, что решетки изготовлены голографическим путем), f - фокусное расстояние решетки H1 для волны с волновым числом k1.
Перемножая V(x) и G1(x), мы получим распределение комплексной амплитуды дифрагированных волн сразу за решеткой H1. Далее следует учесть изменение кривизны этих волн на величину А зазора между решетками Н1 и Н2 и перемножить полученные распределения амплитуды волн на комплексное пропускание G2 второй решетки. В результате получим распределения амплитуд V1 и V2 двух интерферирующих волн сразу за второй решеткой. Мы приводим конечный результат, опуская громоздкие промежуточные преобразования
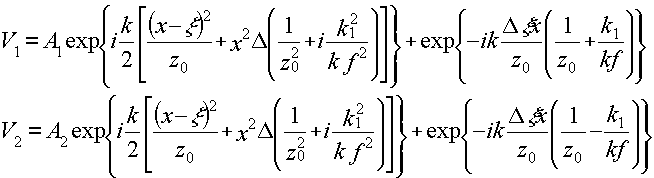
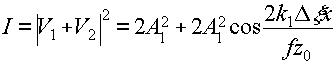 Волны V1 и V2 представляют собой две сферические волны, сходящиеся в плоскости z = z3 вблизи точки ξ,. Эти волны отличаются друг от друга лишь вторыми экспонентами, фаза которых линейно зависит от х. Интерферируя, эти волны образуют распределение интенсивности I
Волны V1 и V2 представляют собой две сферические волны, сходящиеся в плоскости z = z3 вблизи точки ξ,. Эти волны отличаются друг от друга лишь вторыми экспонентами, фаза которых линейно зависит от х. Интерферируя, эти волны образуют распределение интенсивности I
имеющее вид прямолинейных эквидистантных полос, пространственная частота которых ω, равная
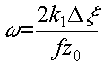 пропорциональна координате ξ, то есть величине смещения точки наблюдения от оси z. Следует отметить, что величина ω не зависит от длины волны, так как входящие в (17) величины k1 и f являются величинами, фиксированными при записи решеток H1 и H2. Таким образом, наблюдаемые интерференционные полосы будут ахроматическими.
пропорциональна координате ξ, то есть величине смещения точки наблюдения от оси z. Следует отметить, что величина ω не зависит от длины волны, так как входящие в (17) величины k1 и f являются величинами, фиксированными при записи решеток H1 и H2. Таким образом, наблюдаемые интерференционные полосы будут ахроматическими.
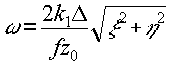 Для простоты мы рассматривали лишь одномерный объект. Нетрудно показать, что в общем случае интерференционная картина, наблюдаемая в плоскости z = z3, будет представлять собой эквидистантные параллельные полосы, перпендикулярные линии, соединяющей точку наблюдения с точкой z3. Пространственная частота этих полос равна
Для простоты мы рассматривали лишь одномерный объект. Нетрудно показать, что в общем случае интерференционная картина, наблюдаемая в плоскости z = z3, будет представлять собой эквидистантные параллельные полосы, перпендикулярные линии, соединяющей точку наблюдения с точкой z3. Пространственная частота этих полос равна
где x,h - координаты в плоскости наблюдения.
Описанная выше интерференционная картина является проявлением эффекта Лау, полученного парой решеток в виде зонных пластинок.
Итак, мы установили, что при наблюдении через пару соосных зонных пластинок из некоторой плоскости, положение которой определяется соотношением (11), распределение интенсивности по объекту вследствие эффекта Лау оказывается промодулирован-ным по косинусоидальному закону, причем, меняя точку наблюдения, можно менять пространственную частоту и ориентацию модулирующих полос. Эти свойства позволяют осуществить преобразование Фурье от распределения интенсивности по объекту.
Действительно, найдем распределение интенсивности I1 в плоскости наблюдения z = zз, вызываемое объектом, имеющим распределение интенсивности I0 и расположенным в плоскости первой решетки H1. На основании (16) с точностью до постоянного множителя
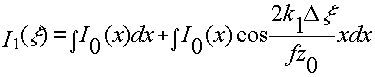 Второе слагаемое представляет собой косинусоидальный интеграл
Второе слагаемое представляет собой косинусоидальный интеграл
Фурье от распределения интенсивности по объекту I0(х). то есть плоскость наблюдения z = z0 является Фурье плоскостью по отношению к плоскости объекта H1. Задача состоит в том, чтобы выделить указанное слагаемое из общей суммы I1(ξ). Физически это возможно сделать, если управлять фазой модулирующих интерференционных полос. Пусть I1(ξ) - исходное распределение интенсивности в плоскости наблюдения, a I1( ξ) - распределение интенсивности в этой плоскости, полученное при изменении фазы модулирующих полос на π. Тогда на основании (19)
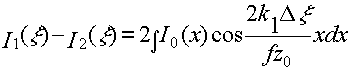
Tаким образом, разность двух распределений интенсивности I1-I2 пропорциональна косиносному интегралу Фурье от распределения интенсивности по объекту I0.
Аналогичным образом можно получить и значение синусного интеграла Фурье. Для этого нужно изменить фазу модулирующих интерференционных дважды: на π /2 и З π /2, а затем вычесть полученные при этом распределения интенсивности в плоскости наблюдения.
Физически менять фазу модулирующих полос без изменения их частоты возможно лишь путем изменения начальной фазы полос, составляющих структуру одной из решеток H1 или Н2. Например, можно разделить решетку H1 на 4 сектора, в каждом из которых начальная фаза полос отличается на π /2 от фазы полос в соседнем секторе. При вращении этой решетки вокруг оси Z сектора последовательно будут устанавливаться против решетки Н2 и фаза модулирующих полос будет меняться на π /2 при каждой смене сектора. При этом в соответствующие моменты времени необходимо регистрировать распределения интенсивности в плоскости наблюдения. Такая регистрация может осуществляться матрицей фотоприемников, сопряженных с компьютером, проводящим последующую обработку информации.
Таким образом на основе эффекта Лау, получаемого с помощью пары решеток типа зонных пластинок, можно в простран-ственнонекогерентном полихроматическом излучении регистрировать преобразование Фурье от распределения интенсивности по объекту. Этот процесс является некоторым аналогом процесса записи голограммы Фурье, только на голограмме регистрируется
информация о распределении комплексной амплитуды по объекту, а в нашем случае - о распределении интенсивности. Изображение объекта может быть восстановлено компьютером путем обратного преобразования Фурье.
Процесс формирования Фурье- образа объекта с помощью пары соосных зонных пластинок возможно трактовать и с другой точки зрения, рассматривая пару зонных пластинок как интерферометр сдвига.


Действительно, рассмотрим сходящуюся сферическую волну с
центром, имеющим координаты (ξ,
,z0). Проходя
через решетку H,
эта волна в + 1-х порядках дифракции восстановит две волны,
у которых осевые координаты центров
z1 и
z2 определяются
формулой линзы (1), (2), а поперечные координаты
ξ
1 и ξ
2 определяются из
линейных соотношений
 Пусть величины A, z0 и δf связаны соотношением (10). Тогда две восстановленные волны, дифрагируя в свою очередь на решетке H2, в +1-х порядках дифракции дадут волны с координатами (ξ3,z3) и (ξ,z3). Аналогично (21)
Пусть величины A, z0 и δf связаны соотношением (10). Тогда две восстановленные волны, дифрагируя в свою очередь на решетке H2, в +1-х порядках дифракции дадут волны с координатами (ξ3,z3) и (ξ,z3). Аналогично (21)
Учитывая, что Δ“z1, z2, а также что z3 ~ z0, из (22), используя (21), получим
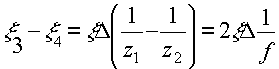 Относительное поперечное смещение центров двух волн с учетом (8) равно
Относительное поперечное смещение центров двух волн с учетом (8) равно
Таким образом оказалось, что центры двукратно дифраги-рованных волн, сходящихся в области наблюдения, имеют взаимное смещение вдоль радиуса, проведенного от оси Z в точку наблюдения, причем величина смещения пропорциональна величине
ξ ύтого радиуса, то есть рассмотренная нами пара соосных зонных пластинок действует как интерферометр радиального сдвига.
Известно [4], что в картине интерференции двух волновых полей на выходе интерферометра радиального сдвига отображается функция пространственной когерентности исходного волнового поля. В соответствии с этим рассматриваемый нами интерферометр радиального сдвига, в принципе, позволяет регистрировать функцию пространственной когерентности волнового поля, формируемого объектом в плоскости наблюдения. Этот вывод, естественно, согласуется с представлением о том, что плоскость наблюдения z = z3 является Фурье плоскостью по отношению к плоскости объекта, и в ней же формируется Фурье- образ от распределения интенсивности по объекту. Действительно, согласно теореме Ван- Циттерта- Цернике, функция пространственной когерентности поля в дальней зоне является Фурье преобразованием от распределения интенсивности по объекту.
В других терминах зарегистрированное в плоскости наблюдения z = z3 распределение интенсивности можно трактовать как Фурье голограмму интенсивности, полученную в излучении с низкой когерентностью.
Таким образом, положенное в основу настоящей работы предположение о том, что эффект Лау позволяет отображать оптические свойства объекта и на его основе могут быть развиты методы оптической обработки информации, нашло в ходе проведенного анализа достаточное обоснование, причем с различных точек зрения.
Для практической реализации методов оптической обработки информации и восстановления изображений на основе эффекта Лау требуется решить некоторые технологические проблемы, что является предметом дальнейшей работы.
Литература
1. Patorski X. // Appl. Opt. 1985. V. 24. N 4. Р. 2448-2453.
2. Власов Н.Г., Маникало В.В., Пресняков Ю.П. Эффект Лау для высокочастотных дифракционных структур и его применение для фотографирования изображений и спектров// Препринт N 3. ВНИИОФИ, МГТУ "Станкин", 1995.
3. Вест Ч. Голографическая интерферометрия. М.:Мир, 1982.
4. Быковский Ю.А., Зарубин А.М., Ларкин А.И. Частично- когерентная голография. Ее свойства и применение// Квантовая электроника. 1986. Т. 13. N 9. С.1770 -1784.

