СТАЦИОНАРНЫЕ И ДИНАМИЧЕСКИЕ СТРУКТУРЫ
В КОЛЬЦЕВОМ ЛАЗЕРЕ С ПРЕОБРАЗОВАНИЕМ ПОЛЯ
В.И. Шмальгаузен, К.В. Прокофьева
кафедра Общей Физики и Волновых Процессов,
Физический факультет МГУ, Москва, Россия
1. Введение
Исследование поперечных пространственных структур в нелинейных системах с оптической обратной связью представляет значительный интерес как с практической так и с теоретической точек зрения. Такой интерес вызван возможностью кодирования информации в поперечной структуре поля и создания таким образом оптического компьютера нового поколения, некоторой модели человеческой ассоциативной памяти [1].
Пространственные структуры, возникающие в пассивном резонаторе с оператором преобразования поля в цепи обратной связи исследовались в [2]. В работе L.A.Lugiato, M.Brambilla, F.Battipede [3] рассматриваются стационарные пространственные структуры, возникающие в поперечном поле лазера.
Идея введения оператора преобразования поля, примененная в [2], может быть использована и для лазерных систем. Мы будем исследовать пространственные структуры в кольцевом однонаправленном лазере, в котором дополнительно введено преобразование поля. В качестве преобразований рассматриваются поворот поперечного сечения поля на некоторый угол и преобразование масштаба.
Экспериментальные исследования пространственных структур, описанные в [3,6-9], были проведены с учетом широко распространенного СО2 лазера. Однако теоретические выкладки выполнялись для двухуровневой модели активной cреды. В данной работе делается попытка рассмотрения пространственных структур в СО2 лазере с учетом дополнительных вращательных уровней молекулы СО2.
Целью работы является рассмотрение стационарных и динамических структур в лазере с оператором преобразования поля, а также исследование влияния вращательных уровней молекулы СО2 на динамику образования пространственных структур.
2. Моды резонатора с преобразованием поля
Рассмотрим устойчивый однонаправленный резонатор (рис.1) из двух сферических и двух плоских зеркал 1, 2, 3, 4. Поместим в него призму 5 и телескоп 6. Обозначим через Ао, Во, Со, Do, элементы волновой матрицы полного обхода.
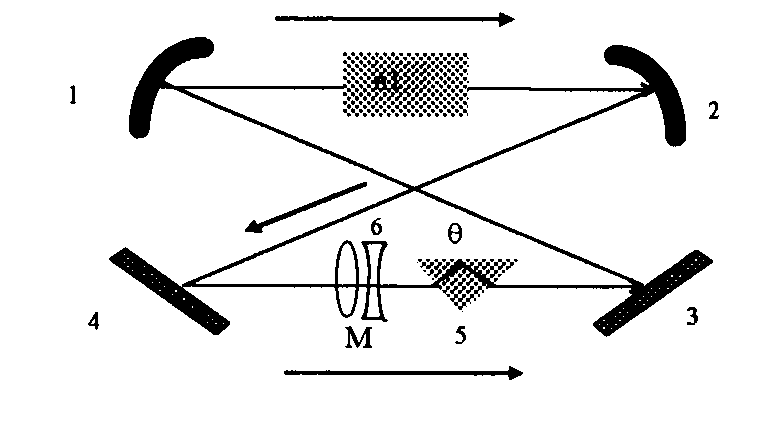
Рис.1. Кольцевой лазер с преобразованием масштаба и поворотом поля. q
- угол поворота, М - преобразование масштаба.
·
Поворот поперечного сечения поля. С помощью призмы при каждом обходе поперечная картина распределения интенсивности поворачивается на угол q
. Такие резонаторы хорошо известны [5], однако не исследовались на предмет образования пространственных динамических структур.
Точное выражение для мод резонатора найдем из интегрального уравнения [4], записанного с учетом поворота поля:
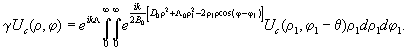 (1)
(1)
Его решение ищем в виде спиральных волн: Uc(r
,j
)
= A(r
) eilj
. Учтя, что множитель 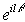 не зависит от переменных интегрирования, получим выражение для частот мод
не зависит от переменных интегрирования, получим выражение для частот мод
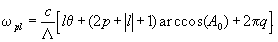 (2)
(2)
Отсюда видно, что при q
¹
0
снимается вырождение по частоте между модами l и -l. Вид поперечного распределения остается таким же. Из (2) следует, что с помощью призмы можно осуществлять плавную перестройку частот мод (с индексами l ¹
0
). Моды Аqpl и Аqp-l имеют теперь различные частоты и их комбинация может рассматриваться как структура, вращающаяся с частотой W
, равной разности частот мод:
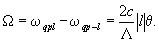 (3)
(3)
·
Изменение масштаба в М раз. Прохождение света через телескоп описывается волновой матрицей
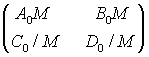 (4)
(4)
что приводит к следующему выражению для частот мод:
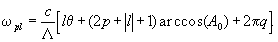 (5)
(5)
При q
¹
0
видно, что для совмещения по частоте различных поперечных мод угол поворота должен быть пропорционален 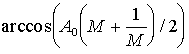 . При М¹
1 значения нужного угла можно просто регулировать изменением коэффициента увеличения в пределах, когда резонатор остается устойчивым.
. При М¹
1 значения нужного угла можно просто регулировать изменением коэффициента увеличения в пределах, когда резонатор остается устойчивым.
3. Пространственные структуры в лазере с преобразованием
поля. Двухуровневая модель cреды.
3.1. Динамические уравнения.
Введение в резонатор активной cреды, являющейся системой двухуровневых атомов, приводит к системе уравнений Максвелла-Блоха [3],
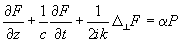 (6)
(6)
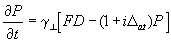 (7)
(7)
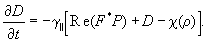 (8)
(8)
Здесь D
^
- поперечный лапласиан, учитывающий пространственные эффекты; a
- коэффициент усиления поля на единицу длины; c
(
r
)
- поперечная конфигурация равновесной инверсии населенности; g
^
, g
|| - поперечная и продольная скорости релаксации; D
at - параметр отстройки частоты генерации w
от атомной частоты перехода w
at : 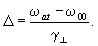
Поле в лазере раскладываем по модам пустого резонатора с поворотом поля:
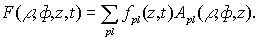 (9)
(9)
Дополним систему уравнений Максвелла-Блоха условием замыкания поля с учетом поворота:
F(z=0,r
,ф,t) = R F(z=L
,r
,ф-q
,t) (10)
Подставляя разложение по модам (9) в (6), учтем ортогональность мод и то, что они удовлетворяют уравнению (6) при a
=0 (в отсутствии cреды). Использовав также тот факт, что моды Аpl являются модами резонатора с поворотом поля, получим уравнения для коэффициентов мод:
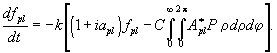 (11)
(11)
Это уравнение по виду полностью совпадает с полученным в [3]. Однако под Аpl здесь понимаются моды резонатора с поворотом поля, которые имеют другие частоты.
3.2. Двухмодовое решение.
В случае возбуждения двух мод из частотно-вырожденного семейства поле записывается в виде:
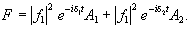 (12)
(12)
здесь d
pl добавка к частоте моды, отличная от нуля если частота моды не совпадает с центром линии усиления.
Коэффициенты мод (l1¹
l2) в адиабатическом приближении вблизи порога удовлетворяют системе уравнений:
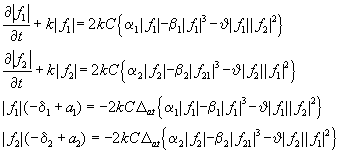 (13)
(13)
Коэффициенты a
i ,
b
i ,
J
равны (i = 1,2):
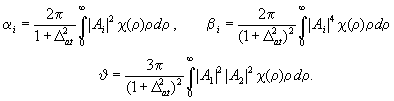 (14)
(14)
Стационарные решения системы (13) имеют вид:
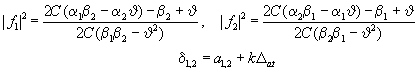 (15)
(15)
Исследовав их на устойчивость, получим условия существования устойчивого двухмодового решения:
2C (a
1b
1 - a
2J
) - b
1 + J
> 0 (16)
2C (a
2b
2 - a
1J
) -b
2 +J
> 0 (17)
b
1b
2 > J
2 (18)
3.3. Особенности системы с поворотом поля.
Существенной особенностью, отличающей систему с повотором поля от рассмотренных в [3], является то, что подбором
угла поворота поля мы можем изменять частоты мод и формировать частично вырожденные семейства из произвольных мод. Эти семейства по составу могут быть отличны от известных.
Частотно-вырожденное семейство из бесконечного числа мод. При угле поворота q
=-arccos (Ao), l>0 частота перестает зависеть от индекса l. Наблюдается вырождение по всем азимутальным индексам, чего не бывает в лазере без поворота поля. В этой связи возникает интересная новая проблема о структуре поперечного распределения поля, образованного бесконечным числом частотно-вырожденных мод. В этом случае возможно развитие различных пространственных неустойчивостей или хаотические режимы.
Взаимодействие мод Ао1 и Ао-1. Картина поперечного распределения интенсивности этих мод демонстрирует вращение с угловой скоростью W
(3). Распределение интенсивности в различные моменты времени показано на рис.2. Исследование на устойчивость такого решения показывает, что оно не является устойчивым ни при каких значениях угла поворота. Однако численный анализ, проведенный за пределами адиабатического приближения, демонстрирует возможность такого режима.
4. Пространственные структуры в СО2 лазере с уточненой
моделью cреды.
Уточнение модели среды при описании СО2 лазера сводится к переходу от идеализации двухуровневой cреды к более сложной модели, учитывающей реальную структуру энергетических уровней молекулы СО2.
Рассмотрим модель, аналогичную исследовавшейся в [10-11]. Вращательные подуровни, относящиеся к одному колебательному уровню объединены в одну группу. Каждая группа состоит из J вращательных подуровней. Генерация происходит на двух выделенных уровнях, которые на рис.4 вынесены из общей группы вращательных подуровней. Фактически такая схема может рассматриваться как четырехуровневая.
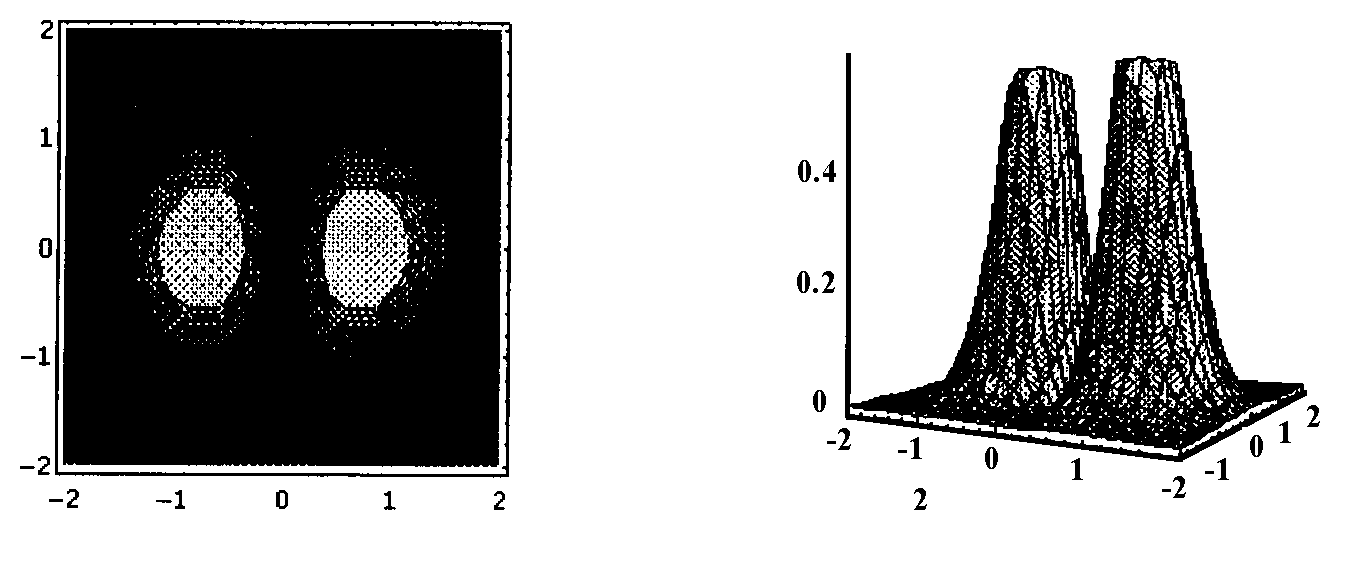
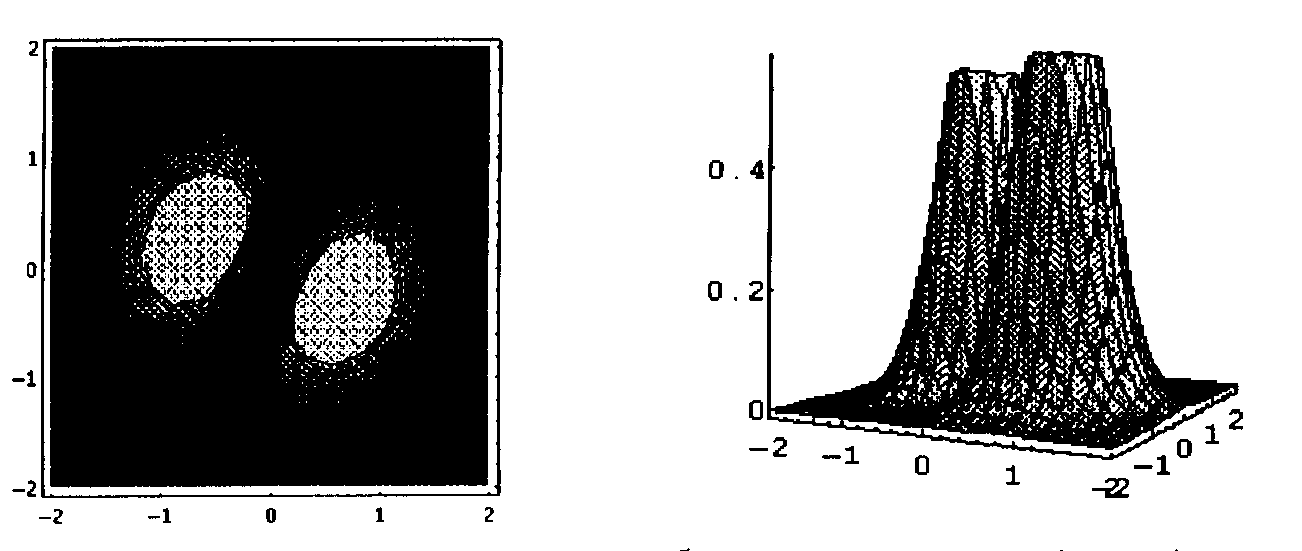
Рис.2. Вращающаяся структура, образованная модами Ао1 и Ао-1. а) момент времени t=0, б) момент времени t=2p
/ 6W
4.1. Динамические уравнения
За пределами плоско-волнового приближения учет вращательных подуровней приводит к увеличению размерности задачи:
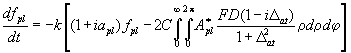 (19)
(19)
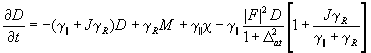 (20)
(20)
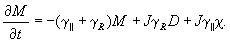 (21)
(21)
здесь М - инверсия населенности между группами вращательных подуровней.
4.1.1. Возможность уменьшения размерности задачи
Как показано в [11], число уравнений, описывающих динамику СО2 лазера в плоско-волновом приближении может быть
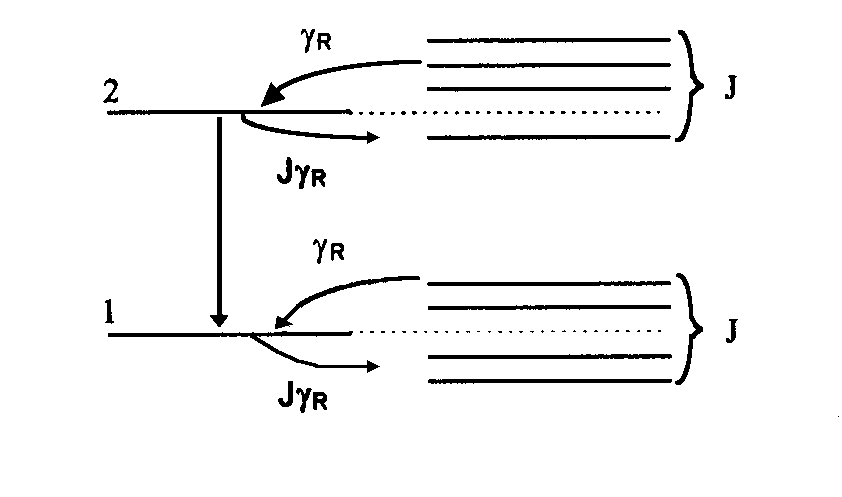
Рис.3. Учет вращательных подуровней молекулы СО2.
уменьшено. Для доказательства этого за пределами плоско-волнового приближения введем малый параметр 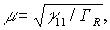 , и сделаем следующую замену переменных:
, и сделаем следующую замену переменных:
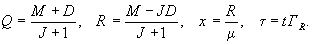 (22)
(22)
Здесь Q имеет смысл средней инверсии населенности. R описывает отклонение от ее среднего значения. Введем также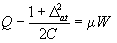 . При этом можно показать, что скорость релаксации х существенно больше скоростей релаксации
. При этом можно показать, что скорость релаксации х существенно больше скоростей релаксации
переменных fpl , W и сделать соответствующее адиабатическое приближение. Возвратившись к старым переменным, получим:
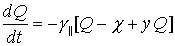 (23)
(23)
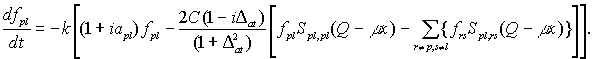 (24)
(24)
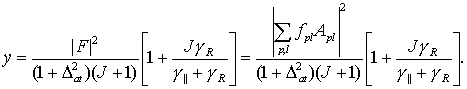 (25)
(25)
Spl,rs - интегральный оператор, введенный для удобства: 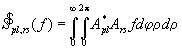 .
.
4.2. Влияние вращательных подуровней молекулы СО2
на образование пространственных структур
Можно показать, что число вращательных подуровней наиболее сильно влияет на интенсивность насыщения, которая возрастает с ростом J:
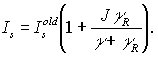
Учет вращательных подуровней приводит к изменению коэффициентов в уравнениях (13). Анализ на устойчивость показывает, что в около пороговой области это не влияет на устойчивость системы.
4.3. Численное моделирование динамики СО2 лазера.
Для исследования процесса развития пространственных структур в лазере нужно рассматривать уравнения (23-25). Рассмотрим динамику двухмодового решения на примере взаимодействия мод Ао1 и Ао-1. Для численного решения использовалось разложение Q по модам и метод Рунге-Кутта 4 порядка с коррекцией шага.
·
Влияние J на динамику мод при q
= 0. Частоты мод при отсутствии угла поворота поля равны. Двухмодовое решение из
этих мод не является устойчивым. Численный анализ показывает, что моды Ао1 и Ао-1 периодически меняются ролями:
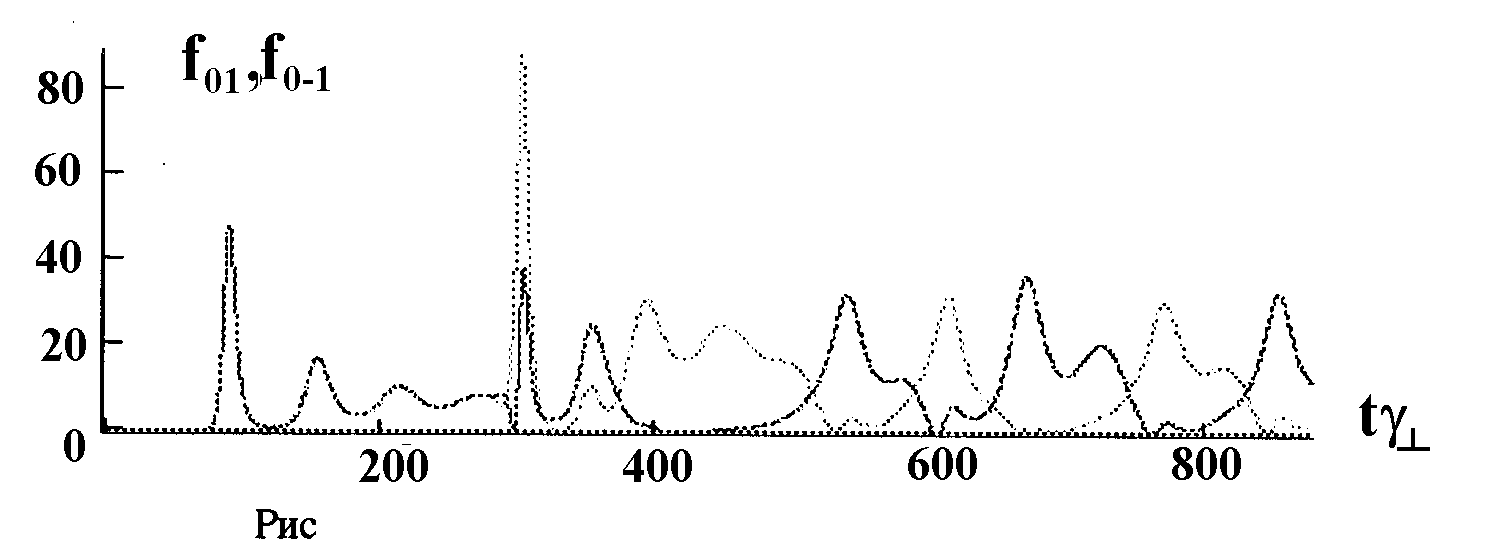
Рис.4. Динамика коэффициентов мод. Параметры q
=0, J=0, C=1.5
При увеличении числа вращательных подуровней одна из мод затухает (рис.5).
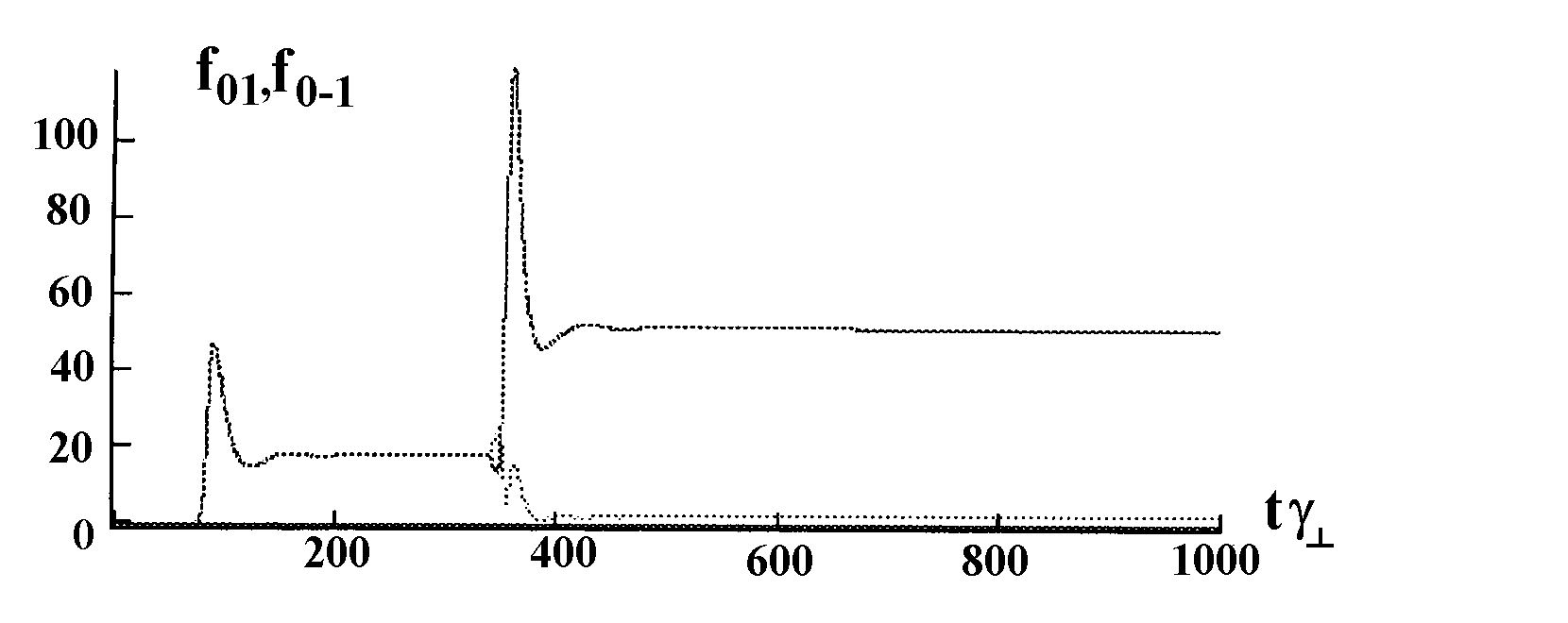
Рис.5. Динамика коэффициентов мод. Параметры q
=0, J=10.
·
Изменение динамики при увеличении угла поворота поля. При q
¹
0
моды находятся на различном расстоянии от центра линии усиления и, следовательно, имеют различные условия для выживания. В результате выживает та мода, которая расположена ближе к частоте атомного перехода.
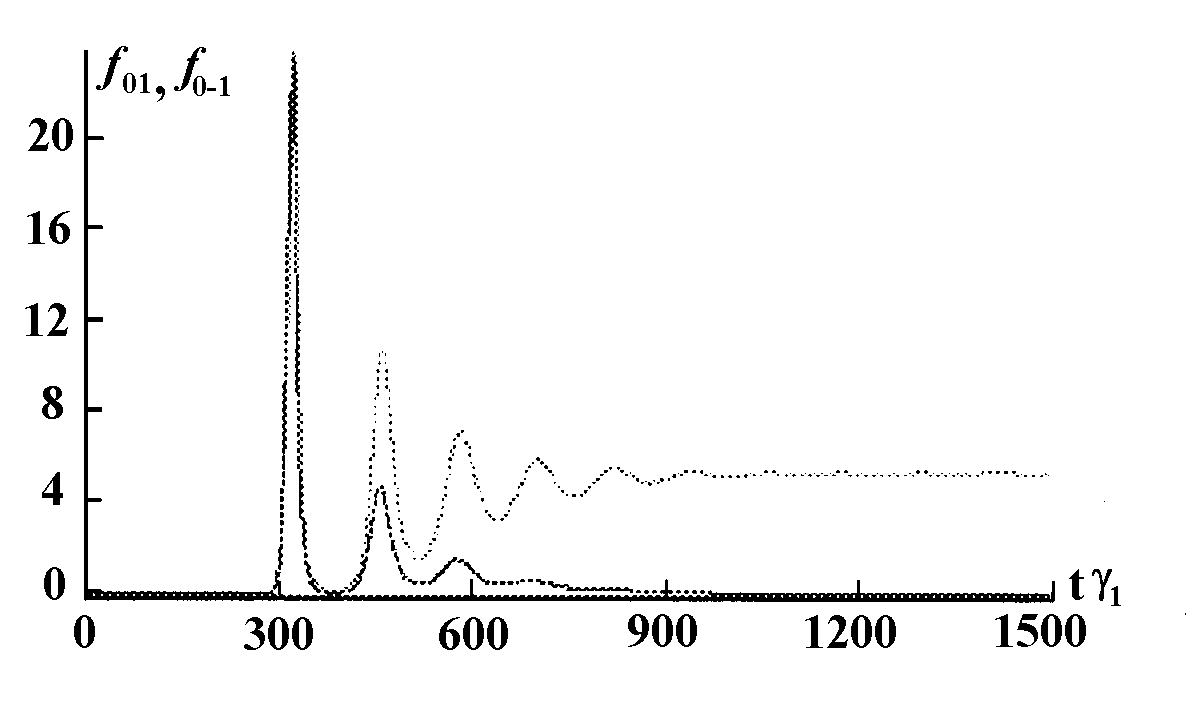
Рис.6. Динамика коэффициентов мод. Серым - мода 01. Параметры: q
=0, J=0, C=1.5. Мода 01 находится ближе к центру линии.
Динамика коэффициентов мод при тех же значениях параметров, но с учетом числа вращательных уровней (J=20) показана
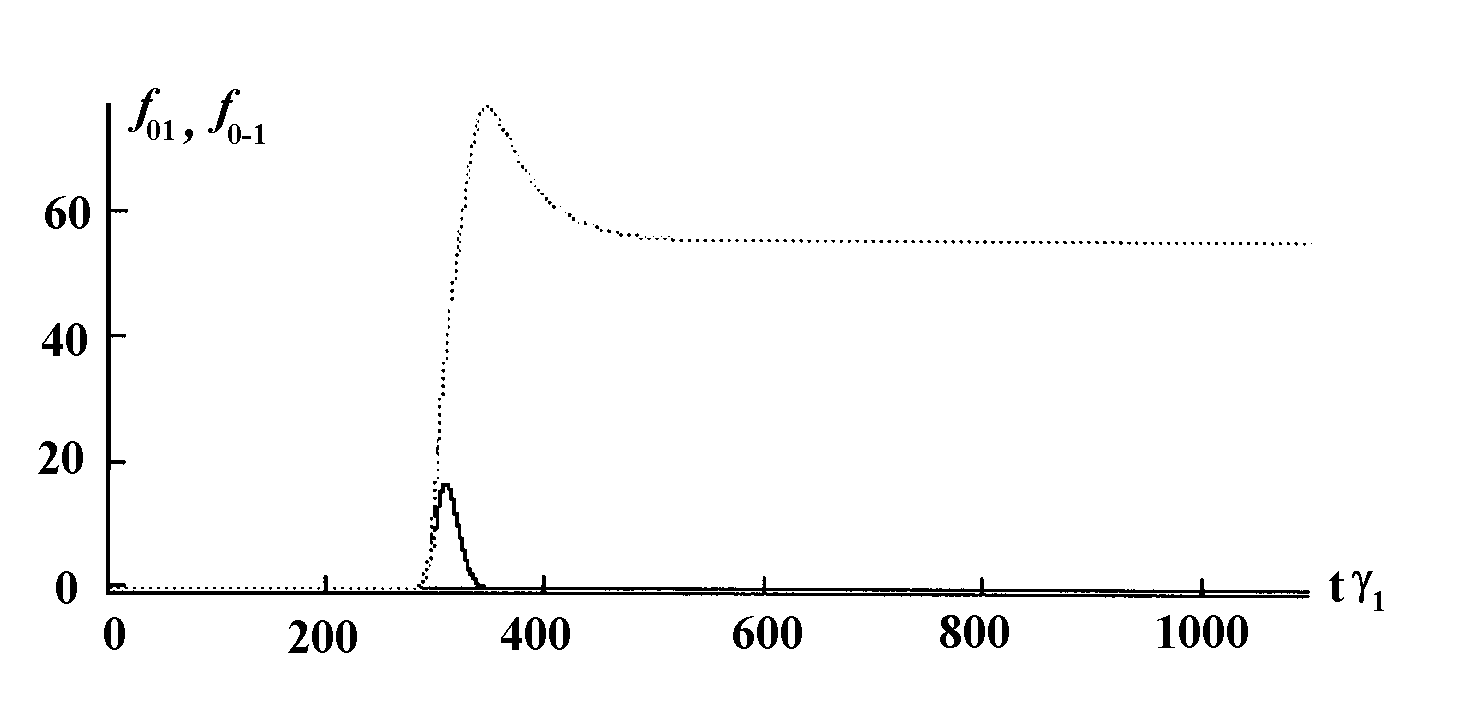
Рис.7. Динамика коэффициентов мод. Серым - мода 01. Параметры: q
=0.1, J=20, C=1.5. Мода 01 находится ближе к центру линии
на рис.7. Число вращательных подуровней увеличило скорость установления стационарного состояния в системе. Характер переходного процесса перестал быть осциллирующим.
Если моды Ао1 и Ао-1 расположены симметрично центра линии усиления, они имеют равные условия в конкурентной борьбе. Обе моды стремятся к одному стационарному состоянию. В поперечной плоскости при этом образуется вращающаяся структура.
5. Обсуждение результатов.
Введение в лазер элемента, осуществляющего поворот поля на некоторый угол приводит к изменению частот мод и, таким образом, предоставляется возможность формирования пространственных структур, отличных от наблюдаемых в обычных лазерах. Поворот поля влияет также на селекци мод, что может быть использовано в эксперименте.
Число вращательных подуровней влияет на скорость установления стационарного значения системы. Режим переключений между модами Ао1 и Ао-1 исчезает при увеличении J.
ЛИТЕРАТУРА
1. Сборник, Новые физические принципы оптической обработки информации.- М.: Наука, 1990.
2. М.А.Воронцов. Ахсеалы - новый класс пространственно-временных неустойчивостей световых полей. Квантовая электроника, (1993), 20, 4.
3. M.Brambilla, F.Battipede, L.A.Lugiato, V.Penna, F.Prati. Transverse laser patterns. 1.Phase singularity crystals. 2.Variational principle for pattern-selection, spatial multistability, laser hydrodynamics // Phys.Rev.A. (1991) 43, 9, 5090.
4. Ю.А.Ананьев. Оптические резонаторы и лазерные пучки. - М.: Наука, 1990, 263 с.
5. И.Г.Кытина, В.М.Нестеренко. Оптический квантовый генератор с повышенной равномерностью поля излучения.// Квантовая электроника (1974) 1, 721.
6. E.T.Arecci, G.Giacomelli, R.P.Ramazzo, Experiment evidence of chaotic itineracy fo spatiotemporal chaos in optics.// Phys.Rev.Lett. (1990) 65, 20, 2531.
7. . E.T.Arecci, G.Giacomelli, R.P.Ramazzo,S. Residori. Vortices and defects statistics in 2D optical chaos.// Phys.Rev.Lett. (1991) 67, 27, 3749
8. J.R.Tredicce. E.J.Quel, A.M.Ghaxxawi, G.Green, Spatio-temporal instabilities in a CO2 laser.// Phys.Rev.Lett. (1989) 62, 11, 1274.
9. D.Hennequim, C.Lepers, E.Louvergneaus, Spatio-temporal dynamics of a weakly multimode CO2 laser.// Opt.Comm.(1992) 93, 5-6, 319.
10. F.A.Hopf, C.K.Fhodes, Influence of vibrational, rotational relaxation on pulse amplification in molecular amplifiers.// Phys.Rev.A (1973) 8, 2, 912.
11. G.L.Oppo, J.R.Tredicce, L.M.Narducci, Dynamical of vibro-rotation CO2 laser transitions in a 2D phase space.// Opt.Comm. (1989), 69, 5, 393.

