Media-security

ОСОБЕННОСТИ ПРИМЕНЕНИЯ ИНТЕРФЕРОМЕТРА

ФАБРИ-ПЕРО В ЗАДАЧАХ КИНОГОЛОГРАФИИ

Ю.Н.Захаров, Е.Г.Сидорова

Нижегородский государственный университет

Нижний Новгород, 603600, пр.Гагарина, 23

В настоящее время интерферометр Фабри-Перо (ИФП) широко используется не только в спектроскопии и квантовой электронике, но и во многих областях, в том числе для формирования опорного пучка в скоростной киноголографии [1]. Причем, в этом случае он освещается широким веерным пучком. Однако, при освещении сильно расходящимся или сильно сходящимся пучком параксиальное приближение, повсеместно принятое для описания работы интерферометра [2-4] не работает даже для идеального ИФП, и известная функция Эри не дает адекватного описания интерференционной картины, тогда как максимальное число киноголограммы определяется отношением расстояния между кольцами в ширине колец.

Проведем анализ процесса формирования интерференционной картины в плоскости за ИФП при освещении точечным источником. Задачу об освещении зеркальных поверхностей ИФП точечным монохроматическим источником с длиной волны l можно свести к задаче о суммировании волн, исходящих от всех изображений этого источника, созданных зеркальными поверхностями ИФП. Таким образом, интерференционную картину в фокальной плоскости линзы, расположенной за ИФП, будем искать как результат сложения волн, идущих от точечных источников, расположенных эквидистантно перед ИФП, начиная с расстояния d и далее через интервал 2h, где h-база ИФП

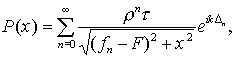
x -расстояние от оптической оси системы до рассматриваемой точки в плоскости наблюдения,

D _n - оптическая длина пути от n-го источника,

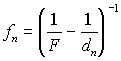- расстояние от линзы до изображения n-го источника, построенного линзой,

d_n - расстояние от n-го источника до линзы,

F - фокусное расстояние линзы,

r , t - энергетические коэффициенты отражения и пропускания зеркальных слоев ИФП.

Оптическая длина пути D n складываются из трех составляющих:

а) от источника до линзы;

б) внутри линзы;

в) от линзы до плоскости наблюдения.

Подставляя каждую из этих составляющих в исходное выражение, получим:

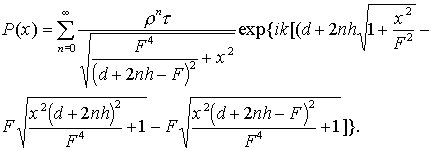
Корни в показателе экспоненты можно разложить в ряды, отбросив слагаемые порядка 10^-6. Тогда,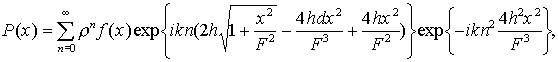

где в функцию f(x) выведены все слагаемые, не содержащие n. Для дальнейших вычислений удобно перейти к интегралу с помощью d -функции:

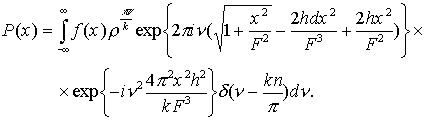
Можно заметить, что интеграл представляет собой преобразование Фурье от произведения функций

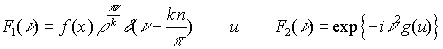
с ядром преобразова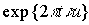ния , где введены дополнительные обозначения:

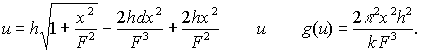
Следовательно, интеграл можно представить в виде свертки преобразований Фурье от каждой из функций F₁(u ) и F₂(u ). Нетрудно видеть, что преобразование Фурье от F₁(u ) имеет вид функции Эри:

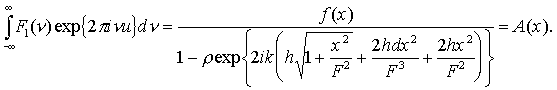
C точностью до постоянных фазовых состояний:

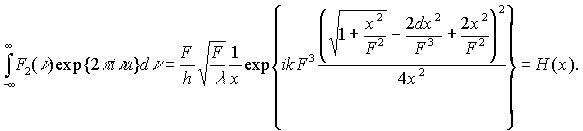
Значит, искомое распределение поля есть свертка известной функции Эри с найденной функцие H(x):

P(x)=A(x)*H(x)

H(x) представляет собой sinc-образную функцию переменной частоты, меняющую скорость осцилляций в зависимости от параметра d (рис.1). Свертка А(х) с Н(х) приводит к искажению формы аппаратного контура ИФП (АК), проявляющемуся, в частности, в уширении колец. Причем, степень этого уширения сильно осциллирует с изменением расходимости освещающей волны.

Таким образом, даже небольшое смещение ИФП относительно центра расходимости (сходимости) освещающей волны может существенно влиять на реальную ширину аппаратного контура, и результат расчета параметров интерференционной картины может быть неверным, если считать АК "классическим" и не учитывать уширение колец вследствие особенностей освещения.

Экспериментальная проверка полученных результатов подтвердила их справедливость. В качестве монохроматического

источника использовался He-Ne лазер. Чтобы получить широкую картину колец [1], излучение было коллимировано. Для обеспечения сильной расходимости пучок фокусировался объктивом вблизи зеркальных поверхностей ИФП. Передвигая объектив вдоль оптической оси, можно было получить и параксиальное освещение. Измерения проводились для ИФП с h=1 мм и h=16 мм. В плоскости наблюдения исследовалась зависимость ширины третьего кольца интерференционной картины от расстояния до "точечного источника".

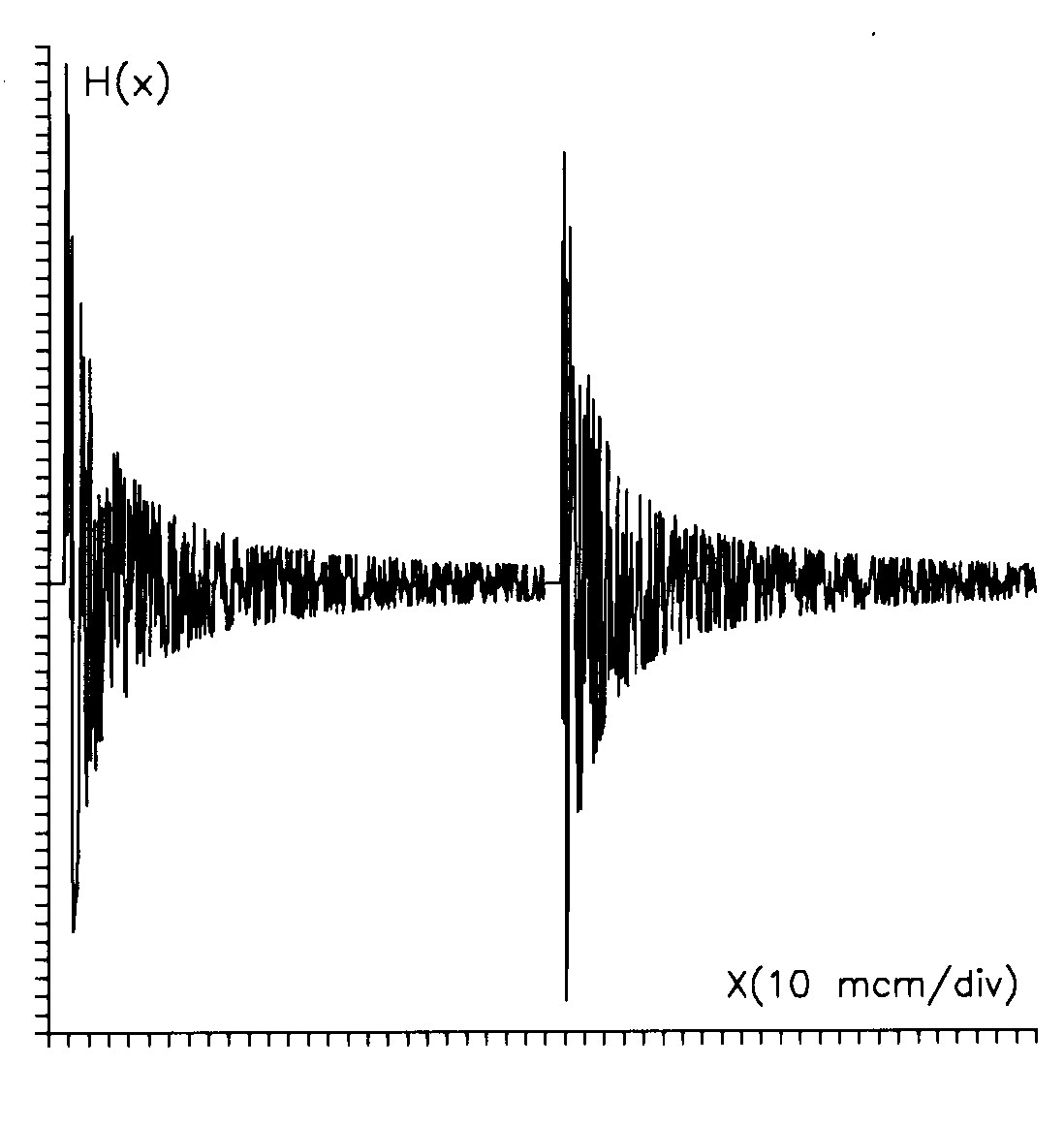
Рис.1. Ядро свертки функции Эри в случае широкого

веерного пучка на входе ИФП для двух значений

радиуса расходимости.

Результаты измерений отражены на рис.2, из которого следует, что ширину АК можно с уверенностью считать "классической" лишь при освещении ИФП слабо расходящимся пучком. При фокусировке излучения вблизи зеркал, ширина АК, как и следует из проведенного анализа, квазипериодически зави-

сит от d, ограничивая предельные возможности голографических схем. Таким образом, при построении и настройке установок, использующих интерферометры Фабри-Перо, нужно располагать микрообъектив, формирующий пучок, на расстояниях, обеспечивающих минимальную ширину АК, что послужит увеличению числа кадров и/или снижению интермодуляционных помех различных кадров одной мультиплексной голограммы.

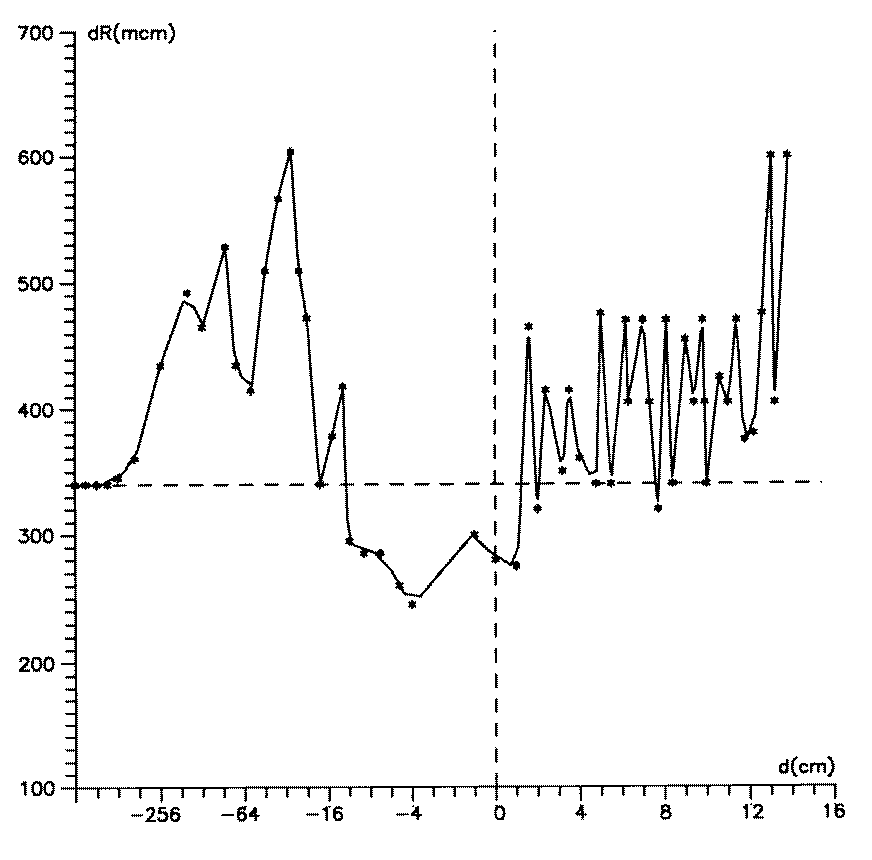
Рис.2. Ширина аппаратного контура ИФП при освещении веерным пучком.

Автор выражает благодарность Савикину А.П. за полезные обсуждения и помощью в проведении эксперимента.

ЛИТЕРАТУРА

1.Захаров Ю.Н., Менсов С.Н. Применение сканирующих интерферометров Фабри-Перо в задачах регистрации быстропротекающих процессов.//ЖТФ.-Т.52, в.5, с.992-995.

2. Борн М., Вольф Э. Основы оптики.- М.: Наука, 1970, 885 с.

3. Cooper V.G. Analisys of Fabry-Perot Interferograms by Means of Their Fourier Transforms.// Applied Optics.-1971.-v.10. №3, pp.525-530.

4. Жиглинский А.Г., Кучинский В.В., Реальный интерферометр Фабри-Перо.-Л.: Машиностроение, 1983, 176 с.